Chủ đề hiện tượng nhiễu xạ ánh sáng: Hiện tượng nhiễu xạ ánh sáng là một khái niệm quan trọng trong vật lý học, giải thích cách ánh sáng tương tác với vật chất và hình thành các mô hình phức tạp. Bài viết này sẽ giúp bạn hiểu rõ hơn về bản chất của nhiễu xạ, các ứng dụng thực tiễn và những hiện tượng thú vị liên quan.
Mục lục
- Hiện Tượng Nhiễu Xạ Ánh Sáng
- Mục Lục Tổng Hợp
- Bài tập 1: Tính góc nhiễu xạ
- Bài tập 2: Xác định kích thước vật cản từ nhiễu xạ
- Bài tập 3: Ứng dụng nhiễu xạ trong thiết kế ánh sáng
- Bài tập 4: Tính đường kính sợi tóc từ nhiễu xạ
- Bài tập 5: Phân tích bức tranh nhiễu xạ trên lưới
- Bài tập 6: Xác định bước sóng ánh sáng qua nhiễu xạ
- Bài tập 7: So sánh nhiễu xạ qua các khe khác nhau
- Bài tập 8: Tính hiệu ứng nhiễu xạ trên một vật liệu mới
- Bài tập 9: Phân tích nhiễu xạ trên các vật liệu có tính chất khác nhau
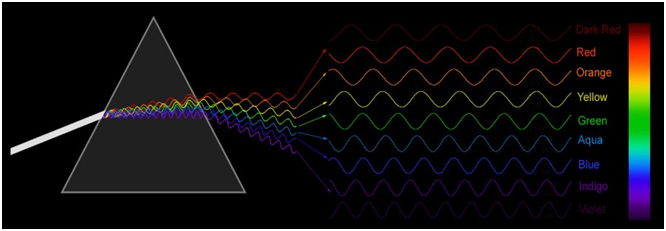
- Bài tập 10: Nhiễu xạ và phân tán màu sắc
- Dạng Bài Tập Về Hiện Tượng Nhiễu Xạ Ánh Sáng
- Bài Tập 1: Tính Toán Vị Trí Các Vân Sáng Trong Thí Nghiệm Young
- Bài Tập 2: Xác Định Góc Nghiêng Cho Vân Sáng Bậc Nhất
- Bài Tập 3: Ứng Dụng Công Thức Fresnel Trong Nhiễu Xạ Qua Khe Hẹp
- Bài Tập 4: Tính Toán Cường Độ Sáng Của Vân Trung Tâm
- Bài Tập 5: So Sánh Vị Trí Các Vân Trong Nhiễu Xạ Qua Khe Kép Và Khe Đơn
- Bài Tập 6: Ứng Dụng Hiện Tượng Nhiễu Xạ Trong Quang Phổ
- Bài Tập 7: Tính Bước Sóng Ánh Sáng Qua Thí Nghiệm Nhiễu Xạ
- Bài Tập 8: Phân Tích Hiện Tượng Nhiễu Xạ Qua Mạng Tinh Thể
- Bài Tập 9: Xác Định Điều Kiện Giao Thoa Tăng Cường Và Triệt Tiêu
- Bài Tập 10: Tính Cường Độ Sáng Tại Một Điểm Bất Kỳ Trên Màn Quan Sát
Hiện Tượng Nhiễu Xạ Ánh Sáng
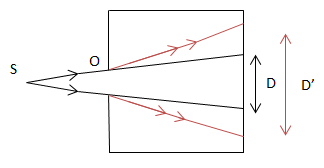
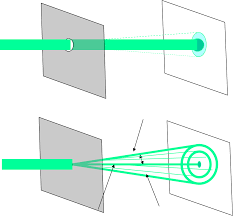
Hiện tượng nhiễu xạ ánh sáng là một trong những minh chứng quan trọng cho tính chất sóng của ánh sáng. Đây là hiện tượng ánh sáng bị bẻ cong khi đi qua các khe hẹp hoặc gặp các vật cản có kích thước nhỏ hơn bước sóng ánh sáng. Trong quá trình này, ánh sáng sẽ lan tỏa và tạo ra các vân sáng, tối xen kẽ nhau trên màn quan sát, gọi là các vân nhiễu xạ.
Nguyên lý Huygens
Nguyên lý Huygens giải thích rằng mỗi điểm trên một mặt sóng khi được ánh sáng chiếu tới sẽ trở thành một nguồn sáng thứ cấp, phát ra sóng cầu truyền về phía trước. Khi các sóng này gặp nhau, chúng sẽ giao thoa và tạo thành các vùng sáng, tối trên màn quan sát. Hiện tượng nhiễu xạ là một ứng dụng điển hình của nguyên lý này.
Thí Nghiệm Nhiễu Xạ
Để quan sát hiện tượng nhiễu xạ, ta thực hiện thí nghiệm chiếu ánh sáng qua khe hẹp hoặc các vật cản nhỏ. Kết quả là ta sẽ thấy các vân sáng tối xen kẽ nhau trên màn hứng, chứng minh rằng ánh sáng có tính chất sóng.
- Với khe chiếu lớn: Ánh sáng truyền thẳng, tạo ra vệt sáng đơn giản.
- Với khe chiếu nhỏ: Các vân sáng, tối xuất hiện rõ rệt do hiện tượng nhiễu xạ.
Công Thức Tính Toán
Các vân nhiễu xạ được hình thành tại các vị trí mà các sóng ánh sáng từ các khe giao thoa với nhau. Vị trí của các vân sáng có thể được tính toán bằng công thức:
\[d \sin \theta = k \lambda\]
Trong đó:
- \(d\) là khoảng cách giữa các khe.
- \(\theta\) là góc tạo bởi vân sáng với trục chính.
- \(\lambda\) là bước sóng ánh sáng.
- \(k\) là bậc của vân sáng (với \(k = 0, \pm 1, \pm 2, ...\)).
Ứng Dụng của Hiện Tượng Nhiễu Xạ
Hiện tượng nhiễu xạ ánh sáng có nhiều ứng dụng trong khoa học và công nghệ:
- Trong phân tích quang học: Sử dụng nhiễu xạ để phân tích cấu trúc của các vật liệu, đặc biệt là trong quang phổ học.
- Trong công nghệ laser: Nhiễu xạ giúp tăng cường khả năng điều khiển và định hướng chùm tia laser.
- Trong y học: Nhiễu xạ tia X giúp xác định cấu trúc của các protein và DNA, hỗ trợ trong việc phát triển các loại thuốc mới.
Tổng Kết
Hiện tượng nhiễu xạ ánh sáng là minh chứng rõ ràng cho tính chất sóng của ánh sáng, đồng thời mở ra nhiều ứng dụng quan trọng trong khoa học và công nghệ hiện đại.

.png)
Mục Lục Tổng Hợp
1. Hiện tượng nhiễu xạ ánh sáng là gì?
2. Nguyên lý cơ bản của nhiễu xạ ánh sáng
3. Các loại nhiễu xạ: khe hẹp, lưới nhiễu xạ, nhiễu xạ trên sợi tóc
4. Công thức tính nhiễu xạ ánh sáng
\( \frac{\lambda}{d} = \frac{a_1/2}{L} \)
\( b\sin\varphi_k = \pm k\lambda \)
5. Ứng dụng của nhiễu xạ ánh sáng trong đời sống và công nghệ
Nhiếp ảnh và nghệ thuật
Thiết kế ánh sáng
Mô phỏng vật lý
Chẩn đoán y tế
Kỹ thuật quang học
6. Thí nghiệm nhiễu xạ ánh sáng
Nhiễu xạ trên khe hẹp
Nhiễu xạ trên lưới nhiễu xạ
Nhiễu xạ trên sợi tóc
7. Các yếu tố ảnh hưởng đến hiện tượng nhiễu xạ
8. Bài tập ví dụ về nhiễu xạ ánh sáng
Bài tập 1: Tính góc nhiễu xạ
Bài tập 3: Ứng dụng nhiễu xạ trong thiết kế ánh sáng
XEM THÊM:
Bài tập 5: Phân tích bức tranh nhiễu xạ trên lưới

Bài tập 6: Xác định bước sóng ánh sáng qua nhiễu xạ
Bài tập 8: Tính hiệu ứng nhiễu xạ trên một vật liệu mới
Bài tập 9: Phân tích nhiễu xạ trên các vật liệu có tính chất khác nhau
Bài tập 10: Nhiễu xạ và phân tán màu sắc
Dạng Bài Tập Về Hiện Tượng Nhiễu Xạ Ánh Sáng
Dưới đây là một số dạng bài tập thường gặp liên quan đến hiện tượng nhiễu xạ ánh sáng. Các bài tập được trình bày chi tiết, kèm theo hướng dẫn giải để giúp bạn hiểu rõ hơn về hiện tượng này.
-
Bài tập 1: Tính góc nhiễu xạ
Cho bước sóng ánh sáng \(\lambda = 600 \, \text{nm}\) và khe hẹp có bề rộng \(d = 0.1 \, \text{mm}\). Tính góc nhiễu xạ đầu tiên (\(\theta\)) khi hiện tượng nhiễu xạ xảy ra.
Gợi ý: Sử dụng công thức \(\sin\theta = \frac{k\lambda}{d}\), với \(k = 1\).
-
Bài tập 2: Xác định kích thước vật cản từ nhiễu xạ
Ánh sáng có bước sóng \(500 \, \text{nm}\) chiếu tới một vật cản có bề rộng \(a\). Nếu khoảng cách giữa các vân nhiễu xạ trên màn ảnh là \(y = 1 \, \text{mm}\), hãy xác định kích thước của vật cản.
Gợi ý: Sử dụng công thức nhiễu xạ đơn giản: \(\frac{\lambda}{a} = \frac{y}{L}\), với \(L\) là khoảng cách từ vật cản đến màn ảnh.
-
Bài tập 3: Ứng dụng nhiễu xạ trong thiết kế ánh sáng
Một nhà thiết kế ánh sáng muốn tạo ra hiệu ứng nhiễu xạ rõ nét trong một không gian triển lãm. Ánh sáng có bước sóng \(450 \, \text{nm}\) được sử dụng. Tính kích thước các khe cần thiết để tạo ra các vân sáng cách nhau \(2 \, \text{cm}\) trên màn ảnh đặt cách nguồn sáng \(2 \, \text{m}\).
-
Bài tập 4: Tính đường kính sợi tóc từ nhiễu xạ
Một chùm tia laser có bước sóng \(632.8 \, \text{nm}\) chiếu qua một sợi tóc tạo ra các vân nhiễu xạ. Nếu khoảng cách giữa hai vân sáng liên tiếp là \(1.2 \, \text{mm}\) trên màn ảnh cách sợi tóc \(1 \, \text{m}\), hãy tính đường kính của sợi tóc.
Gợi ý: Sử dụng công thức tương tự bài tập 2.
-
Bài tập 5: Phân tích bức tranh nhiễu xạ trên lưới
Một bức tranh nhiễu xạ được tạo ra bởi lưới nhiễu xạ có số đường là \(500 \, \text{đường}/\text{mm}\). Bước sóng ánh sáng chiếu tới là \(700 \, \text{nm}\). Hãy tính khoảng cách giữa các vân sáng trên màn ảnh cách lưới \(1.5 \, \text{m}\).
-
Bài tập 6: Xác định bước sóng ánh sáng qua nhiễu xạ
Trong một thí nghiệm, ánh sáng có bước sóng chưa biết được chiếu qua một khe hẹp có bề rộng \(0.2 \, \text{mm}\). Khoảng cách giữa hai vân tối liên tiếp trên màn ảnh là \(4 \, \text{mm}\). Tính bước sóng của ánh sáng.
-
Bài tập 7: So sánh nhiễu xạ qua các khe khác nhau
Hai khe hẹp có bề rộng khác nhau được chiếu bởi cùng một nguồn sáng đơn sắc. Nếu khe thứ nhất tạo ra góc nhiễu xạ đầu tiên là \(5^\circ\), thì góc nhiễu xạ đầu tiên của khe thứ hai sẽ là bao nhiêu nếu bề rộng của khe thứ hai gấp đôi khe thứ nhất?
-
Bài tập 8: Tính hiệu ứng nhiễu xạ trên một vật liệu mới
Một vật liệu mới có chỉ số khúc xạ \(n = 1.5\) được sử dụng trong một thí nghiệm nhiễu xạ. Tính khoảng cách giữa các vân sáng khi ánh sáng có bước sóng \(600 \, \text{nm}\) chiếu qua một khe hẹp \(d = 0.1 \, \text{mm}\), với màn ảnh cách nguồn sáng \(1 \, \text{m}\).
-
Bài tập 9: Phân tích nhiễu xạ trên các vật liệu có tính chất khác nhau
So sánh hiện tượng nhiễu xạ xảy ra trên một vật liệu có chỉ số khúc xạ cao với một vật liệu có chỉ số khúc xạ thấp khi cùng chiếu ánh sáng đơn sắc qua một khe hẹp.
-
Bài tập 10: Nhiễu xạ và phân tán màu sắc
Trong một thí nghiệm, ánh sáng trắng được chiếu qua một lưới nhiễu xạ. Giải thích hiện tượng phân tán màu sắc xuất hiện trên màn ảnh.
Bài Tập 1: Tính Toán Vị Trí Các Vân Sáng Trong Thí Nghiệm Young
Trong thí nghiệm Young về nhiễu xạ ánh sáng, ta có thể tính toán vị trí các vân sáng trên màn dựa vào công thức đơn giản. Dưới đây là các bước chi tiết để giải quyết bài tập này.
-
Bước 1: Xác định các giá trị cần thiết
Cho biết khoảng cách giữa hai khe \(d\), bước sóng ánh sáng sử dụng \(\lambda\), và khoảng cách từ khe đến màn \(L\). Các giá trị này sẽ được sử dụng để tính vị trí vân sáng.
-
Bước 2: Sử dụng công thức tính vị trí các vân sáng
Vị trí của vân sáng thứ \(n\) trên màn hình được tính bằng công thức:
\[ y_n = \frac{n\lambda L}{d} \]Trong đó:
- \(y_n\) là khoảng cách từ vân trung tâm đến vân sáng thứ \(n\).
- \(\lambda\) là bước sóng của ánh sáng.
- \(L\) là khoảng cách từ hai khe đến màn hình.
- \(d\) là khoảng cách giữa hai khe.
- \(n\) là số thứ tự của vân sáng (n = 0 là vân trung tâm).
-
Bước 3: Thực hiện tính toán
Thay các giá trị đã cho vào công thức trên để tính khoảng cách \(y_n\). Hãy chắc chắn rằng các đơn vị đo lường nhất quán để tránh sai sót.
-
Bước 4: Phân tích kết quả
Sau khi tính toán, bạn sẽ xác định được vị trí của các vân sáng trên màn. Kết quả này giúp bạn hiểu rõ hơn về sự phân bố của ánh sáng trong thí nghiệm nhiễu xạ.
Bài Tập 2: Xác Định Góc Nghiêng Cho Vân Sáng Bậc Nhất
Trong bài tập này, chúng ta sẽ xác định góc nghiêng cho vân sáng bậc nhất trong thí nghiệm nhiễu xạ ánh sáng. Dưới đây là các bước cụ thể để giải bài tập này một cách chi tiết và chính xác.
-
Bước 1: Xác định các thông số ban đầu
Cho biết khoảng cách giữa hai khe \(d\), bước sóng ánh sáng \(\lambda\), và khoảng cách từ khe đến màn \(L\). Các thông số này là cơ sở để tính toán góc nghiêng.
-
Bước 2: Áp dụng công thức tính góc nghiêng
Góc nghiêng \(\theta_1\) của vân sáng bậc nhất có thể được tính bằng công thức:
\[ \sin\theta_1 = \frac{\lambda}{d} \]Trong đó:
- \(\theta_1\) là góc nghiêng của vân sáng bậc nhất.
- \(\lambda\) là bước sóng của ánh sáng.
- \(d\) là khoảng cách giữa hai khe.
-
Bước 3: Tính toán và tìm góc nghiêng
Sau khi thay các giá trị cụ thể vào công thức, sử dụng hàm sin nghịch đảo để tính góc nghiêng \(\theta_1\). Đảm bảo rằng đơn vị góc là radian hoặc độ, tùy vào yêu cầu của bài toán.
-
Bước 4: Phân tích và kiểm tra kết quả
Sau khi tính toán, phân tích kết quả để đảm bảo rằng góc nghiêng xác định là hợp lý và phản ánh đúng hiện tượng nhiễu xạ ánh sáng trong thí nghiệm.
Bài Tập 3: Ứng Dụng Công Thức Fresnel Trong Nhiễu Xạ Qua Khe Hẹp
Trong bài tập này, chúng ta sẽ áp dụng công thức Fresnel để phân tích hiện tượng nhiễu xạ qua khe hẹp. Các bước dưới đây sẽ hướng dẫn chi tiết cách giải quyết bài tập một cách khoa học và hiệu quả.
-
Bước 1: Xác định các thông số cơ bản
Cho biết chiều rộng khe hẹp \(a\), bước sóng ánh sáng \(\lambda\), và khoảng cách từ khe đến màn \(L\). Những giá trị này cần được xác định trước khi áp dụng công thức Fresnel.
-
Bước 2: Áp dụng công thức Fresnel
Biểu thức tính cường độ sáng \(I(x)\) tại điểm \(x\) trên màn có thể được mô tả bằng công thức Fresnel như sau:
\[ I(x) = I_0 \cdot \left(\frac{\sin(\beta/2)}{\beta/2}\right)^2 \]Trong đó:
- \(\beta = \frac{2\pi a x}{\lambda L}\) là tham số liên quan đến độ rộng khe và vị trí trên màn.
- \(I_0\) là cường độ sáng tại tâm của vân sáng chính.
-
Bước 3: Tính toán cường độ sáng tại các vị trí cụ thể
Sau khi xác định các tham số, tiến hành tính toán cường độ sáng tại các vị trí khác nhau trên màn, đặc biệt là tại các vân tối và vân sáng.
-
Bước 4: So sánh và đối chiếu kết quả
So sánh kết quả tính toán với thực nghiệm hoặc với các bài tập tương tự để kiểm tra độ chính xác của quá trình giải.

Bài Tập 4: Tính Toán Cường Độ Sáng Của Vân Trung Tâm
Trong bài tập này, chúng ta sẽ tính toán cường độ sáng của vân trung tâm trong thí nghiệm nhiễu xạ ánh sáng qua một khe hẹp. Các bước dưới đây sẽ hướng dẫn chi tiết cách thực hiện phép tính này một cách chính xác.
-
Bước 1: Xác định thông số cơ bản
Đầu tiên, cần xác định bước sóng ánh sáng \(\lambda\), độ rộng khe \(a\), và khoảng cách từ khe đến màn \(L\).
-
Bước 2: Tính toán tham số \(\beta\)
Tham số \(\beta\) được tính theo công thức:
\[ \beta = \frac{2\pi a \cdot x}{\lambda \cdot L} \]Với \(x = 0\) tại vị trí trung tâm, giá trị của \(\beta\) bằng 0.
-
Bước 3: Áp dụng công thức tính cường độ sáng \(I\)
Cường độ sáng tại vân trung tâm được tính theo công thức:
\[ I(0) = I_0 \cdot \left(\frac{\sin(\beta/2)}{\beta/2}\right)^2 \]Với \(\beta = 0\), cường độ sáng \(I(0)\) đạt giá trị lớn nhất, bằng \(I_0\).
-
Bước 4: So sánh với các vân khác
So sánh cường độ sáng tại vân trung tâm với các vân khác để thấy được sự khác biệt rõ ràng về cường độ sáng.
Bài Tập 5: So Sánh Vị Trí Các Vân Trong Nhiễu Xạ Qua Khe Kép Và Khe Đơn
Trong bài tập này, chúng ta sẽ so sánh vị trí các vân sáng và vân tối xuất hiện trong hiện tượng nhiễu xạ qua khe đơn và khe kép. Đây là một phần quan trọng trong việc hiểu sâu hơn về bản chất của ánh sáng và sự tương tác của nó với các vật cản.
1. Nhiễu Xạ Qua Khe Đơn
Trong nhiễu xạ qua khe đơn, ánh sáng đi qua một khe hẹp sẽ bị bẻ cong và tạo ra các vân sáng và vân tối trên màn quan sát. Vị trí các vân này được xác định bởi công thức:
Trong đó:
- \(a\) là độ rộng của khe đơn.
- \(\theta\) là góc lệch so với trục trung tâm (góc nhiễu xạ).
- \(m\) là bậc của vân (m = 0, ±1, ±2,...).
- \(\lambda\) là bước sóng của ánh sáng.
Các vân sáng xuất hiện tại các vị trí góc \(\theta\) thỏa mãn công thức trên với \(m = 0, \pm 1, \pm 2, \ldots\), trong khi các vân tối xuất hiện khi \(m\) là một số nửa nguyên (ví dụ, \(m = \pm \frac{1}{2}, \pm \frac{3}{2}, \ldots\)).
2. Nhiễu Xạ Qua Khe Kép
Trong nhiễu xạ qua khe kép, ánh sáng đi qua hai khe hẹp song song với nhau. Khi hai sóng ánh sáng từ hai khe này giao thoa, chúng tạo ra một mô hình vân sáng và vân tối trên màn, với các vị trí được xác định bởi công thức:
Trong đó:
- \(d\) là khoảng cách giữa hai khe.
- \(\theta\) là góc lệch so với trục trung tâm (góc giao thoa).
- \(n\) là bậc của vân giao thoa (n = 0, ±1, ±2,...).
- \(\lambda\) là bước sóng của ánh sáng.
Vị trí các vân sáng được xác định khi \(d \sin(\theta) = n\lambda\) và các vân tối khi \(d \sin(\theta) = (n + \frac{1}{2})\lambda\).
3. So Sánh Vị Trí Các Vân
Khi so sánh nhiễu xạ qua khe đơn và khe kép, chúng ta nhận thấy một số điểm khác biệt và tương đồng quan trọng:
- Vị trí các vân sáng: Ở cả khe đơn và khe kép, các vân sáng xuất hiện tại các vị trí góc \(\theta\) tương ứng với bội số của bước sóng \(\lambda\). Tuy nhiên, trong khe kép, vị trí các vân sáng rõ ràng và phân bố đều hơn so với khe đơn.
- Số lượng và cường độ của các vân: Trong nhiễu xạ qua khe kép, có nhiều vân sáng và tối hơn, do sự giao thoa của hai nguồn ánh sáng. Cường độ các vân sáng trong nhiễu xạ khe kép cũng mạnh hơn do sự kết hợp của hai sóng ánh sáng.
- Độ rộng của các vân: Vân sáng và tối trong nhiễu xạ qua khe đơn có độ rộng lớn hơn so với khe kép. Điều này là do sự phân tán ánh sáng mạnh hơn khi chỉ có một khe.
Bài tập này giúp bạn hiểu rõ hơn về hiện tượng nhiễu xạ và giao thoa của ánh sáng khi qua các loại khe khác nhau, từ đó có thể áp dụng vào các tình huống thực tế trong quang học và khoa học vật lý.
Bài Tập 6: Ứng Dụng Hiện Tượng Nhiễu Xạ Trong Quang Phổ
Hiện tượng nhiễu xạ ánh sáng có nhiều ứng dụng quan trọng trong quang học, đặc biệt là trong việc phân tích quang phổ. Quang phổ kế là một thiết bị sử dụng nguyên lý nhiễu xạ để phân tích và xác định thành phần của ánh sáng qua sự phân tách của các bước sóng khác nhau. Dưới đây là chi tiết cách ứng dụng hiện tượng nhiễu xạ trong quang phổ.
1. Nguyên lý hoạt động của quang phổ kế dựa trên nhiễu xạ
Quang phổ kế sử dụng một cách tử nhiễu xạ (grating) để phân tách ánh sáng thành các thành phần bước sóng của nó. Khi một chùm ánh sáng trắng đi qua cách tử nhiễu xạ, nó sẽ bị tán sắc thành các bước sóng khác nhau tạo thành một phổ liên tục. Vị trí và cường độ của các bước sóng được xác định dựa trên công thức:
Trong đó:
- \(d\) là khoảng cách giữa các khe của cách tử nhiễu xạ.
- \(\theta\) là góc nhiễu xạ tương ứng với mỗi bước sóng.
- \(m\) là bậc của vân (m = 0, ±1, ±2,...).
- \(\lambda\) là bước sóng của ánh sáng.
Ánh sáng với các bước sóng khác nhau sẽ tạo ra các góc nhiễu xạ khác nhau, dẫn đến sự phân tách rõ ràng của các bước sóng này trên màn quan sát.
2. Ứng dụng trong phân tích hóa học và vật lý
Hiện tượng nhiễu xạ trong quang phổ được sử dụng rộng rãi trong phân tích hóa học và vật lý để xác định thành phần của các chất. Bằng cách đo cường độ và vị trí của các vân sáng tối trong phổ thu được, người ta có thể xác định thành phần hóa học và cấu trúc của mẫu cần phân tích.
Ví dụ, trong các nghiên cứu vật lý và thiên văn học, quang phổ kế được sử dụng để phân tích ánh sáng từ các ngôi sao và hành tinh, từ đó xác định được các nguyên tố hóa học hiện diện trong các thiên thể này.
3. Phân tích và nhận dạng chất bằng quang phổ nhiễu xạ
Trong quá trình phân tích, mẫu vật được chiếu sáng bằng một nguồn ánh sáng đơn sắc hoặc đa sắc. Ánh sáng sau khi tương tác với mẫu sẽ được dẫn qua cách tử nhiễu xạ. Các bước sóng khác nhau sẽ bị nhiễu xạ ở các góc khác nhau, cho phép chúng ta quan sát và ghi lại quang phổ của mẫu. Điều này rất hữu ích trong việc nhận dạng chất liệu, xác định nồng độ, và nghiên cứu tính chất vật lý của mẫu.
4. Các bước thực hiện phân tích quang phổ nhiễu xạ
- Chuẩn bị mẫu: Đặt mẫu cần phân tích trên bàn đo hoặc trong buồng mẫu của quang phổ kế.
- Chiếu sáng mẫu: Sử dụng nguồn sáng (laser hoặc ánh sáng trắng) để chiếu vào mẫu. Đảm bảo nguồn sáng đủ mạnh và ổn định.
- Thu thập quang phổ: Ánh sáng sau khi đi qua mẫu sẽ bị tán sắc bởi cách tử nhiễu xạ, tạo thành quang phổ trên màn quan sát hoặc cảm biến.
- Phân tích dữ liệu: Sử dụng phần mềm chuyên dụng để phân tích các vân sáng, vân tối và cường độ của chúng để xác định các thành phần hóa học và tính chất vật lý của mẫu.
Bài tập này giúp bạn hiểu rõ hơn về ứng dụng của hiện tượng nhiễu xạ trong quang phổ học, từ đó có thể áp dụng trong nghiên cứu khoa học và phân tích hóa học hiện đại.

Bài Tập 7: Tính Bước Sóng Ánh Sáng Qua Thí Nghiệm Nhiễu Xạ
Trong bài tập này, chúng ta sẽ thực hiện các bước tính toán bước sóng của ánh sáng thông qua thí nghiệm nhiễu xạ khe đơn hoặc khe kép. Thí nghiệm này giúp chúng ta hiểu rõ hơn về bản chất của ánh sáng và cách nó tương tác với các vật cản.
1. Thí nghiệm nhiễu xạ khe đơn
Trong thí nghiệm nhiễu xạ qua khe đơn, ánh sáng đi qua một khe hẹp và tạo ra các vân sáng và vân tối trên màn quan sát. Vị trí của các vân sáng có thể được xác định bằng công thức:
Trong đó:
- \(a\) là độ rộng của khe đơn.
- \(\theta\) là góc lệch từ vân trung tâm đến vân sáng thứ \(m\).
- \(m\) là số bậc của vân sáng (m = ±1, ±2,...).
- \(\lambda\) là bước sóng của ánh sáng.
Để tính bước sóng \(\lambda\), chúng ta cần xác định các giá trị của \(a\), \(\theta\), và \(m\). Thông thường, \(\theta\) có thể được đo bằng cách xác định khoảng cách từ khe đến màn quan sát (L) và khoảng cách từ vân trung tâm đến vân sáng thứ \(m\) (y). Sau đó, góc \(\theta\) được tính bằng công thức:
Sau khi có được giá trị \(\sin(\theta)\), bước sóng \(\lambda\) được tính bằng:
2. Thí nghiệm nhiễu xạ khe kép
Trong thí nghiệm nhiễu xạ khe kép, ánh sáng đi qua hai khe hẹp song song và tạo ra các vân giao thoa trên màn quan sát. Vị trí của các vân sáng có thể được xác định bằng công thức:
Trong đó:
- \(d\) là khoảng cách giữa hai khe.
- \(\theta\) là góc lệch từ vân trung tâm đến vân sáng thứ \(n\).
- \(n\) là số bậc của vân sáng (n = 0, ±1, ±2,...).
- \(\lambda\) là bước sóng của ánh sáng.
Tương tự như với khe đơn, \(\theta\) có thể được xác định từ các giá trị đo lường thực tế như khoảng cách từ khe đến màn quan sát (L) và khoảng cách từ vân trung tâm đến vân sáng thứ \(n\) (y). Khi biết giá trị \(\sin(\theta)\), bước sóng \(\lambda\) được tính bằng:
3. Các bước thực hiện thí nghiệm để tính bước sóng
- Chuẩn bị thí nghiệm: Sử dụng một nguồn sáng đơn sắc (như laser), một khe đơn hoặc khe kép, và một màn quan sát để hiển thị các vân nhiễu xạ.
- Đo khoảng cách: Đo khoảng cách từ khe đến màn quan sát (L) và khoảng cách từ vân trung tâm đến các vân sáng thứ \(m\) hoặc \(n\) (y).
- Tính góc nhiễu xạ: Tính giá trị của \(\sin(\theta) = \frac{y}{L}\) để xác định góc nhiễu xạ.
- Tính bước sóng: Sử dụng công thức phù hợp cho khe đơn hoặc khe kép để tính bước sóng \(\lambda\).
- Xác nhận kết quả: So sánh kết quả thu được với giá trị chuẩn của bước sóng để xác nhận độ chính xác của thí nghiệm.
Bài tập này giúp củng cố kiến thức về cách tính bước sóng ánh sáng thông qua các hiện tượng nhiễu xạ, từ đó hiểu rõ hơn về tính chất sóng của ánh sáng và ứng dụng của chúng trong các lĩnh vực khoa học và kỹ thuật.
Bài Tập 8: Phân Tích Hiện Tượng Nhiễu Xạ Qua Mạng Tinh Thể
Hiện tượng nhiễu xạ qua mạng tinh thể là một ứng dụng quan trọng trong vật lý học và hóa học, đặc biệt là trong việc xác định cấu trúc của các chất rắn. Khi chùm tia X hoặc ánh sáng đi qua một mạng tinh thể, nó sẽ bị nhiễu xạ, tạo ra các vân nhiễu xạ trên màn quan sát. Dựa vào các vân này, ta có thể phân tích và xác định cấu trúc của mạng tinh thể.
1. Nguyên lý nhiễu xạ qua mạng tinh thể
Mạng tinh thể có cấu trúc lặp lại trong không gian ba chiều, với các nguyên tử, ion hoặc phân tử sắp xếp theo một trật tự nhất định. Khi ánh sáng hoặc tia X chiếu vào mạng tinh thể, các sóng phản xạ từ các mặt phẳng song song trong mạng sẽ can thiệp lẫn nhau. Để xảy ra hiện tượng nhiễu xạ, cần thỏa mãn điều kiện Bragg:
Trong đó:
- \(n\) là bậc của vân nhiễu xạ (n = 1, 2, 3,...).
- \(\lambda\) là bước sóng của ánh sáng hoặc tia X.
- \(d\) là khoảng cách giữa các mặt phẳng trong mạng tinh thể.
- \(\theta\) là góc nhiễu xạ, tức là góc giữa chùm tia tới và mặt phẳng mạng tinh thể.
2. Phân tích dữ liệu nhiễu xạ để xác định cấu trúc mạng tinh thể
Khi thí nghiệm nhiễu xạ tia X được thực hiện, các vân sáng và tối sẽ xuất hiện trên phim hoặc màn quan sát. Các vị trí và cường độ của các vân này cho biết thông tin về khoảng cách giữa các mặt phẳng trong mạng tinh thể và sự sắp xếp của các nguyên tử bên trong tinh thể.
Quá trình phân tích dữ liệu nhiễu xạ bao gồm các bước sau:
- Chuẩn bị mẫu: Đặt mẫu tinh thể cần phân tích vào vị trí cố định để tia X chiếu qua.
- Chiếu tia X: Sử dụng nguồn tia X để chiếu vào mẫu tinh thể. Điều chỉnh góc chiếu và ghi lại các vân nhiễu xạ xuất hiện.
- Ghi lại dữ liệu nhiễu xạ: Sử dụng phim nhiễu xạ hoặc detector để ghi lại các vân sáng và tối.
- Phân tích vị trí và cường độ vân: Đo góc nhiễu xạ \(\theta\) và khoảng cách giữa các vân để xác định giá trị của \(d\). Sử dụng công thức Bragg để tính các tham số cấu trúc.
- Xây dựng mô hình cấu trúc tinh thể: Dựa trên dữ liệu phân tích, xây dựng mô hình cấu trúc của tinh thể, xác định vị trí và sắp xếp của các nguyên tử trong mạng.
3. Các bước thực hiện thí nghiệm và tính toán
- Xác định góc nhiễu xạ \(\theta\): Sử dụng thiết bị đo góc để xác định góc giữa chùm tia tới và các mặt phẳng mạng tinh thể tạo ra các vân nhiễu xạ rõ ràng.
- Tính khoảng cách \(d\) giữa các mặt phẳng trong mạng tinh thể: Dựa vào góc \(\theta\) đã đo được và sử dụng công thức Bragg để tính giá trị \(d\).
- Xác định bậc của vân nhiễu xạ \(n\): Phân tích dữ liệu để xác định bậc của các vân nhiễu xạ (thứ tự xuất hiện của chúng).
- Tính toán bước sóng \(\lambda\): Sử dụng các giá trị đã đo và tính toán để xác định bước sóng của tia X hoặc ánh sáng sử dụng trong thí nghiệm.
- Phân tích cấu trúc tinh thể: Sử dụng các kết quả tính toán để đưa ra kết luận về cấu trúc của mạng tinh thể.
Việc phân tích hiện tượng nhiễu xạ qua mạng tinh thể là một công cụ mạnh mẽ trong khoa học vật liệu và hóa học, giúp chúng ta hiểu rõ hơn về cấu trúc vi mô của các chất rắn và tính chất vật lý của chúng.
Bài Tập 9: Xác Định Điều Kiện Giao Thoa Tăng Cường Và Triệt Tiêu
Hiện tượng giao thoa ánh sáng xảy ra khi hai chùm sóng ánh sáng gặp nhau và tạo ra các vân sáng (tăng cường) và tối (triệt tiêu) do sự chồng chất của các sóng. Điều kiện để xảy ra giao thoa tăng cường hoặc triệt tiêu phụ thuộc vào sự khác biệt về đường đi của hai chùm sóng. Bài tập này sẽ giúp chúng ta xác định điều kiện để đạt được giao thoa tăng cường và triệt tiêu.
1. Điều kiện giao thoa tăng cường
Để hai sóng ánh sáng giao thoa và tạo ra vân sáng (tăng cường), chúng cần phải có sự khác biệt đường đi sao cho các đỉnh sóng chồng lên nhau. Điều kiện giao thoa tăng cường được xác định bởi:
Trong đó:
- \(\Delta d\) là sự chênh lệch đường đi giữa hai sóng ánh sáng.
- \(m\) là số nguyên, gọi là bậc giao thoa.
- \(\lambda\) là bước sóng của ánh sáng.
Với điều kiện này, khi hai sóng ánh sáng có sự chênh lệch đường đi bằng bội số nguyên của bước sóng, chúng sẽ chồng chất với nhau và tạo ra vân sáng trên màn quan sát.
2. Điều kiện giao thoa triệt tiêu
Để hai sóng ánh sáng giao thoa và tạo ra vân tối (triệt tiêu), sự chênh lệch đường đi của chúng phải sao cho đỉnh sóng này chồng lên đáy sóng kia. Điều kiện giao thoa triệt tiêu được xác định bởi:
Trong đó:
- \(\Delta d\) là sự chênh lệch đường đi giữa hai sóng ánh sáng.
- \(m\) là số nguyên, gọi là bậc giao thoa.
- \(\lambda\) là bước sóng của ánh sáng.
Với điều kiện này, khi hai sóng ánh sáng có sự chênh lệch đường đi bằng một nửa bước sóng cộng với bội số nguyên của bước sóng, chúng sẽ triệt tiêu lẫn nhau, tạo ra vân tối trên màn quan sát.
3. Bài tập ví dụ
Giả sử có hai chùm tia sáng đơn sắc có bước sóng \(\lambda = 600 \, \text{nm}\) chiếu qua hai khe hẹp. Khoảng cách giữa hai khe là \(d = 0.1 \, \text{mm}\) và khoảng cách từ khe đến màn quan sát là \(L = 1 \, \text{m}\).
- Xác định vị trí vân sáng bậc 1 (m = 1):
Vị trí vân sáng được xác định bởi công thức:
Thay giá trị vào, ta có:
- Xác định vị trí vân tối thứ nhất (m = 0):
Vị trí vân tối được xác định bởi công thức:
Với \(m = 0\), ta có:
Như vậy, vân sáng bậc 1 xuất hiện tại vị trí cách tâm 6 mm và vân tối thứ nhất xuất hiện tại vị trí cách tâm 3 mm.
4. Kết luận
Việc xác định điều kiện giao thoa tăng cường và triệt tiêu không chỉ giúp hiểu rõ hơn về bản chất của ánh sáng và sóng, mà còn có ứng dụng quan trọng trong nhiều lĩnh vực như quang học, truyền thông, và khoa học vật liệu.

Bài Tập 10: Tính Cường Độ Sáng Tại Một Điểm Bất Kỳ Trên Màn Quan Sát
Trong hiện tượng nhiễu xạ ánh sáng qua một khe hẹp, cường độ sáng tại một điểm bất kỳ trên màn quan sát phụ thuộc vào vị trí của điểm đó so với tâm của vân sáng trung tâm. Để tính toán cường độ sáng tại một điểm, chúng ta cần sử dụng phương trình nhiễu xạ và công thức cường độ sáng.
1. Công thức tính cường độ sáng
Cường độ sáng \(I\) tại một điểm trên màn quan sát có thể được tính bằng công thức:
Trong đó:
- \(I_0\) là cường độ sáng tại vân sáng trung tâm (cường độ cực đại).
- \(\beta = \frac{\pi a \sin(\theta)}{\lambda}\), với:
- \(a\) là bề rộng của khe hẹp.
- \(\theta\) là góc lệch từ tâm vân sáng trung tâm đến điểm đang xét.
- \(\lambda\) là bước sóng của ánh sáng.
2. Xác định các giá trị cần thiết
Để tính cường độ sáng tại một điểm bất kỳ trên màn quan sát, ta cần biết các giá trị sau:
- Bước sóng ánh sáng \(\lambda\).
- Chiều rộng của khe hẹp \(a\).
- Vị trí của điểm đang xét (góc \(\theta\) hoặc khoảng cách \(y\) từ tâm đến điểm đó).
- Cường độ sáng cực đại \(I_0\).
3. Quy trình tính toán
- Xác định giá trị \(\theta\) hoặc khoảng cách \(y\):
- Tính giá trị \(\beta\):
- Tính cường độ sáng \(I\) tại điểm đang xét:
Nếu biết khoảng cách \(y\) từ tâm vân sáng trung tâm đến điểm đang xét và khoảng cách \(L\) từ khe đến màn quan sát, ta có thể tính \(\theta\) bằng công thức:
\[ \theta \approx \tan(\theta) = \frac{y}{L} \]Với giá trị của \(\theta\) đã tìm được, ta tính \(\beta\) như sau:
\[ \beta = \frac{\pi a \sin(\theta)}{\lambda} \]Nếu \(\theta\) nhỏ, ta có thể sử dụng xấp xỉ \(\sin(\theta) \approx \theta\), do đó:
\[ \beta \approx \frac{\pi a \theta}{\lambda} \]Cuối cùng, sử dụng giá trị \(\beta\) để tính cường độ sáng \(I\) tại điểm đó:
\[ I = I_0 \left( \frac{\sin(\beta)}{\beta} \right)^2 \]4. Ví dụ tính toán
Giả sử chúng ta có một nguồn sáng đơn sắc có bước sóng \(\lambda = 500 \, \text{nm}\) chiếu qua khe hẹp có chiều rộng \(a = 0.2 \, \text{mm}\). Khoảng cách từ khe đến màn là \(L = 1 \, \text{m}\), và chúng ta muốn tính cường độ sáng tại điểm cách tâm vân sáng trung tâm \(y = 2 \, \text{mm}\).
- Tính \(\theta\): \[ \theta \approx \frac{y}{L} = \frac{2 \times 10^{-3}}{1} = 2 \times 10^{-3} \, \text{rad} \]
- Tính \(\beta\): \[ \beta = \frac{\pi \times 0.2 \times 10^{-3} \times 2 \times 10^{-3}}{500 \times 10^{-9}} = 2.513 \]
- Tính \(I\): \[ I = I_0 \left( \frac{\sin(2.513)}{2.513} \right)^2 \]
Sử dụng máy tính để tìm giá trị của biểu thức trên và tính ra cường độ sáng tại điểm đó.
5. Kết luận
Bằng cách áp dụng các công thức và quy trình trên, chúng ta có thể tính toán được cường độ sáng tại bất kỳ điểm nào trên màn quan sát trong hiện tượng nhiễu xạ ánh sáng. Điều này giúp chúng ta hiểu rõ hơn về bản chất của ánh sáng và ứng dụng trong các thí nghiệm quang học thực tế.