Chủ đề phân cực: Phân cực là hiện tượng quan trọng trong nhiều lĩnh vực như vật lý, hóa học và công nghệ. Bài viết này sẽ đưa bạn khám phá chi tiết về phân cực, từ lý thuyết đến ứng dụng thực tiễn, giúp bạn hiểu rõ hơn về vai trò của nó trong đời sống hàng ngày cũng như các ngành công nghiệp hiện đại.
Mục lục
- Hiện tượng phân cực và ứng dụng trong đời sống
- 1. Tổng quan về phân cực
- 2. Phân cực điện môi
- 3. Phân cực trong hóa học
- 4. Phân cực trong thí nghiệm điện trở cách điện
- 5. Các dạng bài tập về phân cực trong vật lý
- Bài tập 1: Phân cực của điện môi trong điện trường
- Bài tập 2: Phân cực và dung môi phân cực trong hóa học
- Bài tập 3: Phân cực và hệ số phân cực trong đo điện trở cách điện
- Bài tập 4: Sự khác biệt giữa dung môi phân cực và không phân cực
- Bài tập 5: Ứng dụng phân cực trong tụ điện
- Bài tập 6: Tính toán hệ số phân cực trong các vật liệu khác nhau
- Bài tập 7: Đo điện trở cách điện và dòng điện phân cực
- Bài tập 8: Ảnh hưởng của nhiệt độ lên phân cực điện môi
- Bài tập 9: Phân tích dòng điện hấp thụ trong cách điện
- Bài tập 10: Ứng dụng của hệ số phân cực trong kiểm tra cách điện
Hiện tượng phân cực và ứng dụng trong đời sống
Phân cực là hiện tượng quan trọng trong vật lý, đặc biệt là trong sóng điện từ. Khi sóng điện từ truyền qua một môi trường, phân cực mô tả hướng dao động của trường điện và từ trường liên quan. Hiện tượng này có ba dạng phổ biến: phân cực phẳng, phân cực tròn và phân cực elip.
Các dạng phân cực
- Phân cực phẳng: Xảy ra khi véctơ điện trường dao động theo một hướng cố định.
- Phân cực tròn: Khi véctơ điện trường xoay tròn theo thời gian tạo thành hình tròn trên mặt phẳng vuông góc với hướng truyền sóng.
- Phân cực elip: Đây là sự kết hợp giữa phân cực phẳng và tròn, tạo ra hình elip trong quá trình dao động.
Phương trình mô tả phân cực
Các trạng thái phân cực có thể được biểu diễn bằng phương trình toán học. Ví dụ, một sóng điện từ phẳng điều hòa có thể được mô tả bằng:
Trong đó:
- \(\mathbf{E}_0\) là biên độ của sóng.
- k là số sóng, mô tả sự lan truyền của sóng theo không gian.
- \(\omega\) là tần số góc, mô tả tốc độ dao động của sóng theo thời gian.
- \(\phi\) là pha ban đầu, xác định trạng thái ban đầu của dao động.
Ứng dụng của hiện tượng phân cực
Hiện tượng phân cực có nhiều ứng dụng trong đời sống, đặc biệt trong công nghệ và khoa học:
- Màn hình LCD: Ánh sáng được phân cực để điều chỉnh cường độ sáng, hiển thị hình ảnh rõ nét hơn.
- Kính phân cực: Được sử dụng trong các hoạt động ngoài trời như thể thao và nhiếp ảnh, giúp giảm lóa sáng và tăng độ rõ nét.
- Viễn thông: Sử dụng trong các hệ thống viễn thông để truyền tải tín hiệu hiệu quả hơn, giảm thiểu nhiễu sóng.
Ví dụ về phân cực trong thực tế
Khi sử dụng kính phân cực, bạn có thể nhận thấy sự giảm thiểu các tia sáng phản xạ từ mặt nước hoặc bề mặt kim loại, làm tăng độ rõ ràng của hình ảnh. Điều này được giải thích bởi việc các tia sáng này đã bị phân cực khi phản xạ từ các bề mặt, và kính phân cực ngăn cản chúng truyền tới mắt.
Ứng dụng này giúp cải thiện an toàn trong lái xe và các hoạt động thể thao ngoài trời, nơi lóa sáng có thể gây nguy hiểm.
Tác động của phân cực đến khoa học và công nghệ
Phân cực không chỉ mang tính lý thuyết mà còn là nền tảng cho nhiều công nghệ hiện đại như truyền dẫn tín hiệu không dây, y tế hình ảnh và nhiều lĩnh vực khác.
Tóm lại, phân cực là một hiện tượng tự nhiên quan trọng có ảnh hưởng lớn đến nhiều khía cạnh của khoa học và đời sống, từ công nghệ thông tin cho đến các thiết bị tiêu dùng hàng ngày.

.png)
1. Tổng quan về phân cực
Phân cực là hiện tượng vật lý quan trọng xảy ra khi sóng ánh sáng hoặc sóng điện từ bị phân chia thành hai phần với các đặc tính khác nhau. Hiện tượng này thường liên quan đến việc định hướng dao động của sóng trong không gian. Có ba loại phân cực phổ biến: phân cực phẳng, phân cực tròn và phân cực elip. Đặc biệt, phân cực được ứng dụng nhiều trong công nghệ như màn hình LCD và nhiếp ảnh.
Ví dụ về phân cực trong sóng phẳng:
- Khi \( \phi = 0^\circ \), ta có phân cực phẳng.
- Khi \( \phi = 90^\circ \), ta có phân cực tròn.
- Khi \( 0^\circ < \phi < 90^\circ \), ta có phân cực elip.
Các ứng dụng của phân cực rất đa dạng, từ khoa học kỹ thuật đến đời sống hàng ngày.
2. Phân cực điện môi
Phân cực điện môi là hiện tượng xảy ra trong các chất điện môi khi chúng được đặt trong một trường điện. Điện môi là các chất không dẫn điện nhưng có khả năng bị phân cực, nghĩa là các phân tử hoặc nguyên tử bên trong chất điện môi có thể sắp xếp lại theo chiều của trường điện, tạo ra các lưỡng cực điện.
Khi một chất điện môi nằm trong trường điện ngoài, các lưỡng cực điện sẽ bị ảnh hưởng bởi lực điện và tạo thành một phân cực trong vật liệu. Các loại phân cực điện môi bao gồm:
- Phân cực điện tử: Xảy ra khi các đám mây điện tử của nguyên tử bị dịch chuyển do tác động của trường điện.
- Phân cực ion: Xảy ra khi các ion dương và âm trong một phân tử bị kéo ra xa nhau dưới tác động của trường điện.
- Phân cực định hướng: Xảy ra khi các phân tử có mômen lưỡng cực sẵn có quay theo hướng của trường điện ngoài.
Mức độ phân cực điện môi phụ thuộc vào cường độ của trường điện và tính chất của chất điện môi. Công thức phân cực điện môi được thể hiện qua:
Trong đó:
- \(P\) là độ phân cực (C/m²)
- \(\epsilon_0\) là hằng số điện môi chân không (8.854 x 10⁻¹² F/m)
- \(\epsilon_r\) là hằng số điện môi tương đối của vật liệu
- \(E\) là cường độ điện trường (V/m)
Phân cực điện môi có vai trò quan trọng trong các ứng dụng thực tế như sản xuất tụ điện, vật liệu cách điện và các hệ thống viễn thông.

3. Phân cực trong hóa học
Phân cực trong hóa học là hiện tượng xảy ra khi các nguyên tử trong một liên kết hóa học không chia sẻ electron một cách đồng đều, dẫn đến sự hình thành các lưỡng cực điện. Điều này xảy ra do sự khác biệt về độ âm điện giữa các nguyên tử trong liên kết.
Trong phân tử, khi có sự phân bố không đều của mật độ electron, phân tử sẽ có hai đầu: một đầu tích điện dương và một đầu tích điện âm, tạo ra lưỡng cực. Liên kết được gọi là phân cực khi:
- Sự khác biệt độ âm điện giữa hai nguyên tử là đáng kể (thường lớn hơn 0.5).
- Các cặp electron không được chia sẻ đồng đều.
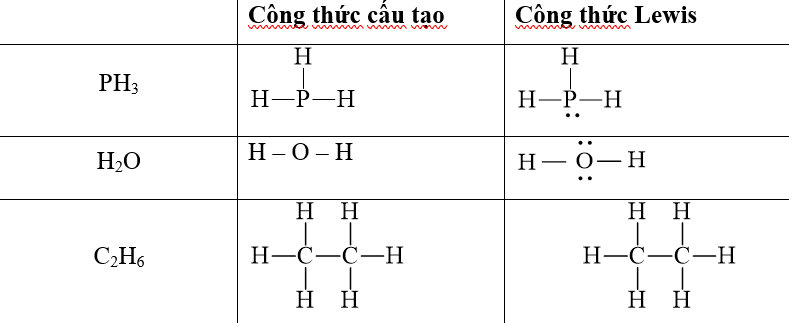
Một ví dụ tiêu biểu về phân cực hóa học là liên kết trong phân tử nước (H2O), nơi mà oxy có độ âm điện cao hơn so với hydro. Điều này tạo ra một lưỡng cực với đầu oxy tích điện âm và đầu hydro tích điện dương.
Công thức mô tả momen lưỡng cực \( \mu \) là:
Trong đó:
- \( \mu \) là momen lưỡng cực (Debye)
- \( q \) là độ lớn của điện tích (Coulomb)
- \( r \) là khoảng cách giữa hai điện tích (m)
Phân cực có ảnh hưởng lớn đến tính chất vật lý và hóa học của các chất, ví dụ như độ hòa tan trong dung môi, tính dẫn điện và nhiệt độ sôi của các chất. Trong các phản ứng hóa học, sự phân cực đóng vai trò quan trọng trong việc xác định cơ chế phản ứng và tính chất của sản phẩm.

XEM THÊM:
4. Phân cực trong thí nghiệm điện trở cách điện
Phân cực trong thí nghiệm điện trở cách điện là một hiện tượng quan trọng cần phải hiểu rõ khi thực hiện các phép đo đánh giá chất lượng cách điện của vật liệu. Quá trình phân cực xảy ra khi một điện trường được đặt lên một vật liệu cách điện, dẫn đến sự dịch chuyển của các phân tử và ion trong vật liệu, tạo ra các lưỡng cực điện.
Thí nghiệm điện trở cách điện thường sử dụng một nguồn điện áp cao, đặt lên vật liệu cách điện, và đo dòng điện rò chảy qua vật liệu này. Khi xảy ra phân cực, các phân tử và ion trong cách điện sẽ sắp xếp lại, làm tăng hoặc giảm giá trị điện trở đo được theo thời gian.
Quá trình phân cực có thể ảnh hưởng đến độ chính xác của các kết quả đo điện trở cách điện và được biểu diễn thông qua các đại lượng như:
- Điện trở ban đầu \( R_0 \): Điện trở đo được ngay khi áp đặt điện trường.
- Điện trở phân cực \( R_p \): Điện trở tăng lên sau một thời gian khi các phân tử đã sắp xếp lại.
Biểu thức tổng quát cho điện trở cách điện \( R \) khi xảy ra phân cực có thể được biểu diễn như sau:
Trong đó:
- \( R_0 \) là điện trở ban đầu (ohm)
- \( R_p \) là điện trở do phân cực (ohm)
Thời gian thí nghiệm cũng rất quan trọng, vì giá trị điện trở cách điện sẽ thay đổi theo thời gian do sự phân cực của vật liệu. Để có được kết quả chính xác, người ta thường đo điện trở cách điện trong nhiều khoảng thời gian khác nhau và tính trung bình kết quả.
Việc hiểu rõ phân cực trong thí nghiệm điện trở cách điện giúp xác định chính xác tình trạng của cách điện và đưa ra các biện pháp bảo dưỡng, thay thế phù hợp.

5. Các dạng bài tập về phân cực trong vật lý
Phân cực trong vật lý là một chủ đề quan trọng, đặc biệt trong các hiện tượng liên quan đến sóng điện từ và ánh sáng. Dưới đây là các dạng bài tập phổ biến về phân cực, kèm theo lời giải chi tiết, giúp học sinh nắm vững kiến thức:
- Bài tập 1: Tính cường độ ánh sáng sau khi đi qua hai bản phân cực.
- Bài tập 2: Xác định góc phân cực của một chất khi biết chiết suất.
- Bài tập 3: Tính phần trăm ánh sáng bị phân cực khi phản xạ trên mặt nước.
- Bài tập 4: Giải bài toán về ánh sáng phân cực và lưỡng chiết.
- Bài tập 5: Xác định tỉ lệ ánh sáng phân cực qua các lớp vật liệu.
- Bài tập 6: Tính cường độ ánh sáng phân cực toàn phần.
- Bài tập 7: Giải bài toán về phân cực kép.
- Bài tập 8: Xác định góc Brewster cho các vật liệu có chiết suất khác nhau.
- Bài tập 9: Bài toán về phân cực và cường độ ánh sáng qua kính phân cực.
- Bài tập 10: Phân tích hiện tượng phân cực ánh sáng qua lớp mỏng.
Giả sử ánh sáng không phân cực có cường độ ban đầu \( I_0 \). Ánh sáng đi qua bản phân cực đầu tiên có cường độ \( I_1 = \frac{I_0}{2} \). Sau khi đi qua bản phân cực thứ hai với góc lệch \( \theta \) so với bản đầu tiên, cường độ ánh sáng sẽ là:
\[ I_2 = I_1 \cos^2(\theta) \]Với lời giải, học sinh cần tính toán giá trị cụ thể dựa trên dữ liệu bài toán.
Góc phân cực \( \theta_p \) của một chất được xác định thông qua công thức Brewster:
\[ \tan(\theta_p) = n \]Trong đó, \( n \) là chiết suất của chất. Học sinh tính toán dựa trên giá trị chiết suất được cung cấp.
Ánh sáng phản xạ từ bề mặt nước sẽ bị phân cực theo một mức độ nhất định. Học sinh cần sử dụng công thức tính hệ số phản xạ và phân cực.
Bài tập này yêu cầu học sinh xác định sự phân cực của ánh sáng khi đi qua các môi trường có hiện tượng lưỡng chiết.
Sử dụng công thức Fresnel để tính tỉ lệ ánh sáng bị phân cực khi đi qua nhiều lớp vật liệu khác nhau.
Sử dụng công thức liên quan đến độ lệch và góc phân cực để tính cường độ ánh sáng.
Bài toán này yêu cầu học sinh giải quyết hiện tượng ánh sáng phân cực qua hai vật liệu phân cực khác nhau.
Áp dụng công thức Brewster để tính góc cho mỗi vật liệu khác nhau.
Tính toán cường độ ánh sáng sau khi đi qua nhiều kính phân cực đặt ở các góc khác nhau.
Bài toán yêu cầu xác định sự phân cực khi ánh sáng đi qua lớp mỏng có độ dày khác nhau.
Những dạng bài tập này giúp học sinh nắm vững kiến thức về phân cực và áp dụng vào các hiện tượng vật lý liên quan.
Bài tập 1: Phân cực của điện môi trong điện trường
Khi một điện môi được đặt trong điện trường ngoài, các phân tử của nó sẽ trải qua hiện tượng phân cực. Bài tập này yêu cầu chúng ta tính toán mật độ phân cực \( P \) của điện môi khi đặt trong điện trường ngoài \( E \).
Bài toán: Giả sử một điện môi có hằng số điện môi \( \varepsilon_r \) và được đặt trong điện trường ngoài \( E \). Xác định mật độ phân cực \( P \) của điện môi.
- Bước 1: Tính cường độ phân cực \( P \).
- \( \varepsilon_0 \) là hằng số điện môi của chân không.
- \( \chi_e \) là độ cảm điện của điện môi.
- \( E \) là cường độ điện trường ngoài.
- Bước 2: Xác định độ cảm điện \( \chi_e \).
- Bước 3: Thay số vào công thức.
- Bước 4: Tính kết quả cuối cùng.
Công thức liên hệ giữa mật độ phân cực \( P \) và điện trường ngoài \( E \) là:
\[ P = \varepsilon_0 \chi_e E \]Trong đó:
Độ cảm điện \( \chi_e \) có thể được tính từ hằng số điện môi \( \varepsilon_r \) bằng công thức:
\[ \chi_e = \varepsilon_r - 1 \]Giả sử \( \varepsilon_r = 5 \) và \( E = 1000 \, \text{V/m} \), ta có:
\[ \chi_e = 5 - 1 = 4 \]Thay vào công thức tính mật độ phân cực:
\[ P = \varepsilon_0 \cdot 4 \cdot 1000 \, \text{V/m} \]Với \( \varepsilon_0 = 8.854 \times 10^{-12} \, \text{F/m} \), ta tính được mật độ phân cực \( P \).
Áp dụng các giá trị đã biết, ta tính được giá trị của \( P \) là:
\[ P = 3.5416 \times 10^{-8} \, \text{C/m}^2 \]Như vậy, mật độ phân cực của điện môi khi đặt trong điện trường ngoài là \( 3.5416 \times 10^{-8} \, \text{C/m}^2 \).

Bài tập 2: Phân cực và dung môi phân cực trong hóa học
Dung môi phân cực đóng vai trò quan trọng trong hóa học, đặc biệt trong các phản ứng cần thiết sự hòa tan của các hợp chất ion hoặc hợp chất có liên kết phân cực. Dưới đây là một số bài tập liên quan đến phân cực và dung môi phân cực trong hóa học.
Bài tập:
-
Giải thích tại sao nước là một dung môi phân cực mạnh. Sử dụng cấu trúc phân tử và độ âm điện để hỗ trợ câu trả lời.
-
Xác định liệu các dung môi sau đây có phân cực hay không phân cực: etanol, hexan, benzen, methanol. Giải thích lý do tại sao.
Gợi ý: Xem xét sự khác biệt trong cấu trúc phân tử và sự phân bố điện tích trong mỗi dung môi.
-
Tính toán năng lượng tương tác giữa hai phân tử nước bằng cách sử dụng mô hình lưỡng cực-lưỡng cực, với khoảng cách giữa hai phân tử là 3 Å. Sử dụng công thức sau:
\[
E = -\frac{{\mu_1 \cdot \mu_2}}{{4\pi\epsilon_0 r^3}} \left(1 - 3\cos^2\theta\right)
\]Trong đó:
- \( \mu_1 \) và \( \mu_2 \) là mômen lưỡng cực của hai phân tử nước.
- \( r \) là khoảng cách giữa hai phân tử.
- \( \theta \) là góc giữa các mômen lưỡng cực.
Phân biệt giữa dung môi phân cực và dung môi không phân cực trong việc hòa tan các hợp chất ion. Sử dụng ví dụ cụ thể về NaCl và hexan.
-
Một dung môi có hằng số điện môi cao có ảnh hưởng như thế nào đến khả năng hòa tan của các hợp chất ion? So sánh giữa nước và dầu.
-
Giải thích tại sao dung môi phân cực có khả năng hòa tan tốt các hợp chất có nhóm chức phân cực như -OH, -NH2.
-
Tìm hiểu vai trò của dung môi phân cực trong phản ứng SN1 và SN2. Làm thế nào dung môi phân cực có thể ảnh hưởng đến tốc độ phản ứng trong từng trường hợp?
Kết luận:
Bài tập này nhằm mục đích giúp học sinh hiểu rõ hơn về bản chất của dung môi phân cực, các tính chất và ứng dụng của chúng trong hóa học. Sự phân cực không chỉ ảnh hưởng đến tính chất hòa tan mà còn đóng vai trò quan trọng trong cơ chế và tốc độ phản ứng hóa học.

Bài tập 3: Phân cực và hệ số phân cực trong đo điện trở cách điện
Trong quá trình đo điện trở cách điện, một khái niệm quan trọng cần hiểu rõ là hiện tượng phân cực và hệ số phân cực (PI). Hệ số phân cực là một chỉ số thể hiện mức độ suy giảm của vật liệu cách điện trong suốt quá trình đo.
Khi đo điện trở cách điện, bạn thường tiến hành trong một khoảng thời gian nhất định, ví dụ từ 1 phút đến 10 phút. Hệ số phân cực (PI) được tính bằng cách lấy tỷ lệ giữa giá trị đo điện trở cách điện ở phút thứ 10 và giá trị đo ở phút thứ 1:
Một số bước cơ bản để thực hiện đo điện trở cách điện và tính hệ số phân cực bao gồm:
- Chuẩn bị thiết bị đo: Đảm bảo thiết bị đo điện trở cách điện (megohmmeters) được cấu hình đúng và phù hợp với tiêu chuẩn yêu cầu.
- Kết nối thiết bị: Kết nối thiết bị đo với đối tượng cần kiểm tra, như động cơ điện, máy phát điện, hoặc hệ thống cáp điện.
- Tiến hành đo: Bắt đầu quá trình đo và ghi lại giá trị điện trở cách điện ở phút đầu tiên và phút thứ 10.
- Tính toán hệ số phân cực: Sử dụng công thức trên để tính toán PI. Một PI > 2.0 được coi là tốt, trong khi PI < 1.0 có thể cho thấy cách điện bị suy giảm nghiêm trọng.
Việc đo lường chính xác và đánh giá đúng hệ số phân cực giúp bạn xác định được tình trạng của vật liệu cách điện, từ đó đưa ra các biện pháp bảo trì, sửa chữa kịp thời.
Dưới đây là một bảng tóm tắt về hệ số phân cực theo các lớp cách điện:
| Lớp cách điện | Hệ số phân cực (PI) tối thiểu |
|---|---|
| Lớp A | 1.5 |
| Lớp B | 2.0 |
| Lớp C | 2.0 |
Việc hiểu rõ và áp dụng đúng các phương pháp đo điện trở cách điện không chỉ giúp đảm bảo an toàn cho hệ thống điện mà còn kéo dài tuổi thọ của thiết bị.
Bài tập 4: Sự khác biệt giữa dung môi phân cực và không phân cực
Trong hóa học, dung môi đóng vai trò quan trọng trong việc hòa tan các chất khác nhau, tùy thuộc vào tính chất phân cực của chúng. Dung môi được chia thành hai loại chính: dung môi phân cực và dung môi không phân cực. Sự khác biệt giữa hai loại dung môi này có thể ảnh hưởng lớn đến quá trình hòa tan và các phản ứng hóa học liên quan.
1. Dung môi phân cực:
- Dung môi phân cực có momen lưỡng cực, tức là chúng có sự phân bố điện tích không đồng đều trong phân tử.
- Các dung môi này thường có khả năng hòa tan tốt các hợp chất phân cực, nhờ vào sự tương tác giữa các điện tích trái dấu.
- Một số ví dụ về dung môi phân cực phổ biến bao gồm: nước \((H_2O)\), methanol \((CH_3OH)\), ethanol \((CH_3CH_2OH)\), và acetonitrile \((CH_3CN)\).
- Dung môi phân cực được sử dụng rộng rãi trong các phản ứng hóa học, đặc biệt là trong các cơ chế phản ứng như SN1 và SN2.
2. Dung môi không phân cực:
- Dung môi không phân cực không có momen lưỡng cực, nghĩa là các phân tử của chúng không có sự phân bố điện tích.
- Chúng không thể hòa tan các hợp chất phân cực, nhưng lại rất hiệu quả trong việc hòa tan các chất không phân cực.
- Một số ví dụ về dung môi không phân cực bao gồm: hexan \((C_6H_{14})\), benzen \((C_6H_6)\), và toluen \((C_7H_8)\).
- Dung môi không phân cực thường được sử dụng trong các ngành công nghiệp như dầu mỏ, hóa chất, và sơn.
3. Sự khác biệt chính:
- Sự khác biệt chính giữa dung môi phân cực và không phân cực nằm ở khả năng tương tác với các chất hòa tan dựa trên tính chất điện tích của chúng.
- Dung môi phân cực có thể hòa tan các hợp chất phân cực nhờ vào tương tác giữa các điện tích, trong khi dung môi không phân cực chỉ hòa tan được các hợp chất không phân cực.
- Điều này dẫn đến việc lựa chọn dung môi thích hợp là yếu tố quan trọng trong việc tối ưu hóa các phản ứng hóa học và quy trình công nghiệp.

Bài tập 5: Ứng dụng phân cực trong tụ điện
Tụ điện là một trong những thành phần quan trọng trong các mạch điện tử, đặc biệt là tụ điện phân cực, loại tụ có đặc điểm hai đầu cực âm và dương rõ rệt. Tụ điện phân cực được ứng dụng rộng rãi trong các mạch có tần số thấp và mạch lọc nguồn. Dưới đây là một số ứng dụng cụ thể và cách tính toán liên quan đến phân cực trong tụ điện:
- Ứng dụng trong mạch lọc nguồn: Tụ điện phân cực được sử dụng để lọc nhiễu trong mạch điện, đặc biệt là trong các bộ nguồn DC. Khi kết nối vào mạch, tụ điện giúp giảm thiểu tiếng ồn và sóng điện áp không mong muốn, từ đó ổn định dòng điện cung cấp cho các thiết bị điện tử.
- Ứng dụng trong mạch khuếch đại âm thanh: Trong các bộ khuếch đại âm thanh, tụ điện phân cực đóng vai trò quan trọng trong việc loại bỏ tiếng ồn từ nguồn điện, đặc biệt là các tiếng ồn ở tần số 50Hz hoặc 60Hz.
- Tính toán điện dung: Khi sử dụng tụ điện phân cực, việc tính toán điện dung yêu cầu phải xem xét cả điện dung tổng thể của mạch và các yếu tố khác như tần số và điện áp hoạt động. Công thức cơ bản để tính điện dung trong mạch có thể được biểu diễn như sau:
\[ C = \frac{Q}{V} \]
Trong đó:
- \( C \) là điện dung (đơn vị là Farad).
- \( Q \) là điện tích lưu trữ trên bản cực của tụ điện (đơn vị là Coulomb).
- \( V \) là điện áp giữa hai bản cực của tụ điện (đơn vị là Volt).
Từ công thức trên, ta có thể tính toán các thông số cần thiết khi thiết kế mạch điện sử dụng tụ điện phân cực, nhằm đảm bảo hiệu suất và độ bền của tụ điện trong mạch.
Kết luận, tụ điện phân cực có vai trò quan trọng trong việc ổn định dòng điện và lọc nhiễu trong các hệ thống điện tử, đặc biệt là trong các mạch tần số thấp. Việc hiểu rõ các ứng dụng của phân cực trong tụ điện giúp tối ưu hóa thiết kế mạch và đảm bảo an toàn trong quá trình sử dụng.
Bài tập 6: Tính toán hệ số phân cực trong các vật liệu khác nhau
Trong lĩnh vực vật liệu, hệ số phân cực đóng vai trò quan trọng trong việc xác định các tính chất điện của vật liệu. Hệ số này biểu thị mức độ phân cực của các phân tử hoặc nguyên tử trong một chất khi bị tác động bởi một trường điện. Để hiểu rõ hơn về cách tính toán hệ số phân cực, chúng ta sẽ đi sâu vào từng bước như sau:
- Hiểu khái niệm mô men lưỡng cực: Mô men lưỡng cực (μ) được định nghĩa là tích của điện tích (\(q\)) và khoảng cách (\(d\)) giữa các điện tích đối nhau, được biểu diễn bằng công thức: \[ \mu = q \cdot d \] Trong đó, \(q\) là độ lớn của điện tích và \(d\) là khoảng cách giữa hai điện tích.
- Thu thập dữ liệu về vật liệu: Để tính toán hệ số phân cực, trước tiên cần xác định các thông số điện tích và khoảng cách trong các vật liệu cụ thể. Các vật liệu có hệ số phân cực cao thường có các liên kết phân cực mạnh hoặc mô men lưỡng cực lớn.
- Sử dụng công thức tính hệ số phân cực: Hệ số phân cực có thể được tính toán bằng cách áp dụng công thức mô men lưỡng cực cho từng loại vật liệu. Ví dụ: \[ \mu = \sum_{i} q_i \cdot d_i \] trong đó \(q_i\) và \(d_i\) là các giá trị tương ứng cho từng phân tử hoặc nguyên tử trong vật liệu.
- Phân tích kết quả: Sau khi tính toán, hệ số phân cực giúp chúng ta đánh giá khả năng của vật liệu trong việc tương tác với các trường điện. Vật liệu có hệ số phân cực cao thường được sử dụng trong các ứng dụng yêu cầu khả năng cách điện tốt hoặc trong các thiết bị điện tử.
Hệ số phân cực là một chỉ số quan trọng trong nghiên cứu và ứng dụng vật liệu. Bằng cách hiểu và tính toán chính xác hệ số này, chúng ta có thể dự đoán và tối ưu hóa tính chất của vật liệu trong các ứng dụng thực tế.
Bài tập 7: Đo điện trở cách điện và dòng điện phân cực
Trong bài tập này, chúng ta sẽ khám phá cách đo điện trở cách điện và dòng điện phân cực của các vật liệu điện. Để tiến hành đo lường, chúng ta sẽ cần đến các thiết bị đo điện và một số kiến thức cơ bản về phân cực.
Bước 1: Chuẩn bị các thiết bị cần thiết bao gồm:
- Máy đo điện trở cách điện (Megohmmeter)
- Đồng hồ đo dòng điện (Ammeter)
- Vật liệu mẫu cần đo
Bước 2: Kết nối các thiết bị theo sơ đồ mạch điện:
- Kết nối một đầu của máy đo điện trở cách điện vào cực dương của nguồn điện.
- Đầu còn lại của máy đo nối với một điện cực của vật liệu cần đo.
- Kết nối đồng hồ đo dòng điện nối tiếp với mạch để đo dòng điện phân cực chạy qua vật liệu.
Bước 3: Tiến hành đo điện trở cách điện:
Khi áp điện áp lên vật liệu, máy đo điện trở cách điện sẽ đo giá trị điện trở của vật liệu. Điện trở cách điện được xác định theo công thức:
\[ R = \frac{V}{I} \]
Trong đó:
- \(R\) là điện trở cách điện (Ohm)
- \(V\) là điện áp đặt vào (Volt)
- \(I\) là dòng điện phân cực (Ampere)
Bước 4: Đo dòng điện phân cực:
Sau khi xác định được điện trở cách điện, đồng hồ đo dòng điện sẽ hiển thị giá trị dòng điện phân cực. Đây là dòng điện nhỏ chạy qua vật liệu khi điện áp được áp dụng, phản ánh mức độ phân cực của vật liệu.
Bước 5: Ghi lại kết quả đo:
| Vật liệu | Điện trở cách điện (Ohm) | Dòng điện phân cực (A) |
|---|---|---|
| Vật liệu A | \(R_A\) | \(I_A\) |
| Vật liệu B | \(R_B\) | \(I_B\) |
Bước 6: Phân tích kết quả:
Sau khi ghi nhận các giá trị, bạn cần so sánh điện trở cách điện và dòng điện phân cực của các vật liệu để đánh giá độ cách điện và mức độ phân cực của chúng.

Bài tập 8: Ảnh hưởng của nhiệt độ lên phân cực điện môi
Nhiệt độ là một yếu tố quan trọng ảnh hưởng đến sự phân cực của điện môi, bởi vì khi nhiệt độ thay đổi, cấu trúc và động học của các phân tử trong vật liệu điện môi cũng thay đổi. Sự thay đổi này dẫn đến các hiện tượng như tăng hoặc giảm độ phân cực, từ đó ảnh hưởng trực tiếp đến các tính chất điện của vật liệu.
Khi nhiệt độ tăng, các phân tử trong điện môi nhận năng lượng và dao động mạnh hơn, làm giảm khả năng phân cực của các phân tử. Điều này có thể được minh họa qua công thức:
Trong đó:
- \(P\) là độ phân cực của vật liệu.
- \(\alpha\) là hệ số phân cực, thường giảm khi nhiệt độ tăng.
- \(E\) là điện trường ngoài.
Như vậy, ở nhiệt độ cao, hệ số phân cực \(\alpha\) có xu hướng giảm, làm giảm tổng độ phân cực \(P\). Kết quả là khả năng cách điện của vật liệu cũng bị giảm đi, do đó hiệu suất hoạt động của thiết bị sử dụng điện môi có thể bị ảnh hưởng. Điều này đặc biệt quan trọng khi thiết kế các thiết bị điện tử, cần phải đảm bảo rằng các vật liệu cách điện được sử dụng có thể duy trì tính chất điện môi ổn định trong dải nhiệt độ hoạt động rộng.
Bài tập này yêu cầu bạn phân tích sự thay đổi của hệ số phân cực trong các loại điện môi khác nhau khi nhiệt độ thay đổi. Hãy sử dụng các công thức và số liệu thực nghiệm để xác định hệ số phân cực ở các mức nhiệt độ khác nhau và so sánh kết quả. Đặc biệt, cần lưu ý đến các hiện tượng như điện dẫn nhiệt độ và các yếu tố môi trường khác có thể ảnh hưởng đến kết quả đo đạc.
Ví dụ về một bài toán tính toán có thể bao gồm:
- Tính toán hệ số phân cực của một mẫu điện môi tại nhiệt độ phòng (\(25^\circ C\)) và so sánh với hệ số phân cực tại nhiệt độ cao hơn (\(100^\circ C\)).
- Phân tích và giải thích sự khác biệt trong kết quả, liên hệ với các hiện tượng vật lý như sự thay đổi trong cấu trúc phân tử, mức độ phân cực, và ảnh hưởng của nhiệt độ lên các thông số này.
Qua bài tập này, bạn sẽ nắm được cách nhiệt độ ảnh hưởng đến các đặc tính của vật liệu điện môi, từ đó có thể ứng dụng vào thực tiễn trong việc lựa chọn và sử dụng vật liệu cách điện trong các thiết bị điện tử và hệ thống điện.
Bài tập 9: Phân tích dòng điện hấp thụ trong cách điện
Trong hệ thống cách điện, dòng điện hấp thụ đóng vai trò quan trọng trong việc đánh giá chất lượng của vật liệu cách điện. Khi một điện áp được đặt vào cách điện, dòng điện hấp thụ xuất hiện do sự phân cực của các điện môi. Bài tập này sẽ giúp bạn hiểu rõ hơn về quá trình phân cực và phân tích dòng điện hấp thụ trong các vật liệu cách điện.
Bước 1: Hiểu về dòng điện hấp thụ
- Dòng điện hấp thụ là dòng điện sinh ra khi điện môi trong vật liệu cách điện bị phân cực dưới tác động của điện trường.
- Quá trình này liên quan đến sự dịch chuyển của các điện tích và sự định hướng của các lưỡng cực bên trong vật liệu.
Bước 2: Phân tích các yếu tố ảnh hưởng
- Độ lớn của điện trường: Điện trường càng mạnh thì dòng điện hấp thụ càng lớn do sự phân cực mạnh hơn.
- Thời gian áp điện áp: Dòng điện hấp thụ thường giảm dần theo thời gian khi vật liệu cách điện đạt trạng thái cân bằng.
- Nhiệt độ: Nhiệt độ cao có thể làm tăng tốc độ phân cực, do đó ảnh hưởng đến dòng điện hấp thụ.
Bước 3: Đo dòng điện hấp thụ
- Sử dụng thiết bị đo điện trở cách điện (IR Tester) để đo dòng điện hấp thụ tại các thời điểm khác nhau sau khi áp điện áp.
- Số liệu thu được giúp đánh giá chất lượng của vật liệu cách điện, phát hiện sự suy giảm hoặc hỏng hóc.
Bước 4: Áp dụng kết quả vào thực tế
Kết quả đo dòng điện hấp thụ có thể được sử dụng để đánh giá và cải thiện hệ thống cách điện, đảm bảo hiệu suất hoạt động và an toàn cho các thiết bị điện.
Bài tập 10: Ứng dụng của hệ số phân cực trong kiểm tra cách điện
Hệ số phân cực là một trong những yếu tố quan trọng được sử dụng trong kiểm tra cách điện của vật liệu. Dưới đây là quy trình kiểm tra và ứng dụng của hệ số này:
- Chuẩn bị thiết bị:
- Máy đo điện trở cách điện.
- Điện cực để tạo điện trường trong mẫu vật liệu cần kiểm tra.
- Đồng hồ đo hệ số phân cực.
- Tiến hành đo điện trở cách điện:
Đặt điện cực vào vị trí cần kiểm tra trên vật liệu. Sau đó, sử dụng máy đo để xác định điện trở cách điện tại thời điểm ban đầu (t0) và sau một khoảng thời gian xác định (t1).
- Ghi lại các giá trị điện trở ở cả hai thời điểm.
- Tính toán hệ số phân cực:
Hệ số phân cực (\(PI\)) được tính toán dựa trên tỷ số giữa giá trị điện trở đo được sau một khoảng thời gian (\(R(t_1)\)) và điện trở ban đầu (\(R(t_0)\)):
\[
PI = \frac{R(t_1)}{R(t_0)}
\]Thông thường, \(t_1\) là 10 phút và \(t_0\) là 1 phút. Giá trị \(PI\) càng cao cho thấy vật liệu có khả năng cách điện tốt hơn.
- Đánh giá kết quả:
- Hệ số phân cực từ 2.0 trở lên: Cách điện tốt, vật liệu an toàn khi sử dụng.
- Hệ số phân cực từ 1.0 đến 2.0: Cách điện trung bình, cần kiểm tra thêm.
- Hệ số phân cực dưới 1.0: Cách điện kém, vật liệu không an toàn.
- Ứng dụng trong thực tế:
Hệ số phân cực được sử dụng rộng rãi trong việc kiểm tra chất lượng của cách điện trên các thiết bị điện như cáp điện, máy biến áp, và các hệ thống điện khác. Bằng cách đo lường hệ số phân cực, kỹ sư có thể đánh giá chính xác mức độ an toàn và tuổi thọ của vật liệu cách điện, từ đó đề ra các biện pháp bảo trì phù hợp.
Với quy trình và các bước kiểm tra như trên, hệ số phân cực là một công cụ hữu ích giúp đảm bảo an toàn trong việc sử dụng các thiết bị và vật liệu điện trong ngành công nghiệp.