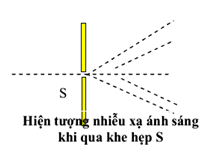
Chủ đề nhiễu xạ qua 1 khe hẹp: Nhiễu xạ qua 1 khe hẹp là một trong những hiện tượng quan trọng giúp minh chứng cho bản chất sóng của ánh sáng. Bài viết này sẽ giúp bạn hiểu rõ hơn về nguyên lý, ứng dụng và các bài tập liên quan đến hiện tượng nhiễu xạ, đồng thời khám phá những kiến thức thú vị và hữu ích về vật lý sóng.
Mục lục
- Tổng Quan Về Hiện Tượng Nhiễu Xạ Qua Một Khe Hẹp
- 1. Tổng Quan Về Hiện Tượng Nhiễu Xạ Qua 1 Khe Hẹp
- 2. Phương Trình Tính Toán Nhiễu Xạ
- 3. Ứng Dụng Hiện Tượng Nhiễu Xạ Trong Đời Sống
- 4. Thí Nghiệm Về Nhiễu Xạ Qua 1 Khe Hẹp
- 5. 10 Dạng Bài Tập Nhiễu Xạ Qua 1 Khe Hẹp Có Lời Giải Hoàn Chỉnh
- Dạng Bài Tập 1: Tính Toán Vị Trí Vân Sáng Trung Tâm
- Dạng Bài Tập 2: Xác Định Vị Trí Các Vân Sáng Phụ
- Dạng Bài Tập 3: Tính Toán Góc Nhiễu Xạ Tối Thiểu
- Dạng Bài Tập 4: Tính Độ Rộng Vân Sáng Trung Tâm
- Dạng Bài Tập 5: Ảnh Hưởng Của Bước Sóng Đến Hình Dạng Nhiễu Xạ
- Dạng Bài Tập 6: Phân Tích Thí Nghiệm Nhiễu Xạ Qua Khe Hẹp
- Dạng Bài Tập 7: So Sánh Nhiễu Xạ Qua Khe Hẹp Và Nhiễu Xạ Qua Cách Tử
- Dạng Bài Tập 8: Tính Cường Độ Sáng Tại Các Vị Trí Khác Nhau
- Dạng Bài Tập 9: Xác Định Khoảng Cách Giữa Các Vân Sáng
- Dạng Bài Tập 10: Ứng Dụng Hiện Tượng Nhiễu Xạ Trong Thực Tiễn
Tổng Quan Về Hiện Tượng Nhiễu Xạ Qua Một Khe Hẹp
Nhiễu xạ qua một khe hẹp là hiện tượng xảy ra khi sóng ánh sáng (hoặc sóng khác) đi qua một khe hẹp và lan tỏa ra theo các hướng khác nhau. Đây là một hiện tượng quan trọng trong vật lý sóng và đã được nghiên cứu kỹ lưỡng trong các thí nghiệm và lý thuyết về sóng ánh sáng.
Nguyên Lý Cơ Bản
Theo nguyên lý Huygens-Fresnel, mỗi điểm trên mặt sóng khi đi qua khe hẹp có thể coi như một nguồn phát sóng thứ cấp. Những sóng này giao thoa với nhau, dẫn đến sự hình thành các vùng sáng và tối trên màn quan sát phía sau khe hẹp.
Các Vân Sáng và Tối
Trên màn quan sát, ta có thể thấy các vân sáng và tối luân phiên nhau. Vân sáng trung tâm là sáng nhất, do các tia sáng hội tụ tại điểm đó, còn các vân sáng phụ có cường độ nhỏ hơn rất nhiều. Các vân tối xuất hiện ở những vị trí mà sóng từ các phần khác nhau của khe hẹp triệt tiêu lẫn nhau.
Phương Trình Tính Toán
- Điều kiện vân sáng: \(\sin \phi = \frac{(2k+1)\lambda}{2b}\), với \(k = 0, \pm 1, \pm 2,...\)
- Điều kiện vân tối: \(\sin \phi = \frac{k\lambda}{b}\), với \(k = \pm 1, \pm 2,...\)
Ở đây, \(\phi\) là góc nhiễu xạ, \(\lambda\) là bước sóng ánh sáng, và \(b\) là độ rộng của khe hẹp.
Ứng Dụng và Ý Nghĩa
Hiện tượng nhiễu xạ không chỉ giúp ta hiểu sâu hơn về tính chất sóng của ánh sáng mà còn có nhiều ứng dụng thực tiễn trong các lĩnh vực như quang học, nhiếp ảnh, và nghiên cứu khoa học.
Kết Luận
Nhiễu xạ qua một khe hẹp là một trong những hiện tượng quan trọng để minh chứng cho bản chất sóng của ánh sáng. Việc nắm vững các nguyên lý của hiện tượng này giúp chúng ta áp dụng vào nhiều lĩnh vực khác nhau trong khoa học và kỹ thuật.

.png)
1. Tổng Quan Về Hiện Tượng Nhiễu Xạ Qua 1 Khe Hẹp
Nhiễu xạ qua 1 khe hẹp là một hiện tượng quang học nổi bật, được giải thích bằng bản chất sóng của ánh sáng. Khi sóng ánh sáng đi qua một khe hẹp, chúng không chỉ truyền thẳng mà còn uốn cong, tạo ra các vân sáng và tối xen kẽ trên màn hứng phía sau. Hiện tượng này giúp xác định tính chất sóng của ánh sáng, giải thích cách thức mà ánh sáng phân bố sau khi gặp vật cản.
Để hiểu rõ hiện tượng này, cần xem xét mối liên hệ giữa kích thước khe hẹp và bước sóng ánh sáng. Khi ánh sáng có bước sóng tương đương với chiều rộng khe, nhiễu xạ xảy ra rõ rệt nhất. Công thức chính để mô tả hiện tượng này là:
Trong đó:
- \(a\) là chiều rộng của khe hẹp.
- \(\theta\) là góc nhiễu xạ.
- \(\lambda\) là bước sóng ánh sáng.
- \(m\) là bậc của vân nhiễu xạ (m = 0, ±1, ±2,...).
Khi \(m = 0\), ta có vân sáng trung tâm lớn nhất. Các vân sáng và tối xuất hiện theo khoảng cách xác định, tạo ra hình ảnh đặc trưng của nhiễu xạ. Hiện tượng này có ứng dụng quan trọng trong các thiết bị quang học và nghiên cứu khoa học.
2. Phương Trình Tính Toán Nhiễu Xạ
Trong hiện tượng nhiễu xạ qua 1 khe hẹp, việc tính toán vị trí các vân sáng và vân tối trên màn hứng là rất quan trọng để hiểu rõ cách ánh sáng phân bố sau khi đi qua khe. Dưới đây là các phương trình cơ bản sử dụng trong tính toán nhiễu xạ:
- Phương trình chính của nhiễu xạ: Để xác định vị trí của các vân sáng trên màn hứng, ta sử dụng phương trình:
Trong đó:
- \(a\) là chiều rộng của khe hẹp.
- \(\theta\) là góc nhiễu xạ tính từ trục trung tâm.
- \(\lambda\) là bước sóng của ánh sáng.
- \(m\) là bậc của vân sáng (m = 0, ±1, ±2,...).
Vị trí của các vân tối có thể được xác định bởi công thức:
Trong đó, các thông số \(a\), \(\theta\), \(\lambda\) tương tự như ở trên, nhưng giá trị \(m\) ở đây là số nguyên dương.
- Tính toán khoảng cách giữa các vân: Để tính khoảng cách giữa hai vân sáng liên tiếp (hoặc hai vân tối liên tiếp), ta sử dụng công thức:
Trong đó:
- \(\Delta y\) là khoảng cách giữa hai vân liên tiếp trên màn hứng.
- \(D\) là khoảng cách từ khe hẹp đến màn hứng.
- \(a\) là chiều rộng khe hẹp.
Các phương trình trên là nền tảng cho việc phân tích và mô phỏng hiện tượng nhiễu xạ, giúp ta hiểu rõ hơn về sự phân bố của ánh sáng sau khi đi qua các vật cản nhỏ.

3. Ứng Dụng Hiện Tượng Nhiễu Xạ Trong Đời Sống
Hiện tượng nhiễu xạ qua 1 khe hẹp không chỉ là một khái niệm trong vật lý lý thuyết mà còn có nhiều ứng dụng thực tiễn trong đời sống hàng ngày. Dưới đây là một số ứng dụng nổi bật của hiện tượng này:
- Công nghệ quang học: Hiện tượng nhiễu xạ được ứng dụng trong việc thiết kế các thiết bị quang học như máy quang phổ, nơi nó giúp phân tích và đo lường bước sóng ánh sáng. Các lưới nhiễu xạ được sử dụng để phân tách ánh sáng thành các thành phần phổ, giúp trong nghiên cứu vật liệu và phân tích hóa học.
- Thiết kế ống kính máy ảnh: Nhiễu xạ cũng ảnh hưởng đến khả năng phân giải của ống kính máy ảnh. Bằng cách hiểu rõ hiện tượng nhiễu xạ, các nhà sản xuất có thể tối ưu hóa thiết kế ống kính để giảm thiểu hiện tượng này, đảm bảo hình ảnh sắc nét hơn.
- Kiểm tra và đánh giá vật liệu: Hiện tượng nhiễu xạ X-ray (tia X) được sử dụng để phân tích cấu trúc tinh thể của vật liệu. Kỹ thuật này giúp xác định cấu trúc bên trong của các vật liệu phức tạp, từ đó đánh giá chất lượng và ứng dụng của chúng trong các ngành công nghiệp khác nhau.
- Truyền thông và mạng: Nhiễu xạ cũng đóng vai trò trong việc thiết kế và triển khai các hệ thống truyền thông, đặc biệt là trong việc truyền tải sóng vô tuyến. Hiện tượng nhiễu xạ giúp sóng vô tuyến có thể uốn cong quanh các chướng ngại vật, đảm bảo sóng tín hiệu được truyền tải một cách hiệu quả hơn trong môi trường đô thị.
- Ứng dụng trong y học: Nhiễu xạ tia X cũng là nền tảng của kỹ thuật chụp cắt lớp vi tính (CT scan), giúp tạo ra hình ảnh chi tiết của cơ thể con người mà không cần phải phẫu thuật. Điều này hỗ trợ rất nhiều trong việc chẩn đoán và điều trị bệnh.
Như vậy, từ những ứng dụng trên, có thể thấy rằng hiện tượng nhiễu xạ qua 1 khe hẹp có tác động rộng lớn và quan trọng trong nhiều lĩnh vực khoa học và công nghệ.

4. Thí Nghiệm Về Nhiễu Xạ Qua 1 Khe Hẹp
Thí nghiệm nhiễu xạ qua 1 khe hẹp là một trong những thí nghiệm cơ bản và quan trọng để minh họa rõ ràng hiện tượng nhiễu xạ ánh sáng. Thông qua thí nghiệm này, chúng ta có thể quan sát được các vân nhiễu xạ hình thành khi sóng ánh sáng đi qua một khe hẹp và lan tỏa ra phía sau. Các bước thực hiện thí nghiệm như sau:
- Chuẩn bị dụng cụ: Chuẩn bị một nguồn sáng đơn sắc (thường là laser), một tấm chắn có khe hẹp với độ rộng \(a\), và một màn chiếu để quan sát vân nhiễu xạ.
- Thiết lập thí nghiệm: Đặt nguồn sáng laser sao cho chùm tia sáng chiếu thẳng vào khe hẹp trên tấm chắn. Màn chiếu đặt phía sau tấm chắn ở khoảng cách đủ xa để quan sát rõ vân nhiễu xạ.
- Tiến hành thí nghiệm: Khi ánh sáng laser đi qua khe hẹp, nó sẽ tạo ra các vân sáng tối xen kẽ trên màn chiếu, gọi là các vân nhiễu xạ. Quan sát và đo đạc khoảng cách giữa các vân sáng để xác định tính chất của sóng ánh sáng.
- Tính toán và phân tích: Sử dụng công thức nhiễu xạ qua khe hẹp:
\[
\sin \theta = \frac{m \lambda}{a}
\]
Trong đó:
- \(\theta\) là góc nhiễu xạ của vân sáng thứ \(m\)
- \(\lambda\) là bước sóng của ánh sáng
- \(a\) là độ rộng của khe hẹp
- \(m\) là bậc của vân sáng (m = 0, ±1, ±2, ...)
- Kết luận: Kết quả thí nghiệm sẽ cho thấy rõ ràng sự hình thành của các vân sáng tối, minh họa sự uốn cong và giao thoa của sóng ánh sáng khi gặp chướng ngại vật (khe hẹp). Đây là một bằng chứng thực nghiệm về bản chất sóng của ánh sáng.
Thí nghiệm này không chỉ giúp hiểu rõ hơn về hiện tượng nhiễu xạ mà còn là nền tảng cho nhiều ứng dụng trong quang học và vật lý sóng.

5. 10 Dạng Bài Tập Nhiễu Xạ Qua 1 Khe Hẹp Có Lời Giải Hoàn Chỉnh
Dưới đây là 10 dạng bài tập về nhiễu xạ qua 1 khe hẹp, mỗi bài đều kèm theo lời giải chi tiết để giúp bạn nắm vững kiến thức và phương pháp giải các bài toán nhiễu xạ:
- Bài tập 1: Tính góc nhiễu xạ của vân sáng bậc nhất khi biết độ rộng khe hẹp và bước sóng ánh sáng sử dụng công thức \(\sin \theta = \frac{\lambda}{a}\).
- Bài tập 2: Xác định khoảng cách giữa các vân sáng liên tiếp trên màn chiếu khi biết khoảng cách từ khe hẹp đến màn chiếu và bước sóng ánh sáng.
- Bài tập 3: Tính độ rộng khe hẹp khi biết góc nhiễu xạ của vân sáng bậc hai và bước sóng ánh sáng sử dụng công thức \(\sin \theta = \frac{2\lambda}{a}\).
- Bài tập 4: Xác định bước sóng ánh sáng khi biết độ rộng khe hẹp và góc nhiễu xạ của vân sáng bậc nhất.
- Bài tập 5: Tìm số vân sáng trên màn chiếu trong khoảng góc nhiễu xạ đã cho khi biết độ rộng khe hẹp và bước sóng ánh sáng.
- Bài tập 6: Tính khoảng cách giữa các vân tối liên tiếp khi biết độ rộng khe hẹp, khoảng cách từ khe đến màn và bước sóng ánh sáng.
- Bài tập 7: Xác định vị trí vân sáng thứ ba trên màn chiếu khi biết bước sóng ánh sáng và khoảng cách từ khe hẹp đến màn.
- Bài tập 8: Tính độ rộng khe hẹp cần thiết để quan sát được một số lượng vân sáng nhất định trên màn chiếu.
- Bài tập 9: Xác định bước sóng ánh sáng khi biết số vân sáng quan sát được và khoảng cách giữa các vân trên màn chiếu.
- Bài tập 10: Giải quyết bài toán liên quan đến việc thay đổi một trong các thông số như bước sóng ánh sáng hoặc độ rộng khe hẹp để làm thay đổi số vân sáng trên màn chiếu.
Mỗi bài tập trên đều có lời giải hoàn chỉnh, giúp bạn hiểu rõ và áp dụng các công thức tính toán nhiễu xạ qua 1 khe hẹp vào thực tế.
XEM THÊM:
Dạng Bài Tập 1: Tính Toán Vị Trí Vân Sáng Trung Tâm
Vân sáng trung tâm là vị trí có cường độ sáng lớn nhất trong mô hình nhiễu xạ qua 1 khe hẹp, nơi các tia sáng từ các điểm khác nhau trên khe gặp nhau đồng pha. Để tính toán vị trí vân sáng trung tâm, ta cần sử dụng các công thức toán học liên quan đến nhiễu xạ ánh sáng.
- Bước 1: Xác định các thông số cơ bản:
- Bước sóng ánh sáng: \(\lambda\)
- Độ rộng khe hẹp: \(a\)
- Khoảng cách từ khe hẹp đến màn chiếu: \(L\)
- Bước 2: Sử dụng công thức tính vị trí vân sáng trung tâm:
Vị trí vân sáng trung tâm được xác định tại vị trí góc \(\theta = 0\), và khoảng cách từ khe đến vị trí này trên màn chiếu được tính bằng công thức:
\[
y_0 = L \cdot \tan(0) = 0
\]
Do đó, vân sáng trung tâm nằm ngay trên đường thẳng kéo dài từ khe hẹp vuông góc với màn chiếu. - Bước 3: Xác định các điều kiện để có vân sáng trung tâm:
Vân sáng trung tâm xuất hiện khi điều kiện nhiễu xạ thỏa mãn:
\[
a \sin(\theta) = m\lambda \quad \text{với} \quad m = 0
\]
Trong đó, \(m\) là bậc của vân sáng. Đối với vân sáng trung tâm, \(m = 0\), nên \(\theta = 0\). - Bước 4: Kết luận về vị trí vân sáng trung tâm:
Vân sáng trung tâm luôn xuất hiện tại điểm giữa của màn chiếu, nơi góc \(\theta = 0\), tương ứng với khoảng cách \(y_0 = 0\) trên màn.

Dạng Bài Tập 2: Xác Định Vị Trí Các Vân Sáng Phụ
Để xác định vị trí các vân sáng phụ trong hiện tượng nhiễu xạ qua 1 khe hẹp, ta cần dựa vào công thức nhiễu xạ cho các vân sáng phụ. Các vân sáng phụ xuất hiện tại các vị trí mà điều kiện nhiễu xạ thỏa mãn:
Trong đó:
- \(d\): Độ rộng của khe hẹp.
- \(\theta\): Góc nhiễu xạ tính từ đường thẳng trung tâm.
- \(\lambda\): Bước sóng ánh sáng sử dụng.
- \(m\): Thứ tự của vân sáng phụ (với \(m = 0\) là vân sáng trung tâm).
Hướng dẫn giải bài tập xác định vị trí các vân sáng phụ
-
Bước 1: Xác định các thông số cho trước trong bài toán, bao gồm độ rộng khe \(d\), bước sóng ánh sáng \(\lambda\), và vị trí của các vân sáng cần tìm (thứ tự \(m\)).
-
Bước 2: Sử dụng công thức nhiễu xạ để tính góc \(\theta\) cho các vân sáng phụ:
\[ \sin(\theta) = \frac{m \lambda}{d} \]Giải phương trình trên để tìm giá trị của \(\theta\) tương ứng với các giá trị \(m\) khác nhau.
-
Bước 3: Đối với các giá trị \(m\) cho trước, tính giá trị \(\theta\) để xác định góc nhiễu xạ cho từng vân sáng phụ.
-
Bước 4: Vẽ biểu đồ hoặc hình minh họa để xác định các vị trí vân sáng phụ trên màn quan sát.
Ví dụ minh họa
Giả sử có khe hẹp với độ rộng \(d = 0.5 \, mm\) và ánh sáng có bước sóng \(\lambda = 600 \, nm\). Tìm vị trí các vân sáng phụ thứ nhất (m = ±1).
- Bước 1: Thông số cho trước: \(d = 0.5 \, mm = 0.5 \times 10^{-3} \, m\), \(\lambda = 600 \, nm = 600 \times 10^{-9} \, m\), \(m = \pm 1\).
- Bước 2: Tính \(\sin(\theta)\): \[ \sin(\theta) = \frac{m \lambda}{d} = \frac{\pm 1 \times 600 \times 10^{-9}}{0.5 \times 10^{-3}} \] \[ \sin(\theta) = \pm 0.0012 \]
- Bước 3: Tính góc \(\theta\) từ \(\sin(\theta)\): \[ \theta = \arcsin(0.0012) \approx 0.07^\circ \]
- Bước 4: Các vân sáng phụ xuất hiện tại góc \(\theta \approx \pm 0.07^\circ\) so với đường trung tâm.
Như vậy, ta đã xác định được vị trí các vân sáng phụ bằng cách sử dụng công thức nhiễu xạ và thực hiện các bước tính toán đơn giản.

Dạng Bài Tập 3: Tính Toán Góc Nhiễu Xạ Tối Thiểu
Trong hiện tượng nhiễu xạ qua khe hẹp, góc nhiễu xạ tối thiểu là góc nhỏ nhất tại đó cường độ ánh sáng đạt cực tiểu. Để tính toán góc nhiễu xạ tối thiểu, chúng ta cần sử dụng công thức liên quan đến bước sóng ánh sáng \(\lambda\) và kích thước khe hẹp \(a\).
1. Công thức tính toán:
- Công thức tính góc nhiễu xạ tối thiểu \( \theta \) là:
\[
\sin(\theta) = \frac{m \cdot \lambda}{a}
\]
- Trong đó:
- \( \theta \): Góc nhiễu xạ tối thiểu cần tính
- \( m \): Bậc nhiễu xạ (thường là số nguyên dương, \(m = 1, 2, 3, \ldots\))
- \( \lambda \): Bước sóng của ánh sáng (đơn vị: mét)
- \( a \): Độ rộng của khe hẹp (đơn vị: mét)
2. Ví dụ tính toán:
- Giả sử ánh sáng có bước sóng \(\lambda = 600 \, \text{nm} = 600 \times 10^{-9} \, \text{m}\), và khe hẹp có độ rộng \(a = 0.1 \, \text{mm} = 0.1 \times 10^{-3} \, \text{m}\).
- Ta cần tính góc nhiễu xạ tối thiểu cho bậc nhiễu xạ đầu tiên \(m = 1\).
- Sử dụng công thức trên:
\[
\sin(\theta) = \frac{1 \times 600 \times 10^{-9}}{0.1 \times 10^{-3}} = 0.006
\]
- Sử dụng máy tính để tìm góc \( \theta \):
\[
\theta = \arcsin(0.006) \approx 0.343^\circ
\]
3. Kết luận:
- Góc nhiễu xạ tối thiểu cho ánh sáng có bước sóng 600 nm qua khe hẹp có độ rộng 0.1 mm là khoảng \(0.343^\circ\).
- Các bài tập tương tự có thể được thực hiện với các giá trị khác của bước sóng và độ rộng khe để tính toán góc nhiễu xạ tối thiểu cho các bậc nhiễu xạ khác nhau.
Hy vọng rằng qua ví dụ này, bạn đã hiểu rõ hơn về cách tính toán góc nhiễu xạ tối thiểu và các yếu tố ảnh hưởng đến nó trong hiện tượng nhiễu xạ qua khe hẹp.
Dạng Bài Tập 4: Tính Độ Rộng Vân Sáng Trung Tâm
Trong hiện tượng nhiễu xạ ánh sáng qua một khe hẹp, vân sáng trung tâm là khu vực sáng nhất trên màn quan sát và có kích thước lớn nhất. Để tính độ rộng của vân sáng trung tâm, chúng ta cần hiểu các yếu tố ảnh hưởng như bước sóng ánh sáng, bề rộng khe hẹp và khoảng cách từ khe đến màn quan sát.
Công thức tính độ rộng vân sáng trung tâm
Độ rộng của vân sáng trung tâm có thể được tính bằng công thức:
trong đó:
- \(w\) là độ rộng của vân sáng trung tâm.
- \(\lambda\) là bước sóng của ánh sáng (đơn vị: mét).
- \(D\) là khoảng cách từ khe hẹp đến màn quan sát (đơn vị: mét).
- \(a\) là bề rộng của khe hẹp (đơn vị: mét).
Ví dụ minh họa
Giả sử có một khe hẹp với bề rộng \(a = 0,02 \, mm = 2 \times 10^{-5} \, m\), chiếu ánh sáng có bước sóng \(\lambda = 480 \, nm = 4,8 \times 10^{-7} \, m\) qua khe. Màn quan sát đặt cách khe một khoảng \(D = 0,5 \, m\). Hãy tính độ rộng của vân sáng trung tâm.
Áp dụng công thức, chúng ta có:
Vậy, độ rộng của vân sáng trung tâm là 4,8 cm.
Các bước giải bài tập
- Xác định các đại lượng đã biết: bước sóng \(\lambda\), khoảng cách \(D\), và bề rộng khe \(a\).
- Sử dụng công thức \(w = \frac{2 \lambda D}{a}\) để tính độ rộng vân sáng trung tâm.
- Thay các giá trị đã biết vào công thức và tính toán để tìm kết quả.
Việc hiểu rõ các yếu tố và công thức này giúp ta dễ dàng hơn trong việc giải quyết các bài tập liên quan đến nhiễu xạ qua khe hẹp và tính toán chính xác các thông số cần thiết.

Dạng Bài Tập 5: Ảnh Hưởng Của Bước Sóng Đến Hình Dạng Nhiễu Xạ
Hiện tượng nhiễu xạ qua khe hẹp xảy ra khi sóng ánh sáng đi qua một khe có kích thước nhỏ hơn bước sóng của nó. Điều này làm cho sóng lan tỏa ra và tạo ra các vân nhiễu xạ trên màn quan sát. Hình dạng và vị trí của các vân sáng và tối phụ thuộc vào bước sóng của ánh sáng và kích thước khe hẹp.
- Bước sóng càng dài: Các vân nhiễu xạ càng rộng hơn, khoảng cách giữa các vân sáng liên tiếp càng lớn. Điều này xảy ra do góc nhiễu xạ θ tăng khi bước sóng λ tăng, theo công thức: \[ \sin \theta = \frac{m \lambda}{b} \] với m là bậc của vân và b là chiều rộng khe.
- Bước sóng ngắn: Các vân nhiễu xạ sẽ hẹp lại và gần nhau hơn. Khi λ giảm, các vân sáng gần nhau hơn, làm cho mô hình nhiễu xạ trở nên chi tiết hơn.
Để hiểu rõ hơn về ảnh hưởng của bước sóng đến hình dạng nhiễu xạ, hãy xem xét các trường hợp cụ thể:
- Trường hợp bước sóng lớn: Với bước sóng λ lớn, vân sáng trung tâm (vân sáng bậc 0) sẽ rất rộng, và các vân sáng, vân tối tiếp theo sẽ xuất hiện ở vị trí xa hơn. Công thức tính vị trí các vân sáng bậc m là: \[ y_m = \frac{m \lambda L}{b} \] với L là khoảng cách từ khe hẹp đến màn quan sát.
- Trường hợp bước sóng nhỏ: Khi λ nhỏ, các vân sáng và tối sẽ xuất hiện gần nhau hơn, làm cho mô hình nhiễu xạ trở nên phức tạp với nhiều vân sáng và tối xuất hiện liên tục trên màn.
Hãy thực hành một số bài tập sau để làm rõ hơn về ảnh hưởng của bước sóng đến hình dạng nhiễu xạ:
| Bài tập | Yêu cầu |
|---|---|
| Bài tập 1 | Tính khoảng cách giữa hai vân sáng liên tiếp khi ánh sáng có bước sóng 600 nm đi qua khe hẹp có chiều rộng 0,2 mm và màn cách khe 2 m. |
| Bài tập 2 | Xác định số vân sáng và tối quan sát được trên màn khi sử dụng ánh sáng bước sóng 450 nm với các điều kiện tương tự như bài tập 1. |
Qua các bài tập này, chúng ta có thể thấy rõ sự thay đổi của hình dạng nhiễu xạ khi thay đổi bước sóng ánh sáng. Sử dụng các công thức tính toán như trên, bạn có thể xác định được vị trí và khoảng cách giữa các vân nhiễu xạ trong nhiều trường hợp khác nhau.
Dạng Bài Tập 6: Phân Tích Thí Nghiệm Nhiễu Xạ Qua Khe Hẹp
Trong bài tập này, chúng ta sẽ phân tích chi tiết thí nghiệm nhiễu xạ ánh sáng qua khe hẹp để hiểu rõ hơn về cách mà hiện tượng nhiễu xạ xảy ra cũng như cách tính toán các thông số liên quan.
1. Thiết lập thí nghiệm
- Một nguồn sáng đơn sắc, thường là tia laser, được chiếu thẳng vào một khe hẹp có chiều rộng \(a\).
- Màn quan sát đặt cách khe một khoảng cách \(L\) để thu được hình ảnh nhiễu xạ.
2. Hiện tượng nhiễu xạ
Khi ánh sáng đi qua khe hẹp, nó sẽ bị uốn cong và tạo ra một mô hình nhiễu xạ với các cực đại và cực tiểu trên màn quan sát. Các cực đại và cực tiểu này được xác định bởi công thức:
- Vị trí của cực đại: \[a \sin(\theta_m) = m \lambda\]
- Vị trí của cực tiểu: \[a \sin(\theta_n) = (n + 0.5) \lambda\]
Với:
- \(a\): Chiều rộng của khe
- \(\lambda\): Bước sóng của ánh sáng
- \(\theta_m, \theta_n\): Góc lệch tương ứng với cực đại bậc \(m\) và cực tiểu bậc \(n\)
3. Đo đạc và tính toán
Để tính toán được các góc nhiễu xạ, chúng ta có thể sử dụng công thức:
- \(\sin \theta_m = \frac{m \lambda}{a}\)
Trong đó:
- \(m\) là thứ tự của cực đại (m = 0, 1, 2,...)
Các góc nhiễu xạ được đo bằng cách sử dụng các dụng cụ đo góc trên màn quan sát.
4. Phân tích kết quả thí nghiệm
Kết quả của thí nghiệm sẽ cho ta biết sự phụ thuộc của hình ảnh nhiễu xạ vào các thông số như chiều rộng của khe và bước sóng của ánh sáng. Bằng cách thay đổi các tham số này và quan sát sự thay đổi của mô hình nhiễu xạ, chúng ta có thể rút ra những kết luận quan trọng về tính chất của nhiễu xạ.
5. Kết luận
Thông qua thí nghiệm nhiễu xạ qua khe hẹp, chúng ta có thể hiểu rõ hơn về sự tương tác giữa ánh sáng và vật cản. Đây là một ví dụ điển hình minh họa cho nguyên lý nhiễu xạ, một hiện tượng quan trọng trong quang học và vật lý sóng.
Dạng Bài Tập 7: So Sánh Nhiễu Xạ Qua Khe Hẹp Và Nhiễu Xạ Qua Cách Tử
Nhiễu xạ ánh sáng là hiện tượng ánh sáng uốn cong khi đi qua các vật cản hoặc khe hẹp. Đây là một hiện tượng quan trọng trong vật lý, đặc biệt trong lĩnh vực quang học. Trong bài học này, chúng ta sẽ so sánh hai trường hợp nhiễu xạ khác nhau: nhiễu xạ qua khe hẹp và nhiễu xạ qua cách tử.
- Nhiễu xạ qua khe hẹp: Khi ánh sáng đi qua một khe hẹp, nó sẽ uốn cong ra hai bên, tạo ra các vân sáng và tối trên màn hình phía sau. Các vân này được gọi là các vân nhiễu xạ.
- Nhiễu xạ qua cách tử: Khi ánh sáng đi qua một cách tử, một loạt các khe hẹp, nó sẽ tạo ra một mô hình nhiễu xạ phức tạp hơn với nhiều vân sáng và tối. Điều này xảy ra do sự giao thoa của nhiều sóng ánh sáng đi qua các khe khác nhau.
Để hiểu rõ hơn, chúng ta cần phân tích các yếu tố ảnh hưởng đến mô hình nhiễu xạ trong cả hai trường hợp:
- Khoảng cách giữa các khe: Đối với nhiễu xạ qua khe hẹp, chỉ có một khe, do đó không có sự tương tác giữa các sóng qua nhiều khe. Trong khi đó, đối với cách tử, khoảng cách giữa các khe ảnh hưởng trực tiếp đến vị trí và độ sáng của các vân nhiễu xạ.
- Độ rộng của khe: Độ rộng của khe hẹp quyết định góc nhiễu xạ và khoảng cách giữa các vân. Càng hẹp khe, các vân nhiễu xạ sẽ càng rộng và ngược lại. Đối với cách tử, độ rộng của mỗi khe cũng có vai trò quan trọng nhưng ít ảnh hưởng hơn khoảng cách giữa các khe.
- Chiều dài sóng của ánh sáng: Chiều dài sóng của ánh sáng sử dụng cũng ảnh hưởng đến mô hình nhiễu xạ. Với ánh sáng có bước sóng dài hơn, các vân nhiễu xạ sẽ rộng hơn. Điều này áp dụng cho cả khe hẹp và cách tử.
Sự khác biệt chính giữa hai hiện tượng nhiễu xạ này là do số lượng các khe tham gia vào quá trình nhiễu xạ và cách mà chúng ảnh hưởng đến mô hình vân sáng và tối. Bằng cách nắm rõ các yếu tố này, chúng ta có thể hiểu sâu hơn về bản chất của nhiễu xạ và ứng dụng của nó trong thực tế.
Mô hình toán học để biểu diễn nhiễu xạ qua khe hẹp và cách tử như sau:
- Nhiễu xạ qua khe hẹp: Công thức tính góc nhiễu xạ cho vân tối thứ \(n\) là:
\[
a \sin \theta = n\lambda
\]
Trong đó:
- \(a\): Độ rộng của khe.
- \(\theta\): Góc nhiễu xạ.
- \(n\): Bậc của vân tối (n = ±1, ±2, ...).
- \(\lambda\): Chiều dài sóng của ánh sáng.
- Nhiễu xạ qua cách tử: Công thức tính góc nhiễu xạ cho vân sáng thứ \(m\) là:
\[
d \sin \theta = m\lambda
\]
Trong đó:
- \(d\): Khoảng cách giữa các khe của cách tử.
- \(\theta\): Góc nhiễu xạ.
- \(m\): Bậc của vân sáng (m = 0, ±1, ±2, ...).
- \(\lambda\): Chiều dài sóng của ánh sáng.
Qua đó, chúng ta thấy rằng trong nhiễu xạ qua cách tử, góc nhiễu xạ không chỉ phụ thuộc vào chiều dài sóng mà còn phụ thuộc nhiều vào khoảng cách giữa các khe, tạo nên mô hình nhiễu xạ phức tạp và nhiều màu sắc hơn so với nhiễu xạ qua khe hẹp.

Dạng Bài Tập 8: Tính Cường Độ Sáng Tại Các Vị Trí Khác Nhau
Trong bài tập này, chúng ta sẽ tính cường độ sáng của ánh sáng tại các vị trí khác nhau khi xảy ra hiện tượng nhiễu xạ qua một khe hẹp. Để tính toán cường độ sáng, ta cần sử dụng công thức của nhiễu xạ ánh sáng qua một khe hẹp.
Giả sử ánh sáng đơn sắc có bước sóng \(\lambda\) đi qua một khe hẹp có độ rộng \(a\) và tạo ra hiện tượng nhiễu xạ trên màn ảnh. Cường độ sáng tại một điểm trên màn được cho bởi công thức:
trong đó:
- \(I(\theta)\): Cường độ sáng tại góc nhiễu xạ \(\theta\)
- \(I_0\): Cường độ sáng tại tâm nhiễu xạ (vân sáng trung tâm)
- \(\beta = \frac{\pi a \sin(\theta)}{\lambda}\): Tham số liên quan đến góc nhiễu xạ \(\theta\), độ rộng khe \(a\), và bước sóng ánh sáng \(\lambda\)
Để tính cường độ sáng tại các vị trí khác nhau trên màn, ta thực hiện các bước sau:
- Xác định các tham số ban đầu: bước sóng \(\lambda\), độ rộng khe \(a\), và cường độ sáng tại tâm nhiễu xạ \(I_0\).
- Tính giá trị của \(\beta\) cho từng góc nhiễu xạ \(\theta\) mà ta quan tâm.
- Sử dụng công thức tính cường độ sáng \(I(\theta)\) để tìm cường độ tại các vị trí khác nhau.
Ví dụ: Nếu ta biết độ rộng khe \(a = 0.5 \, mm\), bước sóng \(\lambda = 600 \, nm\), và cường độ sáng tại tâm \(I_0 = 100 \, mW/m^2\), chúng ta có thể tính cường độ sáng tại các góc khác nhau như sau:
| Góc nhiễu xạ (\(\theta\)) | Giá trị \(\beta\) | Cường độ sáng \(I(\theta)\) (mW/m2) |
|---|---|---|
| 0° | 0 | 100 |
| 10° | \(\frac{\pi \times 0.5 \times \sin(10^\circ)}{600 \times 10^{-9}}\) | \(I_0 \left( \frac{\sin(\beta)}{\beta} \right)^2\) |
| 20° | \(\frac{\pi \times 0.5 \times \sin(20^\circ)}{600 \times 10^{-9}}\) | \(I_0 \left( \frac{\sin(\beta)}{\beta} \right)^2\) |
Như vậy, bằng cách sử dụng công thức trên, chúng ta có thể tính được cường độ sáng tại các vị trí khác nhau trên màn nhiễu xạ, giúp phân tích rõ hơn về hình dạng và đặc tính của các vân nhiễu xạ.
Dạng Bài Tập 9: Xác Định Khoảng Cách Giữa Các Vân Sáng
Trong hiện tượng nhiễu xạ qua một khe hẹp, việc xác định khoảng cách giữa các vân sáng trên màn hình là một phần quan trọng của các bài tập quang học. Dưới đây là các bước cơ bản để giải quyết dạng bài tập này.
-
Bước 1: Xác định công thức liên quan
Công thức xác định khoảng cách giữa hai vân sáng liên tiếp trong hiện tượng nhiễu xạ qua khe hẹp là:
\[ \Delta y = \frac{\lambda L}{a} \]Trong đó:
- \(\Delta y\): Khoảng cách giữa hai vân sáng liên tiếp
- \(\lambda\): Bước sóng của ánh sáng sử dụng
- \(L\): Khoảng cách từ khe đến màn
- \(a\): Độ rộng của khe hẹp
-
Bước 2: Xác định các giá trị đã biết
Trước khi tính toán, bạn cần xác định các giá trị đã cho trong đề bài, bao gồm:
- Bước sóng ánh sáng \(\lambda\)
- Khoảng cách từ khe đến màn \(L\)
- Độ rộng của khe \(a\)
-
Bước 3: Thay các giá trị vào công thức
Sau khi đã có đầy đủ các giá trị, thay chúng vào công thức:
\[ \Delta y = \frac{\lambda L}{a} \]Đảm bảo rằng tất cả các đơn vị đo lường đều thống nhất trước khi tính toán.
-
Bước 4: Thực hiện phép tính
Sử dụng máy tính hoặc tính toán thủ công để tìm ra giá trị của \(\Delta y\). Đây là khoảng cách giữa hai vân sáng liên tiếp mà bạn cần tìm.
-
Bước 5: Kiểm tra kết quả
Đảm bảo rằng kết quả tính toán hợp lý và phù hợp với các thông tin đã cho trong bài tập. Nếu cần thiết, thực hiện các phép tính kiểm tra hoặc so sánh với kết quả lý thuyết để đảm bảo tính chính xác.
Qua các bước trên, bạn có thể dễ dàng xác định khoảng cách giữa các vân sáng trong hiện tượng nhiễu xạ qua một khe hẹp. Hãy luyện tập nhiều bài tập để nắm vững cách giải và cải thiện kỹ năng tính toán của mình.
Dạng Bài Tập 10: Ứng Dụng Hiện Tượng Nhiễu Xạ Trong Thực Tiễn
Hiện tượng nhiễu xạ qua khe hẹp là một hiện tượng quan trọng trong quang học, giúp chúng ta hiểu rõ hơn về tính chất của sóng ánh sáng. Trong thực tiễn, hiện tượng này có nhiều ứng dụng quan trọng như sau:
- Thiết bị y tế: Nhiễu xạ ánh sáng được ứng dụng trong các thiết bị y tế, như máy chụp X-quang và máy quang phổ, để phân tích cấu trúc bên trong cơ thể con người và xác định thành phần của các chất trong cơ thể.
- Kiểm tra chất lượng vật liệu: Kỹ thuật nhiễu xạ X-ray (tia X) được sử dụng để phân tích cấu trúc tinh thể của vật liệu, giúp kiểm tra chất lượng và độ tinh khiết của chúng. Đây là một công cụ quan trọng trong nghiên cứu vật liệu và ngành công nghiệp sản xuất.
- Thiết kế thiết bị quang học: Hiểu rõ hiện tượng nhiễu xạ giúp các nhà khoa học và kỹ sư thiết kế các thiết bị quang học, như kính thiên văn và kính hiển vi, với độ chính xác cao hơn.
- Công nghệ thông tin: Nhiễu xạ ánh sáng được ứng dụng trong công nghệ chế tạo các thiết bị lưu trữ thông tin quang học như đĩa CD, DVD và Blu-ray, nơi mà các rãnh nhiễu xạ giúp lưu trữ và đọc dữ liệu với mật độ cao.
- Nghiên cứu khoa học: Trong nghiên cứu khoa học, nhiễu xạ được sử dụng để phân tích cấu trúc phân tử của các chất, giúp hiểu rõ hơn về cấu trúc và tính chất của chúng.
Trong các thí nghiệm thực tế, nhiễu xạ qua khe hẹp giúp kiểm tra sự đồng nhất của các mẫu vật liệu hoặc phân tích các mẫu sinh học với độ chính xác cao. Ngoài ra, hiện tượng này còn được ứng dụng trong các nghiên cứu về thiên văn học, như phân tích ánh sáng từ các ngôi sao và thiên hà để xác định thành phần hóa học và nhiệt độ của chúng.
Ví dụ, khi một tia sáng đơn sắc đi qua một khe hẹp, nó sẽ tạo ra một mô hình nhiễu xạ trên màn. Khoảng cách giữa các vân sáng có thể được tính toán dựa vào công thức nhiễu xạ:
trong đó:
- \(a\) là độ rộng của khe hẹp.
- \(\theta\) là góc tạo bởi tia sáng và đường thẳng vuông góc với khe.
- \(m\) là bậc của vân nhiễu xạ (m = 0, ±1, ±2, ...).
- \(\lambda\) là bước sóng của ánh sáng.
Nhờ ứng dụng của hiện tượng nhiễu xạ qua khe hẹp, chúng ta có thể tiến hành các nghiên cứu và phát triển các công nghệ mới trong nhiều lĩnh vực khác nhau, từ y tế, khoa học vật liệu đến công nghệ thông tin và thiên văn học.