Nhiễu Xạ Tinh Thể: Nguyên Lý, Ứng Dụng Và Phân Tích Khoa Học

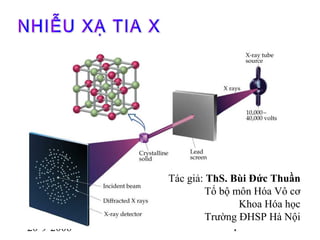
Nhiễu xạ tinh thể là một hiện tượng vật lý quan trọng trong nghiên cứu và phân tích cấu trúc tinh thể của vật liệu. Thông qua nhiễu xạ tia X (X-ray Diffraction - XRD), các nhà khoa học có thể xác định được thông tin chi tiết về cấu trúc tinh thể, các pha, và độ tinh khiết của mẫu vật liệu.

Cơ Chế Nhiễu Xạ Tinh Thể

Khi chùm tia X chiếu vào tinh thể, các nguyên tử trong mạng tinh thể đóng vai trò như cách tử nhiễu xạ, gây ra hiện tượng giao thoa, tạo nên các đỉnh nhiễu xạ. Mô hình nhiễu xạ thu được phụ thuộc vào cách sắp xếp nguyên tử trong mạng tinh thể và có thể so sánh với các cơ sở dữ liệu để xác định loại vật liệu.

• Cấu trúc tinh thể: Các nguyên tử hoặc phân tử được sắp xếp tuần hoàn trong không gian.
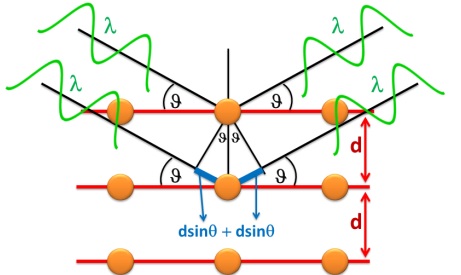
• Định luật Bragg: Phương trình Bragg mô tả mối quan hệ giữa góc nhiễu xạ và khoảng cách giữa các mặt phẳng nguyên tử.

Ứng Dụng Của Phương Pháp Nhiễu Xạ Tia X

• Xác định tính chất của tinh thể trong các vật liệu chưa biết, như khoáng chất và hợp chất vô cơ.
• Đo đạc độ tinh khiết và cấu trúc của các mẫu vật liệu.
• Phân tích các thành phần và định lượng khoáng chất trong mẫu.

Kết Luận

Phương pháp nhiễu xạ tia X đóng vai trò thiết yếu trong khoa học vật liệu, địa chất, và sinh học, giúp các nhà nghiên cứu hiểu rõ hơn về cấu trúc và tính chất của các vật liệu tinh thể.

• Giới Thiệu Về Nhiễu Xạ Tinh Thể

• Nguyên Lý Hoạt Động Của Nhiễu Xạ Tinh Thể

• Phân Tích Và Ứng Dụng Kỹ Thuật Nhiễu Xạ Tinh Thể

• Các Dạng Máy XRD Phổ Biến Trong Nhiễu Xạ Tinh Thể

• Các Phương Pháp Xử Lý Dữ Liệu Trong Nghiên Cứu Nhiễu Xạ Tinh Thể

• Công Nghệ Mới Trong Phân Tích Tinh Thể Học Qua Nhiễu Xạ

• Những Khó Khăn Và Thách Thức Khi Sử Dụng Kỹ Thuật Nhiễu Xạ

• Xác Định Cấu Trúc Vật Liệu Bằng Nhiễu Xạ Tinh Thể

1. Bài tập 1: Tính toán khoảng cách giữa các mặt phẳng tinh thể dựa trên công thức nhiễu xạ Bragg \[n\lambda = 2d\sin\theta\]. Cho biết bước sóng \(\lambda\) và góc \(\theta\), tìm khoảng cách \(d\).

2. Bài tập 2: Phân tích cấu trúc tinh thể từ phổ nhiễu xạ thu được bằng máy XRD. Xác định các góc nhiễu xạ và tính chỉ số Miller (hkl).

3. Bài tập 3: Xác định loại tinh thể (lập phương, tứ giác, lục giác) dựa trên dữ liệu nhiễu xạ và mối quan hệ giữa các mặt phẳng tinh thể.

4. Bài tập 4: Tính toán hằng số mạng tinh thể từ kết quả nhiễu xạ và các chỉ số Miller. Áp dụng công thức liên quan đến đơn vị ô mạng cơ bản.

5. Bài tập 5: Tìm hiểu về nhiễu xạ electron và so sánh kết quả với nhiễu xạ tia X trong việc phân tích cấu trúc tinh thể.

6. Bài tập 6: Sử dụng công cụ phần mềm phân tích phổ nhiễu xạ để giải bài toán cấu trúc tinh thể của một mẫu vật liệu cụ thể.

7. Bài tập 7: Phân tích ảnh hưởng của sai số trong việc đo góc \(\theta\) đến kết quả tính toán khoảng cách mặt phẳng tinh thể.

8. Bài tập 8: So sánh nhiễu xạ của các loại vật liệu đơn tinh thể và đa tinh thể. Phân tích các phổ nhiễu xạ tương ứng.

9. Bài tập 9: Tìm hiểu về các ứng dụng thực tiễn của nhiễu xạ tinh thể trong lĩnh vực vật liệu học và dược phẩm.

10. Bài tập 10: Xác định cấu trúc mạng tinh thể và mật độ nguyên tử dựa trên phổ nhiễu xạ của mẫu vật liệu chưa biết.

Trong bài tập này, ta sẽ áp dụng công thức nhiễu xạ Bragg để xác định khoảng cách giữa các mặt phẳng tinh thể trong một tinh thể nhất định. Công thức Bragg được biểu diễn như sau:

Trong đó:

• \(n\) là bậc nhiễu xạ (thường là 1).
• \(\lambda\) là bước sóng của tia X được sử dụng (đơn vị: nanomet).
• \(d\) là khoảng cách giữa các mặt phẳng tinh thể (đơn vị: nanomet).
• \(\theta\) là góc nhiễu xạ (đơn vị: độ).

Giả sử trong một thí nghiệm nhiễu xạ tia X, ta có các giá trị sau:

• Bước sóng của tia X: \(\lambda = 0.154 \, \text{nm}\)
• Góc nhiễu xạ: \(\theta = 30^\circ\)

Yêu cầu: Xác định khoảng cách \(d\) giữa các mặt phẳng tinh thể.

Bước giải quyết:

1. Thay các giá trị đã cho vào công thức Bragg:
\[ d = \frac{n\lambda}{2\sin\theta} \]
2. Với \(n = 1\), \(\lambda = 0.154 \, \text{nm}\) và \(\theta = 30^\circ\), ta có:
\[ d = \frac{1 \times 0.154}{2 \times \sin(30^\circ)} = \frac{0.154}{2 \times 0.5} = \frac{0.154}{1} = 0.154 \, \text{nm} \]
3. Vậy, khoảng cách giữa các mặt phẳng tinh thể là \(d = 0.154 \, \text{nm}\).

Trong bài tập này, chúng ta sẽ sử dụng công thức nhiễu xạ Bragg để tính góc nhiễu xạ \( \theta \) khi đã biết các giá trị của bước sóng tia X và khoảng cách giữa các mặt phẳng tinh thể.

Trong đó:

• \( n \) là bậc nhiễu xạ (thường là 1).
• \( \lambda \) là bước sóng của tia X (đơn vị: nanomet).
• \( d \) là khoảng cách giữa các mặt phẳng tinh thể (đơn vị: nanomet).
• \( \theta \) là góc nhiễu xạ (đơn vị: độ).

Giả sử ta có các dữ liệu sau:

• Bước sóng của tia X: \( \lambda = 0.154 \, \text{nm} \)
• Khoảng cách giữa các mặt phẳng tinh thể: \( d = 0.200 \, \text{nm} \)

Yêu cầu: Tính góc nhiễu xạ \( \theta \).

Bước giải quyết:

1. Thay các giá trị vào công thức Bragg:
\[ \sin\theta = \frac{n\lambda}{2d} \]
2. Với \( n = 1 \), \( \lambda = 0.154 \, \text{nm} \) và \( d = 0.200 \, \text{nm} \), ta có:
\[ \sin\theta = \frac{1 \times 0.154}{2 \times 0.200} = \frac{0.154}{0.400} = 0.385 \]
3. Do đó, góc nhiễu xạ \( \theta \) là:
\[ \theta = \sin^{-1}(0.385) \approx 22.6^\circ \]

Vậy, góc nhiễu xạ \( \theta \) là khoảng 22.6 độ.

Trong bài tập này, chúng ta sẽ sử dụng dữ liệu từ phép đo nhiễu xạ tia X (XRD) để xác định loại cấu trúc tinh thể của một vật liệu. XRD là phương pháp phân tích phổ biến để nghiên cứu cấu trúc tinh thể, thông qua việc phân tích các góc nhiễu xạ và cường độ của các đỉnh (peaks) trong phổ XRD.

Yêu cầu: Xác định cấu trúc tinh thể của mẫu dựa trên các góc và chỉ số mặt phẳng nhiễu xạ \( hkl \).

Các bước giải quyết:

1. Phân tích dữ liệu XRD để xác định các góc nhiễu xạ \( 2\theta \) và các chỉ số mặt phẳng nhiễu xạ \( hkl \).
2. So sánh với các cấu trúc tinh thể phổ biến như lập phương tâm khối (BCC), lập phương tâm diện (FCC), và cấu trúc lục giác (HCP).
3. Sử dụng công thức tính khoảng cách giữa các mặt phẳng \( d_{hkl} \) trong các cấu trúc khác nhau:
\[ d_{hkl} = \frac{a}{\sqrt{h^2 + k^2 + l^2}} \]
4. Với \( a \) là hằng số mạng (đơn vị: nm).
5. So sánh giá trị thực nghiệm với các cấu trúc chuẩn để xác định loại cấu trúc tinh thể.

Ví dụ: Nếu dữ liệu XRD cho thấy các đỉnh tương ứng với chỉ số mặt phẳng \( (110), (200), (211) \) và tương quan với cấu trúc lập phương tâm khối (BCC), thì mẫu có cấu trúc BCC.

Trong bài tập này, chúng ta sẽ phân tích mẫu nhiễu xạ từ các vật liệu đa tinh thể để xác định các đặc trưng cơ bản của cấu trúc tinh thể. Đa tinh thể là các vật liệu bao gồm nhiều hạt tinh thể nhỏ có hướng ngẫu nhiên, do đó mẫu nhiễu xạ từ các vật liệu này có nhiều đỉnh (peaks) phân bố theo các góc khác nhau.

Các bước phân tích:

1. Thu thập dữ liệu nhiễu xạ đa tinh thể thông qua phương pháp XRD.
2. Phân tích các đỉnh nhiễu xạ quan sát được để xác định các chỉ số mặt phẳng \( hkl \) của từng đỉnh.
3. Sử dụng công thức Bragg để tính toán khoảng cách giữa các mặt phẳng trong tinh thể:
\[ n\lambda = 2d_{hkl} \sin \theta \]
4. Với \( \theta \) là góc nhiễu xạ, \( d_{hkl} \) là khoảng cách giữa các mặt phẳng, và \( \lambda \) là bước sóng của tia X.
5. So sánh kết quả phân tích với cấu trúc tinh thể lý thuyết để đưa ra kết luận về loại cấu trúc của mẫu.

Ví dụ: Nếu mẫu cho các đỉnh nhiễu xạ đặc trưng cho cấu trúc lập phương tâm diện (FCC), ta có thể kết luận mẫu có cấu trúc FCC.

Phương trình Bragg là một công cụ quan trọng trong việc phân tích kết quả nhiễu xạ tinh thể, giúp xác định khoảng cách giữa các mặt phẳng nguyên tử trong một tinh thể dựa trên góc nhiễu xạ. Công thức của phương trình Bragg được biểu diễn như sau:

\[n\lambda = 2d\sin\theta\]

Trong đó:

• \(n\): Bậc nhiễu xạ (thường là \(n = 1\))
• \(\lambda\): Bước sóng của tia X sử dụng trong thí nghiệm
• \(d\): Khoảng cách giữa các mặt phẳng tinh thể
• \(\theta\): Góc nhiễu xạ (góc Bragg)

Để áp dụng phương trình Bragg trong tính toán, ta tiến hành theo các bước sau:

1. Bước 1: Xác định góc nhiễu xạ (\(\theta\)): Sử dụng kết quả nhiễu xạ từ thí nghiệm, xác định góc mà các tia X bị lệch khi đi qua tinh thể.
2. Bước 2: Xác định bước sóng tia X (\(\lambda\)): Bước sóng của tia X thường được cung cấp bởi thiết bị nhiễu xạ, ví dụ \(\lambda = 1.54 \, \mathring{A}\) đối với tia X Cu K\(\alpha\).
3. Bước 3: Tính khoảng cách mặt phẳng (\(d\)): Sử dụng phương trình Bragg để tính toán khoảng cách giữa các mặt phẳng trong tinh thể. Với góc \(\theta\) và bước sóng \(\lambda\), ta có thể suy ra \(d\) qua công thức: \[ d = \frac{n\lambda}{2\sin\theta} \]
4. Bước 4: Phân tích kết quả: Sau khi tính toán được khoảng cách \(d\), ta có thể so sánh với các giá trị lý thuyết hoặc sử dụng để xác định loại cấu trúc tinh thể.

Ví dụ cụ thể:

• Giả sử ta có góc nhiễu xạ \(\theta = 20^\circ\) và bước sóng tia X \(\lambda = 1.54 \, \mathring{A}\).
• Áp dụng phương trình Bragg: \[ d = \frac{1.54 \, \mathring{A}}{2\sin 20^\circ} = 2.24 \, \mathring{A} \]

Như vậy, khoảng cách giữa các mặt phẳng nguyên tử trong tinh thể là \(d = 2.24 \, \mathring{A}\).

Trong bài tập này, chúng ta sẽ thực hiện các bước đánh giá độ ổn định của cấu trúc tinh thể dựa trên dữ liệu nhiễu xạ tia X (XRD). Phương pháp này giúp chúng ta xác định các đặc điểm quan trọng của tinh thể như cấu trúc, kích thước hạt, và khuyết tật tinh thể.

Các bước thực hiện:

1. Chuẩn bị mẫu: Mẫu cần được chuẩn bị kỹ lưỡng, đảm bảo bề mặt phẳng và sạch sẽ để kết quả nhiễu xạ không bị nhiễu.
2. Thu thập dữ liệu nhiễu xạ: Đưa mẫu vào thiết bị XRD để thu thập phổ nhiễu xạ tia X. Đỉnh nhiễu xạ thu được sẽ cung cấp thông tin về cấu trúc tinh thể.
3. Phân tích phổ nhiễu xạ: Sử dụng phần mềm để phân tích các đỉnh nhiễu xạ. Độ cao và vị trí của các đỉnh này giúp xác định kích thước hạt tinh thể và các khuyết tật có thể có.
4. So sánh với mẫu tham chiếu: So sánh phổ nhiễu xạ của mẫu với dữ liệu chuẩn (ví dụ: cơ sở dữ liệu ICDD) để xác định tính ổn định của cấu trúc tinh thể.

Công thức cần sử dụng:

Để tính toán khoảng cách giữa các mặt phẳng tinh thể, ta sử dụng Định luật Bragg:

Trong đó:

• n: Số nguyên, chỉ bậc nhiễu xạ
• \(\lambda\): Bước sóng tia X
• d: Khoảng cách giữa các mặt tinh thể
• \(\theta\): Góc nhiễu xạ

Đánh giá độ ổn định:

Để đánh giá độ ổn định của cấu trúc tinh thể, cần xem xét các yếu tố sau:

• Kích thước hạt tinh thể: Kích thước hạt càng nhỏ, cấu trúc càng ổn định.
• Sự hiện diện của khuyết tật: Số lượng và loại khuyết tật tinh thể có thể ảnh hưởng đến độ bền của cấu trúc.
• So sánh với mẫu chuẩn: Nếu phổ nhiễu xạ khớp với mẫu chuẩn, điều này cho thấy cấu trúc tinh thể ổn định.

Kết quả phân tích nhiễu xạ giúp xác định chính xác độ ổn định cấu trúc của mẫu, từ đó đưa ra các đánh giá chính xác về tính chất vật liệu.

Kích thước hạt của một vật liệu có thể ảnh hưởng trực tiếp đến cường độ và vị trí các đỉnh nhiễu xạ trong phổ nhiễu xạ X-ray (XRD). Khi kích thước hạt giảm, các đỉnh nhiễu xạ có xu hướng mở rộng và giảm cường độ, điều này có thể được sử dụng để đánh giá các đặc điểm cấu trúc của mẫu vật liệu.

Trong bài tập này, chúng ta sẽ sử dụng phương trình Scherrer để tính kích thước hạt từ các dữ liệu nhiễu xạ X-ray:

Trong đó:

• \(D\): Kích thước hạt (nm)
• \(K\): Hằng số Scherrer, thường có giá trị từ 0.9 đến 1
• \(\lambda\): Bước sóng của tia X (thường là 0.154 nm cho Cu-K\alpha)
• \(\beta\): Độ rộng toàn phần của đỉnh nhiễu xạ tại nửa cường độ cực đại (FWHM), tính bằng radian
• \(\theta\): Góc nhiễu xạ

Bước 1: Thu thập dữ liệu nhiễu xạ X-ray của mẫu vật liệu. Dữ liệu này bao gồm các thông số góc nhiễu xạ (\(2\theta\)) và cường độ.

Bước 2: Xác định đỉnh nhiễu xạ quan trọng và đo độ rộng toàn phần tại nửa cường độ cực đại (\(\beta\)) của đỉnh đó.

Bước 3: Áp dụng phương trình Scherrer để tính toán kích thước hạt dựa trên giá trị \(\beta\), \(\theta\), và \(\lambda\).

Bước 4: Phân tích sự thay đổi kích thước hạt dựa trên các đỉnh nhiễu xạ. Nếu kích thước hạt giảm, chúng ta sẽ thấy sự mở rộng của các đỉnh nhiễu xạ và sự suy giảm cường độ.

Kết quả từ các bước này có thể giúp đánh giá ảnh hưởng của kích thước hạt đến cấu trúc và tính chất của vật liệu, cũng như so sánh với các nghiên cứu trước đó để đưa ra những kết luận về tính ổn định của cấu trúc tinh thể.

Trong bài tập này, chúng ta sẽ sử dụng phương pháp Nhiễu xạ tia X (XRD) để xác định độ tinh khiết của mẫu vật liệu. Kỹ thuật XRD cho phép chúng ta phân tích và đánh giá các đặc tính cấu trúc của mẫu thông qua việc đo đạc và phân tích các đỉnh nhiễu xạ từ mẫu tinh thể.

Các bước để tiến hành bài tập:

1. Chuẩn bị mẫu vật liệu và tiến hành đo đạc nhiễu xạ tia X.
2. Thu thập dữ liệu từ thiết bị XRD và vẽ đồ thị phân bố các đỉnh nhiễu xạ.
3. Phân tích các đỉnh nhiễu xạ để xác định các thành phần cấu trúc của mẫu. Đối với một mẫu tinh khiết, các đỉnh nhiễu xạ sẽ sắc nét và tuân theo một mẫu phân bố đều.
4. So sánh với cơ sở dữ liệu ICDD để kiểm tra sự phù hợp giữa mẫu đo và mẫu tham chiếu.
5. Tính toán độ tinh khiết dựa trên tỉ lệ các pha tinh thể tìm được trong mẫu.

Biểu thức toán học để tính độ tinh khiết của mẫu có thể được biểu diễn bằng:

Một ví dụ cụ thể:

• Mẫu XRD của bạn có 2 đỉnh chính thuộc về pha tinh thể A.
• Mẫu cũng có 1 đỉnh nhỏ thuộc về pha tinh thể B.
• Tổng số pha tìm được là 3.
• Vậy độ tinh khiết của pha A là:

Đây là một phương pháp hiệu quả để xác định độ tinh khiết của mẫu vật liệu và đóng vai trò quan trọng trong việc đánh giá chất lượng của sản phẩm.

Kỹ thuật nhiễu xạ tia X (XRD) là công cụ mạnh mẽ trong việc phân tích sự biến dạng của tinh thể. Bằng cách theo dõi các đỉnh nhiễu xạ và sự thay đổi của chúng, ta có thể rút ra kết luận về độ biến dạng trong mạng tinh thể. Bài tập này sẽ giúp bạn hiểu rõ quá trình phân tích sự biến dạng tinh thể thông qua dữ liệu XRD.

Bước 1: Thu thập phổ nhiễu xạ XRD

Để bắt đầu, chúng ta cần thu thập phổ nhiễu xạ XRD của mẫu tinh thể. Dữ liệu phổ này chứa thông tin về các đỉnh nhiễu xạ, đặc trưng cho cấu trúc tinh thể của mẫu.

Bước 2: Phân tích sự thay đổi vị trí đỉnh nhiễu xạ

Các đỉnh nhiễu xạ xuất hiện tại các vị trí góc \( \theta \) cụ thể. Sự biến dạng trong mạng tinh thể có thể làm dịch chuyển các đỉnh này. Công thức Bragg giúp xác định mối liên hệ giữa vị trí đỉnh và cấu trúc tinh thể:

Trong đó:

• \( d \): khoảng cách giữa các mặt phẳng nguyên tử
• \( \theta \): góc nhiễu xạ
• \( \lambda \): bước sóng tia X
• \( n \): bậc nhiễu xạ (thường là 1)

Bước 3: Đo độ biến dạng

Sự biến dạng của mạng tinh thể được xác định dựa trên sự thay đổi khoảng cách giữa các mặt phẳng nguyên tử \( d \). Công thức biến dạng tinh thể được tính như sau:

Ở đây, \( \varepsilon \) là độ biến dạng, \( d_{biến dạng} \) là khoảng cách giữa các mặt phẳng khi bị biến dạng, và \( d_{ban đầu} \) là khoảng cách ban đầu của mạng tinh thể.

Bước 4: Xác định mức độ khuyết tật tinh thể

Sự biến dạng của tinh thể thường đi kèm với các khuyết tật, như sự dịch chuyển vị trí nguyên tử. Khuyết tật này có thể ảnh hưởng đến cường độ và hình dạng của đỉnh nhiễu xạ. Việc so sánh kết quả XRD với dữ liệu tham chiếu từ cơ sở dữ liệu nhiễu xạ (như ICDD) sẽ giúp xác định mức độ khuyết tật.

Bước 5: Đánh giá và kết luận

Sau khi phân tích các dữ liệu XRD, bạn sẽ có thể rút ra kết luận về mức độ biến dạng và khuyết tật của tinh thể. Kết quả này rất quan trọng trong việc hiểu rõ hơn về tính chất của vật liệu.

Trong bài tập này, chúng ta sẽ tính toán các thông số mạng tinh thể dựa trên dữ liệu nhiễu xạ tia X (XRD). Phân tích kết quả XRD giúp xác định khoảng cách giữa các mặt phẳng nguyên tử và từ đó tính toán các thông số mạng như hằng số mạng \( a \), \( b \), và \( c \).

Bước 1: Thu thập phổ nhiễu xạ XRD

Trước tiên, ta cần thu thập phổ XRD của mẫu tinh thể. Các đỉnh nhiễu xạ trong phổ này thể hiện sự phản xạ của tia X từ các mặt phẳng nguyên tử trong mạng tinh thể.

Bước 2: Xác định khoảng cách giữa các mặt phẳng nguyên tử

Sử dụng phương trình Bragg, ta có thể tính toán khoảng cách giữa các mặt phẳng nguyên tử \( d \) theo công thức:

Trong đó:

• \( d \): khoảng cách giữa các mặt phẳng nguyên tử
• \( \theta \): góc nhiễu xạ
• \( \lambda \): bước sóng tia X (thường là 1.54 Å)
• \( n \): bậc nhiễu xạ (thường là 1)

Bước 3: Tính toán hằng số mạng

Với các mạng tinh thể đơn giản như lập phương hay lục giác, các hằng số mạng \( a \), \( b \), và \( c \) có thể được tính từ khoảng cách \( d \) và các chỉ số mặt phẳng Miller (h, k, l). Công thức tính toán cho mạng lập phương là:

Ở đây:

• \( h, k, l \): các chỉ số Miller của mặt phẳng tinh thể
• \( a \): hằng số mạng

Bước 4: Xác định cấu trúc tinh thể

Sau khi tính toán hằng số mạng, ta có thể so sánh kết quả với các thông số cấu trúc đã biết từ các tài liệu tham khảo (thường được lưu trữ trong các cơ sở dữ liệu như ICDD). Điều này giúp xác định cấu trúc tinh thể của mẫu một cách chính xác.

Bước 5: Đánh giá kết quả

Sau khi hoàn thành các bước trên, bạn có thể rút ra kết luận về các thông số mạng của tinh thể, từ đó hiểu rõ hơn về tính chất cấu trúc của vật liệu đang nghiên cứu.