Nhiễu Xạ Fraunhofer: Khám Phá Hiện Tượng Quang Học Đặc Biệt Trong Vật Lý

Nhiễu xạ Fraunhofer là một hiện tượng quan trọng trong quang học, giúp phân tích quang phổ ánh sáng thông qua cách tử nhiễu xạ. Hiện tượng này được ứng dụng rộng rãi trong nhiều lĩnh vực như vật lý, thiên văn học, và nghiên cứu vật liệu.

Nguyên Lý Hoạt Động

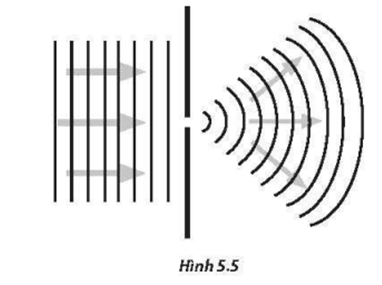
Nhiễu xạ Fraunhofer xảy ra khi một chùm ánh sáng song song chiếu qua một cách tử hoặc khe hẹp, tạo ra các vân nhiễu xạ trên màn hoặc cảm biến. Điều kiện để có sự nhiễu xạ là góc lệch α giữa các tia ló phải thỏa mãn phương trình:

\[
d\sin\alpha = k\lambda
\]

Trong đó:

• d: khoảng cách giữa các khe của cách tử
• λ: bước sóng của ánh sáng
• k: một số nguyên (bậc của vân nhiễu xạ)

Ứng Dụng Thực Tiễn

Hiện tượng nhiễu xạ Fraunhofer được sử dụng để phân tích quang phổ của ánh sáng, giúp xác định các đặc tính quang học của vật liệu và các chất khí. Nó cũng đóng vai trò quan trọng trong việc nghiên cứu cấu trúc tinh thể, đo đạc chính xác khoảng cách giữa các nguyên tử trong tinh thể.

Thí Nghiệm Điển Hình

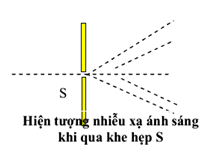
Trong thí nghiệm, một khe hẹp được đặt trước nguồn sáng để tạo ra chùm sáng song song, sau đó chiếu qua cách tử. Các vân sáng tối xuất hiện trên màn quan sát, thể hiện sự nhiễu xạ của ánh sáng tại các góc khác nhau:

\[
\sin\alpha = \frac{x}{\sqrt{x^2 + L^2}}
\]

Trong đó:

• x: khoảng cách từ vị trí vân sáng đến trung tâm
• L: khoảng cách từ khe sáng đến cách tử

Kết Luận

Nhiễu xạ Fraunhofer là một phương pháp mạnh mẽ để nghiên cứu các tính chất quang học của vật liệu. Nhờ vào khả năng phân tích chính xác các thành phần quang phổ, hiện tượng này được sử dụng rộng rãi trong nhiều ngành khoa học và kỹ thuật.

Nhiễu xạ Fraunhofer là một hiện tượng quan trọng trong quang học, xuất hiện khi sóng ánh sáng tương tác với các vật thể nhỏ, tạo ra các mô hình nhiễu xạ. Hiện tượng này được mô tả bằng cách sử dụng các nguyên lý của cơ học sóng và được áp dụng rộng rãi trong các lĩnh vực như phân tích quang phổ, chế tạo cách tử, và nghiên cứu vật liệu.

Trong nhiễu xạ Fraunhofer, ánh sáng từ một nguồn điểm hoặc một khe hẹp truyền qua các vật thể nhỏ hoặc lỗ hẹp và tạo ra một mô hình nhiễu xạ trên màn quan sát. Mô hình này bao gồm các vân sáng và tối xen kẽ, có thể được phân tích để tìm hiểu về các đặc tính của nguồn sáng hoặc vật thể tạo ra nhiễu xạ.

Để hiểu rõ hơn, ta xem xét mô hình nhiễu xạ từ một khe hẹp:

• Ánh sáng đơn sắc có bước sóng \(\lambda\) chiếu qua một khe có chiều rộng \(a\).
• Góc nhiễu xạ \(\theta\) được xác định bằng phương trình: \(\sin(\theta) = \frac{m\lambda}{a}\), với \(m\) là số thứ tự của cực đại.
• Các vân sáng xuất hiện tại các vị trí mà sóng ánh sáng từ các điểm khác nhau trên khe giao thoa với nhau theo pha.

Trong thực tế, nhiễu xạ Fraunhofer còn được ứng dụng trong việc thiết kế và phân tích các hệ thống quang học như máy ảnh, kính hiển vi, và các thiết bị đo đạc chính xác.

Bằng cách áp dụng nhiễu xạ Fraunhofer, các nhà khoa học có thể đo lường được các thông số quan trọng của vật liệu, từ đó đóng góp vào sự phát triển của công nghệ và khoa học hiện đại.

Để hiểu rõ hơn về hiện tượng nhiễu xạ Fraunhofer, chúng ta sẽ đi qua một số bài tập áp dụng các nguyên lý quang học liên quan. Các bài tập này sẽ giúp bạn nắm vững cách tính toán và phân tích các kết quả nhiễu xạ, từ đó hiểu rõ hơn về ứng dụng của hiện tượng này trong thực tiễn.

1. Bài tập 1: Tính góc nhiễu xạ lớn nhất

   Cho một khe hẹp có chiều rộng \(a = 0.5 \, \text{mm}\) và ánh sáng đơn sắc có bước sóng \(\lambda = 600 \, \text{nm}\). Tính góc nhiễu xạ lớn nhất \(\theta\) mà tại đó vân sáng xuất hiện.

   Lời giải:

   • Áp dụng công thức nhiễu xạ: \(\sin(\theta) = \frac{m\lambda}{a}\), với \(m = 1\).
   • Tính toán: \(\sin(\theta) = \frac{1 \times 600 \times 10^{-9}}{0.5 \times 10^{-3}} = 1.2 \times 10^{-3}\).
   • Suy ra: \(\theta \approx 0.0688^\circ\).

2. Bài tập 2: Xác định khoảng cách giữa các vân sáng

   Một khe hẹp có chiều rộng \(a = 0.3 \, \text{mm}\), ánh sáng có bước sóng \(\lambda = 500 \, \text{nm}\), khoảng cách từ khe đến màn quan sát \(D = 2 \, \text{m}\). Tính khoảng cách giữa các vân sáng liên tiếp trên màn.

   Lời giải:

   • Khoảng cách giữa các vân sáng được tính bằng công thức: \(\Delta y = \frac{\lambda D}{a}\).
   • Tính toán: \(\Delta y = \frac{500 \times 10^{-9} \times 2}{0.3 \times 10^{-3}} = 3.33 \, \text{mm}\).

3. Bài tập 3: Tính số vân sáng

   Cho ánh sáng có bước sóng \(\lambda = 700 \, \text{nm}\) chiếu qua một khe có chiều rộng \(a = 0.7 \, \text{mm}\). Tính số vân sáng quan sát được trên màn cách khe \(D = 3 \, \text{m}\).

   Lời giải:

   • Số vân sáng được tính bằng công thức: \(m_{\text{max}} = \left\lfloor \frac{a}{\lambda} \right\rfloor\).
   • Tính toán: \(m_{\text{max}} = \left\lfloor \frac{0.7 \times 10^{-3}}{700 \times 10^{-9}} \right\rfloor = 1\).
   • Suy ra chỉ có một vân sáng chính giữa và hai vân tối ở hai bên.