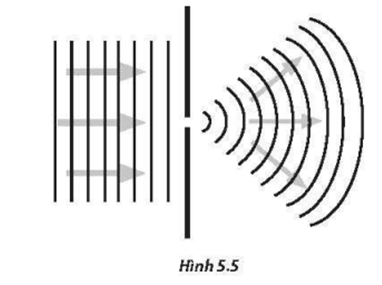
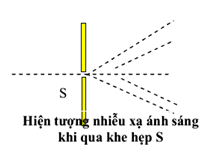
Chủ đề nhiễu xạ qua lỗ tròn: Nhiễu xạ qua lỗ tròn là hiện tượng quan trọng trong quang học, với nhiều ứng dụng thực tiễn từ khoa học cơ bản đến công nghệ hiện đại. Bài viết này sẽ khám phá chi tiết cơ chế nhiễu xạ, công thức tính toán, và những ứng dụng nổi bật của hiện tượng này, giúp bạn nắm vững kiến thức và hiểu rõ hơn về nhiễu xạ ánh sáng.
Nhiễu Xạ Qua Lỗ Tròn
Trong lĩnh vực quang học, nhiễu xạ qua lỗ tròn là một hiện tượng quan trọng. Hiện tượng này xảy ra khi một chùm ánh sáng đi qua một lỗ tròn có kích thước nhỏ hơn bước sóng của ánh sáng đó, làm cho ánh sáng bị bẻ cong và tạo ra các vòng sáng tối trên màn chiếu.
1. Nguyên lý cơ bản
Khi ánh sáng đi qua một lỗ tròn, các sóng ánh sáng bị tán xạ theo mọi hướng từ rìa của lỗ. Hiện tượng này có thể được mô tả bằng nguyên lý Huygens-Fresnel, trong đó mỗi điểm trên mặt sóng được coi như một nguồn phát sóng thứ cấp lan tỏa.
2. Công thức tính toán
Công thức tính cường độ ánh sáng tại một điểm trên màn chiếu cách lỗ tròn một khoảng cách nhất định có thể được biểu diễn bằng phương trình:
\[
I(\theta) = I_0 \left( \frac{2J_1(k \cdot a \cdot \sin(\theta))}{k \cdot a \cdot \sin(\theta)} \right)^2
\]
Trong đó:
- \(I(\theta)\): Cường độ ánh sáng tại góc \(\theta\).
- \(I_0\): Cường độ ánh sáng tại trung tâm.
- \(J_1\): Hàm Bessel bậc nhất.
- \(k\): Số sóng, \(\frac{2\pi}{\lambda}\).
- \(a\): Bán kính của lỗ tròn.
- \(\theta\): Góc so với trục quang học.
3. Ứng dụng trong thực tế
Hiện tượng nhiễu xạ qua lỗ tròn có nhiều ứng dụng quan trọng trong quang học và kỹ thuật, bao gồm:
- Thiết kế các thiết bị quang học như kính hiển vi, máy ảnh, và các hệ thống quang học khác.
- Nghiên cứu cấu trúc của các vật liệu ở cấp độ vi mô bằng cách sử dụng ánh sáng để tạo ra các mẫu nhiễu xạ.
- Xác định kích thước của các hạt nhỏ trong môi trường thông qua phân tích mẫu nhiễu xạ.
4. Bài toán mẫu
Giả sử có một lỗ tròn với bán kính \(a = 0.5\) mm. Ánh sáng có bước sóng \(\lambda = 600\) nm chiếu qua lỗ này. Tính cường độ sáng tại điểm cách lỗ một khoảng 1 m trên màn chiếu ở góc \(\theta = 5^\circ\).
Sử dụng công thức:
\[
k = \frac{2\pi}{\lambda} = \frac{2\pi}{600 \times 10^{-9}} = 1.047 \times 10^7 \text{ rad/m}
\]
Thay các giá trị vào công thức, ta có thể tính được giá trị của cường độ sáng \(I(\theta)\).
5. Kết luận
Nhiễu xạ qua lỗ tròn là một hiện tượng cơ bản nhưng cực kỳ quan trọng trong quang học. Hiểu rõ về hiện tượng này không chỉ giúp nâng cao kiến thức lý thuyết mà còn có ứng dụng rộng rãi trong thực tế, từ nghiên cứu khoa học đến thiết kế các thiết bị quang học hiện đại.

.png)
Mục Lục
1. Giới thiệu về nhiễu xạ ánh sáng
2. Hiện tượng nhiễu xạ qua lỗ tròn
3. Công thức và cách tính nhiễu xạ qua lỗ tròn
4. Ứng dụng của nhiễu xạ qua lỗ tròn trong thực tiễn
5. Các thí nghiệm nhiễu xạ điển hình
6. Mô hình Fresnel và nhiễu xạ qua lỗ tròn
7. So sánh nhiễu xạ qua lỗ tròn với các dạng nhiễu xạ khác
8. Những yếu tố ảnh hưởng đến hiện tượng nhiễu xạ
9. Bài tập ví dụ và lời giải chi tiết về nhiễu xạ qua lỗ tròn
10. Tài liệu tham khảo và đề thi mẫu
Bài Tập Thực Hành Nhiễu Xạ Qua Lỗ Tròn
Bài Tập 1: Tính toán khoảng cách giữa các vân nhiễu xạ
Cho một chùm ánh sáng đơn sắc có bước sóng \(\lambda = 600 \, nm\) chiếu vuông góc qua một lỗ tròn có bán kính \(R = 0.1 \, mm\). Tính khoảng cách giữa hai vân nhiễu xạ bậc nhất trên màn cách lỗ tròn \(D = 2 \, m\).
Gợi ý: Sử dụng công thức tính góc nhiễu xạ \(\theta\) và công thức tính khoảng cách giữa các vân nhiễu xạ.
Bài Tập 2: Xác định bán kính lỗ tròn từ hiện tượng nhiễu xạ
Trong một thí nghiệm, người ta chiếu ánh sáng có bước sóng \(\lambda = 500 \, nm\) qua một lỗ tròn và quan sát thấy các vân sáng trên màn cách lỗ tròn một khoảng \(D = 1.5 \, m\). Bán kính lỗ tròn được xác định qua khoảng cách giữa hai vân nhiễu xạ bậc nhất là \(2.5 \, mm\). Hãy tính bán kính của lỗ tròn.
Gợi ý: Áp dụng công thức cho khoảng cách giữa các vân nhiễu xạ và giải phương trình tìm \(R\).
Bài Tập 3: Tính độ rộng vân sáng trung tâm
Một chùm ánh sáng có bước sóng \(\lambda = 450 \, nm\) chiếu qua một lỗ tròn có bán kính \(R = 0.05 \, mm\). Màn quan sát đặt cách lỗ tròn một khoảng \(D = 1 \, m\). Tính độ rộng của vân sáng trung tâm trên màn.
Gợi ý: Độ rộng vân sáng trung tâm phụ thuộc vào bán kính lỗ tròn và khoảng cách đến màn quan sát.
Bài Tập 4: Phân tích ảnh hưởng của bước sóng đến nhiễu xạ
So sánh khoảng cách giữa các vân nhiễu xạ khi chiếu ánh sáng có bước sóng \(\lambda_1 = 500 \, nm\) và \(\lambda_2 = 700 \, nm\) qua cùng một lỗ tròn có bán kính \(R = 0.1 \, mm\). Màn quan sát cách lỗ tròn \(D = 2 \, m\). Nhận xét sự khác biệt.
Gợi ý: Đưa ra kết luận về mối quan hệ giữa bước sóng và khoảng cách giữa các vân nhiễu xạ.
Bài Tập 5: Tính số vân sáng trong một vùng quan sát
Cho chùm ánh sáng có bước sóng \(\lambda = 600 \, nm\) chiếu qua một lỗ tròn có bán kính \(R = 0.08 \, mm\). Vùng quan sát trên màn có đường kính \(D = 0.02 \, m\). Tính số vân sáng xuất hiện trong vùng quan sát này.
Gợi ý: Sử dụng công thức tính số vân sáng và áp dụng vào vùng quan sát cụ thể.
Bài Tập 6: Phân tích sự thay đổi vị trí các vân khi thay đổi khoảng cách đến màn
Trong một thí nghiệm, người ta chiếu ánh sáng có bước sóng \(\lambda = 550 \, nm\) qua một lỗ tròn và đo khoảng cách giữa hai vân sáng bậc nhất trên màn ở các khoảng cách khác nhau từ \(D_1 = 1 \, m\) đến \(D_2 = 2 \, m\). Hãy phân tích và vẽ đồ thị biểu diễn sự thay đổi vị trí các vân sáng.
Gợi ý: Lập phương trình mô tả sự thay đổi vị trí vân sáng theo khoảng cách đến màn và vẽ đồ thị tương ứng.
Bài Tập 7: Tính nhiễu xạ qua lỗ tròn trong môi trường có chiết suất khác nhau
Xét chùm ánh sáng đơn sắc có bước sóng \(\lambda = 650 \, nm\) chiếu qua lỗ tròn có bán kính \(R = 0.1 \, mm\). Màn quan sát đặt cách lỗ tròn một khoảng \(D = 1.5 \, m\) trong không khí và sau đó trong môi trường có chiết suất \(n = 1.33\). Hãy so sánh khoảng cách giữa các vân nhiễu xạ trong hai trường hợp này.
Gợi ý: Áp dụng công thức cho nhiễu xạ và điều chỉnh bước sóng theo chiết suất môi trường.
Bài Tập 8: Tính số vân tối trong một khoảng cách xác định
Một chùm ánh sáng đơn sắc có bước sóng \(\lambda = 700 \, nm\) chiếu qua một lỗ tròn có bán kính \(R = 0.12 \, mm\). Tính số vân tối xuất hiện trong khoảng cách từ \(D_1 = 0.5 \, m\) đến \(D_2 = 1.5 \, m\) trên màn.
Gợi ý: Áp dụng công thức tính số vân tối trong khoảng cách được xác định và đưa ra kết luận.
Bài Tập 9: Phân tích ảnh hưởng của kích thước lỗ tròn đến độ rõ nét của các vân nhiễu xạ
Thí nghiệm cho ánh sáng có bước sóng \(\lambda = 600 \, nm\) chiếu qua hai lỗ tròn có bán kính khác nhau \(R_1 = 0.1 \, mm\) và \(R_2 = 0.05 \, mm\). Màn quan sát đặt cách lỗ tròn \(D = 1.5 \, m\). Hãy phân tích và so sánh độ rõ nét của các vân nhiễu xạ.
Gợi ý: Xem xét ảnh hưởng của bán kính lỗ tròn đến độ rõ nét của các vân và đưa ra kết luận.
Bài Tập 10: Tính góc nhiễu xạ cực đại
Một chùm ánh sáng có bước sóng \(\lambda = 500 \, nm\) chiếu qua một lỗ tròn có bán kính \(R = 0.08 \, mm\). Tính góc nhiễu xạ tại cực đại thứ hai trên màn cách lỗ tròn \(D = 1 \, m\).
Gợi ý: Sử dụng công thức tính góc nhiễu xạ và áp dụng vào trường hợp cụ thể.