Chủ đề bài tập nhiễu xạ tia x: Bài viết này cung cấp một cái nhìn tổng quan về nhiễu xạ tia X, từ nguyên lý cơ bản đến các dạng bài tập ứng dụng thực tiễn. Bạn sẽ khám phá cách phân tích kết quả và sử dụng phương pháp này trong nghiên cứu khoa học cũng như công nghiệp, giúp nâng cao hiểu biết và kỹ năng của bạn trong lĩnh vực này.
Mục lục
- Bài Tập Nhiễu Xạ Tia X
- Mục Lục Tổng Hợp
- 10 Dạng Bài Tập Có Lời Giải Hoàn Chỉnh
- Bài Tập 1: Tính Góc Nhiễu Xạ Từ Khoảng Cách Mặt Phẳng
- Bài Tập 2: Xác Định Bậc Nhiễu Xạ Của Một Tinh Thể
- Bài Tập 3: Tính Khoảng Cách Mặt Phẳng Khi Biết Góc Nhiễu Xạ
- Bài Tập 4: Phân Tích Cấu Trúc Tinh Thể Từ Kết Quả Nhiễu Xạ
- Bài Tập 5: So Sánh Kết Quả Nhiễu Xạ Giữa Hai Mẫu Vật Khác Nhau
- Bài Tập 6: Ứng Dụng Phương Trình Bragg Trong Tính Toán Khoảng Cách
- Bài Tập 7: Xác Định Thông Số Cấu Trúc Từ Dữ Liệu Nhiễu Xạ
- Bài Tập 8: Phân Tích Kết Quả Nhiễu Xạ Của Một Hợp Chất Phức Tạp
- Bài Tập 9: Tính Góc Nhiễu Xạ Cho Các Bước Sóng Khác Nhau
- Bài Tập 10: Ứng Dụng Nhiễu Xạ Tia X Trong Xác Định Thành Phần Hóa Học
Bài Tập Nhiễu Xạ Tia X
Nhiễu xạ tia X là một phương pháp quan trọng trong vật lý học và hóa học, được sử dụng rộng rãi để nghiên cứu cấu trúc của vật liệu. Các bài tập liên quan đến nhiễu xạ tia X thường xoay quanh việc tính toán các tham số như khoảng cách mặt phẳng, góc nhiễu xạ, và các thông số cấu trúc khác của tinh thể.
1. Nguyên Lý Cơ Bản
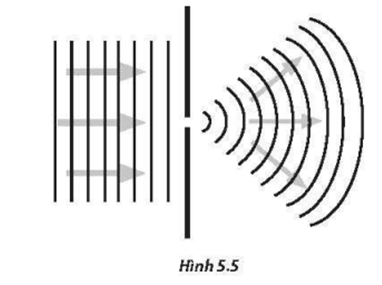
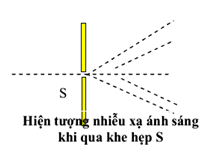
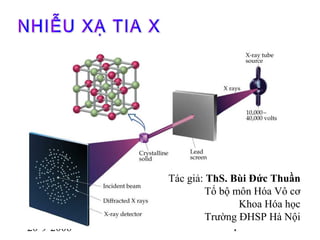
Nhiễu xạ tia X dựa trên nguyên lý Bragg, trong đó tia X bị nhiễu xạ bởi các mặt phẳng nguyên tử trong tinh thể. Điều kiện nhiễu xạ Bragg được biểu diễn bởi phương trình:
\[n\lambda = 2d\sin\theta\]
Trong đó:
- \(n\) là số bậc của nhiễu xạ (thường là 1).
- \(\lambda\) là bước sóng của tia X.
- \(d\) là khoảng cách giữa các mặt phẳng nguyên tử trong tinh thể.
- \(\theta\) là góc nhiễu xạ.
2. Bài Tập Mẫu
Giả sử bạn có một tinh thể với khoảng cách mặt phẳng \(d = 2.5\) Å và tia X có bước sóng \(\lambda = 1.54\) Å. Hãy tính góc nhiễu xạ \(\theta\) cho bậc nhiễu xạ thứ nhất.
Lời giải:
Theo phương trình Bragg:
\[n\lambda = 2d\sin\theta\]
Với \(n = 1\), ta có:
\[1.54 = 2 \times 2.5 \times \sin\theta\]
Từ đó, ta tìm được:
\[\sin\theta = \frac{1.54}{5} = 0.308\]
\[\theta = \arcsin(0.308) \approx 17.98^\circ\]
3. Ứng Dụng Của Nhiễu Xạ Tia X
Nhiễu xạ tia X không chỉ được dùng trong nghiên cứu cấu trúc tinh thể, mà còn có ứng dụng trong nhiều lĩnh vực khác như:
- Phân tích khoáng vật và xác định thành phần vật liệu.
- Nghiên cứu cấu trúc protein và các phân tử sinh học.
- Đánh giá chất lượng vật liệu và kiểm tra khuyết tật trong các sản phẩm công nghiệp.
4. Thực Hành Bài Tập
Các bài tập nhiễu xạ tia X giúp củng cố kiến thức lý thuyết và phát triển kỹ năng giải quyết vấn đề trong thực tế. Dưới đây là một số bài tập mẫu:
- Tính khoảng cách mặt phẳng \(d\) khi biết góc nhiễu xạ \(\theta = 22^\circ\) và bước sóng tia X \(\lambda = 1.54\) Å.
- Giả sử một tinh thể có cấu trúc lập phương tâm mặt với cạnh ô mạng là 4 Å. Tính góc nhiễu xạ cho mặt phẳng (110).
- Xác định bậc nhiễu xạ \(n\) khi biết góc nhiễu xạ \(\theta = 30^\circ\), bước sóng tia X \(\lambda = 1.54\) Å, và khoảng cách mặt phẳng \(d = 3\) Å.
5. Kết Luận
Bài tập nhiễu xạ tia X là một phần quan trọng trong giáo dục và nghiên cứu khoa học, giúp sinh viên và nhà nghiên cứu hiểu rõ hơn về cấu trúc của vật liệu. Qua việc thực hành các bài tập này, người học có thể nắm vững nguyên lý và kỹ thuật phân tích, góp phần vào việc phát triển khoa học và công nghệ.

.png)
Mục Lục Tổng Hợp
Giới Thiệu Về Nhiễu Xạ Tia X
Khái niệm cơ bản về nhiễu xạ tia X, lịch sử phát triển, và ứng dụng trong phân tích vật liệu.
Nguyên Lý Cơ Bản Của Nhiễu Xạ Tia X
Cách nhiễu xạ tia X hoạt động, với các công thức toán học và phương trình Bragg: \[n\lambda = 2d\sin(\theta)\]
Phương Trình Bragg Và Ứng Dụng
Chi tiết về phương trình Bragg, cách áp dụng trong việc xác định cấu trúc tinh thể và các bài toán liên quan.
Phân Tích Cấu Trúc Tinh Thể Bằng Nhiễu Xạ Tia X
Các bước phân tích cấu trúc tinh thể, từ thu thập dữ liệu đến giải mã thông tin cấu trúc.
Các Loại Mẫu Vật Dùng Trong Nhiễu Xạ Tia X
Phân loại và đặc điểm của các mẫu vật khác nhau, từ tinh thể đơn đến hợp chất phức tạp.
Phương Pháp Chuẩn Bị Mẫu Vật
Hướng dẫn chuẩn bị mẫu vật cho phân tích nhiễu xạ tia X, bao gồm các kỹ thuật cắt, mài và bảo quản.
Ứng Dụng Của Nhiễu Xạ Tia X Trong Công Nghiệp
Các ứng dụng thực tiễn của nhiễu xạ tia X trong công nghiệp, như kiểm tra chất lượng vật liệu và nghiên cứu phát triển sản phẩm.
Phân Tích Dữ Liệu Nhiễu Xạ Tia X
Cách thu thập và phân tích dữ liệu nhiễu xạ, bao gồm các phần mềm và công cụ hỗ trợ.
So Sánh Nhiễu Xạ Tia X Với Các Phương Pháp Khác
Đánh giá ưu, nhược điểm của nhiễu xạ tia X so với các phương pháp phân tích cấu trúc khác như NMR hay SEM.
Những Thách Thức Và Giải Pháp Trong Nghiên Cứu Nhiễu Xạ Tia X
Những khó khăn thường gặp khi nghiên cứu nhiễu xạ tia X và các phương pháp khắc phục.
10 Dạng Bài Tập Có Lời Giải Hoàn Chỉnh
-
Bài Tập 1: Xác Định Khoảng Cách Mặt Phẳng Trong Tinh Thể
Cho tia X có bước sóng \(\lambda = 1.54 \, \text{Å}\) chiếu vào mẫu vật với góc nhiễu xạ \(\theta = 30^\circ\). Tìm khoảng cách giữa các mặt phẳng trong tinh thể \((d)\) bằng phương trình Bragg: \[n\lambda = 2d\sin(\theta)\]
Giải: Sử dụng phương trình Bragg và thay số, ta có \(d = \frac{n\lambda}{2\sin(\theta)} = \frac{1.54}{2\sin(30^\circ)} = 1.54 \, \text{Å}\).
-
Bài Tập 2: Tính Góc Nhiễu Xạ
Một mẫu tinh thể có khoảng cách mặt phẳng \(d = 2.28 \, \text{Å}\). Tia X có bước sóng \(\lambda = 1.54 \, \text{Å}\). Tìm góc nhiễu xạ \(\theta\).
Giải: Sử dụng phương trình Bragg: \(\sin(\theta) = \frac{n\lambda}{2d} = \frac{1.54}{2 \times 2.28} = 0.338\), suy ra \(\theta = \arcsin(0.338) \approx 19.7^\circ\).
-
Bài Tập 3: Tìm Bước Sóng Của Tia X
Tìm bước sóng \(\lambda\) của tia X khi góc nhiễu xạ \(\theta = 45^\circ\) và khoảng cách mặt phẳng trong tinh thể \(d = 3.2 \, \text{Å}\).
Giải: Sử dụng phương trình Bragg: \(\lambda = 2d\sin(\theta) = 2 \times 3.2 \times \sin(45^\circ) = 4.52 \, \text{Å}\).
-
Bài Tập 4: Tính Số Bậc Của Phản Xạ
Cho tia X có bước sóng \(\lambda = 1.94 \, \text{Å}\), góc nhiễu xạ \(\theta = 25^\circ\), và khoảng cách mặt phẳng \(d = 3.9 \, \text{Å}\). Tính số bậc \(n\) của phản xạ.
Giải: Sử dụng phương trình Bragg: \(n = \frac{2d\sin(\theta)}{\lambda} = \frac{2 \times 3.9 \times \sin(25^\circ)}{1.94} \approx 1\).
-
Bài Tập 5: Phân Tích Cấu Trúc Tinh Thể
Mô tả quy trình phân tích cấu trúc tinh thể sử dụng dữ liệu nhiễu xạ tia X từ thực nghiệm, bao gồm việc xác định không gian mạng và vị trí nguyên tử trong mạng.
-
Bài Tập 6: Xác Định Cấu Trúc Tinh Thể Từ Dữ Liệu Nhiễu Xạ
Cho dữ liệu nhiễu xạ của một tinh thể, xác định cấu trúc tinh thể bằng cách phân tích các đỉnh nhiễu xạ và ứng dụng phương trình Bragg.
-
Bài Tập 7: Tính Chỉ Số Miller Từ Dữ Liệu Nhiễu Xạ
Phân tích một mẫu tinh thể và xác định các chỉ số Miller \((hkl)\) từ dữ liệu nhiễu xạ thu được.
-
Bài Tập 8: Tính Độ Dài Liên Kết Trong Tinh Thể
Sử dụng dữ liệu nhiễu xạ tia X để tính toán độ dài liên kết trong một mạng tinh thể cụ thể.
-
Bài Tập 9: Xác Định Vị Trí Nguyên Tử Trong Mạng
Dựa trên các kết quả nhiễu xạ, xác định vị trí của nguyên tử trong mạng tinh thể.
-
Bài Tập 10: So Sánh Kết Quả Nhiễu Xạ Với Mô Hình Lý Thuyết
So sánh kết quả nhiễu xạ tia X thực nghiệm với mô hình lý thuyết và đánh giá sự phù hợp.

Bài Tập 1: Tính Góc Nhiễu Xạ Từ Khoảng Cách Mặt Phẳng
Trong bài tập này, chúng ta sẽ tính góc nhiễu xạ \(\theta\) từ khoảng cách mặt phẳng \((d)\) trong tinh thể khi biết bước sóng của tia X \(\lambda\). Công thức Bragg được sử dụng để liên hệ giữa các đại lượng này:
\[ n\lambda = 2d\sin(\theta) \]
Bước 1: Xác định các thông số đã cho:
- Bước sóng tia X \(\lambda = 1.54 \, \text{Å}\)
- Khoảng cách mặt phẳng \(d = 2.28 \, \text{Å}\)
- Thứ tự nhiễu xạ \(n = 1\) (phản xạ bậc nhất)
Bước 2: Sắp xếp lại phương trình Bragg để tìm góc nhiễu xạ:
\[ \sin(\theta) = \frac{n\lambda}{2d} \]
Bước 3: Thay các giá trị vào công thức:
\[ \sin(\theta) = \frac{1 \times 1.54 \, \text{Å}}{2 \times 2.28 \, \text{Å}} \approx 0.338 \]
Bước 4: Tính toán góc nhiễu xạ \(\theta\):
\[ \theta = \arcsin(0.338) \approx 19.7^\circ \]
Vậy, góc nhiễu xạ là khoảng \(19.7^\circ\).

Bài Tập 2: Xác Định Bậc Nhiễu Xạ Của Một Tinh Thể
Trong bài tập này, chúng ta sẽ xác định bậc nhiễu xạ \(n\) của một tinh thể khi biết góc nhiễu xạ \(\theta\), bước sóng của tia X \(\lambda\), và khoảng cách mặt phẳng \(d\). Công thức Bragg sẽ được áp dụng để giải bài toán này:
\[ n\lambda = 2d\sin(\theta) \]
Bước 1: Xác định các thông số đã cho:
- Góc nhiễu xạ \(\theta = 30^\circ\)
- Bước sóng tia X \(\lambda = 1.54 \, \text{Å}\)
- Khoảng cách mặt phẳng \(d = 2.28 \, \text{Å}\)
Bước 2: Sắp xếp lại phương trình Bragg để tìm bậc nhiễu xạ \(n\):
\[ n = \frac{2d\sin(\theta)}{\lambda} \]
Bước 3: Thay các giá trị vào công thức:
\[ n = \frac{2 \times 2.28 \, \text{Å} \times \sin(30^\circ)}{1.54 \, \text{Å}} \approx 1.48 \]
Bước 4: Làm tròn kết quả \(n\) về số nguyên gần nhất:
Vậy, bậc nhiễu xạ \(n\) là \(1\) (phản xạ bậc nhất).

Bài Tập 3: Tính Khoảng Cách Mặt Phẳng Khi Biết Góc Nhiễu Xạ
Bài tập này yêu cầu tính khoảng cách mặt phẳng \(d\) trong một tinh thể khi biết góc nhiễu xạ \(\theta\) và bước sóng của tia X \(\lambda\). Chúng ta sẽ sử dụng công thức Bragg để giải quyết bài toán này:
\[ n\lambda = 2d\sin(\theta) \]
Bước 1: Xác định các thông số đã cho:
- Góc nhiễu xạ \(\theta = 20^\circ\)
- Bước sóng tia X \(\lambda = 1.54 \, \text{Å}\)
- Bậc nhiễu xạ \(n = 1\)
Bước 2: Sắp xếp lại phương trình Bragg để tìm khoảng cách mặt phẳng \(d\):
\[ d = \frac{n\lambda}{2\sin(\theta)} \]
Bước 3: Thay các giá trị vào công thức:
\[ d = \frac{1 \times 1.54 \, \text{Å}}{2 \times \sin(20^\circ)} \approx 2.25 \, \text{Å} \]
Bước 4: Kết luận:
Khoảng cách mặt phẳng \(d\) là khoảng \(2.25 \, \text{Å}\).
XEM THÊM:
Bài Tập 4: Phân Tích Cấu Trúc Tinh Thể Từ Kết Quả Nhiễu Xạ
Trong bài tập này, chúng ta sẽ phân tích cấu trúc tinh thể dựa trên kết quả nhiễu xạ tia X. Bài toán yêu cầu xác định các thông số cấu trúc như hệ số mạng, loại tinh thể, và các vị trí nguyên tử trong mạng.
Bước 1: Thu thập dữ liệu nhiễu xạ, bao gồm các góc nhiễu xạ \(\theta\), bậc nhiễu xạ \(n\), và bước sóng tia X \(\lambda\).
Bước 2: Sử dụng phương trình Bragg để tính khoảng cách mặt phẳng \(d\):
\[ d = \frac{n\lambda}{2\sin(\theta)} \]
Bước 3: Dựa trên các khoảng cách mặt phẳng \(d\) và các góc nhiễu xạ, xác định hệ số mạng và loại tinh thể (lập phương, lục giác, v.v.).
Bước 4: Sử dụng các dữ liệu này để xác định vị trí của các nguyên tử trong mạng tinh thể, và từ đó xác định cấu trúc tinh thể cụ thể.
Bước 5: Kết luận về cấu trúc tinh thể dựa trên phân tích dữ liệu.

Bài Tập 5: So Sánh Kết Quả Nhiễu Xạ Giữa Hai Mẫu Vật Khác Nhau
Trong bài tập này, chúng ta sẽ tiến hành so sánh kết quả nhiễu xạ tia X giữa hai mẫu vật khác nhau. Quá trình này giúp xác định các đặc điểm khác biệt về cấu trúc tinh thể, từ đó đưa ra những kết luận quan trọng trong nghiên cứu khoa học và ứng dụng công nghệ.
1. Chuẩn Bị Dữ Liệu Nhiễu Xạ
Đầu tiên, bạn cần thu thập dữ liệu nhiễu xạ tia X của hai mẫu vật. Đảm bảo rằng dữ liệu này bao gồm các giá trị về góc nhiễu xạ \(\theta\), cường độ nhiễu xạ, và các chỉ số tinh thể học liên quan.
2. Phân Tích Dữ Liệu Nhiễu Xạ
Xác định các đỉnh nhiễu xạ chính từ dữ liệu của mỗi mẫu vật.
Tính toán khoảng cách mặt phẳng \[d\] dựa trên phương trình Bragg:
\[ n\lambda = 2d\sin\theta \]So sánh các giá trị \[d\] giữa hai mẫu vật để xác định sự khác biệt về cấu trúc tinh thể.
3. So Sánh Các Đỉnh Nhiễu Xạ
Tiếp theo, hãy so sánh các đỉnh nhiễu xạ giữa hai mẫu vật. Sự khác biệt về vị trí và cường độ của các đỉnh nhiễu xạ có thể chỉ ra các biến đổi về cấu trúc tinh thể giữa hai mẫu.
Nếu các đỉnh nhiễu xạ có vị trí khác nhau, điều này cho thấy sự khác biệt về khoảng cách mặt phẳng tinh thể \[d\].
Sự khác biệt về cường độ của các đỉnh nhiễu xạ có thể phản ánh sự khác nhau về thành phần hoặc cấu trúc vi mô của mẫu vật.
4. Đánh Giá Và Kết Luận
Sau khi so sánh, bạn có thể đưa ra các nhận định về sự khác biệt và giống nhau giữa hai mẫu vật. Điều này có thể giúp xác định mẫu vật nào có cấu trúc tinh thể ổn định hơn hoặc có các đặc tính vật lý khác biệt.
5. Bài Tập Thực Hành
Hãy thử áp dụng phương pháp so sánh trên với các mẫu vật mà bạn có. Ghi lại các kết quả và phân tích sự khác biệt về cấu trúc tinh thể giữa chúng.

Bài Tập 6: Ứng Dụng Phương Trình Bragg Trong Tính Toán Khoảng Cách
Phương trình Bragg là một trong những công cụ quan trọng nhất trong việc phân tích cấu trúc tinh thể thông qua nhiễu xạ tia X. Để tính toán khoảng cách giữa các mặt phẳng nguyên tử trong tinh thể, chúng ta có thể áp dụng phương trình này theo các bước sau:
- Xác định các tham số cần thiết:
- Bước sóng của tia X \(\lambda\) (thường được cung cấp hoặc có thể đo được).
- Góc nhiễu xạ \(\theta\) (góc giữa tia tới và mặt phẳng nhiễu xạ).
- Thứ tự của vết nhiễu xạ \(n\) (thường là bậc nhất, tức là \(n = 1\)).
- Áp dụng phương trình Bragg: Phương trình Bragg có dạng:
\[
n\lambda = 2d\sin(\theta)
\]
Trong đó:
- \(n\) là số nguyên dương (bậc của vết nhiễu xạ).
- \(\lambda\) là bước sóng của tia X.
- \(d\) là khoảng cách giữa các mặt phẳng nguyên tử trong tinh thể.
- \(\theta\) là góc nhiễu xạ.
- Tính toán khoảng cách \(d\): Từ phương trình trên, ta có thể dễ dàng tính được khoảng cách \(d\) giữa các mặt phẳng trong tinh thể: \[ d = \frac{n\lambda}{2\sin(\theta)} \]
- Áp dụng vào bài tập cụ thể: Với các giá trị thực tế của \(\lambda\), \(\theta\), và \(n\), bạn có thể thay vào phương trình để tính khoảng cách \(d\). Ví dụ, nếu bước sóng \(\lambda = 0.154\) nm, góc nhiễu xạ \(\theta = 30^\circ\), và \(n = 1\), khoảng cách \(d\) sẽ được tính như sau: \[ d = \frac{1 \times 0.154}{2\sin(30^\circ)} = 0.154 \, \text{nm} \]
- Kết luận: Phương trình Bragg không chỉ giúp xác định khoảng cách giữa các mặt phẳng nguyên tử mà còn là công cụ quan trọng trong việc hiểu sâu hơn về cấu trúc tinh thể và các đặc tính vật lý liên quan.
Bài Tập 7: Xác Định Thông Số Cấu Trúc Từ Dữ Liệu Nhiễu Xạ
Trong bài tập này, chúng ta sẽ học cách xác định các thông số cấu trúc từ dữ liệu nhiễu xạ tia X. Đây là một kỹ năng quan trọng trong lĩnh vực vật lý và hóa học, đặc biệt là trong nghiên cứu tinh thể học. Chúng ta sẽ sử dụng dữ liệu thu được từ thí nghiệm nhiễu xạ tia X để tính toán các thông số như khoảng cách giữa các mặt phẳng nguyên tử, góc nhiễu xạ, và hệ số phản xạ.
- Bước 1: Xác định các đỉnh nhiễu xạ từ dữ liệu thí nghiệm.
- Bước 2: Sử dụng phương trình Bragg để tính toán khoảng cách giữa các mặt phẳng nguyên tử trong tinh thể:
\[
n\lambda = 2d\sin(\theta)
\]
Trong đó:
- \(\lambda\) là bước sóng của tia X.
- \(\theta\) là góc nhiễu xạ.
- \(d\) là khoảng cách giữa các mặt phẳng nguyên tử.
Bằng cách giải phương trình này, chúng ta có thể xác định khoảng cách \(d\) dựa trên các giá trị \(\lambda\) và \(\theta\) thu được từ thí nghiệm.
- Bước 3: Xác định vị trí và cường độ của các vết nhiễu xạ để xây dựng mô hình cấu trúc tinh thể.
- Bước 4: Áp dụng các phương pháp toán học như biến đổi Fourier để phân tích mô hình cấu trúc tinh thể, xác định vị trí các nguyên tử bên trong tinh thể.
Kết quả cuối cùng là một mô hình chi tiết về sự sắp xếp các nguyên tử trong tinh thể, từ đó có thể suy ra các thông số quan trọng như góc liên kết, độ dài liên kết và mật độ electron.
| Thông số | Giá trị |
| Góc nhiễu xạ \(\theta\) | ... |
| Khoảng cách giữa các mặt phẳng \(d\) | ... |
| Bước sóng \(\lambda\) | ... |
Thông qua bài tập này, chúng ta có thể hiểu rõ hơn về cách thức các dữ liệu nhiễu xạ tia X được sử dụng để xác định các thông số cấu trúc của tinh thể, góp phần vào nghiên cứu và ứng dụng trong các lĩnh vực khoa học vật liệu và hóa học.
Bài Tập 8: Phân Tích Kết Quả Nhiễu Xạ Của Một Hợp Chất Phức Tạp
Trong bài tập này, chúng ta sẽ tiến hành phân tích kết quả nhiễu xạ tia X của một hợp chất phức tạp nhằm xác định các thông số cấu trúc quan trọng. Bài tập được chia thành các bước cụ thể như sau:
- Chuẩn bị dữ liệu nhiễu xạ:
Trước hết, bạn cần có được dữ liệu nhiễu xạ từ thực nghiệm, thường là dưới dạng phổ nhiễu xạ tia X. Các dữ liệu này sẽ cho bạn biết sự phân bố cường độ nhiễu xạ theo góc tán xạ (2θ).
- Xác định các cực đại nhiễu xạ:
Xác định các vị trí góc của các cực đại nhiễu xạ trong phổ. Những vị trí này tương ứng với các mặt phẳng tinh thể khác nhau trong cấu trúc của hợp chất.
- Áp dụng phương trình Bragg:
Sử dụng phương trình Bragg \(\[n\lambda = 2d\sin\theta\]\) để tính toán khoảng cách giữa các mặt phẳng tinh thể (\(d\)) cho từng cực đại nhiễu xạ, trong đó:
- \(n\) là bậc của nhiễu xạ (thường là 1).
- \(\lambda\) là bước sóng của tia X sử dụng.
- \(\theta\) là góc nhiễu xạ tương ứng với cực đại.
- Phân tích cấu trúc:
Sau khi có được các giá trị \(d\), bạn tiến hành phân tích để xác định cấu trúc của hợp chất. Điều này bao gồm so sánh với các giá trị chuẩn hoặc sử dụng các mô hình cấu trúc đã biết để suy ra các thông số cấu trúc như kích thước ô đơn vị, loại mạng tinh thể, và vị trí nguyên tử trong ô đơn vị.
- Kiểm tra và đối chiếu:
Cuối cùng, so sánh các kết quả tính toán với các dữ liệu đã công bố hoặc các tài liệu tham khảo để xác nhận tính chính xác của phân tích.
Bài tập này không chỉ giúp bạn nắm vững các bước phân tích nhiễu xạ tia X mà còn cung cấp cơ hội để thực hành cách áp dụng các công thức và phương pháp trong vật lý học để giải quyết các vấn đề thực tiễn.
Bài Tập 9: Tính Góc Nhiễu Xạ Cho Các Bước Sóng Khác Nhau
Trong bài tập này, chúng ta sẽ tiến hành tính toán góc nhiễu xạ cho các bước sóng khác nhau bằng cách sử dụng phương trình Bragg, công thức nổi tiếng trong lĩnh vực nhiễu xạ tia X. Phương trình này giúp xác định mối quan hệ giữa bước sóng \(\lambda\), khoảng cách mặt phẳng tinh thể \(d\), và góc nhiễu xạ \(\theta\).
- Xác định thông số ban đầu:
- Bước sóng của tia X: \(\lambda\)
- Khoảng cách giữa các mặt phẳng trong tinh thể: \(d\)
- Áp dụng phương trình Bragg:
Phương trình Bragg được biểu diễn như sau:
\[ n\lambda = 2d\sin\theta \]
Trong đó:
- \(n\) là số nguyên chỉ số bậc nhiễu xạ (thường lấy giá trị \(n = 1\) cho trường hợp cơ bản)
- \(\lambda\) là bước sóng của tia X
- \(d\) là khoảng cách giữa các mặt phẳng trong mạng tinh thể
- \(\theta\) là góc nhiễu xạ
- Tính toán góc nhiễu xạ \(\theta\) cho các bước sóng khác nhau:
- Với mỗi bước sóng \(\lambda_1, \lambda_2, \ldots, \lambda_n\), sử dụng phương trình Bragg để giải cho góc \(\theta\).
- Kết quả sẽ là các góc \(\theta_1, \theta_2, \ldots, \theta_n\) tương ứng với các bước sóng đã cho.
- Phân tích kết quả:
So sánh các góc nhiễu xạ đã tính được để xác định mối quan hệ giữa bước sóng và góc nhiễu xạ. Thông thường, khi bước sóng \(\lambda\) tăng, góc nhiễu xạ \(\theta\) cũng tăng theo, nhưng điều này cần được kiểm chứng thông qua tính toán cụ thể.
Thông qua bài tập này, bạn sẽ nắm vững cách sử dụng phương trình Bragg trong thực hành để tính toán góc nhiễu xạ, từ đó hiểu rõ hơn về tính chất của vật liệu thông qua phương pháp nhiễu xạ tia X.
Bài Tập 10: Ứng Dụng Nhiễu Xạ Tia X Trong Xác Định Thành Phần Hóa Học
Trong bài tập này, chúng ta sẽ tìm hiểu cách ứng dụng phương pháp nhiễu xạ tia X để xác định thành phần hóa học của một chất rắn. Phương pháp này dựa trên hiện tượng nhiễu xạ của các tia X khi chúng tương tác với các mặt phẳng nguyên tử trong tinh thể, từ đó tạo ra các mẫu nhiễu xạ đặc trưng.
1. Nguyên Lý Cơ Bản
Phương pháp nhiễu xạ tia X cho phép xác định cấu trúc tinh thể của một chất dựa trên sự giao thoa của các tia X sau khi đi qua một mẫu tinh thể. Dựa vào vị trí và cường độ của các vết nhiễu xạ, chúng ta có thể suy ra vị trí của các nguyên tử và cấu trúc không gian của chất đó.
2. Các Bước Thực Hiện
- Chuẩn bị mẫu: Mẫu cần phân tích phải được tinh thể hóa để có cấu trúc sắp xếp có trật tự. Điều này là cần thiết để tạo ra các vết nhiễu xạ rõ ràng và có ý nghĩa.
- Thu thập dữ liệu: Đặt mẫu tinh thể vào thiết bị đo góc (goniometer) và chiếu tia X vào. Mẫu sẽ được quay từ từ để thu thập dữ liệu từ nhiều góc độ khác nhau.
- Phân tích dữ liệu: Sử dụng các mô hình toán học, cụ thể là phép biến đổi Fourier, để chuyển đổi các mẫu nhiễu xạ 2D thành mô hình 3D về mật độ electron trong tinh thể. Dữ liệu này sẽ được kết hợp với thông tin hóa học đã biết để xác định vị trí các nguyên tử trong tinh thể.
3. Tính Toán Góc Nhiễu Xạ
Góc nhiễu xạ \(\theta\) có thể được tính bằng công thức Bragg:
Trong đó:
- \(n\) là bậc của vết nhiễu xạ (thường là 1).
- \(\lambda\) là bước sóng của tia X.
- \(d\) là khoảng cách giữa các mặt phẳng nguyên tử trong tinh thể.
- \(\theta\) là góc nhiễu xạ cần xác định.
Dựa vào công thức này, ta có thể xác định góc nhiễu xạ cho các bước sóng khác nhau bằng cách thay đổi các giá trị \(d\) và \(\lambda\) tương ứng.
4. Ứng Dụng Trong Xác Định Thành Phần Hóa Học
Kết quả của quá trình phân tích nhiễu xạ tia X không chỉ giúp xác định cấu trúc tinh thể mà còn cung cấp thông tin về thành phần hóa học của mẫu. Bằng cách phân tích mật độ electron và so sánh với dữ liệu hóa học đã biết, ta có thể xác định được vị trí các nguyên tử cụ thể trong cấu trúc tinh thể, từ đó suy ra thành phần hóa học của chất.
5. Kết Luận
Phương pháp nhiễu xạ tia X là một công cụ mạnh mẽ trong việc phân tích cấu trúc và thành phần hóa học của vật liệu. Bài tập này không chỉ giúp bạn hiểu rõ hơn về nguyên lý nhiễu xạ mà còn mở ra nhiều ứng dụng thực tiễn trong nghiên cứu và phát triển vật liệu mới.
.pdf/nhieu-xa-tia-x-(xrd).pdf-0.jpg)