Chủ đề giao thoa là gì: Giao thoa là một hiện tượng sóng quan trọng trong vật lý, thể hiện tính chất sóng của ánh sáng và âm thanh. Bài viết này sẽ giúp bạn khám phá sâu hơn về hiện tượng giao thoa, các ứng dụng của nó trong đời sống, và những thí nghiệm nổi bật minh chứng cho tính chất sóng trong tự nhiên.
Mục lục
- Giao Thoa Là Gì?
- I. Khái Niệm Giao Thoa
- II. Bài Tập Về Giao Thoa Ánh Sáng (Có Lời Giải)
- 1. Bài Tập Tính Khoảng Vân Trong Giao Thoa Ánh Sáng
- 2. Bài Tập Xác Định Bước Sóng Của Ánh Sáng Qua Giao Thoa
- 3. Bài Tập Tính Khoảng Cách Giữa Các Vân Sáng
- 4. Bài Tập Về Giao Thoa Ánh Sáng Qua Hai Khe
- 5. Bài Tập Xác Định Vị Trí Các Vân Sáng Và Tối
- 6. Bài Tập Tính Độ Lệch Pha Trong Giao Thoa Ánh Sáng
- 7. Bài Tập Xác Định Tần Số Sóng Qua Giao Thoa Ánh Sáng
- 8. Bài Tập Về Giao Thoa Ánh Sáng Trong Môi Trường Khác Nhau
- 9. Bài Tập Tính Cường Độ Sáng Của Các Vân Giao Thoa
- 10. Bài Tập Tính Số Vân Sáng Tối Trên Màn
- III. Bài Tập Về Giao Thoa Sóng Âm (Có Lời Giải)
- 1. Bài Tập Tính Tần Số Cộng Hưởng Trong Giao Thoa Sóng Âm
- 2. Bài Tập Xác Định Vị Trí Các Điểm Cực Đại Âm Thanh
- 3. Bài Tập Tính Độ Lệch Pha Trong Giao Thoa Sóng Âm
- 4. Bài Tập Xác Định Cường Độ Âm Qua Giao Thoa
- 5. Bài Tập Về Giao Thoa Sóng Âm Qua Hai Nguồn Phát
- 6. Bài Tập Tính Khoảng Cách Giữa Các Vùng Âm Yếu
- 7. Bài Tập Xác Định Sự Triệt Tiêu Của Sóng Âm
- 8. Bài Tập Về Giao Thoa Sóng Âm Trong Không Khí
- 9. Bài Tập Xác Định Khoảng Cách Giữa Các Nút Sóng Âm
- 10. Bài Tập Tính Số Lần Cộng Hưởng Trong Một Chu Kỳ
Giao Thoa Là Gì?
Giao thoa là hiện tượng xảy ra khi hai hay nhiều sóng gặp nhau và tương tác với nhau, tạo ra một sóng mới. Hiện tượng này có thể xảy ra với các loại sóng như sóng cơ, sóng âm, và sóng ánh sáng.
Giao Thoa Ánh Sáng
Giao thoa ánh sáng là một trong những hiện tượng nổi bật của vật lý, minh chứng cho tính chất sóng của ánh sáng. Thí nghiệm nổi tiếng nhất minh họa cho hiện tượng này là thí nghiệm của Thomas Young. Trong thí nghiệm này, ánh sáng được chiếu qua hai khe hẹp và tạo ra các vân sáng và tối xen kẽ trên màn hình quan sát, chứng tỏ ánh sáng có tính chất sóng.
Điều kiện để xảy ra giao thoa ánh sáng:
- Các nguồn sáng phải kết hợp, tức là có cùng tần số và độ lệch pha không đổi.
- Khoảng cách giữa hai khe phải rất nhỏ so với khoảng cách từ hai khe đến màn quan sát.
Các vân sáng và tối trên màn hình tạo ra một mô hình giao thoa, và khoảng cách giữa các vân được gọi là khoảng vân, được tính bằng công thức:
\[ i = \frac{\lambda D}{a} \]
Trong đó:
- \(\lambda\) là bước sóng ánh sáng.
- \(D\) là khoảng cách từ hai khe đến màn quan sát.
- \(a\) là khoảng cách giữa hai khe.
Ứng Dụng Của Hiện Tượng Giao Thoa
Hiện tượng giao thoa ánh sáng có nhiều ứng dụng trong thực tế, như:
- Đo bước sóng ánh sáng.
- Ứng dụng trong các thiết bị quang học như kính hiển vi và kính thiên văn.
- Phát triển các công nghệ hình ảnh y khoa và các thiết bị đo lường chính xác.
Giao Thoa Sóng Âm
Giao thoa cũng xảy ra với sóng âm, khi hai hay nhiều sóng âm gặp nhau, chúng có thể cộng hưởng hoặc triệt tiêu lẫn nhau, tạo ra các âm thanh to hoặc yếu hơn. Hiện tượng này được ứng dụng trong kỹ thuật âm thanh để điều chỉnh âm lượng và chất lượng âm thanh.
Kết Luận
Giao thoa là một hiện tượng vật lý cơ bản, thể hiện tính chất sóng của các loại sóng trong tự nhiên. Từ giao thoa ánh sáng đến giao thoa sóng âm, hiện tượng này không chỉ giúp chúng ta hiểu rõ hơn về thế giới tự nhiên mà còn mang lại nhiều ứng dụng thiết thực trong khoa học và công nghệ.

.png)
I. Khái Niệm Giao Thoa
Giao thoa là một hiện tượng xảy ra khi hai hay nhiều sóng gặp nhau, tạo ra một sóng mới có biên độ phụ thuộc vào sự kết hợp của các sóng ban đầu. Hiện tượng này thường được quan sát trong các loại sóng như sóng âm, sóng ánh sáng, và sóng nước.
Các loại giao thoa chính gồm:
- Giao thoa tăng cường: Xảy ra khi các sóng gặp nhau tại cùng một pha, làm tăng biên độ tổng hợp của sóng.
- Giao thoa triệt tiêu: Xảy ra khi các sóng gặp nhau tại các pha đối ngược, làm giảm biên độ hoặc triệt tiêu hoàn toàn sóng.
Trong thực tế, giao thoa ánh sáng là một trong những hiện tượng nổi bật, minh chứng cho tính chất sóng của ánh sáng. Điều này có thể được biểu diễn qua thí nghiệm khe đôi của Young, nơi các vân sáng và tối xuất hiện trên màn, minh họa cho sự giao thoa giữa các sóng ánh sáng.
Toán học miêu tả giao thoa thông qua sự chồng chập của các hàm sóng. Nếu hai sóng có phương trình dạng:
Thì sóng tổng hợp sẽ có dạng:
Trong đó, \( A \) và \( \phi \) phụ thuộc vào \( A_1 \), \( A_2 \), \( \phi_1 \), và \( \phi_2 \), quyết định biên độ và pha của sóng tổng hợp.
II. Bài Tập Về Giao Thoa Ánh Sáng (Có Lời Giải)
Dưới đây là một số bài tập về hiện tượng giao thoa ánh sáng, kèm theo lời giải chi tiết để bạn tham khảo:
- Bài tập 1: Hai khe Young cách nhau một khoảng \(d = 0,5 \, mm\) chiếu ánh sáng đơn sắc có bước sóng \(\lambda = 600 \, nm\). Tính khoảng cách giữa các vân sáng liên tiếp trên màn cách hai khe một khoảng \(L = 2 \, m\).
- Bài tập 2: Trong thí nghiệm Young, ánh sáng có bước sóng \( \lambda_1 = 500 \, nm\) và \( \lambda_2 = 650 \, nm\) chiếu qua hai khe. Tính khoảng vân và số vân sáng trùng nhau trong phạm vi rộng 1cm.
- Bài tập 3: Trong thí nghiệm giao thoa ánh sáng với khe Young, nếu thay đổi khoảng cách giữa hai khe từ \(d_1\) sang \(d_2\), thì số vân sáng trên màn sẽ thay đổi như thế nào?
- Bài tập 4: Một nguồn sáng đơn sắc phát ra ánh sáng có bước sóng \( \lambda = 700 \, nm\) chiếu vào hai khe cách nhau \(0,3 \, mm\). Xác định vị trí vân sáng bậc 3 trên màn cách khe một khoảng \(2 \, m\).
- Bài tập 5: Ánh sáng có bước sóng \( \lambda = 550 \, nm\) tạo ra vân giao thoa trên màn cách khe một khoảng \(3 \, m\). Biết khoảng cách giữa hai khe là \(0,4 \, mm\). Tính số vân sáng trong đoạn \(10 \, cm\) trên màn.
Lời giải:
Khoảng cách giữa hai vân sáng liên tiếp được tính bằng công thức:
\[ \Delta y = \frac{\lambda L}{d} = \frac{600 \times 10^{-9} \times 2}{0,5 \times 10^{-3}} = 2,4 \, mm \]Lời giải:
Khoảng vân cho mỗi bước sóng là:
\[ \Delta y_1 = \frac{\lambda_1 L}{d}, \quad \Delta y_2 = \frac{\lambda_2 L}{d} \]Số vân sáng trùng nhau được tính bằng cách tìm bội chung nhỏ nhất của \( \Delta y_1 \) và \( \Delta y_2 \).
Lời giải:
Khoảng vân được tính bằng công thức:
\[ \Delta y = \frac{\lambda L}{d} \]Nếu \(d\) tăng thì \( \Delta y \) sẽ giảm và số vân sáng tăng lên. Ngược lại, nếu \(d\) giảm thì \( \Delta y \) tăng và số vân sáng giảm đi.
Lời giải:
Vị trí của vân sáng bậc \(k\) được tính bằng công thức:
\[ y_k = k \cdot \frac{\lambda L}{d} = 3 \cdot \frac{700 \times 10^{-9} \times 2}{0,3 \times 10^{-3}} = 14 \, mm \]Lời giải:
Khoảng cách giữa các vân sáng là:
\[ \Delta y = \frac{\lambda L}{d} = \frac{550 \times 10^{-9} \times 3}{0,4 \times 10^{-3}} = 4,125 \, mm \]Số vân sáng trong đoạn \(10 \, cm\) là:
\[ n = \frac{100 \, mm}{\Delta y} = \frac{100}{4,125} \approx 24 \, vân \]
1. Bài Tập Tính Khoảng Vân Trong Giao Thoa Ánh Sáng
Dưới đây là một số bài tập giúp bạn rèn luyện khả năng tính toán khoảng vân trong hiện tượng giao thoa ánh sáng. Các bài tập này sẽ hướng dẫn từng bước để giúp bạn hiểu rõ hơn về cách áp dụng công thức.
- Bài tập 1: Hai khe Young cách nhau một khoảng \(d = 0,5 \, mm\), chiếu ánh sáng đơn sắc có bước sóng \(\lambda = 600 \, nm\). Tính khoảng cách giữa các vân sáng liên tiếp trên màn cách hai khe một khoảng \(L = 2 \, m\).
- Bài tập 2: Trong thí nghiệm Young, ánh sáng có bước sóng \(\lambda = 500 \, nm\) chiếu qua hai khe cách nhau \(d = 0,2 \, mm\). Màn quan sát cách hai khe \(L = 1,5 \, m\). Tính khoảng vân giao thoa.
- Bài tập 3: Một nguồn sáng đơn sắc có bước sóng \(\lambda = 700 \, nm\) chiếu vào hai khe Young cách nhau \(0,4 \, mm\). Màn quan sát đặt cách khe một khoảng \(L = 2 \, m\). Tính khoảng cách giữa hai vân sáng liên tiếp.
- Bài tập 4: Trong thí nghiệm giao thoa ánh sáng với hai khe Young, nếu khoảng cách giữa hai khe \(d\) tăng gấp đôi, khoảng vân sẽ thay đổi như thế nào?
- Bài tập 5: Ánh sáng có bước sóng \(\lambda = 550 \, nm\) tạo ra vân giao thoa trên màn cách khe một khoảng \(3 \, m\). Biết khoảng cách giữa hai khe là \(0,5 \, mm\). Tính khoảng cách giữa hai vân sáng liên tiếp.
Giải:
Sử dụng công thức tính khoảng vân \( \Delta y = \frac{\lambda L}{d} \), ta có:
\[ \Delta y = \frac{600 \times 10^{-9} \times 2}{0,5 \times 10^{-3}} = 2,4 \, mm \]Giải:
Sử dụng công thức \( \Delta y = \frac{\lambda L}{d} \), ta có:
\[ \Delta y = \frac{500 \times 10^{-9} \times 1,5}{0,2 \times 10^{-3}} = 3,75 \, mm \]Giải:
Khoảng vân được tính bằng:
\[ \Delta y = \frac{\lambda L}{d} = \frac{700 \times 10^{-9} \times 2}{0,4 \times 10^{-3}} = 3,5 \, mm \]Giải:
Khi khoảng cách \(d\) tăng gấp đôi, khoảng vân \( \Delta y \) sẽ giảm đi một nửa, vì \( \Delta y \) tỉ lệ nghịch với \(d\).
Giải:
Khoảng cách giữa hai vân sáng liên tiếp được tính bằng công thức:
\[ \Delta y = \frac{\lambda L}{d} = \frac{550 \times 10^{-9} \times 3}{0,5 \times 10^{-3}} = 3,3 \, mm \]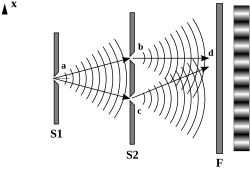
2. Bài Tập Xác Định Bước Sóng Của Ánh Sáng Qua Giao Thoa
Dưới đây là các bài tập giúp bạn thực hành xác định bước sóng của ánh sáng dựa trên hiện tượng giao thoa. Mỗi bài tập sẽ được hướng dẫn chi tiết, từng bước để giúp bạn nắm rõ cách tính toán.
- Bài tập 1: Trong thí nghiệm Young, khoảng cách giữa hai khe là \(d = 0,6 \, mm\), khoảng cách từ khe đến màn là \(L = 1,5 \, m\), khoảng vân đo được là \( \Delta y = 2 \, mm\). Tính bước sóng của ánh sáng sử dụng trong thí nghiệm.
- Bài tập 2: Một thí nghiệm giao thoa ánh sáng sử dụng hai khe hẹp với khoảng cách \(d = 0,3 \, mm\). Màn quan sát đặt cách hai khe \(L = 2 \, m\), khoảng vân đo được là \( \Delta y = 4 \, mm\). Tính bước sóng của ánh sáng.
- Bài tập 3: Trong một thí nghiệm, bước sóng ánh sáng \( \lambda \) cần được xác định. Khoảng cách giữa hai khe là \(d = 0,4 \, mm\), khoảng cách từ khe đến màn là \(L = 1 \, m\), và khoảng vân đo được là \( \Delta y = 5 \, mm\). Xác định bước sóng ánh sáng.
- Bài tập 4: Trong thí nghiệm Young với khoảng cách giữa hai khe là \(d = 0,5 \, mm\), ánh sáng có bước sóng cần tìm. Màn quan sát đặt cách hai khe \(L = 2,5 \, m\) và khoảng vân đo được là \( \Delta y = 1 \, mm\). Tính bước sóng của ánh sáng.
- Bài tập 5: Ánh sáng đơn sắc có bước sóng cần tìm trong thí nghiệm Young, với khoảng cách giữa hai khe là \(d = 0,7 \, mm\), khoảng cách từ khe đến màn là \(L = 3 \, m\), và khoảng vân đo được là \( \Delta y = 3,5 \, mm\). Xác định bước sóng của ánh sáng.
Giải:
Sử dụng công thức \( \Delta y = \frac{\lambda L}{d} \), ta có:
\[ \lambda = \frac{\Delta y \cdot d}{L} = \frac{2 \times 10^{-3} \times 0,6 \times 10^{-3}}{1,5} = 800 \, nm \]Giải:
Theo công thức \( \Delta y = \frac{\lambda L}{d} \), bước sóng ánh sáng được tính là:
\[ \lambda = \frac{\Delta y \cdot d}{L} = \frac{4 \times 10^{-3} \times 0,3 \times 10^{-3}}{2} = 600 \, nm \]Giải:
Sử dụng công thức xác định bước sóng:
\[ \lambda = \frac{\Delta y \cdot d}{L} = \frac{5 \times 10^{-3} \times 0,4 \times 10^{-3}}{1} = 2000 \, nm \]Giải:
Công thức xác định bước sóng là:
\[ \lambda = \frac{\Delta y \cdot d}{L} = \frac{1 \times 10^{-3} \times 0,5 \times 10^{-3}}{2,5} = 200 \, nm \]Giải:
Bước sóng ánh sáng được tính như sau:
\[ \lambda = \frac{\Delta y \cdot d}{L} = \frac{3,5 \times 10^{-3} \times 0,7 \times 10^{-3}}{3} = 816,67 \, nm \]
3. Bài Tập Tính Khoảng Cách Giữa Các Vân Sáng
Trong thí nghiệm giao thoa ánh sáng, khoảng cách giữa các vân sáng (hay còn gọi là khoảng vân) là một trong những yếu tố quan trọng để xác định tính chất sóng của ánh sáng. Dưới đây là các bước tính toán khoảng cách giữa các vân sáng trong thí nghiệm:
- Xác định các thông số ban đầu:
- Khoảng cách giữa hai khe hẹp: \( a \)
- Khoảng cách từ hai khe đến màn: \( D \)
- Bước sóng của ánh sáng đơn sắc: \( \lambda \)
- Sử dụng công thức tính khoảng vân:
Công thức tính khoảng cách giữa hai vân sáng liên tiếp:
\[ i = \frac{\lambda D}{a} \]Trong đó:
- \( i \) là khoảng vân (khoảng cách giữa hai vân sáng liên tiếp).
- \( \lambda \) là bước sóng của ánh sáng.
- \( D \) là khoảng cách từ hai khe đến màn.
- \( a \) là khoảng cách giữa hai khe hẹp.
- Áp dụng vào bài toán cụ thể:
Giả sử, chúng ta có các giá trị sau:
- Bước sóng ánh sáng \( \lambda = 600 \, \text{nm} \) (nanomet).
- Khoảng cách giữa hai khe \( a = 0.5 \, \text{mm} \) (milimet).
- Khoảng cách từ khe đến màn \( D = 1.5 \, \text{m} \) (met).
Khi đó, khoảng cách giữa hai vân sáng liên tiếp được tính như sau:
\[ i = \frac{600 \times 10^{-9} \times 1.5}{0.5 \times 10^{-3}} = 1.8 \, \text{mm} \]Vậy, khoảng cách giữa các vân sáng là 1.8 mm.
- Kết luận:
Bằng cách sử dụng công thức trên, chúng ta có thể dễ dàng tính được khoảng cách giữa các vân sáng trong thí nghiệm giao thoa ánh sáng, giúp hiểu rõ hơn về tính chất sóng của ánh sáng.
XEM THÊM:
4. Bài Tập Về Giao Thoa Ánh Sáng Qua Hai Khe
Bài tập giao thoa ánh sáng qua hai khe là một trong những dạng bài tập phổ biến trong chương trình Vật Lý. Dưới đây là hướng dẫn giải chi tiết:
- Đề bài:
Cho hai khe hẹp cách nhau một khoảng \(a\). Chiếu ánh sáng đơn sắc có bước sóng \( \lambda \) từ phía trước hai khe. Khoảng cách từ hai khe đến màn quan sát là \(D\). Tính khoảng cách giữa các vân sáng liên tiếp trên màn.
- Phân tích:
Trong hiện tượng giao thoa qua hai khe, các vân sáng và vân tối xuất hiện do sự giao thoa giữa các sóng ánh sáng phát ra từ hai khe. Khoảng cách giữa hai vân sáng liên tiếp (khoảng vân) được xác định bởi công thức:
\[ i = \frac{\lambda D}{a} \] - Áp dụng công thức:
Giả sử bước sóng ánh sáng là \( \lambda = 600 \, \text{nm} \), khoảng cách giữa hai khe là \( a = 0.5 \, \text{mm} \), và khoảng cách từ hai khe đến màn là \( D = 2 \, \text{m} \). Khi đó:
\[ i = \frac{600 \times 10^{-9} \times 2}{0.5 \times 10^{-3}} = 2.4 \, \text{mm} \]Khoảng cách giữa hai vân sáng liên tiếp là 2.4 mm.
- Kết luận:
Thông qua công thức và cách tính trên, ta có thể dễ dàng xác định được khoảng cách giữa các vân sáng trong thí nghiệm giao thoa ánh sáng qua hai khe, một hiện tượng minh chứng rõ ràng cho bản chất sóng của ánh sáng.

5. Bài Tập Xác Định Vị Trí Các Vân Sáng Và Tối
Trong hiện tượng giao thoa ánh sáng, các vân sáng và vân tối xuất hiện do sự kết hợp của các sóng ánh sáng từ hai nguồn sáng kết hợp. Để xác định vị trí các vân này, ta sử dụng các công thức toán học dựa trên nguyên lý giao thoa của sóng.
Công thức xác định vị trí vân sáng:
Vị trí các vân sáng được xác định theo công thức:
\[ y_m = \left( m \cdot \dfrac{\lambda \cdot D}{a} \right) \]
Trong đó:
- \( y_m \): vị trí của vân sáng thứ \( m \)
- \( m \): số nguyên (0, ±1, ±2, ...), tương ứng với các vân sáng trung tâm và các vân sáng bậc 1, bậc 2, ...
- \( \lambda \): bước sóng của ánh sáng sử dụng
- \( D \): khoảng cách từ hai khe đến màn quan sát
- \( a \): khoảng cách giữa hai khe sáng
Công thức xác định vị trí vân tối:
Vị trí các vân tối nằm giữa hai vân sáng liên tiếp và được xác định bởi công thức:
\[ y_t = \left( \left( m + \dfrac{1}{2} \right) \cdot \dfrac{\lambda \cdot D}{a} \right) \]
Trong đó:
- \( y_t \): vị trí của vân tối
- Các ký hiệu khác tương tự như trên.
Ví dụ bài tập:
Xác định vị trí các vân sáng và vân tối trong một thí nghiệm giao thoa ánh sáng với các thông số sau:
- Bước sóng ánh sáng \( \lambda = 600 \, \text{nm} \).
- Khoảng cách giữa hai khe \( a = 1 \, \text{mm} \).
- Khoảng cách từ khe đến màn \( D = 2 \, \text{m} \).
Lời giải:
Vị trí các vân sáng thứ \( m = 1, 2, 3, ... \) được tính theo công thức:
\[ y_m = \dfrac{m \cdot 600 \times 10^{-9} \times 2}{1 \times 10^{-3}} \]
\[ y_m = m \times 1.2 \times 10^{-3} \, \text{m} = m \times 1.2 \, \text{mm} \]
Vị trí vân sáng thứ nhất (\( m = 1 \)) sẽ là \( y_1 = 1.2 \, \text{mm} \), vân sáng thứ hai (\( m = 2 \)) sẽ là \( y_2 = 2.4 \, \text{mm} \), và tiếp tục như vậy.
Vị trí các vân tối nằm giữa các vân sáng, được xác định bởi công thức:
\[ y_t = \left( m + \dfrac{1}{2} \right) \times 1.2 \, \text{mm} \]
Ví dụ, vân tối đầu tiên nằm tại vị trí \( y_t = 0.6 \, \text{mm} \), giữa vân sáng trung tâm và vân sáng thứ nhất.

6. Bài Tập Tính Độ Lệch Pha Trong Giao Thoa Ánh Sáng
Độ lệch pha trong giao thoa ánh sáng là một đại lượng quan trọng giúp xác định sự khác biệt về pha của hai sóng ánh sáng tại một điểm trên màn giao thoa. Sau đây là các bước cơ bản để giải một bài tập tính độ lệch pha trong giao thoa ánh sáng:
-
Xác định các thông số cần thiết:
- Khoảng cách giữa hai nguồn sáng \( d \)
- Khoảng cách từ các nguồn đến điểm khảo sát \( d_1 \) và \( d_2 \)
- Bước sóng của ánh sáng \( \lambda \)
- Độ lệch pha ban đầu \( \varphi_0 \) (nếu có)
-
Công thức tính độ lệch pha:
Độ lệch pha giữa hai sóng tại một điểm M trên màn giao thoa được tính theo công thức:
\[ \Delta \varphi = \frac{2\pi (d_2 - d_1)}{\lambda} \]Trong đó:
- \( \Delta \varphi \): Độ lệch pha
- \( d_1, d_2 \): Khoảng cách từ hai nguồn sáng đến điểm M
- \( \lambda \): Bước sóng của ánh sáng
-
Xác định trạng thái giao thoa:
Từ độ lệch pha \( \Delta \varphi \), ta có thể xác định được điểm giao thoa là vân sáng hay vân tối:
- Vân sáng: Khi \( \Delta \varphi = 2k\pi \), với \( k \in \mathbb{Z} \)
- Vân tối: Khi \( \Delta \varphi = (2k + 1)\pi \), với \( k \in \mathbb{Z} \)
-
Ví dụ minh họa:
Cho hai nguồn sáng cách nhau một khoảng \( d = 2\ \text{cm} \), bước sóng của ánh sáng là \( \lambda = 500\ \text{nm} \). Tính độ lệch pha tại điểm M cách hai nguồn \( d_1 = 1.5\ \text{cm} \) và \( d_2 = 1.7\ \text{cm} \).
- Khoảng chênh lệch đường đi: \( \Delta d = d_2 - d_1 = 1.7 - 1.5 = 0.2\ \text{cm} \)
- Độ lệch pha: \[ \Delta \varphi = \frac{2\pi \times 0.2}{500 \times 10^{-7}} = 2.51\ \text{rad} \]
Vì \( \Delta \varphi \approx 2.51\ \text{rad} \), điểm M là một vân sáng.
7. Bài Tập Xác Định Tần Số Sóng Qua Giao Thoa Ánh Sáng
Để xác định tần số sóng qua hiện tượng giao thoa ánh sáng, chúng ta có thể sử dụng công thức liên quan đến bước sóng và vận tốc ánh sáng. Dưới đây là hướng dẫn chi tiết từng bước thực hiện.
- Xác định bước sóng \( \lambda \):
- \( i \): Khoảng vân, là khoảng cách giữa hai vân sáng liên tiếp.
- \( D \): Khoảng cách từ các khe giao thoa đến màn quan sát.
- \( a \): Khoảng cách giữa hai khe giao thoa.
- Tính tần số sóng \( f \):
- \( f \): Tần số của sóng ánh sáng.
- \( c = 3 \times 10^8 \, m/s \): Vận tốc ánh sáng trong chân không.
- \( \lambda \): Bước sóng đã tính được từ bước 1.
- Ví dụ bài tập:
Bước sóng có thể được tính thông qua công thức của khoảng vân:
\[
i = \frac{\lambda D}{a}
\]
Trong đó:
Khi đã có giá trị của khoảng vân \( i \), bước sóng \( \lambda \) có thể được tính theo công thức trên.
Áp dụng công thức liên hệ giữa bước sóng \( \lambda \), vận tốc ánh sáng \( c \), và tần số \( f \):
\[
f = \frac{c}{\lambda}
\]
Trong đó:
Bằng cách thay giá trị \( \lambda \) vào công thức, ta sẽ tính được tần số của sóng ánh sáng.
Giả sử bước sóng \( \lambda = 500 \, nm \), ta có thể tính tần số sóng như sau:
\[
f = \frac{3 \times 10^8}{500 \times 10^{-9}} = 6 \times 10^{14} \, Hz
\]
Vậy tần số sóng ánh sáng là \( 6 \times 10^{14} \, Hz \).

8. Bài Tập Về Giao Thoa Ánh Sáng Trong Môi Trường Khác Nhau
Giao thoa ánh sáng trong các môi trường khác nhau là một hiện tượng thú vị trong quang học sóng. Khi ánh sáng truyền qua các môi trường khác nhau, sự thay đổi của chiết suất môi trường sẽ ảnh hưởng đến bước sóng và tần số của sóng ánh sáng, dẫn đến sự thay đổi trong các vân giao thoa.
Dưới đây là một bài tập chi tiết giúp bạn hiểu rõ hơn về hiện tượng giao thoa ánh sáng khi nó truyền qua các môi trường có chiết suất khác nhau.
- Đề bài: Ánh sáng đơn sắc có bước sóng \(\lambda = 600 \, \text{nm}\) truyền qua hai khe song song cách nhau \(d = 0.5 \, \text{mm}\). Khoảng cách từ hai khe đến màn quan sát là \(D = 2 \, \text{m}\). Khi ánh sáng truyền từ không khí vào môi trường nước có chiết suất \(n = 1.33\), hãy xác định vị trí vân sáng và vân tối trên màn quan sát.
- Lời giải:
- Bước 1: Tính bước sóng của ánh sáng trong môi trường nước: \[ \lambda' = \frac{\lambda}{n} = \frac{600 \, \text{nm}}{1.33} \approx 451.13 \, \text{nm} \]
- Bước 2: Sử dụng công thức tính vị trí vân sáng thứ \(m\) (tương tự cho vân tối nhưng thêm điều kiện \( m + \frac{1}{2} \)): \[ y_m = \frac{m \lambda' D}{d} \] với: \[ y_1 = \frac{1 \times 451.13 \times 10^{-9} \, \text{m} \times 2 \, \text{m}}{0.5 \times 10^{-3} \, \text{m}} \approx 1.8045 \, \text{mm} \] Vậy, vị trí vân sáng thứ nhất trên màn quan sát là \(y_1 \approx 1.8 \, \text{mm}\).
- Bước 3: Tính khoảng cách giữa các vân giao thoa (khoảng vân): \[ i = \frac{\lambda' D}{d} = \frac{451.13 \times 10^{-9} \, \text{m} \times 2 \, \text{m}}{0.5 \times 10^{-3} \, \text{m}} \approx 1.8045 \, \text{mm} \] Khoảng cách giữa các vân giao thoa là \(i \approx 1.8 \, \text{mm}\).
Qua bài tập này, chúng ta có thể thấy rằng chiết suất của môi trường ảnh hưởng đến bước sóng của ánh sáng, từ đó thay đổi vị trí các vân giao thoa trên màn quan sát. Khi ánh sáng truyền từ không khí vào môi trường nước, bước sóng ngắn hơn, dẫn đến khoảng cách giữa các vân sáng cũng thu hẹp lại.
9. Bài Tập Tính Cường Độ Sáng Của Các Vân Giao Thoa
Để tính cường độ sáng của các vân giao thoa, ta sử dụng công thức:
Trong đó:
- I là cường độ sáng tại vị trí cần tính
- I_0 là cường độ sáng cực đại
- \Delta \phi là độ lệch pha giữa hai sóng tại vị trí đó
Công thức độ lệch pha giữa hai sóng có thể được tính bằng:
Trong đó:
- \Delta x là hiệu đường đi của hai sóng
- \lambda là bước sóng của ánh sáng
Ví dụ:
Cho hai nguồn sáng kết hợp có bước sóng \( \lambda = 600 nm \), khoảng cách giữa hai nguồn là \(a = 0.5 mm\), khoảng cách từ hai nguồn đến màn là \(D = 1 m\). Tính cường độ sáng tại một điểm trên màn cách vân sáng trung tâm một khoảng \(x = 0.2 mm\).
- Tính hiệu đường đi giữa hai sóng tại vị trí đó: \[ \Delta x = \frac{a \cdot x}{D} = \frac{0.5 \cdot 0.2}{1} = 0.1 mm \]
- Tính độ lệch pha: \[ \Delta \phi = \frac{2\pi \cdot 0.1}{600 \times 10^{-3}} = \frac{\pi}{3} \]
- Tính cường độ sáng: \[ I = I_0 \cos^2 \left( \frac{\pi}{6} \right) = I_0 \cdot \left( \frac{3}{4} \right) \]
Vậy, cường độ sáng tại vị trí đó bằng \( \frac{3}{4} I_0 \).
10. Bài Tập Tính Số Vân Sáng Tối Trên Màn
Trong hiện tượng giao thoa ánh sáng, số lượng vân sáng và vân tối trên màn có thể tính được thông qua các công thức dựa vào hiệu đường đi của hai sóng kết hợp.
Bài toán: Trong một thí nghiệm giao thoa ánh sáng, khoảng cách giữa hai khe \(a = 0,35 \, mm\), khoảng cách từ hai khe đến màn \(D = 1 \, m\), bước sóng ánh sáng \( \lambda = 0,7 \, \mu m\), và bề rộng vùng giao thoa là \(13,5 \, mm\). Hãy tính số lượng vân sáng và vân tối trên màn.
- Xác định khoảng vân \(i\):
- Tính số lượng vân sáng:
- Tính số lượng vân tối:
- Kết luận:
Khoảng vân \(i\) được tính bằng công thức:
\[
i = \frac{\lambda D}{a}
\]
Thay các giá trị vào công thức:
\[
i = \frac{0,7 \times 10^{-6} \times 1}{0,35 \times 10^{-3}} = 2 \, mm
\]
Số vân sáng xuất hiện trên màn có thể được tính bằng công thức:
\[
N_{\text{vân sáng}} = \frac{\text{bề rộng vùng giao thoa}}{i}
\]
Thay các giá trị:
\[
N_{\text{vân sáng}} = \frac{13,5}{2} = 6,75
\]
Do đó, ta có 6 vân sáng quan sát được.
Số lượng vân tối nằm giữa các vân sáng, do đó số vân tối sẽ là \(N_{\text{vân tối}} = N_{\text{vân sáng}} - 1 = 5\).
Trên màn, chúng ta quan sát được 6 vân sáng và 5 vân tối trong vùng giao thoa có bề rộng \(13,5 \, mm\).

III. Bài Tập Về Giao Thoa Sóng Âm (Có Lời Giải)
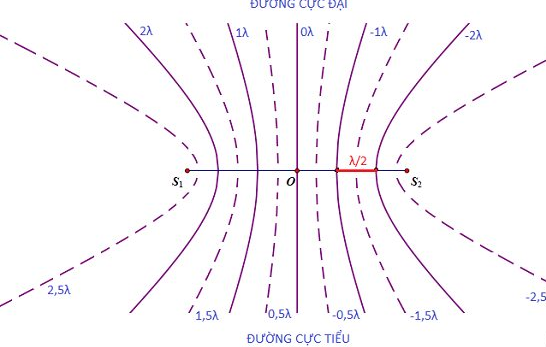
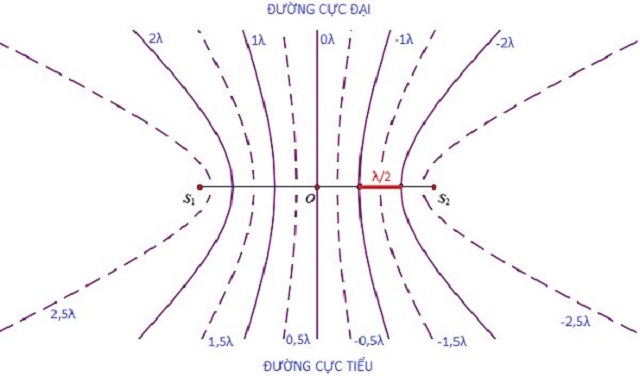
Hiện tượng giao thoa sóng âm xảy ra khi hai nguồn sóng âm kết hợp, tạo ra các vùng dao động mạnh (cực đại) và yếu (cực tiểu) trên không gian. Bài tập về giao thoa sóng âm giúp ta hiểu rõ hơn về sự tương tác giữa các sóng và tính toán vị trí, số lượng các điểm cực đại, cực tiểu trong môi trường truyền âm thanh.
1. Bài Tập Tính Khoảng Cách Giữa Hai Điểm Dao Động Cùng Pha
Cho hai nguồn âm cùng pha \(S_1\) và \(S_2\) dao động tại tần số \(f = 500\) Hz, cách nhau 2 m. Tốc độ truyền âm trong không khí là \(v = 340\) m/s.
- Tính bước sóng \( \lambda \).
- Xác định khoảng cách giữa hai điểm dao động cùng pha nằm trên đường thẳng nối hai nguồn.
Lời giải:
- Bước sóng được tính bằng công thức: \[ \lambda = \frac{v}{f} = \frac{340}{500} = 0.68 \, \text{m} \]
- Điều kiện để hai điểm dao động cùng pha là khoảng cách giữa chúng phải bằng bội số nguyên của bước sóng: \[ \Delta d = k \lambda, \quad k \in \mathbb{Z} \] Do đó, khoảng cách giữa hai điểm dao động cùng pha gần nhau nhất là \(0.68 \, \text{m}\).
2. Bài Tập Tìm Vị Trí Các Điểm Cực Đại
Hai nguồn âm kết hợp \(S_1\) và \(S_2\) phát sóng với bước sóng \(\lambda = 0.5 \, \text{m}\), cách nhau 1.5 m. Xác định vị trí của các điểm cực đại trên đoạn thẳng nối hai nguồn.
Lời giải:
- Điều kiện để có cực đại giao thoa là: \[ \Delta d = k \lambda, \quad k \in \mathbb{Z} \] Với \(\lambda = 0.5 \, \text{m}\) và khoảng cách giữa hai nguồn là \(d = 1.5 \, \text{m}\), ta tìm được số lượng điểm cực đại trên đoạn thẳng nối hai nguồn.
- Điểm cực đại gần nhất cách nguồn thứ nhất một khoảng: \[ \Delta d = 0.5 \, \text{m} \] Do đó, các vị trí cực đại là tại \(d_1 = 0.5 \, \text{m}, d_2 = 1.0 \, \text{m}\).
3. Bài Tập Xác Định Số Điểm Cực Tiểu
Với hai nguồn âm kết hợp cách nhau 1.2 m và bước sóng \( \lambda = 0.4 \, \text{m} \), xác định số điểm cực tiểu giữa hai nguồn.
Lời giải:
- Điều kiện để có cực tiểu là: \[ \Delta d = \left( k + \frac{1}{2} \right) \lambda, \quad k \in \mathbb{Z} \]
- Với \( \lambda = 0.4 \, \text{m} \), ta tính được khoảng cách giữa các điểm cực tiểu là \( 0.2 \, \text{m} \).
1. Bài Tập Tính Tần Số Cộng Hưởng Trong Giao Thoa Sóng Âm
Trong hiện tượng giao thoa sóng âm, tần số cộng hưởng xảy ra khi khoảng cách giữa hai nguồn và môi trường truyền âm tạo ra những điều kiện để sóng giao thoa với nhau theo các bội số nguyên của tần số. Dưới đây là bài tập cụ thể về cách tính tần số cộng hưởng.
Bài tập
Cho hai nguồn âm \( S_1 \) và \( S_2 \) phát ra sóng âm cùng tần số, cách nhau 1.5 m. Tốc độ truyền âm trong không khí là \( v = 340 \, \text{m/s} \). Xác định tần số cộng hưởng khi hai nguồn âm đạt đến cộng hưởng trong không khí.
Lời giải
- Đầu tiên, ta cần tính bước sóng \( \lambda \) của sóng âm khi có cộng hưởng. Điều kiện để có cộng hưởng là khoảng cách giữa hai nguồn âm phải là bội số của bước sóng: \[ d = k \lambda, \quad k \in \mathbb{Z} \] Với \( d = 1.5 \, \text{m} \), ta có: \[ \lambda = \frac{d}{k}, \quad k \in \mathbb{Z} \]
- Từ công thức tính tần số của sóng âm, ta có: \[ f = \frac{v}{\lambda} \] Thay \( \lambda = \frac{d}{k} \) vào, ta được: \[ f = \frac{v \cdot k}{d} = \frac{340 \cdot k}{1.5} \] Tùy theo giá trị của \( k \), ta có thể xác định được tần số cộng hưởng.
Ví dụ, với \( k = 1 \), ta có tần số cộng hưởng đầu tiên là:
\[
f_1 = \frac{340}{1.5} \approx 226.67 \, \text{Hz}
\]
Với \( k = 2 \), tần số cộng hưởng thứ hai là:
\[
f_2 = \frac{340 \cdot 2}{1.5} \approx 453.33 \, \text{Hz}
\]
Do đó, các tần số cộng hưởng của hệ thống là các bội số nguyên của \( 226.67 \, \text{Hz} \).
2. Bài Tập Xác Định Vị Trí Các Điểm Cực Đại Âm Thanh
Trong giao thoa sóng âm, các điểm cực đại âm thanh được tạo ra khi hai sóng âm từ hai nguồn dao động gặp nhau và cùng pha tại một vị trí. Cường độ âm thanh tại những điểm này sẽ là lớn nhất. Để xác định vị trí của các điểm cực đại, ta sử dụng công thức:
- Hiệu đường đi của hai sóng đến vị trí cần tính: \[ \Delta d = d_2 - d_1 = k\lambda \] với \(k\) là số nguyên đại diện cho thứ tự của các điểm cực đại (k = 0, ±1, ±2, ...), và \(\lambda\) là bước sóng.
- Khi \(d_2 - d_1 = k\lambda\), vị trí đó sẽ là một điểm cực đại.
Ví dụ: Giả sử hai nguồn âm cách nhau một khoảng \(S_1S_2 = 1.5 \, m\), phát ra sóng âm có bước sóng \(\lambda = 0.5 \, m\). Ta cần tính vị trí các điểm cực đại trên đoạn thẳng nối hai nguồn.
- Từ công thức \(d_2 - d_1 = k\lambda\), ta có các điểm cực đại tại các vị trí:
- Khi \(k = 0\), \(d_2 - d_1 = 0\), tức là điểm giữa của đoạn thẳng \(S_1S_2\).
- Khi \(k = 1\), \(d_2 - d_1 = 0.5 \, m\), tức là điểm cách \(S_1\) một khoảng \(0.75 \, m\).
- Khi \(k = 2\), \(d_2 - d_1 = 1.0 \, m\), tức là điểm cách \(S_1\) một khoảng \(1.25 \, m\).
Như vậy, với bước sóng \(\lambda = 0.5 \, m\), các điểm cực đại âm thanh sẽ xuất hiện ở các vị trí cách đều nhau dọc theo đoạn \(S_1S_2\), mỗi khoảng cách bằng \(\frac{\lambda}{2}\).
Nhận xét: Vị trí của các điểm cực đại phụ thuộc vào hiệu đường đi và bước sóng của hai sóng gặp nhau. Bằng cách điều chỉnh khoảng cách giữa các nguồn hoặc thay đổi bước sóng, ta có thể thay đổi vị trí các điểm cực đại âm thanh.

3. Bài Tập Tính Độ Lệch Pha Trong Giao Thoa Sóng Âm
Trong hiện tượng giao thoa sóng âm, độ lệch pha giữa hai sóng tại một điểm bất kỳ quyết định xem điểm đó sẽ là điểm cực đại hay cực tiểu. Bài tập dưới đây sẽ giúp bạn hiểu rõ cách tính toán độ lệch pha này.
Bài tập:
Hai nguồn âm S1 và S2 cách nhau khoảng cách \( d = 4\;m \), phát ra âm thanh với cùng tần số và biên độ, nhưng có độ lệch pha ban đầu là \( \phi_0 = \frac{\pi}{2} \). Hãy xác định độ lệch pha tại một điểm M nằm trên đường thẳng nối S1 và S2, cách S1 một khoảng \( r_1 = 2\;m \) và cách S2 một khoảng \( r_2 = 3\;m \).
Lời giải:
- Xác định bước sóng \( \lambda \) của sóng âm:
Giả sử tần số sóng là \( f = 500\;Hz \) và vận tốc âm thanh trong không khí là \( v = 340\;m/s \), ta có:
\[
\lambda = \frac{v}{f} = \frac{340}{500} = 0.68\;m
\] - Tính độ lệch pha giữa sóng từ S1 và S2 tại điểm M:
Độ lệch pha do khác biệt khoảng cách là:
\[
\Delta \phi = \frac{2\pi (r_2 - r_1)}{\lambda} = \frac{2\pi (3 - 2)}{0.68} = \frac{2\pi}{0.68} = 9.24\;rad
\] - Cộng thêm độ lệch pha ban đầu \( \phi_0 \):
Tổng độ lệch pha tại điểm M là:
\[
\phi_M = \Delta \phi + \phi_0 = 9.24 + \frac{\pi}{2} = 9.24 + 1.57 = 10.81\;rad
\] - Xác định điểm M là cực đại hay cực tiểu:
Điểm M sẽ là điểm cực đại nếu:
\[
\frac{\phi_M}{2\pi} = k, \;k\in\mathbb{Z}
\]
Với giá trị \( \phi_M = 10.81\), ta thấy điểm M không là điểm cực đại hay cực tiểu hoàn toàn, mà thuộc về vị trí giao thoa trung gian.
4. Bài Tập Xác Định Cường Độ Âm Qua Giao Thoa
Giao thoa sóng âm là hiện tượng hai hay nhiều sóng kết hợp lại với nhau tạo nên các vùng có cường độ âm khác nhau. Các vùng có cường độ âm lớn gọi là cực đại, và các vùng có cường độ âm nhỏ hoặc bằng không gọi là cực tiểu. Để giải quyết bài tập liên quan đến xác định cường độ âm qua giao thoa, chúng ta có thể làm theo các bước chi tiết dưới đây.
Bài toán mẫu
Giả sử có hai nguồn âm kết hợp, phát ra sóng âm với biên độ \( A_1 \) và \( A_2 \). Khoảng cách giữa hai nguồn là \( d \), và khoảng cách đến điểm quan sát là \( r_1 \) và \( r_2 \). Hãy tính cường độ âm tại điểm quan sát.
Phương pháp giải
-
Bước 1: Tính độ lệch pha giữa hai sóng tại điểm quan sát.
Độ lệch pha giữa hai sóng tại điểm quan sát được tính bằng công thức:
\[ \Delta \phi = \frac{2\pi}{\lambda} (r_2 - r_1) \]Trong đó \( \lambda \) là bước sóng, \( r_1 \) và \( r_2 \) lần lượt là khoảng cách từ hai nguồn đến điểm quan sát.
-
Bước 2: Xác định biên độ tổng hợp của sóng tại điểm quan sát.
Biên độ tổng hợp của sóng tại điểm quan sát được tính bằng:
\[ A_{\text{tổng}} = \sqrt{A_1^2 + A_2^2 + 2A_1A_2 \cos(\Delta \phi)} \]Trong đó \( A_1 \) và \( A_2 \) là biên độ của hai sóng, và \( \Delta \phi \) là độ lệch pha.
-
Bước 3: Tính cường độ âm tại điểm quan sát.
Cường độ âm tại điểm quan sát được tính theo công thức:
\[ I = A_{\text{tổng}}^2 \]Trong đó \( A_{\text{tổng}} \) là biên độ tổng hợp của sóng tại điểm quan sát.
Ví dụ cụ thể
Xét hai nguồn âm cách nhau 2 m, phát ra sóng âm có biên độ lần lượt là 3 đơn vị và 4 đơn vị. Điểm quan sát cách nguồn thứ nhất 3 m và cách nguồn thứ hai 5 m. Bước sóng của sóng âm là 1 m. Hãy tính cường độ âm tại điểm quan sát.
-
Bước 1: Tính độ lệch pha:
\[ \Delta \phi = \frac{2\pi}{1}(5 - 3) = 4\pi \]Do \( \cos(4\pi) = 1 \), ta có độ lệch pha là 0.
-
Bước 2: Tính biên độ tổng hợp:
\[ A_{\text{tổng}} = \sqrt{3^2 + 4^2 + 2 \cdot 3 \cdot 4 \cdot \cos(0)} = \sqrt{9 + 16 + 24} = \sqrt{49} = 7 \] -
Bước 3: Tính cường độ âm:
\[ I = 7^2 = 49 \text{ đơn vị cường độ âm.} \]
5. Bài Tập Về Giao Thoa Sóng Âm Qua Hai Nguồn Phát
Trong bài tập này, chúng ta sẽ tìm hiểu cách xác định các vị trí của các điểm giao thoa trong hiện tượng sóng âm phát ra từ hai nguồn. Các bài tập dưới đây sẽ giúp bạn nắm vững cách tính toán và hiểu rõ về hiện tượng giao thoa sóng âm.
Bài Tập 1: Xác Định Vị Trí Các Điểm Cực Đại Âm Thanh
Giả sử hai nguồn sóng âm A và B dao động cùng pha, phát ra âm thanh có bước sóng \(\lambda\) và cách nhau một khoảng \(d\). Hãy xác định vị trí các điểm cực đại âm thanh trên đường nối A và B.
Giải:
- Tính khoảng cách từ một điểm M bất kỳ trên đường nối A và B đến hai nguồn A và B, ký hiệu là \(d_A\) và \(d_B\).
- Điều kiện để M là điểm cực đại: \(d_B - d_A = k\lambda\) với \(k \in \mathbb{Z}\).
- Xác định giá trị của \(k\) để tìm ra các vị trí của điểm M.
Bài Tập 2: Tính Khoảng Cách Giữa Các Vùng Âm Yếu
Hai nguồn sóng âm cách nhau một khoảng \(d\) và phát ra âm thanh cùng tần số, cùng pha. Hãy tính khoảng cách giữa hai vùng âm yếu gần nhất trên đường nối A và B.
Giải:
- Điều kiện để M là điểm âm yếu: \(d_B - d_A = (k + \frac{1}{2})\lambda\) với \(k \in \mathbb{Z}\).
- Khoảng cách giữa hai vùng âm yếu gần nhất: \(\Delta x = \frac{\lambda}{2}\).
Bài Tập 3: Xác Định Sự Triệt Tiêu Của Sóng Âm
Hai nguồn âm cách nhau một khoảng \(d\), dao động cùng pha, phát ra sóng âm có bước sóng \(\lambda\). Xác định vị trí các điểm mà tại đó sự triệt tiêu hoàn toàn xảy ra.
Giải:
- Điều kiện để xảy ra triệt tiêu: \(d_B - d_A = (2k + 1)\frac{\lambda}{2}\) với \(k \in \mathbb{Z}\).
- Tính khoảng cách giữa các điểm triệt tiêu liên tiếp trên đường nối hai nguồn.
Bài Tập 4: Tính Tần Số Cộng Hưởng Trong Giao Thoa Sóng Âm
Giả sử hai nguồn âm A và B dao động cùng pha với nhau. Khoảng cách giữa chúng là \(d\), tần số sóng âm là \(f\), vận tốc âm trong không khí là \(v\). Tính tần số cộng hưởng của hệ thống.
Giải:
- Đầu tiên, xác định bước sóng \(\lambda = \frac{v}{f}\).
- Điều kiện cộng hưởng xảy ra khi khoảng cách giữa hai nguồn bằng một số nguyên lần của bước sóng: \(d = n\lambda\) với \(n \in \mathbb{Z}\).
- Tính tần số cộng hưởng: \(f = \frac{nv}{d}\).
6. Bài Tập Tính Khoảng Cách Giữa Các Vùng Âm Yếu
Trong hiện tượng giao thoa sóng, các vùng âm yếu (cực tiểu) xuất hiện tại các điểm mà hai sóng gặp nhau và triệt tiêu lẫn nhau. Để tính khoảng cách giữa các vùng âm yếu, chúng ta cần dựa vào điều kiện giao thoa của hai sóng từ hai nguồn kết hợp cùng pha hoặc ngược pha.
Với hai nguồn cùng pha, khoảng cách giữa hai vùng âm yếu liên tiếp được xác định bởi công thức:
Nếu hai nguồn dao động ngược pha, khoảng cách giữa hai vùng âm yếu sẽ là:
Dưới đây là ví dụ minh họa:
- Giả sử hai nguồn phát sóng cùng pha \( S_1 \) và \( S_2 \) cách nhau một khoảng \( l = 5\;m \) và bước sóng \( \lambda = 1\;m \).
- Các vùng âm yếu sẽ xuất hiện tại các vị trí có hiệu đường đi từ hai nguồn đến đó bằng \( (k + 0.5) \lambda \), với \( k \) là số nguyên.
Do đó, khoảng cách giữa hai vùng âm yếu liên tiếp là:
Vì vậy, giữa hai vùng âm yếu, khoảng cách nhỏ nhất chính là 0.5 m.
Các bước thực hiện để tính toán:
- Xác định bước sóng \( \lambda \) của sóng.
- Xác định điều kiện giao thoa (cùng pha hoặc ngược pha).
- Sử dụng công thức tương ứng để tính khoảng cách giữa các vùng âm yếu.
- Thay các giá trị cụ thể vào công thức để tính toán kết quả.
7. Bài Tập Xác Định Sự Triệt Tiêu Của Sóng Âm
Trong hiện tượng giao thoa sóng, sự triệt tiêu của sóng âm xảy ra khi hai sóng gặp nhau và có biên độ đối lập. Điều này dẫn đến các điểm dao động với biên độ bằng 0, được gọi là các điểm nút hoặc vùng triệt tiêu.
Để xác định sự triệt tiêu của sóng âm tại một điểm, ta cần xét hai yếu tố chính: độ lệch pha giữa hai sóng và khoảng cách từ điểm đó đến các nguồn sóng. Các bài tập dưới đây sẽ giúp bạn hiểu rõ hơn về cách xác định những vị trí này.
- Bước 1: Xác định phương trình sóng tại hai nguồn kết hợp \( S_1 \) và \( S_2 \).
- Bước 2: Tính toán khoảng cách từ điểm cần xác định đến hai nguồn, kí hiệu là \( d_1 \) và \( d_2 \).
- Bước 3: Kiểm tra điều kiện triệt tiêu của sóng, điều này xảy ra khi hiệu số đường đi bằng một số nguyên lần của bước sóng: \[ d_2 - d_1 = \left( k + \frac{1}{2} \right) \lambda \] với \( k \) là số nguyên.
- Bước 4: Xác định các vị trí trên trục tọa độ thoả mãn điều kiện trên để tìm các điểm nút.
Ví dụ: Xét hai nguồn âm phát ra sóng với tần số \( f = 500 \, \text{Hz} \) và tốc độ âm thanh trong không khí là \( v = 340 \, \text{m/s} \). Bước sóng của sóng âm được tính là:
Nếu khoảng cách giữa hai nguồn là \( d = 2 \, \text{m} \), khoảng cách từ điểm cần xác định đến hai nguồn lần lượt là \( d_1 = 1.5 \, \text{m} \) và \( d_2 = 0.5 \, \text{m} \), ta có:
Kiểm tra điều kiện triệt tiêu:
Giải phương trình trên để tìm các giá trị của \( k \) thỏa mãn điều kiện triệt tiêu và xác định các vị trí tương ứng.
Bằng cách này, bạn có thể xác định chính xác các điểm có sự triệt tiêu của sóng âm trong một không gian giao thoa sóng.
8. Bài Tập Về Giao Thoa Sóng Âm Trong Không Khí
Dưới đây là một bài tập về giao thoa sóng âm trong không khí, giúp bạn hiểu rõ hơn về hiện tượng này và cách tính toán liên quan.
Bài tập: Hai nguồn âm S1 và S2 cùng phát ra sóng âm với tần số 1000 Hz và dao động đồng pha. Khoảng cách giữa hai nguồn là 2 m. Vận tốc truyền âm trong không khí là 340 m/s. Hãy xác định vị trí của các điểm giao thoa cực đại và cực tiểu trên đường thẳng nối hai nguồn.
Giải:
- Tính bước sóng của sóng âm:
\[ \lambda = \frac{v}{f} = \frac{340 \, \text{m/s}}{1000 \, \text{Hz}} = 0,34 \, \text{m} \] - Xác định vị trí các điểm giao thoa cực đại (cộng hưởng):
Điều kiện để xảy ra giao thoa cực đại là:
\[ \Delta d = k\lambda \quad \text{với} \ k \in \mathbb{Z} \] Trong đó, \( \Delta d \) là hiệu đường đi từ hai nguồn đến điểm cần xác định. - Xác định vị trí các điểm giao thoa cực tiểu (triệt tiêu):
Điều kiện để xảy ra giao thoa cực tiểu là:
\[ \Delta d = \left(k + \frac{1}{2}\right)\lambda \quad \text{với} \ k \in \mathbb{Z} \] - Tính toán cụ thể các vị trí:
- Điểm cực đại: \( k = 0, 1, 2, \ldots \)
- Điểm cực tiểu: \( k = 0, 1, 2, \ldots \)
Qua bài tập này, bạn có thể thấy rằng việc xác định các điểm cực đại và cực tiểu trên đường nối hai nguồn giúp hiểu rõ hơn về sự giao thoa sóng âm trong không khí. Đây là hiện tượng quan trọng trong nhiều ứng dụng thực tế như thiết kế hệ thống âm thanh, nghiên cứu sóng âm, và xử lý tín hiệu âm thanh.

9. Bài Tập Xác Định Khoảng Cách Giữa Các Nút Sóng Âm
Trong hiện tượng giao thoa sóng âm, khoảng cách giữa các nút sóng được xác định dựa trên bước sóng \( \lambda \) và các yếu tố liên quan đến hai nguồn phát sóng kết hợp. Các nút sóng là các vị trí mà tại đó biên độ dao động bằng 0 do sự triệt tiêu lẫn nhau của hai sóng kết hợp.
Để xác định khoảng cách giữa các nút sóng, chúng ta cần xem xét công thức sau:
Vị trí của nút sóng được xác định khi hiệu đường đi giữa hai sóng đến điểm đó là một bội số lẻ của nửa bước sóng:
\[ d_2 - d_1 = (k + 0.5) \cdot \lambda \] với \( k = 0, 1, 2, 3, \dots \)Khoảng cách giữa hai nút sóng liền kề chính là một nửa bước sóng:
\[ \Delta d = \frac{\lambda}{2} \]
Ví dụ: Cho hai nguồn âm \( S_1 \) và \( S_2 \) dao động cùng pha, cách nhau một khoảng \( d \). Bước sóng của âm là \( \lambda \). Xác định khoảng cách giữa hai nút sóng gần nhau nhất.
- Áp dụng công thức xác định khoảng cách giữa hai nút sóng liền kề:
-
Vị trí của các nút sóng được xác định bởi hiệu đường đi \( d_2 - d_1 = (k + 0.5) \cdot \lambda \), với \( k \) là số nguyên dương.
Khoảng cách giữa hai nút sóng gần nhau nhất là:
\[ \Delta d = \frac{\lambda}{2} \] - Do đó, khoảng cách giữa hai nút sóng gần nhau nhất là \( \frac{\lambda}{2} \).
Việc tính toán chính xác các vị trí nút sóng rất quan trọng trong các bài toán liên quan đến âm học và các ứng dụng trong thực tiễn như thiết kế phòng thu âm, hệ thống âm thanh vòm, v.v.
10. Bài Tập Tính Số Lần Cộng Hưởng Trong Một Chu Kỳ
Để tính số lần cộng hưởng trong một chu kỳ giao thoa sóng, ta cần xác định điều kiện để xảy ra cộng hưởng và tính toán số lần thỏa mãn điều kiện đó trong khoảng thời gian một chu kỳ.
Bước 1: Xác định điều kiện cộng hưởng.
- Điều kiện để xảy ra cộng hưởng là hiệu đường đi của hai sóng tại một điểm phải bằng một số nguyên lần của bước sóng: \( \Delta d = k\lambda \) với \( k \) là số nguyên.
Bước 2: Thiết lập phương trình cho giao thoa sóng.
- Giả sử hai nguồn sóng \( S_1 \) và \( S_2 \) dao động cùng pha và phát ra sóng với cùng tần số \( f \) và bước sóng \( \lambda \).
- Điểm M là điểm khảo sát, cách \( S_1 \) một khoảng \( d_1 \) và cách \( S_2 \) một khoảng \( d_2 \). Khi đó, hiệu đường đi \( \Delta d = |d_1 - d_2| \).
- Phương trình giao thoa tại M có dạng:
\[ u_M = 2A \cos \left( \frac{\pi \Delta d}{\lambda} \right) \cos \left( \omega t - \frac{2\pi d_1}{\lambda} \right) \]
Bước 3: Tính số lần cộng hưởng trong một chu kỳ.
- Trong một chu kỳ \( T \), để điểm M cộng hưởng, \( \cos \left( \frac{\pi \Delta d}{\lambda} \right) \) phải đạt giá trị cực đại.
- Điều kiện này xảy ra khi \( \frac{\Delta d}{\lambda} = k \) với \( k \) là số nguyên.
- Vì \( k \) có thể nhận nhiều giá trị nguyên khác nhau trong một chu kỳ, số lần cộng hưởng chính là số giá trị của \( k \) thỏa mãn.
Ví dụ:
- Giả sử \( d_1 = 3 \)m, \( d_2 = 2 \)m, và \( \lambda = 1 \)m. Tính số lần cộng hưởng trong một chu kỳ.
- Hiệu đường đi: \( \Delta d = |3 - 2| = 1 \)m.
- Áp dụng điều kiện cộng hưởng: \( \Delta d = k\lambda \Rightarrow k = 1 \).
- Do \( k \) chỉ nhận một giá trị nguyên trong trường hợp này, nên chỉ có 1 lần cộng hưởng trong một chu kỳ.