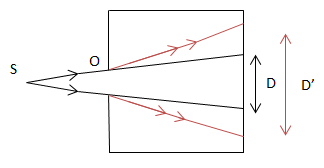
Trong Thí Nghiệm Giao Thoa Ánh Sáng Khoảng Vân Sẽ: Cách Tính Và Ứng Dụng Thực Tiễn

Trong thí nghiệm giao thoa ánh sáng, khoảng vân là khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp trên màn quan sát. Đây là một yếu tố quan trọng trong việc xác định tính chất sóng của ánh sáng. Khoảng vân được tính theo công thức:

\[ i = \dfrac{\lambda D}{a} \]

• \(\lambda\): Bước sóng của ánh sáng (đơn vị: mét)
• D: Khoảng cách từ hai khe đến màn quan sát (đơn vị: mét)
• a: Khoảng cách giữa hai khe (đơn vị: mét)

Ứng Dụng Thực Tế

Thí nghiệm này thường được ứng dụng để đo bước sóng của các loại ánh sáng khác nhau. Bằng cách điều chỉnh khoảng cách giữa các khe và khoảng cách từ khe đến màn, ta có thể quan sát sự thay đổi của khoảng vân và từ đó suy ra các tính chất của nguồn sáng.

Ví Dụ Cụ Thể

Giả sử trong một thí nghiệm, ánh sáng có bước sóng \(\lambda = 600 \, \text{nm}\), khoảng cách từ hai khe đến màn là \(D = 1 \, \text{m}\) và khoảng cách giữa hai khe là \(a = 0.5 \, \text{mm}\). Khi đó, khoảng vân sẽ được tính như sau:

\[ i = \dfrac{600 \times 10^{-9} \times 1}{0.5 \times 10^{-3}} = 1.2 \times 10^{-3} \, \text{m} = 1.2 \, \text{mm} \]

Điều này có nghĩa là các vân sáng và vân tối sẽ xuất hiện cách nhau 1.2 mm trên màn quan sát.

Kết Luận

Khoảng vân trong thí nghiệm giao thoa ánh sáng cung cấp những thông tin quan trọng về bước sóng của ánh sáng và đặc điểm sóng của ánh sáng. Việc nắm vững công thức tính khoảng vân giúp chúng ta hiểu sâu hơn về tính chất của ánh sáng và các ứng dụng thực tế trong khoa học và kỹ thuật.

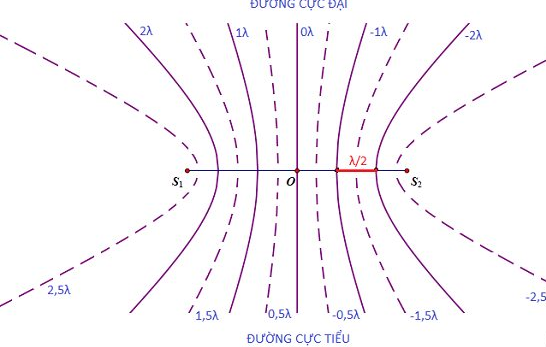
Giao thoa ánh sáng là một hiện tượng quan trọng trong vật lý, minh chứng cho tính chất sóng của ánh sáng. Hiện tượng này xảy ra khi hai hay nhiều chùm sáng gặp nhau và chồng chập lên nhau, tạo ra các vùng sáng và tối xen kẽ nhau gọi là các vân giao thoa.

1.1. Hiện Tượng Giao Thoa Ánh Sáng

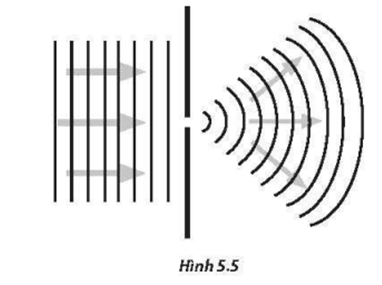
Hiện tượng giao thoa ánh sáng có thể quan sát được rõ ràng nhất trong thí nghiệm của Thomas Young. Trong thí nghiệm này, ánh sáng được chiếu qua hai khe hẹp song song, cách nhau một khoảng nhỏ. Sau khi đi qua các khe, hai chùm sáng giao thoa với nhau trên màn quan sát, tạo ra các vân sáng và tối. Các vân sáng tương ứng với các điểm mà hai sóng ánh sáng gặp nhau đồng pha, còn các vân tối xuất hiện khi hai sóng gặp nhau ngược pha.

1.2. Điều Kiện Để Xảy Ra Giao Thoa Ánh Sáng

• Hai nguồn sáng phải là các nguồn kết hợp, nghĩa là chúng phải phát ra ánh sáng có cùng tần số và có mối tương quan pha cố định.
• Ánh sáng từ hai nguồn phải có sự chồng chập lên nhau trong không gian.
• Thí nghiệm phải được thực hiện trong môi trường ổn định, không có sự nhiễu loạn.

Thí nghiệm giao thoa ánh sáng không chỉ chứng minh tính chất sóng của ánh sáng mà còn có nhiều ứng dụng quan trọng trong đo lường và công nghệ quang học, từ việc xác định bước sóng của ánh sáng đến các ứng dụng trong công nghệ laser và đo lường chính xác.

2.1. Định Nghĩa Khoảng Vân

Trong thí nghiệm giao thoa ánh sáng, khoảng vân là khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp trên màn quan sát. Khoảng vân được ký hiệu là \(i\) và đóng vai trò quan trọng trong việc xác định các đặc điểm của hiện tượng giao thoa.

2.2. Công Thức Tính Khoảng Vân

Công thức tính khoảng vân trong thí nghiệm giao thoa ánh sáng được xác định như sau:

Trong đó:

• \(\lambda\): Bước sóng của ánh sáng (đơn vị: mét).
• \(D\): Khoảng cách từ các khe sáng đến màn quan sát (đơn vị: mét).
• \(a\): Khoảng cách giữa hai khe sáng (đơn vị: mét).

2.3. Ảnh Hưởng Của Khoảng Cách Giữa Các Khe Đến Khoảng Vân

Khoảng vân \(i\) tỷ lệ nghịch với khoảng cách giữa hai khe sáng \(a\). Khi \(a\) tăng lên, khoảng vân \(i\) sẽ giảm và ngược lại. Điều này có nghĩa là các vân sáng và vân tối trên màn sẽ càng gần nhau hơn khi khoảng cách giữa các khe tăng lên.

2.4. Ứng Dụng Của Khoảng Vân Trong Đo Lường

Khoảng vân trong thí nghiệm giao thoa ánh sáng không chỉ giúp xác định tính chất của sóng ánh sáng mà còn được ứng dụng trong việc đo lường bước sóng ánh sáng. Bằng cách biết khoảng cách giữa các khe và khoảng cách từ khe đến màn, người ta có thể xác định chính xác bước sóng của ánh sáng.

Hiện tượng giao thoa ánh sáng là một minh chứng rõ ràng cho bản chất sóng của ánh sáng. Trong thí nghiệm giao thoa ánh sáng, khoảng vân là một yếu tố quan trọng để xác định vị trí các vân sáng và vân tối. Tuy nhiên, hiện tượng này bị ảnh hưởng bởi nhiều yếu tố khác nhau.

• Bước sóng ánh sáng (\(\lambda\)): Bước sóng của ánh sáng càng lớn thì khoảng vân càng lớn. Điều này có nghĩa là khi sử dụng các nguồn sáng đơn sắc với bước sóng khác nhau, khoảng cách giữa các vân sáng và vân tối trên màn cũng sẽ khác nhau. Công thức xác định khoảng vân là: \[ i = \frac{\lambda D}{a} \] Trong đó, \(D\) là khoảng cách từ nguồn sáng đến màn, \(a\) là khoảng cách giữa hai khe.
• Khoảng cách giữa hai khe (a): Khi khoảng cách giữa hai khe tăng, khoảng vân giảm, nghĩa là các vân sáng và vân tối sẽ gần nhau hơn. Ngược lại, nếu khoảng cách này giảm, các vân sẽ thưa hơn.
• Khoảng cách từ màn đến hai khe (D): Khi tăng khoảng cách từ màn đến hai khe, khoảng vân cũng tăng lên. Điều này là do sự phân tán của các tia sáng khi di chuyển trên khoảng cách lớn hơn, dẫn đến sự tách biệt rõ ràng hơn giữa các vân.
• Điều kiện quan sát: Độ chính xác của thí nghiệm giao thoa ánh sáng còn phụ thuộc vào các yếu tố như độ ổn định của nguồn sáng, độ chính xác trong việc đặt các khe, và các yếu tố môi trường như nhiệt độ và áp suất. Nhiễu loạn từ môi trường có thể làm sai lệch kết quả thí nghiệm.

Những yếu tố trên cần được kiểm soát chặt chẽ trong quá trình thực hiện thí nghiệm để đảm bảo độ chính xác và tính lặp lại của các kết quả quan sát.

Thí nghiệm giao thoa ánh sáng không chỉ là một công cụ quan trọng trong vật lý lý thuyết mà còn có nhiều ứng dụng thực tiễn trong đời sống và công nghệ hiện đại. Dưới đây là một số ứng dụng nổi bật:

• Kiểm tra chất lượng bề mặt: Thí nghiệm giao thoa ánh sáng được sử dụng trong công nghệ quang học để kiểm tra độ phẳng và chất lượng bề mặt của các vật liệu. Khi ánh sáng được chiếu qua bề mặt, các vân giao thoa sẽ xuất hiện, và sự sai lệch của các vân này có thể cho biết sự không đồng đều trên bề mặt.
• Đo lường bước sóng ánh sáng: Một trong những ứng dụng quan trọng của thí nghiệm này là đo lường chính xác bước sóng của ánh sáng. Bằng cách điều chỉnh khoảng cách giữa các khe hoặc khoảng cách từ khe đến màn, ta có thể xác định bước sóng của các nguồn sáng đơn sắc khác nhau.
• Ứng dụng trong viễn thông: Trong công nghệ viễn thông, thí nghiệm giao thoa ánh sáng đóng vai trò quan trọng trong việc phát triển các thiết bị truyền dẫn quang học. Sự giao thoa ánh sáng được sử dụng để kiểm soát và điều chỉnh bước sóng của tín hiệu quang học, từ đó cải thiện hiệu suất truyền dẫn.
• Ứng dụng trong đo lường khoảng cách: Thí nghiệm giao thoa ánh sáng cũng được áp dụng trong các thiết bị đo lường khoảng cách chính xác, chẳng hạn như các máy đo khoảng cách laser. Sự giao thoa của ánh sáng phản xạ từ các bề mặt khác nhau giúp xác định khoảng cách với độ chính xác cao.

Nhờ vào những ứng dụng này, thí nghiệm giao thoa ánh sáng đã trở thành một công cụ không thể thiếu trong nhiều lĩnh vực khoa học và công nghệ, từ nghiên cứu cơ bản đến phát triển các thiết bị công nghệ cao.

Dưới đây là một số bài tập về hiện tượng giao thoa ánh sáng, kèm theo lời giải chi tiết để bạn có thể nắm vững kiến thức và áp dụng vào thực tế.

• Bài tập 1: Tính khoảng vân \(i\) trong thí nghiệm giao thoa ánh sáng với các thông số sau: khoảng cách giữa hai khe \(a = 0,5 \, mm\), khoảng cách từ hai khe đến màn \(D = 1,5 \, m\), bước sóng của ánh sáng sử dụng \(\lambda = 600 \, nm\).

Lời giải:

1. Sử dụng công thức tính khoảng vân \(i\): \[ i = \frac{\lambda \cdot D}{a} \]
2. Thay các giá trị đã cho vào công thức: \[ i = \frac{600 \times 10^{-9} \cdot 1,5}{0,5 \times 10^{-3}} = 1,8 \, mm \]
• Bài tập 2: Tính vị trí vân sáng thứ 3 trên màn quan sát khi biết khoảng cách từ khe đến màn \(D = 2 \, m\), khoảng cách giữa hai khe \(a = 0,25 \, mm\), và bước sóng ánh sáng là \( \lambda = 500 \, nm\).

Lời giải:

1. Vị trí vân sáng thứ \(k\) được tính theo công thức: \[ x_s = k \cdot \frac{\lambda \cdot D}{a} \]
2. Với \(k = 3\), thay số vào ta được: \[ x_s = 3 \cdot \frac{500 \times 10^{-9} \cdot 2}{0,25 \times 10^{-3}} = 12 \, mm \]
• Bài tập 3: Trong thí nghiệm Y-âng, nếu tăng khoảng cách giữa hai khe lên gấp đôi, khoảng vân \(i\) sẽ thay đổi như thế nào?

Lời giải:

1. Khi tăng khoảng cách giữa hai khe lên gấp đôi, tức là \(a' = 2a\), thì khoảng vân mới \(i'\) sẽ là: \[ i' = \frac{\lambda \cdot D}{a'} = \frac{\lambda \cdot D}{2a} = \frac{i}{2} \]
2. Vậy khoảng vân sẽ giảm đi một nửa so với ban đầu.

Những bài tập trên giúp củng cố kiến thức về hiện tượng giao thoa ánh sáng và các ứng dụng của nó trong việc đo lường và phân tích các đặc tính của ánh sáng.

Trong thí nghiệm giao thoa ánh sáng, khoảng vân là một đại lượng quan trọng, phản ánh sự tương tác giữa các sóng ánh sáng. Khoảng vân phụ thuộc vào nhiều yếu tố như bước sóng của ánh sáng, khoảng cách giữa các khe và khoảng cách từ các khe đến màn quan sát. Qua quá trình phân tích, ta có thể rút ra một số kết luận quan trọng sau:

• Khoảng vân và bước sóng: Khoảng vân \(\Delta x\) tỉ lệ thuận với bước sóng của ánh sáng \(\lambda\). Khi bước sóng tăng, khoảng vân cũng tăng, giúp ta có thể quan sát rõ hơn các vân sáng và vân tối trên màn.
• Khoảng vân và khoảng cách giữa các khe: Khoảng vân \(\Delta x\) tỉ lệ nghịch với khoảng cách giữa hai khe \(a\). Nếu khoảng cách giữa hai khe tăng, khoảng vân sẽ giảm và ngược lại. Điều này cho phép ta điều chỉnh thí nghiệm để thu được kết quả mong muốn.
• Khoảng vân và khoảng cách từ khe đến màn: Khoảng vân \(\Delta x\) cũng tỉ lệ thuận với khoảng cách từ các khe đến màn quan sát \(D\). Khi tăng khoảng cách này, các vân sáng và tối sẽ trở nên rõ ràng hơn.

Kết quả thí nghiệm không chỉ giúp khẳng định lý thuyết về hiện tượng giao thoa ánh sáng mà còn cung cấp những ứng dụng thực tiễn trong nhiều lĩnh vực, từ quang học đến các công nghệ hiện đại. Việc hiểu rõ các yếu tố ảnh hưởng đến khoảng vân sẽ giúp chúng ta thiết kế các thí nghiệm và ứng dụng quang học một cách hiệu quả hơn.