Chủ đề trong thí nghiệm giao thoa sóng ở mặt nước: Trong thí nghiệm giao thoa sóng ở mặt nước, bạn sẽ khám phá cách thực hiện thí nghiệm này một cách chi tiết và chính xác. Bài viết cung cấp hướng dẫn từng bước, phân tích kết quả, và các ứng dụng thực tế của hiện tượng giao thoa sóng trong đời sống và nghiên cứu khoa học.
Mục lục
- Thí Nghiệm Giao Thoa Sóng Ở Mặt Nước
- Giới Thiệu Về Thí Nghiệm Giao Thoa Sóng Ở Mặt Nước
- Quy Trình Thực Hiện Thí Nghiệm Giao Thoa Sóng
- Phân Tích Và Tính Toán Kết Quả Thí Nghiệm
- Ứng Dụng Thực Tế Của Thí Nghiệm Giao Thoa Sóng
- 10 Dạng Bài Tập Về Giao Thoa Sóng Ở Mặt Nước
- Dạng 1: Tính Bước Sóng Dựa Trên Khoảng Cách Giữa Các Vân Giao Thoa
- Dạng 2: Xác Định Số Điểm Cực Đại Trên Đoạn Thẳng Giữa Hai Nguồn
- Dạng 3: Tính Tốc Độ Truyền Sóng Dựa Trên Các Thông Số Đã Cho
- Dạng 4: Xác Định Khoảng Cách Giữa Hai Nguồn Sóng
- Dạng 5: Phân Tích Tác Động Của Tần Số Sóng Đến Hiện Tượng Giao Thoa
- Dạng 6: Xác Định Khoảng Cách Giữa Hai Vân Liên Tiếp
- Dạng 7: Tính Toán Biên Độ Của Sóng Tại Các Vị Trí Khác Nhau
- Dạng 8: Phân Tích Ảnh Hưởng Của Biên Độ Dao Động Đến Hiện Tượng Giao Thoa
- Dạng 9: Tính Số Vân Giao Thoa Trên Một Đoạn Xác Định
- Dạng 10: So Sánh Kết Quả Thực Nghiệm Với Lý Thuyết
Thí Nghiệm Giao Thoa Sóng Ở Mặt Nước
Thí nghiệm giao thoa sóng trên mặt nước là một thí nghiệm cơ bản trong vật lý học để nghiên cứu hiện tượng giao thoa, một trong những tính chất quan trọng của sóng. Thí nghiệm này giúp quan sát và hiểu cách các sóng từ hai nguồn tương tác với nhau, tạo ra các vân giao thoa đặc trưng trên mặt nước.
Chuẩn Bị Thí Nghiệm
- Một bể nước nông và rộng.
- Hai nguồn phát sóng đồng pha (có thể sử dụng hai quả bóng nhỏ hoặc hai thanh kim loại).
- Thiết bị tạo dao động (máy phát sóng hoặc thiết bị gõ).
- Thước đo và bút chì.
- Máy quay hoặc máy chụp ảnh để ghi lại kết quả.
- Nguồn sáng mạnh như đèn laser để chiếu sáng bề mặt nước.
Quy Trình Thực Hiện Thí Nghiệm
- Đổ nước vào bể sao cho độ sâu vừa đủ để tạo sóng rõ ràng trên mặt nước.
- Đặt hai nguồn dao động tại hai điểm cố định trên mặt nước, cách nhau một khoảng xác định.
- Kích hoạt hai nguồn sóng đồng pha để tạo ra các sóng truyền trên mặt nước.
- Quan sát các vân giao thoa xuất hiện trên mặt nước khi hai sóng gặp nhau.
- Ghi lại hình dạng và vị trí của các vân giao thoa bằng máy quay hoặc máy chụp ảnh.
Phân Tích Kết Quả
Sau khi hoàn thành thí nghiệm, bạn có thể tiến hành phân tích kết quả bằng cách thực hiện các bước sau:
- Xác định khoảng cách giữa các vân giao thoa, tức là khoảng cách giữa các điểm cực đại và cực tiểu trên mặt nước.
- Tính toán bước sóng của sóng dựa trên khoảng cách giữa các vân giao thoa và khoảng cách giữa hai nguồn sóng.
- So sánh kết quả thực nghiệm với lý thuyết để đánh giá độ chính xác của thí nghiệm.
Công Thức Liên Quan
Trong thí nghiệm này, công thức liên quan đến khoảng cách giữa các vân giao thoa là:
Trong đó:
- \(\Delta x\) là khoảng cách giữa hai vân giao thoa liên tiếp.
- \(\lambda\) là bước sóng của sóng trên mặt nước.
- D là khoảng cách từ nguồn phát sóng đến màn quan sát.
- d là khoảng cách giữa hai nguồn sóng.
Kết Luận
Thí nghiệm giao thoa sóng ở mặt nước là một phương pháp hiệu quả để nghiên cứu các tính chất cơ bản của sóng, đặc biệt là hiện tượng giao thoa. Qua việc phân tích kết quả thí nghiệm, ta có thể hiểu rõ hơn về sự tương tác của các sóng và các yếu tố ảnh hưởng đến sự hình thành vân giao thoa.
.png)
Giới Thiệu Về Thí Nghiệm Giao Thoa Sóng Ở Mặt Nước
Thí nghiệm giao thoa sóng ở mặt nước là một trong những thí nghiệm cơ bản trong vật lý, giúp hiểu rõ hơn về hiện tượng giao thoa - một đặc tính quan trọng của sóng. Hiện tượng này xảy ra khi hai hay nhiều sóng gặp nhau, tạo ra các điểm cực đại và cực tiểu trên mặt nước. Các điểm này tạo thành những vân giao thoa đặc trưng.
Trong thí nghiệm, hai nguồn sóng đồng pha được đặt tại hai điểm cố định trên mặt nước. Khi sóng từ hai nguồn này lan truyền và gặp nhau, chúng sẽ giao thoa, tạo ra các vân giao thoa mà ta có thể quan sát được. Khoảng cách giữa các vân này phụ thuộc vào bước sóng của sóng, khoảng cách giữa hai nguồn, và các yếu tố khác.
Thí nghiệm này không chỉ giúp học sinh và sinh viên nắm bắt được khái niệm giao thoa sóng mà còn ứng dụng trong nhiều lĩnh vực khác như đo lường, kiểm tra vật liệu và nghiên cứu khoa học.
Công thức quan trọng trong thí nghiệm giao thoa sóng ở mặt nước là:
- \(\Delta x\): Khoảng cách giữa hai vân giao thoa liên tiếp.
- \(\lambda\): Bước sóng của sóng trên mặt nước.
- D: Khoảng cách từ nguồn phát sóng đến màn quan sát.
- d: Khoảng cách giữa hai nguồn sóng.
Thí nghiệm giao thoa sóng ở mặt nước không chỉ mang tính chất học thuật mà còn có giá trị thực tiễn cao, giúp chúng ta hiểu rõ hơn về các hiện tượng sóng trong tự nhiên và ứng dụng trong đời sống.
Quy Trình Thực Hiện Thí Nghiệm Giao Thoa Sóng
Để thực hiện thí nghiệm giao thoa sóng ở mặt nước một cách chính xác và hiệu quả, bạn cần tuân thủ các bước sau:
- Chuẩn Bị Thiết Bị: Đặt hai nguồn phát sóng đồng pha tại hai vị trí cố định trên bể nước. Kiểm tra lại các thiết bị để đảm bảo chúng hoạt động đúng chức năng.
- Tạo Dao Động: Sử dụng máy phát dao động hoặc thiết bị gõ để tạo dao động liên tục và đồng đều trên mặt nước. Đảm bảo các dao động từ hai nguồn sóng được phát ra cùng lúc và có tần số giống nhau.
- Quan Sát Hiện Tượng Giao Thoa: Khi hai sóng gặp nhau, chúng sẽ tạo ra các vân giao thoa trên mặt nước. Quan sát các vân giao thoa này, chú ý đến các điểm cực đại và cực tiểu, nơi biên độ sóng lớn nhất hoặc nhỏ nhất.
- Ghi Lại Kết Quả: Sử dụng máy quay hoặc máy ảnh để ghi lại hình ảnh các vân giao thoa. Điều này sẽ giúp bạn phân tích các kết quả sau khi thí nghiệm kết thúc.
- Đo Lường: Dùng thước đo để đo khoảng cách giữa các vân giao thoa liên tiếp (\(\Delta x\)). Sử dụng công thức: \[ \Delta x = \frac{\lambda D}{d} \]
- \(\Delta x\) là khoảng cách giữa hai vân giao thoa liên tiếp.
- \(\lambda\) là bước sóng của sóng.
- D là khoảng cách từ nguồn phát sóng đến màn quan sát.
- d là khoảng cách giữa hai nguồn sóng.
- Phân Tích Kết Quả: So sánh kết quả đo lường với các giá trị lý thuyết, từ đó rút ra kết luận về hiện tượng giao thoa và các yếu tố ảnh hưởng đến nó.
trong đó:
Thí nghiệm giao thoa sóng ở mặt nước giúp bạn hiểu rõ hơn về tính chất của sóng và các hiện tượng giao thoa, đồng thời có thể áp dụng những kiến thức này vào các lĩnh vực thực tiễn.

Phân Tích Và Tính Toán Kết Quả Thí Nghiệm
Sau khi hoàn tất thí nghiệm giao thoa sóng ở mặt nước, việc phân tích và tính toán kết quả là bước quan trọng để hiểu rõ hơn về hiện tượng giao thoa. Dưới đây là các bước chi tiết để phân tích và tính toán kết quả thí nghiệm:
- Quan Sát Các Vân Giao Thoa: Ghi lại hình ảnh các vân giao thoa trên mặt nước bằng cách sử dụng máy quay hoặc máy ảnh. Chú ý đến các điểm cực đại và cực tiểu trên vân, nơi biên độ sóng lớn nhất hoặc nhỏ nhất.
- Đo Lường Khoảng Cách Giữa Các Vân: Sử dụng thước đo để đo khoảng cách giữa hai vân cực đại liên tiếp hoặc hai vân cực tiểu liên tiếp (\(\Delta x\)). Đây là khoảng cách quan trọng để tính toán bước sóng của sóng.
- Tính Toán Bước Sóng: Sử dụng công thức: \[ \lambda = \frac{\Delta x \cdot d}{D} \]
- \(\lambda\): Bước sóng của sóng.
- \(\Delta x\): Khoảng cách giữa hai vân giao thoa liên tiếp.
- d: Khoảng cách giữa hai nguồn phát sóng.
- D: Khoảng cách từ nguồn phát sóng đến màn quan sát.
- So Sánh Với Giá Trị Lý Thuyết: Sau khi tính toán được bước sóng, so sánh giá trị này với các giá trị lý thuyết hoặc giá trị đã biết để xác định độ chính xác của thí nghiệm.
- Phân Tích Sai Số: Xác định các yếu tố có thể gây ra sai số trong thí nghiệm, như độ chính xác của thước đo, sự rung động của bể nước, hoặc sự không đồng pha của các nguồn phát sóng. Từ đó, đưa ra các biện pháp cải thiện cho các thí nghiệm tương lai.
trong đó:
Kết quả thí nghiệm sau khi được phân tích và tính toán sẽ cung cấp cho bạn cái nhìn sâu sắc về hiện tượng giao thoa sóng, cũng như khả năng áp dụng các kiến thức này vào các bài toán và tình huống thực tế.

XEM THÊM:
Ứng Dụng Thực Tế Của Thí Nghiệm Giao Thoa Sóng
Thí nghiệm giao thoa sóng không chỉ là một phần quan trọng trong việc hiểu về các hiện tượng sóng, mà còn có nhiều ứng dụng thực tế đáng chú ý trong nhiều lĩnh vực khác nhau:
- Thiết Kế Hệ Thống Sóng Âm: Nguyên lý giao thoa sóng được ứng dụng trong việc thiết kế hệ thống âm thanh, bao gồm loa và micro, để tối ưu hóa chất lượng âm thanh. Bằng cách điều chỉnh pha và vị trí các nguồn phát, các kỹ sư có thể giảm thiểu các vùng giao thoa tiêu cực và tăng cường chất lượng âm thanh trong không gian.
- Kỹ Thuật Holography: Holography, một kỹ thuật ghi hình 3D, dựa vào hiện tượng giao thoa ánh sáng. Trong đó, các sóng ánh sáng giao thoa với nhau để tạo ra hình ảnh ba chiều chi tiết, được ứng dụng trong y học, nghệ thuật, và bảo mật.
- Kiểm Tra Không Phá Hủy (NDT): Hiện tượng giao thoa sóng siêu âm được sử dụng trong công nghệ kiểm tra không phá hủy để phát hiện các khuyết tật bên trong vật liệu mà không làm hỏng chúng. Đây là kỹ thuật quan trọng trong ngành hàng không, xây dựng, và sản xuất.
- Điều Hướng Sóng: Trong kỹ thuật radar và sonar, giao thoa sóng được dùng để xác định vị trí và hình dạng của các vật thể bằng cách phân tích các sóng phản xạ. Ứng dụng này rất quan trọng trong quân sự, hàng hải, và các ngành khoa học môi trường.
- Giao Thoa Ánh Sáng Trong Kính Hiển Vi: Các kính hiển vi giao thoa (interferometer microscopes) sử dụng nguyên lý giao thoa ánh sáng để đo đạc các chi tiết cực nhỏ với độ chính xác cao, được ứng dụng rộng rãi trong nghiên cứu khoa học và công nghệ nano.
- Nghiên Cứu Hiện Tượng Tự Nhiên: Giao thoa sóng nước giúp hiểu rõ hơn về các hiện tượng sóng biển, bao gồm sóng thần và sóng đứng, từ đó hỗ trợ trong công tác dự báo và phòng chống thiên tai.
- Phát Triển Công Nghệ Laser: Hiện tượng giao thoa sóng ánh sáng là cơ sở cho việc phát triển các công nghệ laser tiên tiến, được sử dụng trong y học, truyền thông, và công nghệ vũ khí.
- Tạo Mẫu Sóng: Các mô hình sóng nước và mô phỏng giao thoa sóng giúp các kỹ sư và nhà khoa học hiểu rõ hơn về các hiện tượng động lực học chất lỏng, phục vụ cho việc thiết kế công trình trên biển và nghiên cứu môi trường.
Những ứng dụng này không chỉ giúp nâng cao hiệu quả trong nghiên cứu và công nghệ, mà còn mang lại những cải tiến quan trọng trong đời sống hàng ngày và công nghiệp.

10 Dạng Bài Tập Về Giao Thoa Sóng Ở Mặt Nước
- Bài Tập 1: Cho hai nguồn sóng đồng bộ \(S_1\) và \(S_2\) cách nhau 20 cm. Sóng phát ra có bước sóng \(\lambda = 4\) cm. Tính khoảng cách từ \(S_1\) đến điểm giao thoa có cực đại thứ ba.
- Bài Tập 2: Xác định vị trí của các điểm có biên độ dao động bằng không trên mặt nước khi hai nguồn sóng đồng bộ có khoảng cách giữa chúng là 30 cm và bước sóng là 6 cm.
- Bài Tập 3: Với hai nguồn sóng phát đồng pha, khoảng cách giữa hai nguồn là 15 cm và bước sóng là 5 cm. Tính số vân giao thoa cực đại xuất hiện trên đường thẳng nối hai nguồn.
- Bài Tập 4: Hai nguồn sóng cách nhau 40 cm phát ra sóng với bước sóng 8 cm. Xác định số điểm giao thoa có biên độ cực tiểu trên mặt nước.
- Bài Tập 5: Hai nguồn sóng đồng pha cách nhau 25 cm. Tính khoảng cách giữa các vân giao thoa cực đại khi bước sóng của sóng là 5 cm.
- Bài Tập 6: Tìm khoảng cách từ nguồn sóng đến điểm giao thoa có biên độ dao động bằng không, biết rằng khoảng cách giữa hai nguồn sóng là 18 cm và bước sóng là 3 cm.
- Bài Tập 7: Cho hai nguồn sóng \(S_1\) và \(S_2\) cách nhau 35 cm và phát ra sóng với bước sóng 7 cm. Tính vị trí của các điểm trên mặt nước mà tại đó sóng bị triệt tiêu.
- Bài Tập 8: Hai nguồn sóng cách nhau 50 cm, phát ra sóng đồng bộ với bước sóng 10 cm. Tính số điểm giao thoa có biên độ cực đại xuất hiện trên đường tròn bán kính 30 cm xung quanh một trong hai nguồn.
- Bài Tập 9: Với hai nguồn sóng cách nhau 45 cm và bước sóng là 9 cm, tính vị trí của các vân giao thoa cực đại và cực tiểu trên mặt nước.
- Bài Tập 10: Hai nguồn sóng đồng pha cách nhau 60 cm, phát ra sóng với bước sóng 12 cm. Xác định vị trí các điểm có biên độ dao động bằng không trên mặt nước và giải thích lý do.
Các bài tập trên cung cấp cơ hội thực hành và hiểu sâu hơn về hiện tượng giao thoa sóng ở mặt nước, từ đó củng cố kiến thức lý thuyết và ứng dụng thực tiễn.
Dạng 1: Tính Bước Sóng Dựa Trên Khoảng Cách Giữa Các Vân Giao Thoa
Trong thí nghiệm giao thoa sóng ở mặt nước, hiện tượng giao thoa xảy ra khi hai hoặc nhiều sóng gặp nhau và chồng chất lên nhau. Kết quả của sự chồng chất này là sự hình thành các vân giao thoa, bao gồm các vân sáng (cực đại) và vân tối (cực tiểu). Các vân này được quan sát rõ ràng trên mặt nước, nơi mà sự giao thoa sóng diễn ra.
1. Nguyên lý giao thoa sóng
Giao thoa sóng là hiện tượng xảy ra khi hai sóng kết hợp với nhau, dẫn đến sự hình thành các điểm có biên độ lớn nhất (cực đại) và nhỏ nhất (cực tiểu). Các điểm cực đại hình thành ở những vị trí mà hai sóng tăng cường lẫn nhau, tức là chúng có cùng pha (sóng đạt cực đại cùng lúc). Ngược lại, các điểm cực tiểu hình thành ở những nơi hai sóng triệt tiêu lẫn nhau (sóng này đạt cực đại khi sóng kia đạt cực tiểu).
Bước sóng (\(\lambda\)) là khoảng cách giữa hai điểm liên tiếp có cùng pha, chẳng hạn như giữa hai đỉnh sóng liên tiếp hoặc hai đáy sóng liên tiếp.
2. Vân giao thoa
Trên mặt nước, các vân giao thoa hình thành là kết quả của sự giao thoa giữa hai sóng phát ra từ hai nguồn điểm khác nhau. Các vân sáng là những nơi có biên độ sóng lớn nhất, còn các vân tối là nơi biên độ sóng nhỏ nhất. Khoảng cách giữa các vân sáng hoặc các vân tối liên tiếp chính là một đặc trưng quan trọng để xác định bước sóng.
Khoảng cách giữa các vân giao thoa phụ thuộc vào các yếu tố như khoảng cách giữa hai nguồn sóng, bước sóng của sóng, và khoảng cách từ nguồn đến màn quan sát.
3. Công thức tính bước sóng
Bước sóng có thể được tính bằng công thức sau:
\[
\lambda = \frac{d \cdot a}{D}
\]
Trong đó:
- \(d\) là khoảng cách giữa hai vân giao thoa liên tiếp (có thể là giữa hai vân sáng hoặc hai vân tối).
- \(a\) là khoảng cách giữa hai nguồn sóng.
- \(D\) là khoảng cách từ các nguồn đến màn quan sát.
4. Ý nghĩa của bước sóng
Bước sóng là một đặc trưng quan trọng của sóng, cho biết khoảng cách giữa hai điểm liên tiếp trên sóng có cùng pha. Trong thí nghiệm giao thoa sóng ở mặt nước, việc xác định chính xác bước sóng giúp ta hiểu rõ hơn về tính chất của sóng, chẳng hạn như tần số và tốc độ truyền sóng.
5. Ứng dụng của lý thuyết giao thoa
Lý thuyết giao thoa sóng không chỉ quan trọng trong vật lý lý thuyết mà còn có nhiều ứng dụng thực tiễn trong các lĩnh vực như kỹ thuật, công nghệ thông tin và truyền thông, và giáo dục. Hiểu rõ hiện tượng giao thoa giúp cải thiện các thiết bị sóng, từ các bộ lọc sóng đến các thiết bị thu phát tín hiệu.
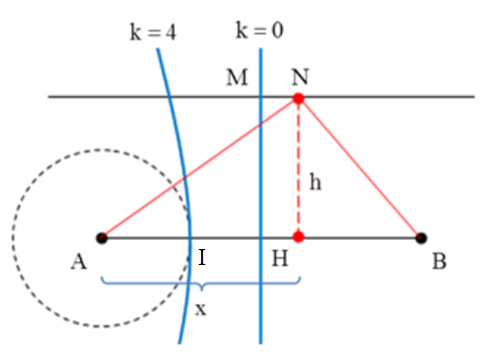
Dạng 2: Xác Định Số Điểm Cực Đại Trên Đoạn Thẳng Giữa Hai Nguồn
Trong thí nghiệm giao thoa sóng ở mặt nước, hai nguồn sóng kết hợp cùng pha được đặt tại hai điểm A và B trên mặt nước. Để xác định số điểm cực đại trên đoạn thẳng AB, ta cần phân tích điều kiện giao thoa và sử dụng công thức liên quan.
1. Điều kiện giao thoa cực đại
Các điểm dao động với biên độ cực đại trên đoạn thẳng giữa hai nguồn xảy ra khi hiệu đường đi của sóng từ hai nguồn đến điểm đó bằng một bội số nguyên của bước sóng:
\[ \Delta d = |d_1 - d_2| = k\lambda \]
Trong đó:
- \(d_1\), \(d_2\) là khoảng cách từ điểm đang xét đến hai nguồn A và B.
- \(\lambda\) là bước sóng của sóng trên mặt nước.
- \(k\) là số nguyên (0, ±1, ±2, ...).
2. Xác định số điểm cực đại
Trên đoạn thẳng AB, số điểm cực đại sẽ được xác định bằng cách tính toán giá trị của \(k\) sao cho điểm nằm trên đoạn AB thỏa mãn điều kiện trên:
- Xác định khoảng cách giữa hai nguồn \(AB = d\).
- Tính giá trị \(k\) lớn nhất và nhỏ nhất sao cho \(k\lambda\) nằm trong khoảng từ 0 đến \(d\).
- Số điểm cực đại là tổng số giá trị của \(k\) có thể có.
3. Ví dụ minh họa
Giả sử hai nguồn A và B dao động cùng pha, cách nhau một khoảng \(d = 16\) cm. Bước sóng của sóng trên mặt nước là \(\lambda = 3\) cm. Ta có:
\[ k\lambda = 3k \quad \text{với} \quad -d \leq 3k \leq d \]
Từ đó, giá trị của \(k\) sẽ nằm trong khoảng:
\[ -\frac{16}{3} \leq k \leq \frac{16}{3} \approx -5.33 \leq k \leq 5.33 \]
Vậy \(k\) có thể nhận các giá trị từ -5 đến 5, tương ứng với 11 điểm cực đại (bao gồm cả k = 0).
Như vậy, số điểm cực đại trên đoạn thẳng AB là 11.
4. Kết luận
Như vậy, bằng cách sử dụng điều kiện giao thoa cực đại và tính toán các giá trị khả thi của \(k\), ta có thể xác định được số điểm cực đại trên đoạn thẳng giữa hai nguồn. Đây là một trong những ứng dụng quan trọng của lý thuyết giao thoa sóng trong việc phân tích các hiện tượng vật lý trên mặt nước.

Dạng 3: Tính Tốc Độ Truyền Sóng Dựa Trên Các Thông Số Đã Cho
Trong thí nghiệm giao thoa sóng ở mặt nước, tốc độ truyền sóng \( v \) có thể được tính toán dựa trên các thông số đã cho, như tần số \( f \) và bước sóng \( \lambda \). Công thức tính tốc độ truyền sóng là:
\[
v = f \cdot \lambda
\]
Giả sử trong thí nghiệm, chúng ta có tần số dao động của nguồn là \( f = 15 \, \text{Hz} \) và bước sóng là \( \lambda = 0.4 \, \text{m} \). Khi đó, tốc độ truyền sóng sẽ được tính như sau:
\[
v = 15 \, \text{Hz} \times 0.4 \, \text{m} = 6 \, \text{m/s}
\]
Bước sóng \( \lambda \) có thể được xác định thông qua khoảng cách giữa hai điểm cực đại hoặc cực tiểu liên tiếp trên mặt nước. Nếu biết khoảng cách này và tần số của sóng, ta dễ dàng suy ra tốc độ truyền sóng.
Các bước tính toán chi tiết:
- Xác định tần số dao động \( f \): Đây là tần số dao động của nguồn sóng, được cho trong đề bài hoặc đo được.
- Xác định bước sóng \( \lambda \): Bước sóng có thể được xác định bằng cách đo khoảng cách giữa hai điểm cực đại hoặc cực tiểu liên tiếp và nhân với hằng số tỷ lệ nếu có.
- Tính tốc độ truyền sóng: Áp dụng công thức \( v = f \cdot \lambda \) để tìm tốc độ truyền sóng.
Ví dụ, nếu hai điểm cực đại liên tiếp trên đoạn thẳng giữa hai nguồn cách nhau \( d = 0.5 \, \text{m} \) và tần số sóng là \( f = 20 \, \text{Hz} \), thì tốc độ truyền sóng sẽ là:
\[
v = 20 \, \text{Hz} \times 0.5 \, \text{m} = 10 \, \text{m/s}
\]
Qua đó, ta thấy rằng tốc độ truyền sóng trên mặt nước phụ thuộc trực tiếp vào tần số của nguồn và bước sóng được tạo ra.
Dạng 4: Xác Định Khoảng Cách Giữa Hai Nguồn Sóng
Trong thí nghiệm giao thoa sóng trên mặt nước, việc xác định khoảng cách giữa hai nguồn sóng đóng vai trò quan trọng trong việc phân tích hiện tượng giao thoa. Bước sóng (\(\lambda\)) và khoảng cách giữa hai nguồn (\(d\)) là những yếu tố chính quyết định đến số điểm cực đại và cực tiểu xuất hiện trên đoạn thẳng giữa hai nguồn.
1. Công thức tính khoảng cách giữa hai nguồn
Khoảng cách giữa hai nguồn sóng có thể được xác định thông qua các thông số như tần số (\(f\)) của sóng, vận tốc truyền sóng (\(v\)), và số điểm cực đại (hoặc cực tiểu) trên đoạn thẳng giữa hai nguồn.
Công thức tính khoảng cách giữa hai nguồn sóng là:
trong đó:
- \(d\) là khoảng cách giữa hai nguồn.
- \(\lambda\) là bước sóng của sóng trên mặt nước, được tính bằng công thức \(\lambda = \frac{v}{f}\).
- \(k\) là số điểm cực đại (hoặc cực tiểu) xuất hiện trên đoạn thẳng giữa hai nguồn.
2. Ví dụ minh họa
Giả sử trong một thí nghiệm giao thoa sóng nước, khoảng cách giữa hai nguồn sóng kết hợp \(O_1\) và \(O_2\) là 36 cm. Tần số dao động của hai nguồn là \(f = 5 \, Hz\), và vận tốc truyền sóng trên mặt nước là \(v = 40 \, cm/s\). Để tính khoảng cách giữa hai nguồn, ta thực hiện các bước sau:
- Tính bước sóng: \[ \lambda = \frac{v}{f} = \frac{40 \, cm/s}{5 \, Hz} = 8 \, cm \]
- Sử dụng công thức xác định khoảng cách giữa hai nguồn: \[ d = \frac{k \cdot \lambda}{2} = \frac{36 \, cm}{2} = 18 \, cm \]
Như vậy, khoảng cách giữa hai nguồn sóng trong thí nghiệm này là 18 cm.
3. Kết luận
Việc xác định chính xác khoảng cách giữa hai nguồn sóng là rất quan trọng trong việc hiểu và dự đoán các hiện tượng giao thoa xảy ra trên mặt nước. Công thức và quy trình tính toán được minh họa ở trên là cơ sở để thực hiện các thí nghiệm và bài tập liên quan đến giao thoa sóng.

Dạng 5: Phân Tích Tác Động Của Tần Số Sóng Đến Hiện Tượng Giao Thoa
Trong thí nghiệm giao thoa sóng trên mặt nước, tần số sóng là một yếu tố quan trọng quyết định đến việc quan sát các hiện tượng giao thoa. Dưới đây là phân tích chi tiết về tác động của tần số sóng đến hiện tượng giao thoa:
1. Ảnh Hưởng Của Tần Số Đến Bước Sóng (\(\lambda\))
Tần số sóng (\(f\)) và bước sóng (\(\lambda\)) có mối quan hệ nghịch đảo với nhau, được biểu diễn qua công thức:
\[
\lambda = \frac{v}{f}
\]
trong đó:
- \(v\) là tốc độ truyền sóng trên mặt nước.
- \(f\) là tần số của sóng.
Khi tần số tăng, bước sóng sẽ giảm và ngược lại. Điều này có nghĩa là các vân giao thoa (cả cực đại và cực tiểu) sẽ trở nên gần nhau hơn khi tần số tăng, làm cho hiện tượng giao thoa trở nên dễ quan sát hơn.
2. Tác Động Đến Biên Độ Dao Động
Biên độ dao động của các điểm trên mặt nước cũng chịu tác động từ tần số sóng. Khi tần số tăng, năng lượng của sóng tăng, làm cho biên độ dao động tại các điểm cực đại có thể lớn hơn. Điều này dẫn đến các vân cực đại rõ ràng hơn trên mặt nước.
3. Ứng Dụng Và Ý Nghĩa
Việc điều chỉnh tần số sóng trong thí nghiệm không chỉ giúp làm rõ hiện tượng giao thoa mà còn có ứng dụng thực tế trong các ngành công nghiệp như thiết kế hệ thống chống sóng cho cầu cống hoặc trong các nghiên cứu về sóng biển.
Như vậy, tần số sóng là một trong những yếu tố chủ chốt trong việc điều chỉnh và quan sát hiện tượng giao thoa sóng trên mặt nước. Hiểu rõ tác động của tần số giúp người thực hiện thí nghiệm tối ưu hóa quá trình quan sát và ghi nhận kết quả một cách chính xác nhất.
Dạng 6: Xác Định Khoảng Cách Giữa Hai Vân Liên Tiếp
Trong thí nghiệm giao thoa sóng ở mặt nước, khoảng cách giữa hai vân giao thoa liên tiếp (có thể là hai vân cực đại hoặc hai vân cực tiểu) là một thông số quan trọng để xác định các tính chất của sóng.
Để xác định khoảng cách này, ta cần dựa vào bước sóng \(\lambda\) của sóng trên mặt nước và khoảng cách giữa hai nguồn sóng \(d\). Công thức cơ bản để tính khoảng cách giữa hai vân liên tiếp là:
\[
\Delta x = \frac{\lambda \cdot D}{d}
\]
Trong đó:
- \(\Delta x\): Khoảng cách giữa hai vân giao thoa liên tiếp.
- \(\lambda\): Bước sóng của sóng trên mặt nước.
- \(D\): Khoảng cách từ các nguồn sóng đến màn quan sát.
- \(d\): Khoảng cách giữa hai nguồn sóng.
Quá trình xác định khoảng cách giữa hai vân liên tiếp có thể được thực hiện theo các bước sau:
- Xác định bước sóng \(\lambda\) của sóng trên mặt nước bằng cách đo trực tiếp hoặc sử dụng các thông tin liên quan khác.
- Đo khoảng cách \(d\) giữa hai nguồn sóng.
- Đo khoảng cách \(D\) từ nguồn sóng đến màn quan sát.
- Sử dụng công thức trên để tính toán khoảng cách giữa hai vân giao thoa liên tiếp \(\Delta x\).
Ví dụ: Giả sử trong một thí nghiệm, ta có bước sóng của sóng là \(\lambda = 4 \, \text{cm}\), khoảng cách giữa hai nguồn là \(d = 10 \, \text{cm}\), và khoảng cách từ nguồn đến màn là \(D = 100 \, \text{cm}\). Khi đó, khoảng cách giữa hai vân liên tiếp được tính như sau:
\[
\Delta x = \frac{4 \, \text{cm} \times 100 \, \text{cm}}{10 \, \text{cm}} = 40 \, \text{cm}
\]
Như vậy, khoảng cách giữa hai vân liên tiếp trong thí nghiệm này là 40 cm.
Dạng 7: Tính Toán Biên Độ Của Sóng Tại Các Vị Trí Khác Nhau
Trong thí nghiệm giao thoa sóng trên mặt nước, việc tính toán biên độ sóng tại các vị trí khác nhau là một phần quan trọng để hiểu rõ hơn về hiện tượng này. Dưới đây là cách tiếp cận để tính toán biên độ của sóng tại một điểm bất kỳ M trên mặt nước, nơi có sự giao thoa của hai sóng xuất phát từ hai nguồn kết hợp A và B.
- Bước 1: Xác định phương trình sóng từ hai nguồn A và B đến điểm M
Giả sử phương trình sóng từ nguồn A đến M là:
\[ u_{AM} = A \cos \left( \frac{2\pi}{T} \left(t - \frac{d_1}{v}\right) \right) \]
Tương tự, phương trình sóng từ nguồn B đến M là:
\[ u_{BM} = A \cos \left( \frac{2\pi}{T} \left(t - \frac{d_2}{v}\right) \right) \]
- Bước 2: Phương trình sóng tổng hợp tại điểm M
Tại điểm M, biên độ tổng hợp của sóng được tính bằng cách cộng phương trình của hai sóng này:
\[ u_M = u_{AM} + u_{BM} = A \cos \left( \frac{2\pi}{T} \left(t - \frac{d_1}{v}\right) \right) + A \cos \left( \frac{2\pi}{T} \left(t - \frac{d_2}{v}\right) \right) \]
Sử dụng công thức cộng lượng giác, ta có thể rút gọn phương trình trên thành:
\[ u_M = 2A \cos \left( \frac{\pi(d_2 - d_1)}{\lambda} \right) \cos \left( \frac{2\pi}{T} \left(t - \frac{d_1 + d_2}{2v}\right) \right) \]
- Bước 3: Tính toán biên độ sóng tại điểm M
Biên độ dao động tại điểm M được xác định bởi biểu thức:
\[ A_M = 2A \left| \cos \left( \frac{\pi (d_2 - d_1)}{\lambda} \right) \right| \]
Biên độ này phụ thuộc vào sự khác biệt về đường đi giữa hai sóng từ các nguồn đến điểm M.
Qua quá trình tính toán, ta thấy rằng biên độ sóng tại một điểm không chỉ phụ thuộc vào biên độ ban đầu của sóng từ các nguồn mà còn bị ảnh hưởng bởi sự chênh lệch về khoảng cách từ các nguồn đến điểm đó. Điều này tạo ra các vùng có biên độ dao động lớn (cực đại) và các vùng có biên độ dao động nhỏ (cực tiểu) trên mặt nước.
Dạng 8: Phân Tích Ảnh Hưởng Của Biên Độ Dao Động Đến Hiện Tượng Giao Thoa
Trong thí nghiệm giao thoa sóng ở mặt nước, biên độ dao động của các nguồn phát sóng đóng vai trò quan trọng trong việc xác định hình dạng và độ rõ nét của các vân giao thoa. Để phân tích ảnh hưởng của biên độ dao động đến hiện tượng giao thoa, ta cần chú ý các yếu tố sau:
- Biên độ dao động: Biên độ càng lớn, năng lượng truyền sóng càng mạnh, dẫn đến các vân giao thoa rõ ràng và sắc nét hơn. Ngược lại, nếu biên độ dao động nhỏ, các vân giao thoa sẽ mờ nhạt và khó quan sát.
- Độ tương phản giữa các vân: Khi biên độ của các nguồn dao động tăng lên, sự khác biệt về cường độ giữa các vân cực đại và cực tiểu cũng tăng, làm cho các vân giao thoa trở nên rõ nét hơn. Điều này được thể hiện rõ trong các thí nghiệm với hai nguồn kết hợp có biên độ lớn, nơi mà các vân sáng tối được phân biệt rõ rệt.
- Sự ổn định của nguồn phát: Nếu biên độ dao động không ổn định, hiện tượng giao thoa có thể bị ảnh hưởng, dẫn đến việc các vân giao thoa có thể dịch chuyển hoặc thay đổi hình dạng theo thời gian.
Do đó, việc điều chỉnh biên độ dao động là một yếu tố quan trọng trong việc thiết kế và thực hiện các thí nghiệm giao thoa sóng, nhằm đảm bảo thu được kết quả chính xác và dễ quan sát.
Dạng 9: Tính Số Vân Giao Thoa Trên Một Đoạn Xác Định
Trong thí nghiệm giao thoa sóng ở mặt nước, việc tính số vân giao thoa trên một đoạn xác định giúp chúng ta hiểu rõ hơn về cấu trúc và tính chất của sóng. Dưới đây là quy trình tính toán số vân giao thoa trên một đoạn xác định:
- Xác định khoảng cách giữa hai nguồn sóng \(d\).
- Đo khoảng cách từ một điểm bất kỳ trên mặt nước đến hai nguồn sóng đó \(r_1\) và \(r_2\).
- Tính hiệu đường đi của sóng từ hai nguồn đến điểm đó: \(\Delta r = r_1 - r_2\).
- Xác định bước sóng \(\lambda\) của sóng.
- Số vân giao thoa \(n\) trên đoạn \(L\) giữa hai điểm có hiệu đường đi sóng \(\Delta r\) là:
\[ n = \frac{L}{\lambda} \]
Trong đó:
- \(L\) là chiều dài đoạn thẳng giữa hai điểm mà bạn muốn xác định số vân.
- \(\lambda\) là bước sóng của sóng giao thoa.
Ví dụ, nếu đoạn \(L\) là 10 cm và bước sóng \(\lambda\) là 2 cm, số vân giao thoa trên đoạn này sẽ là:
\[ n = \frac{10}{2} = 5 \]
Như vậy, sẽ có 5 vân giao thoa xuất hiện trên đoạn thẳng này. Điều này cho phép ta có thể dự đoán và kiểm soát kết quả thí nghiệm, từ đó phục vụ cho việc nghiên cứu và giảng dạy.
Dạng 10: So Sánh Kết Quả Thực Nghiệm Với Lý Thuyết
Trong thí nghiệm giao thoa sóng ở mặt nước, việc so sánh kết quả thực nghiệm với lý thuyết giúp kiểm chứng tính đúng đắn của các công thức và mô hình sóng đã học. Dưới đây là các bước để thực hiện so sánh này:
- Thu thập kết quả thực nghiệm:
- Ghi lại các thông số như bước sóng, tần số, và biên độ của sóng từ thí nghiệm.
- Đo lường khoảng cách giữa các vân giao thoa và so sánh với dự đoán lý thuyết.
- Áp dụng công thức lý thuyết:
- Sử dụng công thức giao thoa để tính toán các thông số dự kiến như khoảng cách giữa các vân, số vân trên đoạn thẳng, v.v.
- Công thức cơ bản để tính khoảng cách giữa các vân giao thoa là:
\[ \Delta x = \frac{\lambda D}{d} \]
Trong đó:- \(\Delta x\) là khoảng cách giữa hai vân sáng liên tiếp.
- \(\lambda\) là bước sóng.
- \(D\) là khoảng cách từ hai nguồn sóng đến màn quan sát.
- \(d\) là khoảng cách giữa hai nguồn sóng.
- So sánh và phân tích:
- So sánh các giá trị thực nghiệm với các giá trị tính toán theo lý thuyết.
- Nếu có sự chênh lệch, phân tích nguyên nhân có thể do sai số trong quá trình đo lường, hiệu ứng môi trường, hoặc giả định lý thuyết.
- Kết luận:
Nếu kết quả thực nghiệm khớp với lý thuyết trong giới hạn sai số chấp nhận được, ta có thể kết luận rằng lý thuyết sóng đã áp dụng đúng. Nếu có sự khác biệt lớn, cần xem xét lại các giả định và phương pháp thực hiện thí nghiệm.
So sánh kết quả thực nghiệm với lý thuyết không chỉ giúp xác minh tính chính xác của mô hình lý thuyết mà còn giúp cải thiện kỹ năng thực nghiệm và hiểu rõ hơn về hiện tượng giao thoa sóng.