Lý Thuyết Giao Thoa Ánh Sáng: Khám Phá Hiện Tượng Kỳ Diệu Trong Vật Lý

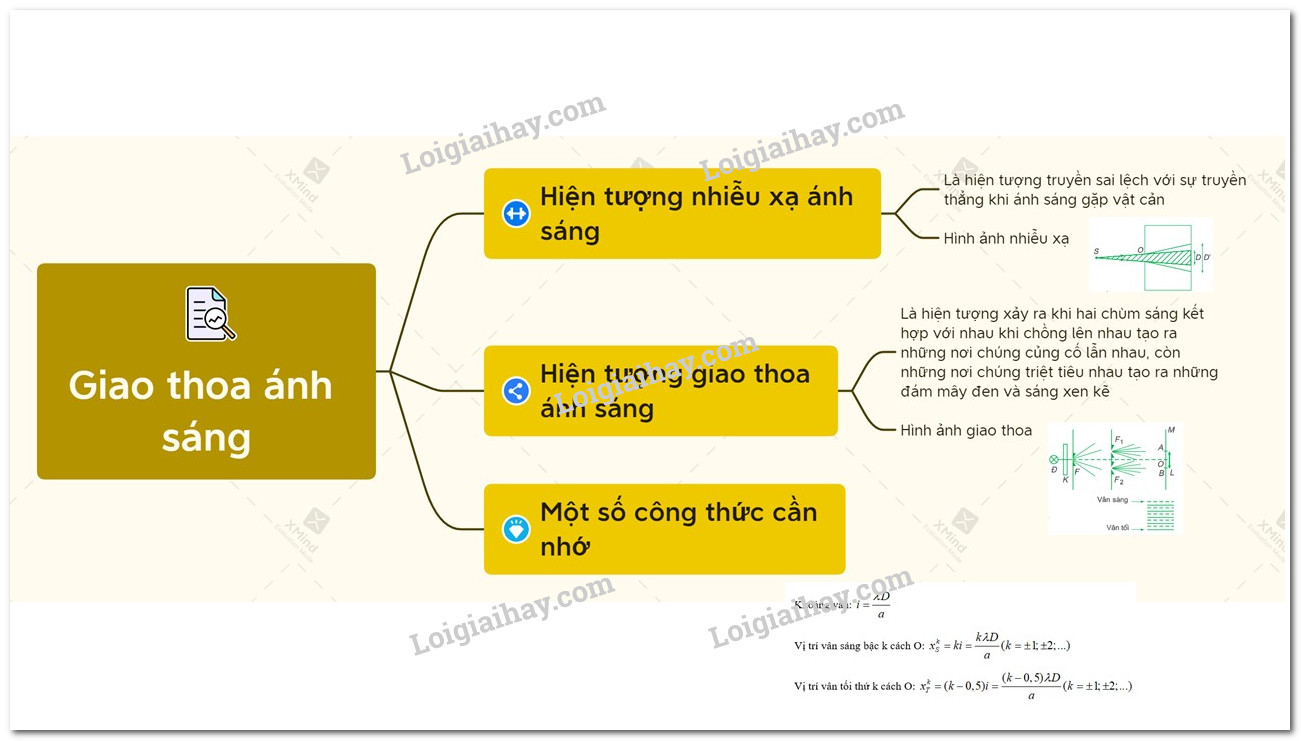
Giao thoa ánh sáng là một hiện tượng quan trọng trong vật lý, minh chứng cho tính chất sóng của ánh sáng. Hiện tượng này xảy ra khi hai hoặc nhiều chùm ánh sáng kết hợp với nhau, tạo ra các vùng sáng tối do sự chồng chất của các sóng ánh sáng.

1. Thí Nghiệm Y-âng

Thí nghiệm Y-âng là một trong những thí nghiệm nổi tiếng nhất về giao thoa ánh sáng. Thí nghiệm được thực hiện bằng cách chiếu ánh sáng qua hai khe hẹp song song, tạo ra các vân giao thoa trên màn hứng.

• Chuẩn bị nguồn sáng đơn sắc (thường là ánh sáng từ laser).
• Chiếu ánh sáng qua hai khe hẹp song song.
• Quan sát các vân sáng và vân tối xuất hiện trên màn hứng.

2. Điều Kiện Để Xảy Ra Giao Thoa Ánh Sáng

• Hai nguồn sáng phải là nguồn kết hợp, tức là có cùng tần số và hiệu số pha không đổi theo thời gian.
• Hai nguồn sáng phải có độ lệch pha nhỏ hoặc bằng một số nguyên lần bước sóng để tạo ra vân sáng.

3. Vị Trí Các Vân Sáng, Vân Tối

Các vân sáng và vân tối trên màn giao thoa được xác định như sau:

• Vân sáng: Xuất hiện tại các vị trí có hiệu đường đi của hai sóng bằng một số nguyên lần bước sóng: \[ d_2 - d_1 = k \lambda \]
• Vân tối: Xuất hiện tại các vị trí có hiệu đường đi của hai sóng bằng một số lẻ lần nửa bước sóng: \[ d_2 - d_1 = \left( k + \frac{1}{2} \right) \lambda \]

4. Công Thức Tính Khoảng Vân

Khoảng vân (khoảng cách giữa hai vân sáng liên tiếp hoặc hai vân tối liên tiếp) được tính bằng công thức:

\[ i = \frac{\lambda D}{a} \]

Trong đó:

• \( i \) là khoảng vân
• \( \lambda \) là bước sóng ánh sáng
• \( D \) là khoảng cách từ khe đến màn
• \( a \) là khoảng cách giữa hai khe

5. Ứng Dụng Của Hiện Tượng Giao Thoa Ánh Sáng

Hiện tượng giao thoa ánh sáng không chỉ là một minh chứng quan trọng cho tính chất sóng của ánh sáng mà còn có nhiều ứng dụng thực tiễn trong các lĩnh vực khác nhau như:

• Thiết kế các thiết bị quang học, như máy quang phổ và các cảm biến quang học.
• Trong công nghệ laze, giao thoa ánh sáng được sử dụng để tạo ra các mô hình quang học tinh vi, phục vụ cho nhiều ứng dụng trong khoa học và công nghệ.

Giao thoa ánh sáng là hiện tượng xảy ra khi hai chùm sáng kết hợp gặp nhau, tạo ra các vân sáng và vân tối xen kẽ trên màn quan sát. Để hiện tượng giao thoa xảy ra, cần có hai nguồn sáng kết hợp, tức là hai nguồn phát ra sóng ánh sáng có cùng bước sóng và độ lệch pha không đổi theo thời gian.

Trong thí nghiệm giao thoa ánh sáng, hiệu quang lộ giữa hai chùm sáng tại điểm quan sát quyết định sự xuất hiện của vân sáng hay vân tối. Cụ thể, vị trí của các vân sáng trên màn có thể được xác định qua công thức:

Trong đó, \(x_k\) là vị trí vân sáng bậc \(k\), \(\lambda\) là bước sóng ánh sáng, \(D\) là khoảng cách từ khe đến màn, và \(a\) là khoảng cách giữa hai khe.

Khoảng cách giữa hai vân sáng liên tiếp, gọi là khoảng vân, được tính theo công thức:

Hiện tượng giao thoa ánh sáng không chỉ chứng minh được tính chất sóng của ánh sáng mà còn là nền tảng cho nhiều ứng dụng trong đo lường bước sóng và nghiên cứu quang học hiện đại.

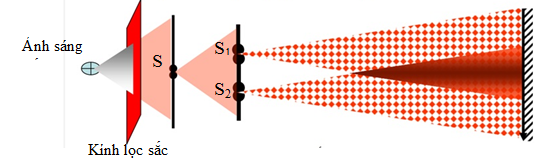
Thí nghiệm Y-âng là một trong những thí nghiệm quan trọng nhất trong lịch sử vật lý, chứng minh tính chất sóng của ánh sáng. Thí nghiệm này được thực hiện lần đầu tiên bởi nhà vật lý người Anh Thomas Young vào năm 1801.

Trong thí nghiệm Y-âng, một nguồn sáng đơn sắc (thường là ánh sáng từ đèn Natri) được chiếu qua một khe hẹp để tạo ra một chùm sáng song song. Chùm sáng này sau đó đi qua hai khe hẹp song song rất gần nhau, tạo ra hai chùm sáng mới. Hai chùm sáng này sau đó giao thoa với nhau trên một màn hứng, tạo ra các vân sáng và vân tối xen kẽ.

Vị trí các vân sáng và vân tối trên màn có thể được xác định bằng công thức:

Trong đó:

• \(\lambda\) là bước sóng ánh sáng.
• \(D\) là khoảng cách từ hai khe đến màn.
• \(a\) là khoảng cách giữa hai khe.
• \(x_k\) là vị trí của vân sáng bậc \(k\) trên màn.

Khoảng cách giữa hai vân sáng liên tiếp, gọi là khoảng vân, được xác định bởi:

Thí nghiệm Y-âng không chỉ chứng minh được bản chất sóng của ánh sáng mà còn là cơ sở cho nhiều thí nghiệm quang học hiện đại. Nó cũng giúp đo lường chính xác bước sóng của ánh sáng và khẳng định rằng ánh sáng là sóng cơ học truyền qua môi trường.

Giao thoa ánh sáng là hiện tượng quan trọng trong quang học, xảy ra khi hai chùm sáng gặp nhau và tạo ra các vân sáng, vân tối. Để giao thoa ánh sáng xảy ra, cần thỏa mãn các điều kiện sau:

• Nguồn sáng kết hợp: Hai chùm sáng phải xuất phát từ hai nguồn sáng kết hợp, tức là hai nguồn này phải có cùng tần số (hay bước sóng \(\lambda\)) và độ lệch pha không đổi theo thời gian. Nếu các nguồn sáng không kết hợp, hiện tượng giao thoa sẽ không xuất hiện rõ ràng.
• Hai chùm sáng đồng pha hoặc có độ lệch pha không đổi: Để các vân giao thoa rõ ràng, hai chùm sáng phải đồng pha hoặc có độ lệch pha không đổi. Nếu độ lệch pha thay đổi ngẫu nhiên, các vân giao thoa sẽ bị mờ và khó nhận biết.
• Ánh sáng đơn sắc: Sử dụng ánh sáng đơn sắc giúp các vân giao thoa rõ ràng hơn. Nếu sử dụng ánh sáng trắng (có nhiều bước sóng khác nhau), các vân giao thoa có thể bị chồng lấn và khó phân biệt.
• Khoảng cách giữa hai nguồn sáng: Khoảng cách giữa hai nguồn sáng càng nhỏ thì khoảng vân càng lớn, giúp các vân giao thoa dễ dàng nhận thấy hơn. Trong thí nghiệm Y-âng, khoảng cách giữa hai khe thường rất nhỏ để đảm bảo giao thoa ánh sáng xảy ra.
• Điều kiện thí nghiệm ổn định: Để quan sát rõ hiện tượng giao thoa, cần đảm bảo điều kiện thí nghiệm ổn định, không có sự dao động hoặc nhiễu loạn từ môi trường bên ngoài.

Những điều kiện trên là cơ sở để hiện tượng giao thoa ánh sáng xảy ra và được quan sát rõ ràng. Hiện tượng này không chỉ chứng minh tính chất sóng của ánh sáng mà còn giúp các nhà khoa học nghiên cứu sâu hơn về tính chất và ứng dụng của ánh sáng trong nhiều lĩnh vực khác nhau.

Trong hiện tượng giao thoa ánh sáng, các vân sáng và vân tối được hình thành do sự chồng chập của hai chùm sáng kết hợp. Vị trí của các vân này trên màn quan sát được xác định bởi các điều kiện giao thoa cụ thể.

Các vân sáng xuất hiện ở những điểm mà hai sóng sáng gặp nhau với độ lệch pha bằng bội số nguyên của bước sóng, tức là khi hiệu quang trình của hai sóng là một số nguyên lần bước sóng. Ngược lại, các vân tối xuất hiện ở những điểm mà hai sóng gặp nhau với độ lệch pha bằng một số lẻ của nửa bước sóng, tức là khi hiệu quang trình của hai sóng là một số lẻ của nửa bước sóng.

Vị trí của vân sáng và vân tối trên màn được tính theo công thức:

• Vị trí vân sáng: \[x_k = \frac{k \cdot \lambda \cdot D}{a}\] với \(k\) là số nguyên, \(\lambda\) là bước sóng ánh sáng, \(D\) là khoảng cách từ hai khe đến màn, và \(a\) là khoảng cách giữa hai khe sáng.
• Vị trí vân tối: \[x_{k'} = \frac{(k' + 0.5) \cdot \lambda \cdot D}{a}\] với \(k'\) là số nguyên, \(\lambda\) là bước sóng ánh sáng, \(D\) là khoảng cách từ hai khe đến màn, và \(a\) là khoảng cách giữa hai khe sáng.

Kết quả là trên màn, ta thấy một dãy các vân sáng và vân tối xen kẽ. Các vân sáng càng rõ ràng khi điều kiện giao thoa tốt, như ánh sáng đơn sắc và các nguồn sáng kết hợp đồng pha. Tính toán và hiểu được vị trí của các vân sáng, vân tối giúp ta xác định được các đặc tính của ánh sáng và ứng dụng trong nhiều lĩnh vực khác nhau.

Khoảng vân là một đại lượng quan trọng trong hiện tượng giao thoa ánh sáng, thể hiện khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp trên màn giao thoa. Khoảng vân phụ thuộc vào bước sóng ánh sáng, khoảng cách giữa hai khe sáng, và khoảng cách từ khe đến màn quan sát.

Công thức tính khoảng vân được xác định như sau:

• \[i = \frac{\lambda \cdot D}{a}\]
• Trong đó:
• \(\lambda\) là bước sóng ánh sáng
• \(D\) là khoảng cách từ khe đến màn
• \(a\) là khoảng cách giữa hai khe sáng
• \(i\) là khoảng vân, biểu thị khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp

Khoảng vân càng lớn khi bước sóng ánh sáng lớn hoặc khi khoảng cách từ khe đến màn lớn. Ngược lại, khoảng vân sẽ nhỏ hơn khi khoảng cách giữa hai khe tăng lên.

Trong thực tế, việc xác định khoảng vân cho phép các nhà vật lý đo lường và tính toán các đặc tính của sóng ánh sáng một cách chính xác. Thông qua thí nghiệm Y-âng và các thí nghiệm giao thoa khác, việc đo khoảng vân giúp kiểm chứng các lý thuyết về ánh sáng và sóng, từ đó ứng dụng trong nhiều lĩnh vực công nghệ hiện đại.

Hiện tượng giao thoa ánh sáng không chỉ là một khái niệm lý thuyết trong vật lý, mà còn có nhiều ứng dụng thực tiễn trong cuộc sống và công nghệ. Dưới đây là một số ứng dụng nổi bật của hiện tượng này:

• Kiểm tra chất lượng bề mặt: Giao thoa ánh sáng được sử dụng để kiểm tra độ phẳng và chất lượng bề mặt của các vật liệu, đặc biệt là trong sản xuất các thiết bị quang học như gương, thấu kính. Các thiết bị interferometer giúp xác định sai lệch bề mặt với độ chính xác cao bằng cách quan sát các vân giao thoa.
• Phân tích lớp màng mỏng: Hiện tượng giao thoa ánh sáng được áp dụng trong việc xác định độ dày và tính chất của các lớp màng mỏng, như lớp phủ quang học trên kính hoặc các lớp bảo vệ trên các bề mặt kim loại. Khi ánh sáng phản xạ từ các lớp màng này, sự giao thoa xảy ra tạo ra các mẫu vân sáng và tối giúp phân tích đặc tính của lớp màng.
• Công nghệ viễn thám: Trong lĩnh vực viễn thám, giao thoa ánh sáng giúp trong việc phát hiện và phân tích các hiện tượng tự nhiên trên bề mặt Trái Đất. Các cảm biến interferometer trên vệ tinh có thể thu thập thông tin về địa hình, độ cao và các thay đổi môi trường dựa trên các mẫu vân giao thoa được ghi nhận.
• Phát triển công nghệ laser: Giao thoa ánh sáng là nền tảng cho việc phát triển các công nghệ liên quan đến laser. Bằng cách điều khiển sự giao thoa, các nhà khoa học có thể tạo ra các chùm tia laser với cường độ và tính chất quang học mong muốn, ứng dụng trong y học, viễn thông, và các ngành công nghiệp khác.
• Ứng dụng trong y học: Giao thoa ánh sáng được sử dụng trong y học để chụp cắt lớp quang học (Optical Coherence Tomography - OCT), một phương pháp hình ảnh không xâm lấn được sử dụng để quét và tạo hình ảnh chi tiết của các mô bên trong cơ thể, đặc biệt là võng mạc mắt.

Các ứng dụng của hiện tượng giao thoa ánh sáng ngày càng đa dạng và quan trọng trong nhiều lĩnh vực, từ nghiên cứu khoa học cơ bản đến các ứng dụng công nghệ cao, góp phần cải thiện chất lượng cuộc sống và mở ra nhiều hướng phát triển mới.

Dưới đây là một số dạng bài tập phổ biến về hiện tượng giao thoa ánh sáng, giúp người học củng cố kiến thức và kỹ năng phân tích, giải quyết các vấn đề liên quan đến giao thoa ánh sáng.

7.1. Bài tập tính vị trí vân sáng, vân tối

• Xác định vị trí các vân sáng và vân tối trong thí nghiệm giao thoa ánh sáng đơn sắc, sử dụng công thức:

\[ x_m = \frac{m \cdot \lambda \cdot D}{d} \]

• Trong đó:
• \(x_m\) là vị trí của vân sáng hoặc vân tối thứ \(m\) trên màn.
• \(\lambda\) là bước sóng ánh sáng sử dụng.
• \(D\) là khoảng cách từ hai khe đến màn.
• \(d\) là khoảng cách giữa hai khe.
• \(m\) là bậc của vân sáng hoặc vân tối.

7.2. Bài tập tính khoảng vân

• Khi biết bước sóng ánh sáng và các tham số của thí nghiệm, tính khoảng vân (khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp) bằng công thức:

\[ i = \frac{\lambda \cdot D}{d} \]

• Áp dụng vào các trường hợp thực tế để tính toán khoảng vân trong các tình huống khác nhau.

7.3. Bài tập về thí nghiệm Y-âng

• Phân tích và giải bài tập liên quan đến thí nghiệm Y-âng, bao gồm việc xác định bước sóng của ánh sáng dựa trên các thông số thực nghiệm.
• Ứng dụng các công thức cơ bản để giải quyết các bài toán phức tạp hơn về giao thoa ánh sáng.

7.4. Bài tập về điều kiện giao thoa

• Xác định điều kiện để có giao thoa ánh sáng, tính toán các giá trị phù hợp để thỏa mãn các điều kiện này.
• Áp dụng lý thuyết vào các bài tập liên quan đến giao thoa ánh sáng giữa các nguồn sáng khác nhau.

7.5. Bài tập về giao thoa nhiều sóng ánh sáng

• Giải quyết các bài toán liên quan đến giao thoa của nhiều sóng ánh sáng, phân tích sự chồng chập của các sóng này để xác định vân giao thoa.
• Sử dụng các nguyên lý giao thoa để tính toán các thông số liên quan.

7.6. Bài tập về hiệu ứng Doppler trong giao thoa ánh sáng

• Áp dụng công thức của hiệu ứng Doppler để giải quyết các bài tập liên quan đến sự thay đổi tần số và bước sóng trong hiện tượng giao thoa ánh sáng.
• Phân tích sự thay đổi vị trí của các vân sáng và vân tối khi có hiệu ứng Doppler.

7.7. Bài tập về giao thoa ánh sáng trắng

• Giải quyết các bài tập liên quan đến giao thoa của ánh sáng trắng, phân tích phổ giao thoa thu được trên màn.
• Tính toán vị trí các vân màu khác nhau trong phổ giao thoa ánh sáng trắng.

7.8. Bài tập về giao thoa với ánh sáng đơn sắc

• Giải các bài toán cơ bản về giao thoa ánh sáng đơn sắc, sử dụng các công thức cơ bản để tính toán các thông số liên quan.
• Áp dụng lý thuyết để giải quyết các vấn đề phức tạp hơn về giao thoa ánh sáng đơn sắc.

7.9. Bài tập về giao thoa với nguồn sáng không kết hợp

• Phân tích và giải bài tập về giao thoa của ánh sáng từ các nguồn không kết hợp, xác định các yếu tố ảnh hưởng đến hiện tượng giao thoa trong trường hợp này.
• Sử dụng các nguyên lý cơ bản để dự đoán và tính toán các kết quả giao thoa.

7.10. Bài tập về giao thoa và nguyên lý Huygens

• Áp dụng nguyên lý Huygens để giải quyết các bài toán về giao thoa ánh sáng, phân tích sự tạo thành các vân giao thoa dựa trên nguyên lý này.
• Giải quyết các bài toán phức tạp hơn bằng cách kết hợp nguyên lý Huygens với các nguyên lý khác trong hiện tượng giao thoa ánh sáng.