Chủ đề để khảo sát giao thoa sóng cơ: Để khảo sát giao thoa sóng cơ, bạn cần hiểu rõ các nguyên tắc cơ bản về hiện tượng này, từ cấu trúc thí nghiệm cho đến các ứng dụng thực tiễn. Bài viết này sẽ giúp bạn nắm vững các kiến thức cần thiết để thực hiện và phân tích thí nghiệm giao thoa sóng cơ một cách hiệu quả.
Mục lục
- Khảo Sát Giao Thoa Sóng Cơ Trên Mặt Nước
- Mục Lục Tổng Hợp
- 10 Dạng Bài Tập Giao Thoa Sóng Cơ
- Bài Tập 1: Xác Định Biên Độ Dao Động Tại Một Điểm Trên Mặt Nước
- Bài Tập 2: Tìm Hiệu Đường Đi Sóng Từ Hai Nguồn Kết Hợp
- Bài Tập 3: Tính Chu Kỳ Dao Động Của Một Điểm Trên Mặt Nước
- Bài Tập 4: Xác Định Tần Số Sóng Từ Hai Nguồn Dao Động
- Bài Tập 5: Phân Tích Các Vị Trí Cực Đại Và Cực Tiểu Trong Giao Thoa Sóng
- Bài Tập 6: Tìm Khoảng Cách Giữa Hai Điểm Dao Động Đồng Pha
- Bài Tập 7: Tính Vận Tốc Truyền Sóng Trên Mặt Nước
- Bài Tập 8: Phân Tích Sự Tác Động Của Môi Trường Đến Biên Độ Sóng
- Bài Tập 9: Xác Định Góc Giao Thoa Giữa Hai Sóng
- Bài Tập 10: Tìm Hiệu Số Pha Giữa Hai Sóng Tại Một Điểm Xác Định
Khảo Sát Giao Thoa Sóng Cơ Trên Mặt Nước
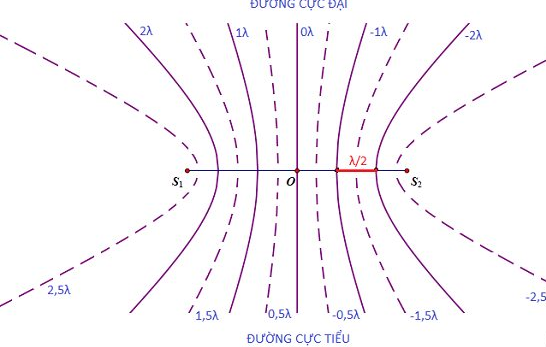
Trong hiện tượng giao thoa sóng cơ, người ta thường sử dụng một thí nghiệm để khảo sát sự giao thoa của hai nguồn sóng cơ. Bố trí thí nghiệm được thực hiện trên mặt nước nằm ngang, với hai nguồn kết hợp \( S_1 \) và \( S_2 \), dao động điều hòa theo phương thẳng đứng và cùng pha. Quá trình này đảm bảo rằng biên độ sóng không thay đổi trong quá trình truyền sóng.
Nguyên Tắc Của Hiện Tượng Giao Thoa Sóng Cơ
- Hai nguồn sóng \( S_1 \) và \( S_2 \) phải là hai nguồn kết hợp, nghĩa là chúng phải dao động cùng pha và có cùng tần số.
- Sóng từ hai nguồn này sẽ gặp nhau và tạo ra các vân giao thoa trên mặt nước.
- Các điểm trên đường trung trực của đoạn \( S_1 S_2 \) sẽ dao động với biên độ cực đại, vì sóng từ hai nguồn đến những điểm này có hiệu đường đi bằng một số nguyên lần bước sóng \( \lambda \).
Hiện Tượng Giao Thoa
Các điểm trên mặt nước sẽ dao động với các biên độ khác nhau tùy thuộc vào vị trí của chúng so với hai nguồn. Cụ thể:
- Những điểm có hiệu đường đi của sóng từ hai nguồn bằng một số lẻ lần nửa bước sóng \( \lambda/2 \) sẽ dao động với biên độ cực tiểu.
- Những điểm có hiệu đường đi bằng một số nguyên lần bước sóng \( \lambda \) sẽ dao động với biên độ cực đại.
Ứng Dụng Thực Tiễn
Thí nghiệm khảo sát giao thoa sóng cơ không chỉ giúp hiểu rõ hơn về nguyên lý giao thoa mà còn là nền tảng để nghiên cứu các hiện tượng sóng phức tạp khác như sóng âm và sóng ánh sáng. Nó cũng giúp minh họa một cách sinh động các khái niệm lý thuyết trong vật lý sóng.
Bảng Tổng Kết Các Đại Lượng
| Đại Lượng | Ký Hiệu | Ý Nghĩa |
| Biên độ dao động cực đại | \( A_{max} \) | Biên độ tại các điểm có hiệu đường đi bằng bội số nguyên lần bước sóng |
| Biên độ dao động cực tiểu | \( A_{min} \) | Biên độ tại các điểm có hiệu đường đi bằng số lẻ lần nửa bước sóng |
| Bước sóng | \( \lambda \) | Khoảng cách giữa hai điểm gần nhau nhất trên mặt nước dao động đồng pha |
Nhờ các thí nghiệm này, các học sinh và nhà nghiên cứu có thể quan sát trực tiếp hiện tượng giao thoa, hiểu rõ hơn về tính chất sóng và cách mà sóng tương tác với nhau trong không gian.

.png)
Mục Lục Tổng Hợp
Khảo sát giao thoa sóng cơ là một chủ đề quan trọng trong vật lý sóng, bao gồm nhiều khía cạnh từ lý thuyết đến ứng dụng thực tiễn. Dưới đây là mục lục tổng hợp chi tiết để giúp bạn nắm vững nội dung này một cách toàn diện.
- Giới Thiệu Về Giao Thoa Sóng Cơ
- Khái niệm và tầm quan trọng của hiện tượng giao thoa sóng cơ.
- Vai trò của giao thoa sóng cơ trong vật lý và đời sống.
- Các Nguyên Tắc Cơ Bản Trong Giao Thoa Sóng Cơ
- Điều kiện để xảy ra giao thoa sóng cơ: tần số, pha, biên độ.
- Sóng kết hợp và nguyên lý hoạt động.
- Giải thích chi tiết về hiện tượng giao thoa.
- Thí Nghiệm Giao Thoa Sóng Cơ Trên Mặt Nước
- Cách bố trí và thực hiện thí nghiệm.
- Phân tích kết quả thí nghiệm giao thoa sóng cơ.
- Những điểm cần lưu ý khi tiến hành thí nghiệm.
- Ứng Dụng Thực Tiễn Của Giao Thoa Sóng Cơ
- Ứng dụng trong công nghệ sóng âm và sóng ánh sáng.
- Tác động của giao thoa sóng cơ trong đời sống hàng ngày.
- Phân Tích Các Yếu Tố Ảnh Hưởng Đến Giao Thoa Sóng Cơ
- Ảnh hưởng của môi trường truyền sóng.
- Biên độ, tần số và khoảng cách giữa các nguồn sóng.
- Các hiện tượng đặc biệt như giao thoa cực đại, cực tiểu.
- Lời Giải Cho Các Bài Tập Giao Thoa Sóng Cơ
- Bài tập 1: Tính hiệu đường đi và phân tích sự giao thoa.
- Bài tập 2: Xác định vị trí cực đại và cực tiểu trên mặt nước.
- Bài tập 3: Phân tích hiện tượng giao thoa trong môi trường khác nhau.
10 Dạng Bài Tập Giao Thoa Sóng Cơ
Khảo sát giao thoa sóng cơ không chỉ giúp hiểu rõ hiện tượng sóng mà còn rèn luyện khả năng phân tích và giải quyết các bài toán phức tạp. Dưới đây là 10 dạng bài tập mẫu điển hình về giao thoa sóng cơ, mỗi bài tập đều được phân tích và hướng dẫn giải chi tiết.
- Bài Tập 1: Tính Hiệu Đường Đi Sóng
Cho hai nguồn sóng kết hợp \(S_1\) và \(S_2\) phát sóng có tần số và pha giống nhau. Xác định hiệu đường đi sóng đến một điểm \(P\) bất kỳ trên mặt nước.
- Bài Tập 2: Xác Định Vị Trí Cực Đại Giao Thoa
Với hai nguồn sóng \(S_1\) và \(S_2\), hãy tính vị trí các điểm cực đại giao thoa trên mặt phẳng.
- Bài Tập 3: Phân Tích Tần Số Sóng Trong Môi Trường Khác Nhau
Xác định tần số của sóng khi chúng truyền qua các môi trường khác nhau và phân tích sự thay đổi của chúng.
- Bài Tập 4: Tìm Vị Trí Cực Tiểu Giao Thoa
Với hai nguồn sóng \(S_1\) và \(S_2\) đặt trên một mặt phẳng, tính toán vị trí các điểm cực tiểu trên mặt nước.
- Bài Tập 5: Xác Định Biên Độ Tại Một Điểm
Cho hai sóng kết hợp, hãy tính biên độ dao động tại một điểm cụ thể trên mặt nước.
- Bài Tập 6: Phân Tích Sự Giao Thoa Khi Sóng Gặp Chướng Ngại Vật
Phân tích hiện tượng giao thoa khi sóng gặp chướng ngại vật và xác định các vị trí cực đại, cực tiểu.
- Bài Tập 7: Xác Định Góc Giao Thoa
Tính toán góc giao thoa giữa hai sóng phát ra từ hai nguồn kết hợp \(S_1\) và \(S_2\).
- Bài Tập 8: Tính Khoảng Cách Giữa Hai Điểm Cực Đại Liên Tiếp
Cho hai nguồn sóng \(S_1\) và \(S_2\), tính khoảng cách giữa hai điểm cực đại liên tiếp trên mặt phẳng.
- Bài Tập 9: Phân Tích Ảnh Hưởng Của Biên Độ Sóng
Xác định ảnh hưởng của sự thay đổi biên độ sóng đến hiện tượng giao thoa.
- Bài Tập 10: Xác Định Tần Số Dao Động Tại Một Điểm
Tính toán tần số dao động của một điểm bất kỳ trên mặt nước khi có hiện tượng giao thoa sóng cơ xảy ra.

Bài Tập 1: Xác Định Biên Độ Dao Động Tại Một Điểm Trên Mặt Nước
Trong bài tập này, chúng ta sẽ xác định biên độ dao động của sóng tại một điểm \(P\) trên mặt nước, khi có hai nguồn sóng kết hợp \(S_1\) và \(S_2\) phát sóng. Để giải quyết vấn đề này, ta cần làm theo các bước sau:
- Xác Định Khoảng Cách Từ Các Nguồn Đến Điểm P
Giả sử khoảng cách từ điểm \(P\) đến hai nguồn sóng là \(d_1\) và \(d_2\). Bạn có thể xác định các giá trị này bằng cách đo trực tiếp hoặc thông qua các thông số đã cho trước trong đề bài.
- Tính Hiệu Đường Đi Sóng \(\Delta d\)
Hiệu đường đi sóng \(\Delta d\) được tính bằng công thức:
\[ \Delta d = |d_1 - d_2| \]Hiệu đường đi sóng này quyết định tính chất của giao thoa tại điểm \(P\).
- Xác Định Pha Chênh Lệch \(\Delta \phi\)
Pha chênh lệch \(\Delta \phi\) giữa hai sóng tại điểm \(P\) được tính theo công thức:
\[ \Delta \phi = \frac{2\pi \Delta d}{\lambda} \]Trong đó, \(\lambda\) là bước sóng của sóng phát ra từ các nguồn \(S_1\) và \(S_2\).
- Tính Biên Độ Tổng Hợp Tại Điểm P
Biên độ dao động tổng hợp \(A_P\) tại điểm \(P\) được tính theo công thức:
\[ A_P = 2A_0 \cos \left(\frac{\Delta \phi}{2}\right) \]Trong đó, \(A_0\) là biên độ của sóng từ mỗi nguồn.
- Kết Luận Về Biên Độ Tại Điểm P
Thông qua các bước trên, ta xác định được biên độ dao động tại điểm \(P\) trên mặt nước. Nếu \(\Delta \phi\) là một bội số của \(2\pi\), thì biên độ tổng hợp đạt cực đại, ngược lại, nếu \(\Delta \phi\) là bội số của \(\pi\), biên độ sẽ đạt cực tiểu.
XEM THÊM:
Bài Tập 2: Tìm Hiệu Đường Đi Sóng Từ Hai Nguồn Kết Hợp
Bài tập này hướng dẫn cách tính toán hiệu đường đi sóng giữa hai nguồn sóng kết hợp \(S_1\) và \(S_2\). Hiệu đường đi sóng \(\Delta d\) là một yếu tố quan trọng trong việc xác định các điểm cực đại và cực tiểu của giao thoa sóng. Dưới đây là các bước chi tiết để giải quyết bài toán này:
- Xác Định Tọa Độ Các Nguồn Và Điểm Quan Sát
Giả sử tọa độ của các nguồn \(S_1\) và \(S_2\) lần lượt là \((x_1, y_1)\) và \((x_2, y_2)\). Điểm quan sát \(P\) có tọa độ \((x_P, y_P)\).
- Tính Khoảng Cách Từ Các Nguồn Đến Điểm Quan Sát
Khoảng cách từ điểm \(P\) đến các nguồn \(S_1\) và \(S_2\) được tính theo công thức:
\[ d_1 = \sqrt{(x_P - x_1)^2 + (y_P - y_1)^2} \] \[ d_2 = \sqrt{(x_P - x_2)^2 + (y_P - y_2)^2} \] - Tính Hiệu Đường Đi Sóng \(\Delta d\)
Hiệu đường đi sóng \(\Delta d\) giữa hai nguồn được xác định bằng:
\[ \Delta d = |d_1 - d_2| \]Hiệu đường đi sóng này sẽ ảnh hưởng trực tiếp đến hiện tượng giao thoa tại điểm \(P\).
- Phân Tích Kết Quả
Nếu hiệu đường đi sóng \(\Delta d\) là bội số của bước sóng \(\lambda\), tại điểm \(P\) sẽ xảy ra hiện tượng giao thoa cực đại. Nếu \(\Delta d\) là bội số của \(\lambda/2\), tại điểm đó sẽ xảy ra hiện tượng giao thoa cực tiểu.

Bài Tập 3: Tính Chu Kỳ Dao Động Của Một Điểm Trên Mặt Nước
Trong bài tập này, chúng ta sẽ tính chu kỳ dao động của một điểm trên mặt nước khi xảy ra hiện tượng giao thoa sóng cơ. Để tính toán, chúng ta cần hiểu rõ các thông số cơ bản như tần số của sóng, biên độ dao động và khoảng cách giữa các nguồn sóng.
-
Xác định tần số của sóng: Tần số sóng \( f \) có thể được tính bằng công thức:
\[ f = \frac{1}{T} \]
trong đó, \( T \) là chu kỳ dao động mà chúng ta cần xác định.
-
Biểu thức chu kỳ dao động: Chu kỳ dao động của điểm trên mặt nước sẽ phụ thuộc vào tần số sóng theo công thức:
\[ T = \frac{1}{f} \]
Trong đó:
- \( T \): Chu kỳ dao động.
- \( f \): Tần số dao động.
-
Tính toán cụ thể: Sau khi xác định được tần số sóng từ các thông số cho trước, chúng ta áp dụng công thức trên để tính chu kỳ dao động \( T \).
Ví dụ, nếu tần số \( f = 2 \, \text{Hz} \), thì chu kỳ dao động sẽ là:
\[ T = \frac{1}{2} = 0.5 \, \text{giây} \]
Như vậy, bằng cách áp dụng các công thức toán học đơn giản, chúng ta có thể dễ dàng tính được chu kỳ dao động của một điểm trên mặt nước trong điều kiện giao thoa sóng cơ.
Bài Tập 4: Xác Định Tần Số Sóng Từ Hai Nguồn Dao Động
Trong bài tập này, chúng ta sẽ xác định tần số của sóng cơ học xuất phát từ hai nguồn dao động đồng pha và cùng biên độ. Bài tập sẽ hướng dẫn từng bước tính toán tần số dựa trên các thông số đã cho như vận tốc sóng, khoảng cách giữa hai nguồn và điểm khảo sát.
- Xác định các thông số đầu vào: vận tốc sóng \(v\), khoảng cách giữa hai nguồn \(d\), và khoảng cách từ điểm khảo sát đến hai nguồn.
- Tính toán tần số sóng \(f\) dựa trên công thức \(f = \frac{v}{\lambda}\), trong đó \(\lambda\) là bước sóng.
- Sử dụng dữ liệu đã tính để đưa ra kết quả cuối cùng cho tần số sóng \(f\).
.png)
Bài Tập 5: Phân Tích Các Vị Trí Cực Đại Và Cực Tiểu Trong Giao Thoa Sóng
Trong bài tập này, chúng ta sẽ tiến hành phân tích và xác định các vị trí cực đại và cực tiểu trong hiện tượng giao thoa sóng cơ học. Để thực hiện bài tập, bạn cần tuân theo các bước sau đây:
- Xác định các nguồn sóng: Xác định tọa độ và các thông số cơ bản của hai nguồn sóng \(S_1\) và \(S_2\).
- Xác định điều kiện giao thoa: Điều kiện để có cực đại giao thoa là khi hiệu đường đi của sóng từ hai nguồn tới một điểm bất kỳ thỏa mãn \(\Delta d = k\lambda\), với \(k\) là số nguyên. Để có cực tiểu, điều kiện là \(\Delta d = (k + \frac{1}{2})\lambda\).
- Tính toán vị trí cực đại và cực tiểu: Sử dụng các điều kiện đã xác định ở trên để tìm ra các vị trí trên mặt nước nơi xảy ra cực đại và cực tiểu.
- Phân tích kết quả: Đánh giá sự phân bố của các cực đại và cực tiểu trong không gian, từ đó rút ra các nhận xét về tính chất giao thoa sóng.
Việc xác định các vị trí cực đại và cực tiểu không chỉ giúp hiểu rõ hơn về hiện tượng giao thoa sóng cơ mà còn giúp áp dụng vào các bài toán thực tiễn khác liên quan đến sóng cơ học.

Bài Tập 6: Tìm Khoảng Cách Giữa Hai Điểm Dao Động Đồng Pha
Để tìm khoảng cách giữa hai điểm dao động đồng pha trên mặt nước từ hai nguồn sóng cơ học kết hợp, ta cần xét điều kiện giao thoa của hai nguồn sóng. Hai điểm trên mặt nước sẽ dao động đồng pha khi hiệu đường đi của sóng từ hai nguồn đến các điểm đó bằng một bội số nguyên của bước sóng.
Giả sử hai nguồn sóng đồng pha \(S_1\) và \(S_2\) có khoảng cách \(d\), vận tốc truyền sóng \(v\) và tần số dao động \(f\). Bước sóng được tính theo công thức:
\[
\lambda = \frac{v}{f}
\]
Khoảng cách giữa hai điểm dao động đồng pha gần nhất là:
\[
\Delta x = k\lambda
\]
Với \(k\) là số nguyên dương và \(k \geq 1\). Để xác định khoảng cách, ta cần biết chính xác bước sóng và vị trí các điểm dao động.
Ví dụ: Giả sử bước sóng của sóng là \(2\) cm, hai điểm gần nhất dao động đồng pha cách nhau \(2\) cm, tức là \(\Delta x = 2\) cm.
Trong thực tế, để tìm khoảng cách giữa các điểm dao động đồng pha, ta cần tiến hành đo đạc và tính toán dựa trên công thức trên, từ đó xác định được vị trí và khoảng cách các điểm dao động đồng pha với độ chính xác cao.
Bài Tập 7: Tính Vận Tốc Truyền Sóng Trên Mặt Nước
Để khảo sát giao thoa sóng cơ và tính vận tốc truyền sóng trên mặt nước, chúng ta có thể sử dụng phương pháp bố trí hai nguồn kết hợp dao động điều hòa. Phương pháp này cho phép xác định các điểm cực đại và cực tiểu giao thoa trên mặt nước, từ đó tính toán các thông số liên quan đến sóng.
Giả sử:
- Hai nguồn dao động tại hai điểm S1 và S2 trên mặt nước cách nhau khoảng cách \(d\).
- Các nguồn dao động cùng pha và có tần số \(f\).
Bước 1: Xác định khoảng cách giữa hai cực đại hoặc hai cực tiểu liên tiếp.
Theo lý thuyết giao thoa, khoảng cách giữa hai điểm cực đại hoặc hai điểm cực tiểu liên tiếp trên đường trung trực là một nửa bước sóng, tức là \( \Delta x = \dfrac{\lambda}{2} \).
Bước 2: Tính bước sóng \( \lambda \).
Sử dụng công thức:
Trong đó:
- \( v \) là vận tốc truyền sóng.
- \( f \) là tần số dao động của nguồn.
Bước 3: Tính vận tốc truyền sóng \( v \).
Vận tốc truyền sóng có thể được tính thông qua việc đo khoảng cách giữa hai điểm cực đại hoặc cực tiểu liên tiếp và tần số của nguồn dao động:
Đây là công thức cơ bản để xác định vận tốc truyền sóng trên mặt nước thông qua khảo sát giao thoa sóng cơ.

Bài Tập 8: Phân Tích Sự Tác Động Của Môi Trường Đến Biên Độ Sóng
Trong hiện tượng giao thoa sóng cơ học, biên độ của sóng tại các điểm trên mặt nước chịu sự ảnh hưởng mạnh mẽ từ môi trường truyền sóng. Để phân tích sự tác động này, chúng ta cần xem xét một số yếu tố chính như độ sâu của nước, tạp chất trong nước, và tính đồng nhất của môi trường.
- Độ sâu của nước: Độ sâu ảnh hưởng trực tiếp đến vận tốc truyền sóng và biên độ sóng. Khi độ sâu thay đổi, biên độ sóng sẽ giảm hoặc tăng tùy thuộc vào sự thay đổi đó. Trong vùng nước nông, sóng có biên độ lớn hơn do năng lượng sóng tập trung.
- Tạp chất trong nước: Các hạt cát, bùn, hay các tạp chất khác làm giảm biên độ sóng khi truyền qua do một phần năng lượng sóng bị hấp thụ hoặc tán xạ.
- Tính đồng nhất của môi trường: Nếu môi trường không đồng nhất (có các lớp nước với nhiệt độ hoặc độ mặn khác nhau), sự phản xạ và khúc xạ của sóng tại các ranh giới này sẽ làm thay đổi biên độ sóng.
Phương trình mô tả biên độ sóng tại điểm M có dạng:
Trong đó:
- \(A_M\) là biên độ sóng tại điểm M.
- \(\lambda\) là bước sóng.
- \(\Delta \varphi\) là độ lệch pha giữa hai nguồn sóng.
- \(d_2\) và \(d_1\) là khoảng cách từ hai nguồn sóng đến điểm M.
Qua phương trình trên, ta thấy biên độ sóng tại điểm M không chỉ phụ thuộc vào độ lệch pha giữa hai nguồn sóng mà còn chịu ảnh hưởng từ sự thay đổi của môi trường truyền sóng. Để khảo sát chi tiết, có thể thực hiện các thí nghiệm với các biến đổi khác nhau của môi trường, từ đó quan sát sự thay đổi biên độ và đưa ra các kết luận chính xác.
Bài Tập 9: Xác Định Góc Giao Thoa Giữa Hai Sóng
Để giải quyết bài tập xác định góc giao thoa giữa hai sóng cơ học, ta cần xem xét các yếu tố chính như vị trí của hai nguồn sóng, phương trình sóng, và sự chênh lệch pha giữa các sóng tại một điểm xác định.
-
Bước 1: Xác định vị trí của hai nguồn sóng.
Giả sử hai nguồn sóng \(S_1\) và \(S_2\) được đặt tại các vị trí khác nhau trên mặt nước. Hai nguồn này dao động điều hòa theo phương thẳng đứng và có tần số giống nhau.
-
Bước 2: Viết phương trình sóng từ hai nguồn.
Phương trình sóng từ \(S_1\) và \(S_2\) lần lượt là:
\[
u_1 = A \cos (\omega t - kx_1)
\]
\[
u_2 = A \cos (\omega t - kx_2)
\] -
Bước 3: Xác định vị trí giao thoa cực đại và cực tiểu.
Sóng giao thoa cực đại xảy ra khi pha chênh lệch giữa hai sóng thỏa mãn:
\[
\Delta \varphi = 2n\pi
\]Sóng giao thoa cực tiểu xảy ra khi pha chênh lệch giữa hai sóng thỏa mãn:
\[
\Delta \varphi = (2n+1)\pi
\] -
Bước 4: Tính góc giao thoa giữa hai sóng.
Góc giao thoa \(\theta\) được xác định từ việc tính toán giữa các vị trí mà sóng giao thoa cực đại hoặc cực tiểu. Góc này phụ thuộc vào khoảng cách giữa hai nguồn sóng và bước sóng \(\lambda\).
Với các bước trên, bạn có thể xác định được góc giao thoa giữa hai sóng trong điều kiện lý tưởng, giúp hiểu rõ hơn về hiện tượng giao thoa sóng cơ học.
Bài Tập 10: Tìm Hiệu Số Pha Giữa Hai Sóng Tại Một Điểm Xác Định
Để tìm hiệu số pha giữa hai sóng tại một điểm xác định, ta cần xem xét các yếu tố như khoảng cách từ điểm đó đến hai nguồn sóng, bước sóng và tần số của sóng. Bài tập này yêu cầu tính toán cẩn thận và chính xác, vì sự thay đổi nhỏ trong các thông số có thể dẫn đến kết quả khác nhau.
- Xác định vị trí của điểm M và khoảng cách từ điểm đó đến hai nguồn \(d_1\) và \(d_2\).
- Tính toán độ lệch đường đi \(\Delta d = |d_2 - d_1|\).
- Sử dụng công thức tính hiệu số pha: \[ \Delta \varphi = \frac{2\pi \Delta d}{\lambda} \] trong đó \( \lambda \) là bước sóng.
- Xác định kết quả cuối cùng dựa trên giá trị của \( \Delta \varphi \):
- Nếu \( \Delta \varphi = 0, 2\pi, 4\pi, \dots \) thì hai sóng cùng pha.
- Nếu \( \Delta \varphi = \pi, 3\pi, 5\pi, \dots \) thì hai sóng ngược pha.
- Giá trị khác giữa 0 và \(\pi\) biểu thị hai sóng có độ lệch pha khác.
Bài tập này giúp làm rõ mối quan hệ giữa vị trí, khoảng cách, và hiệu số pha trong quá trình giao thoa sóng cơ. Kết quả thu được từ việc tính toán hiệu số pha không chỉ mang tính lý thuyết mà còn có ứng dụng thực tiễn trong các thí nghiệm giao thoa sóng.