Chủ đề bài 25 giao thoa ánh sáng: Bài 25 về giao thoa ánh sáng là một trong những chủ đề quan trọng trong chương trình Vật Lý lớp 12. Bài viết này sẽ giúp bạn hiểu rõ hơn về hiện tượng nhiễu xạ và giao thoa ánh sáng, các thí nghiệm kinh điển, và ứng dụng thực tiễn của chúng. Cùng khám phá các khái niệm quan trọng và bài tập thực hành để nắm vững kiến thức về giao thoa ánh sáng.
Mục lục
- Bài 25: Giao Thoa Ánh Sáng
- Mục Lục Tổng Hợp
- 10 Dạng Bài Tập Về Giao Thoa Ánh Sáng
- Bài Tập 1: Tính Khoảng Vân Trong Thí Nghiệm Y-âng
- Bài Tập 2: Tính Hiệu Số Đường Đi Của Hai Sóng Kết Hợp
- Bài Tập 3: Xác Định Vị Trí Các Vân Sáng và Tối
- Bài Tập 4: Tính Bước Sóng Ánh Sáng Từ Kết Quả Thí Nghiệm
- Bài Tập 5: Xác Định Màu Sắc Tại Các Vị Trí Cụ Thể
- Bài Tập 6: Ứng Dụng Giao Thoa Trong Đo Độ Dày Tấm Mỏng
- Bài Tập 7: Tính Khoảng Vân Khi Thay Đổi Khoảng Cách Giữa Hai Khe
- Bài Tập 8: Xác Định Số Vân Sáng Tối Trên Màn
- Bài Tập 9: Tính Toán Khi Có Sự Thay Đổi Bước Sóng
- Bài Tập 10: Các Dạng Bài Tập Kết Hợp Khác
Bài 25: Giao Thoa Ánh Sáng
Trong bài 25 của chương trình Vật Lý lớp 12, hiện tượng giao thoa ánh sáng được nghiên cứu nhằm giúp học sinh hiểu rõ về các khái niệm cơ bản như hiện tượng nhiễu xạ, giao thoa ánh sáng, và cách ánh sáng có tính chất sóng.
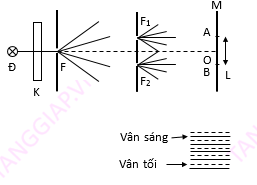
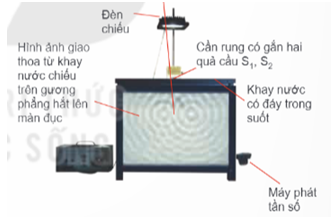
I. Hiện Tượng Nhiễu Xạ Ánh Sáng
Hiện tượng nhiễu xạ ánh sáng xảy ra khi ánh sáng truyền lệch hướng do gặp vật cản, cho thấy ánh sáng có tính chất sóng. Mỗi loại ánh sáng đơn sắc có bước sóng hoặc tần số xác định trong chân không.
II. Hiện Tượng Giao Thoa Ánh Sáng
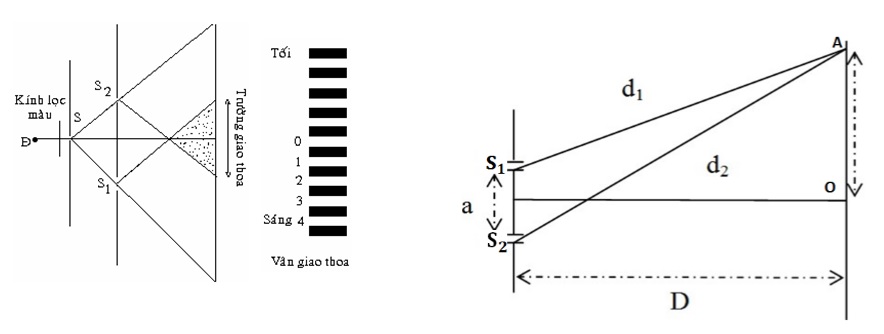
Thí nghiệm Y-âng (Young) chứng minh rằng ánh sáng có thể giao thoa, nghĩa là hai chùm sáng từ các nguồn kết hợp (có cùng bước sóng và hiệu số pha không đổi) có thể tạo ra các vân giao thoa trên màn.
Công thức tính khoảng vân \(i\):
Trong đó:
- \(\lambda\): Bước sóng ánh sáng
- a: Khoảng cách giữa hai khe
- D: Khoảng cách từ hai khe đến màn quan sát
III. Bước Sóng Ánh Sáng và Màu Sắc
Các ánh sáng đơn sắc có bước sóng trong khoảng từ 380 nm đến 760 nm sẽ tạo ra các màu sắc khả kiến. Ánh sáng trắng là hỗn hợp của nhiều bước sóng khác nhau, giúp mắt phân biệt màu sắc.
Bảng bước sóng ánh sáng nhìn thấy:
| Màu | Bước sóng (nm) |
| Tím | 380 - 450 |
| Lam | 450 - 495 |
| Lục | 495 - 570 |
| Vàng | 570 - 590 |
| Cam | 590 - 620 |
| Đỏ | 620 - 760 |

.png)
Mục Lục Tổng Hợp
Dưới đây là danh sách các nội dung chính được trình bày trong bài học "Bài 25 Giao Thoa Ánh Sáng". Mỗi phần sẽ giải thích chi tiết các khái niệm cơ bản và nâng cao liên quan đến hiện tượng giao thoa ánh sáng.
- 1. Giới Thiệu Về Hiện Tượng Giao Thoa Ánh Sáng
- 2. Thí Nghiệm Y-âng: Nguyên Lý và Tiến Hành
- 3. Công Thức Tính Khoảng Vân: \[i = \dfrac{\lambda D}{a}\]
- 4. Các Yếu Tố Ảnh Hưởng Đến Giao Thoa Ánh Sáng
- 5. Ứng Dụng Của Hiện Tượng Giao Thoa Trong Thực Tiễn
- 6. Các Dạng Bài Tập Cơ Bản và Nâng Cao
- 7. Tổng Kết và Luyện Tập
10 Dạng Bài Tập Về Giao Thoa Ánh Sáng
Dưới đây là danh sách 10 dạng bài tập về hiện tượng giao thoa ánh sáng, giúp học sinh nắm vững kiến thức lý thuyết và vận dụng vào các bài toán thực tế.
- Bài Tập 1: Tính khoảng vân \[i = \dfrac{\lambda D}{a}\] trong thí nghiệm Y-âng.
- Bài Tập 2: Xác định vị trí các vân sáng, vân tối trên màn hình.
- Bài Tập 3: Tính bước sóng \(\lambda\) của ánh sáng dựa trên kết quả thí nghiệm.
- Bài Tập 4: Xác định hiệu số đường đi của hai sóng kết hợp.
- Bài Tập 5: Tính toán khi thay đổi khoảng cách giữa hai khe.
- Bài Tập 6: Ứng dụng giao thoa ánh sáng để đo độ dày tấm mỏng.
- Bài Tập 7: Xác định số vân sáng, vân tối xuất hiện trên màn hình.
- Bài Tập 8: Bài toán về sự thay đổi màu sắc tại các vị trí cụ thể.
- Bài Tập 9: Tính khoảng vân khi bước sóng ánh sáng thay đổi.
- Bài Tập 10: Các bài tập kết hợp khác về giao thoa và nhiễu xạ ánh sáng.

Bài Tập 1: Tính Khoảng Vân Trong Thí Nghiệm Y-âng
Trong bài tập này, chúng ta sẽ tính toán khoảng vân \(i\) trong thí nghiệm Y-âng, một hiện tượng quan trọng trong giao thoa ánh sáng. Khoảng vân là khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp trên màn giao thoa.
- Bước 1: Xác định các giá trị ban đầu: bước sóng ánh sáng \(\lambda\), khoảng cách giữa hai khe \(a\), và khoảng cách từ khe đến màn \(D\).
- Bước 2: Sử dụng công thức tính khoảng vân: \[i = \dfrac{\lambda D}{a}\].
- Bước 3: Thay các giá trị vào công thức và thực hiện phép tính để tìm khoảng vân \(i\).
- Bước 4: Kiểm tra và xác nhận kết quả.

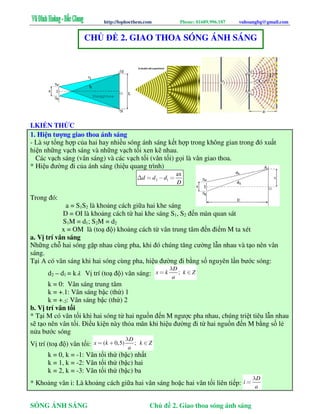
Bài Tập 2: Tính Hiệu Số Đường Đi Của Hai Sóng Kết Hợp
Trong bài tập này, chúng ta sẽ tính toán hiệu số đường đi \(\Delta d\) của hai sóng kết hợp trong thí nghiệm giao thoa ánh sáng. Hiệu số này quyết định vị trí của các vân sáng và vân tối trên màn.
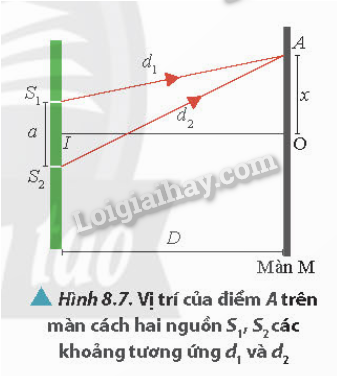
- Bước 1: Xác định vị trí của hai nguồn sóng kết hợp và điểm khảo sát trên màn.
- Bước 2: Tính toán khoảng cách từ từng nguồn đến điểm khảo sát, gọi là \(d_1\) và \(d_2\).
- Bước 3: Tính hiệu số đường đi: \[\Delta d = d_2 - d_1\].
- Bước 4: Đánh giá kết quả dựa trên giá trị của \(\Delta d\).

Bài Tập 3: Xác Định Vị Trí Các Vân Sáng và Tối
Bài tập này giúp bạn xác định chính xác vị trí các vân sáng và vân tối trên màn trong thí nghiệm giao thoa ánh sáng, dựa trên khoảng cách giữa hai nguồn sáng và bước sóng của ánh sáng.
- Bước 1: Xác định khoảng cách giữa hai khe \(a\) và khoảng cách từ khe đến màn \(D\).
- Bước 2: Tính khoảng vân \(i = \frac{\lambda D}{a}\).
- Bước 3: Vị trí các vân sáng được xác định bởi công thức: \[x_k = k\cdot i\], với \(k\) là số nguyên.
- Bước 4: Vị trí các vân tối được xác định bởi công thức: \[x_{k'} = \left(k + \frac{1}{2}\right)\cdot i\], với \(k\) là số nguyên.
XEM THÊM:
Bài Tập 4: Tính Bước Sóng Ánh Sáng Từ Kết Quả Thí Nghiệm
Bài tập này giúp bạn tính toán bước sóng ánh sáng dựa trên các kết quả thu được từ thí nghiệm giao thoa ánh sáng. Bạn sẽ sử dụng công thức và dữ liệu thực nghiệm để đưa ra giá trị chính xác của bước sóng.
- Bước 1: Xác định khoảng cách giữa hai khe \(a\) và khoảng cách từ khe đến màn \(D\).
- Bước 2: Đo khoảng cách giữa các vân sáng liên tiếp trên màn \(i\).
- Bước 3: Tính bước sóng ánh sáng bằng công thức: \[\lambda = \frac{i \cdot a}{D}\].

Bài Tập 5: Xác Định Màu Sắc Tại Các Vị Trí Cụ Thể
Để xác định màu sắc tại các vị trí cụ thể trong hiện tượng giao thoa ánh sáng, ta cần tính toán bước sóng tương ứng với các vân sáng và tối trên màn.
- Bước 1: Xác định bước sóng của ánh sáng sử dụng trong thí nghiệm. Giả sử bước sóng của ánh sáng đơn sắc là \(\lambda\).
- Bước 2: Tính khoảng vân \(i\) dựa trên công thức:
\[
i = \frac{\lambda D}{a}
\]
Trong đó:
- \(\lambda\) là bước sóng của ánh sáng.
- \(D\) là khoảng cách từ hai khe đến màn quan sát.
- \(a\) là khoảng cách giữa hai khe sáng.
- Bước 3: Xác định vị trí vân sáng, tối tại vị trí cụ thể \(x\) từ công thức: \[ x = m \cdot i \] Với \(m\) là bậc của vân sáng. Các vị trí vân sáng tương ứng với \(m = 0, 1, 2, \dots\), còn các vị trí vân tối là \(m = \frac{1}{2}, \frac{3}{2}, \frac{5}{2}, \dots\).
- Bước 4: Tính toán màu sắc dựa trên bước sóng tương ứng:
- Nếu bước sóng thuộc khoảng từ 380 nm đến 450 nm, màu sắc sẽ là tím.
- Nếu bước sóng thuộc khoảng từ 450 nm đến 495 nm, màu sắc sẽ là xanh lam.
- Nếu bước sóng thuộc khoảng từ 495 nm đến 570 nm, màu sắc sẽ là xanh lá.
- Nếu bước sóng thuộc khoảng từ 570 nm đến 590 nm, màu sắc sẽ là vàng.
- Nếu bước sóng thuộc khoảng từ 590 nm đến 620 nm, màu sắc sẽ là cam.
- Nếu bước sóng thuộc khoảng từ 620 nm đến 750 nm, màu sắc sẽ là đỏ.
- Bước 5: Ghi nhận màu sắc tại vị trí cụ thể cần tính toán và so sánh với kết quả thí nghiệm để kiểm tra độ chính xác.
Bằng cách thực hiện các bước trên, ta có thể xác định chính xác màu sắc tại các vị trí cụ thể trên màn giao thoa, giúp làm rõ hiện tượng giao thoa ánh sáng trong thí nghiệm Y-âng.

Bài Tập 6: Ứng Dụng Giao Thoa Trong Đo Độ Dày Tấm Mỏng
Trong bài tập này, chúng ta sẽ tìm hiểu về cách ứng dụng hiện tượng giao thoa ánh sáng để đo độ dày của một tấm mỏng. Phương pháp này dựa trên việc quan sát các vân giao thoa khi ánh sáng đơn sắc truyền qua tấm mỏng.
Nguyên lý: Khi ánh sáng chiếu vào một tấm mỏng, một phần ánh sáng bị phản xạ tại mặt trên của tấm, phần còn lại truyền qua tấm và bị phản xạ tại mặt dưới. Hai chùm ánh sáng này giao thoa với nhau, tạo thành các vân sáng và tối trên màn quan sát.
Biểu thức của vân giao thoa:
Giả sử \( t \) là độ dày của tấm mỏng, \( n \) là chiết suất của tấm, và \( \lambda \) là bước sóng của ánh sáng, thì điều kiện giao thoa tăng cường (vân sáng) và giao thoa triệt tiêu (vân tối) được cho bởi:
- Vân sáng: \[ 2nt = m\lambda \]
- Vân tối: \[ 2nt = (m + \frac{1}{2})\lambda \]
Ở đây, \( m \) là số nguyên (m = 0, 1, 2,...).
Quy trình thực hiện:
- Chuẩn bị: Một tấm mỏng cần đo, một nguồn sáng đơn sắc có bước sóng \( \lambda \), và một màn quan sát.
- Thực hiện:
- Chiếu ánh sáng đơn sắc vuông góc với tấm mỏng.
- Quan sát và đếm số vân sáng và tối xuất hiện trên màn.
- Tính toán:
- Đo khoảng cách giữa hai vân sáng liên tiếp (khoảng vân) \( x \).
- Áp dụng công thức: \[ t = \frac{m\lambda}{2n} \] để tính độ dày \( t \) của tấm mỏng, trong đó \( m \) là số vân sáng đếm được.
Phương pháp này không chỉ đơn giản mà còn mang lại độ chính xác cao trong việc xác định độ dày của các tấm mỏng trong các ứng dụng thực tiễn.
Bài Tập 7: Tính Khoảng Vân Khi Thay Đổi Khoảng Cách Giữa Hai Khe
Trong hiện tượng giao thoa ánh sáng, khoảng vân \(i\) được tính theo công thức:
Trong đó:
- \(\lambda\) là bước sóng của ánh sáng (m).
- \(D\) là khoảng cách từ hai khe đến màn quan sát (m).
- \(a\) là khoảng cách giữa hai khe (m).
Khi thay đổi khoảng cách giữa hai khe, giá trị của khoảng vân \(i\) cũng thay đổi tương ứng. Dưới đây là các bước cụ thể để tính khoảng vân khi thay đổi khoảng cách giữa hai khe:
- Giả sử khoảng cách giữa hai khe ban đầu là \(a_1\), và khoảng vân tương ứng là \(i_1\). Công thức tính khoảng vân là:
- \[ i_1 = \frac{\lambda D}{a_1} \]
- Thay đổi khoảng cách giữa hai khe từ \(a_1\) thành \(a_2\). Khi đó, khoảng vân mới \(i_2\) sẽ được tính theo công thức:
- \[ i_2 = \frac{\lambda D}{a_2} \]
- Tỷ lệ giữa khoảng vân cũ và mới là:
- \[ \frac{i_1}{i_2} = \frac{a_2}{a_1} \]
- Vì vậy, nếu biết giá trị khoảng vân ban đầu \(i_1\) và khoảng cách giữa hai khe \(a_1\), ta có thể tính khoảng vân mới \(i_2\) khi thay đổi khoảng cách giữa hai khe thành \(a_2\) bằng công thức:
- \[ i_2 = i_1 \times \frac{a_1}{a_2} \]
Ví dụ: Giả sử khoảng cách giữa hai khe ban đầu là \(a_1 = 0,5 \, mm\) và khoảng vân tương ứng là \(i_1 = 0,1 \, mm\). Nếu khoảng cách giữa hai khe được thay đổi thành \(a_2 = 0,25 \, mm\), thì khoảng vân mới \(i_2\) sẽ là:
\[
i_2 = 0,1 \, mm \times \frac{0,5 \, mm}{0,25 \, mm} = 0,2 \, mm
\]
Như vậy, khi khoảng cách giữa hai khe giảm đi một nửa, khoảng vân sẽ tăng gấp đôi.

Bài Tập 8: Xác Định Số Vân Sáng Tối Trên Màn
Trong thí nghiệm giao thoa ánh sáng của Y-âng, việc xác định số vân sáng và vân tối trên màn là một phần quan trọng để hiểu rõ hiện tượng giao thoa. Dưới đây là các bước cơ bản để tính toán:
Xác định vị trí của các vân sáng:
Vân sáng xuất hiện khi hiệu đường đi của hai sóng bằng một bội số nguyên lần bước sóng. Công thức xác định vị trí vân sáng trên màn là:
\[
x_k = k\frac{\lambda D}{a}
\]
với:
- \(x_k\) là vị trí của vân sáng thứ \(k\) trên màn.
- \(\lambda\) là bước sóng của ánh sáng.
- \(D\) là khoảng cách từ hai khe đến màn.
- \(a\) là khoảng cách giữa hai khe sáng.
- \(k\) là bậc của vân sáng (k = 0, ±1, ±2,...).
Xác định vị trí của các vân tối:
Vân tối xuất hiện khi hiệu đường đi của hai sóng bằng một bội số lẻ của nửa bước sóng. Công thức xác định vị trí vân tối trên màn là:
\[
x_t = \left(k + \frac{1}{2}\right)\frac{\lambda D}{a}
\]
với:
- \(x_t\) là vị trí của vân tối.
- \(k\) là bậc của vân tối (k = 0, ±1, ±2,...).
Số lượng vân sáng và vân tối trên màn:
Để tính tổng số vân sáng và vân tối xuất hiện trên màn, chúng ta cần xác định giới hạn của màn và tính toán dựa trên các vị trí \(x_k\) và \(x_t\).
Ví dụ, nếu màn quan sát có chiều rộng \(L\) từ \(-x\) đến \(x\), số vân sáng có thể được xác định bằng cách đếm số giá trị nguyên của \(k\) sao cho vị trí của vân sáng nằm trong phạm vi của màn:
\[
-x \leq x_k \leq x
\]Tương tự, số vân tối được xác định bằng cách đếm số giá trị nguyên của \(k + \frac{1}{2}\) sao cho vị trí của vân tối nằm trong phạm vi của màn.
Với các bước trên, bạn có thể dễ dàng xác định được số lượng vân sáng và vân tối trên màn khi thực hiện thí nghiệm giao thoa ánh sáng. Hãy luôn lưu ý đến các yếu tố như bước sóng, khoảng cách giữa các khe, và khoảng cách từ khe đến màn để có kết quả chính xác nhất.
Bài Tập 9: Tính Toán Khi Có Sự Thay Đổi Bước Sóng
Khi thực hiện các thí nghiệm giao thoa ánh sáng, việc thay đổi bước sóng của ánh sáng sẽ ảnh hưởng trực tiếp đến kết quả giao thoa. Trong bài tập này, chúng ta sẽ tính toán số vân sáng và vân tối khi có sự thay đổi bước sóng.
Bước 1: Xác định các tham số ban đầu.
- Khoảng cách giữa hai khe: \(a\)
- Khoảng cách từ hai khe đến màn: \(D\)
- Bước sóng ban đầu của ánh sáng: \(\lambda_1\)
Bước 2: Tính khoảng vân giao thoa \(i_1\) với bước sóng ban đầu:
\[
i_1 = \frac{\lambda_1 \cdot D}{a}
\]
Bước 3: Khi thay đổi bước sóng từ \(\lambda_1\) sang \(\lambda_2\), khoảng vân giao thoa mới \(i_2\) được tính theo công thức:
\[
i_2 = \frac{\lambda_2 \cdot D}{a}
\]
Bước 4: Xác định số vân sáng và vân tối trên màn.
Số vân sáng có thể tính toán dựa trên sự chênh lệch giữa hai khoảng vân giao thoa \(i_1\) và \(i_2\). Nếu \(i_2\) lớn hơn \(i_1\), số vân sáng sẽ tăng lên. Ngược lại, nếu \(i_2\) nhỏ hơn \(i_1\), số vân sáng sẽ giảm đi. Công thức xác định số vân sáng có thể là:
\[
\text{Số vân sáng} = \frac{\text{khoảng vân mới}}{\text{khoảng vân cũ}} \times \text{số vân ban đầu}
\]
Như vậy, việc thay đổi bước sóng ảnh hưởng trực tiếp đến kết quả giao thoa, đặc biệt là số lượng và vị trí của các vân sáng, vân tối trên màn.
Bài Tập 10: Các Dạng Bài Tập Kết Hợp Khác
Trong phần này, chúng ta sẽ tập trung vào các dạng bài tập kết hợp khác nhau liên quan đến giao thoa ánh sáng, đặc biệt là các bài tập yêu cầu kết hợp nhiều khái niệm vật lý để giải quyết các vấn đề phức tạp. Các bài tập này không chỉ củng cố kiến thức lý thuyết mà còn phát triển khả năng phân tích và giải quyết vấn đề của học sinh.
- Bài Tập Kết Hợp Về Tính Toán Bước Sóng:
Trong các bài tập dạng này, học sinh cần sử dụng các công thức liên quan đến giao thoa ánh sáng để tính toán bước sóng của ánh sáng khi biết các yếu tố như khoảng cách giữa các khe, khoảng cách từ các khe đến màn quan sát và khoảng vân.
- Giả sử trong một thí nghiệm giao thoa ánh sáng với khoảng cách giữa hai khe \(a = 2 \, mm\), khoảng cách từ khe đến màn \(D = 1,2 \, m\), và khoảng vân \(i = 0,36 \, mm\). Hãy tính bước sóng \(\lambda\) của ánh sáng.
- Bài Tập Kết Hợp Về Tính Toán Tần Số:
Trong các bài tập này, học sinh phải kết hợp các công thức của bước sóng và tốc độ ánh sáng để tính tần số của ánh sáng sử dụng trong thí nghiệm.
- Với bước sóng \(\lambda = 600 \, nm\), hãy tính tần số \(f\) của ánh sáng trong thí nghiệm.
- Bài Tập Kết Hợp Về Xác Định Vị Trí Vân Sáng:
Học sinh cần vận dụng công thức xác định vị trí các vân sáng trên màn để tìm ra khoảng cách từ vân sáng chính giữa đến một vân sáng bậc cao hơn.
- Trong thí nghiệm Y-âng, hãy xác định khoảng cách từ vân sáng chính giữa đến vân sáng bậc 4, biết rằng khoảng cách giữa hai khe là \(a = 1,2 \, mm\) và khoảng cách từ khe đến màn là \(D = 0,5 \, m\).
- Bài Tập Kết Hợp Với Ánh Sáng Đơn Sắc:
Các bài tập yêu cầu tính toán và nhận diện các đặc điểm của ánh sáng đơn sắc trong các thí nghiệm giao thoa.
- Ánh sáng đơn sắc có bước sóng từ \(380 \, nm\) đến \(760 \, nm\). Hãy giải thích tại sao ta có thể nhận biết vân chính giữa khi sử dụng ánh sáng trắng trong thí nghiệm Y-âng.
Những bài tập kết hợp này giúp học sinh không chỉ nắm vững lý thuyết mà còn áp dụng hiệu quả trong các tình huống thực tế. Bằng cách luyện tập thường xuyên, học sinh sẽ nâng cao kỹ năng giải quyết các bài toán giao thoa ánh sáng một cách toàn diện và chính xác.