Chủ đề bài 8 giao thoa sóng: Bài viết này sẽ giúp bạn khám phá toàn diện về bài 8 giao thoa sóng, một hiện tượng vật lý thú vị và quan trọng trong chương trình học. Tìm hiểu cách sóng tương tác để tạo ra các hiện tượng giao thoa, ứng dụng trong cuộc sống và các bài tập liên quan để củng cố kiến thức.
Mục lục
- Bài 8: Giao Thoa Sóng - Vật Lý 12
- Mục lục tổng hợp
- Dạng bài tập 1: Tính biên độ dao động tại điểm giao thoa
- Dạng bài tập 2: Xác định vị trí các cực đại giao thoa
- Dạng bài tập 3: Xác định vị trí các cực tiểu giao thoa
- Dạng bài tập 4: Tính bước sóng dựa trên kết quả giao thoa
- Dạng bài tập 5: Tính khoảng cách giữa các vân giao thoa
- Dạng bài tập 6: Tính tần số sóng dựa trên hiện tượng giao thoa
- Dạng bài tập 7: Xác định số vân cực đại trong một khoảng
- Dạng bài tập 8: Tính thời gian để hình thành vân giao thoa
- Dạng bài tập 9: Giải bài toán liên quan đến hai nguồn sóng kết hợp
- Dạng bài tập 10: Bài tập tổng hợp về giao thoa sóng với nhiều nguồn
Bài 8: Giao Thoa Sóng - Vật Lý 12
Bài 8 "Giao thoa sóng" là một nội dung quan trọng trong chương trình Vật Lý lớp 12, nằm trong chủ đề sóng cơ và sóng âm. Bài học này giới thiệu và giải thích hiện tượng giao thoa sóng, một hiện tượng phổ biến trong tự nhiên, cũng như cách tính toán các đại lượng liên quan đến hiện tượng này.
Nội dung chính của bài học
- Khái niệm về hiện tượng giao thoa sóng.
- Điều kiện để có hiện tượng giao thoa.
- Vị trí các cực đại và cực tiểu trong giao thoa sóng.
- Các bài tập vận dụng liên quan đến giao thoa sóng.
Khái niệm về giao thoa sóng
Hiện tượng giao thoa sóng xảy ra khi hai hoặc nhiều sóng kết hợp gặp nhau, tạo ra các vùng có biên độ dao động cực đại và cực tiểu do sự tăng cường hoặc triệt tiêu lẫn nhau của các sóng này. Điều kiện để có hiện tượng giao thoa là các sóng phải có cùng tần số, cùng phương dao động và có hiệu số pha không đổi theo thời gian.
Công thức tính toán
Giả sử có hai nguồn sóng kết hợp \( S_1 \) và \( S_2 \), phương trình sóng tại điểm \( M \) cách hai nguồn lần lượt các khoảng \( d_1 \) và \( d_2 \) được cho bởi:
Trong đó:
- \( A \) là biên độ của sóng tại các nguồn.
- \( \lambda \) là bước sóng.
- \( \omega \) là tần số góc của sóng.
Vị trí cực đại và cực tiểu giao thoa
- Vị trí các cực đại: \( d_2 - d_1 = k\lambda \), với \( k \) là số nguyên.
- Vị trí các cực tiểu: \( d_2 - d_1 = (k + 0.5)\lambda \).
Ví dụ minh họa
Giả sử trên mặt nước có hai nguồn sóng đồng bộ \( S_1 \) và \( S_2 \), cách nhau một khoảng \( d \). Phương trình sóng do hai nguồn này tạo ra tại một điểm \( M \) sẽ có dạng:
Điểm \( M \) sẽ có biên độ dao động cực đại khi \( d_2 - d_1 = k\lambda \), và có biên độ dao động cực tiểu khi \( d_2 - d_1 = (k + 0.5)\lambda \).
Bài tập vận dụng
Bài học cũng cung cấp nhiều bài tập để học sinh có thể thực hành, nhằm củng cố kiến thức về giao thoa sóng, từ việc xác định vị trí cực đại, cực tiểu đến việc tính toán các đại lượng liên quan.
Ví dụ, một bài tập yêu cầu tính vị trí cực đại giao thoa trên mặt nước khi hai nguồn sóng cách nhau 1m, với bước sóng là 0.5m, yêu cầu học sinh tính toán vị trí các cực đại, cực tiểu dựa trên các công thức đã học.
Kết luận
Bài học về giao thoa sóng không chỉ giúp học sinh nắm vững các hiện tượng sóng cơ bản mà còn giúp họ áp dụng các kiến thức này vào việc giải quyết các bài toán thực tế liên quan đến sóng âm, sóng nước và các loại sóng khác trong đời sống hàng ngày.

.png)
Mục lục tổng hợp
Dưới đây là mục lục chi tiết và toàn diện cho bài viết về "Bài 8: Giao Thoa Sóng". Bài viết này giúp bạn hiểu rõ về hiện tượng giao thoa sóng từ cơ bản đến nâng cao, bao gồm các lý thuyết, công thức, và bài tập vận dụng cụ thể.
- Giới thiệu về Giao Thoa Sóng
- Định nghĩa và khái niệm cơ bản
- Ví dụ về giao thoa sóng trong đời sống
- Điều kiện xảy ra Giao Thoa Sóng
- Sóng kết hợp và điều kiện sóng kết hợp
- Các yếu tố ảnh hưởng đến hiện tượng giao thoa
- Phương trình sóng tại các điểm giao thoa
- Phương trình sóng tổng hợp
- Biên độ và pha của sóng giao thoa
- Công thức tính biên độ tại một điểm
- Công thức tính hiệu pha
- Vị trí cực đại và cực tiểu của giao thoa sóng
- Vị trí cực đại
- Vị trí cực tiểu
- Quy tắc xác định vị trí các vân giao thoa
- Bài tập ứng dụng về Giao Thoa Sóng
- Bài tập tính biên độ tại điểm giao thoa
- Bài tập xác định vị trí cực đại và cực tiểu
- Bài tập về sóng trên mặt nước
- Ứng dụng thực tiễn của Giao Thoa Sóng
- Ứng dụng trong công nghệ âm thanh
- Ứng dụng trong đo lường và kiểm tra
- Ứng dụng trong khoa học và kỹ thuật
- Kết luận
- Tổng kết về hiện tượng giao thoa sóng
- Lưu ý khi học về giao thoa sóng
- Hướng dẫn tự học và ôn tập
Dạng bài tập 1: Tính biên độ dao động tại điểm giao thoa
Dạng bài tập này yêu cầu học sinh tính toán biên độ dao động tại một điểm \(M\) trong trường hợp có hai nguồn sóng kết hợp \(S_1\) và \(S_2\). Để giải quyết bài tập này, học sinh cần nắm vững công thức và các bước thực hiện dưới đây.
- Xác định vị trí của điểm M:
Giả sử \(M\) nằm tại vị trí có khoảng cách \(d_1\) từ \(S_1\) và \(d_2\) từ \(S_2\). Các khoảng cách này có thể được xác định dựa trên đề bài hoặc được tính toán từ các thông tin đã cho.
- Tính hiệu đường đi của sóng:
Hiệu đường đi \(\Delta d = d_2 - d_1\) là yếu tố quan trọng ảnh hưởng đến biên độ dao động tại điểm \(M\). Hiệu đường đi này quyết định sự giao thoa tăng cường hay triệt tiêu của sóng tại điểm \(M\).
- Áp dụng công thức biên độ:
Biên độ dao động tại điểm \(M\) được tính bằng công thức:
\[ u_M = 2A \cos\left(\frac{\pi \Delta d}{\lambda}\right) \]- Trong đó \(A\) là biên độ của sóng từ các nguồn \(S_1\) và \(S_2\).
- \(\lambda\) là bước sóng của sóng kết hợp.
- Xác định giá trị biên độ dao động:
Sau khi áp dụng công thức, học sinh sẽ tính toán giá trị của \(u_M\) để xác định biên độ dao động tại điểm \(M\).
- Ví dụ minh họa:
Giả sử hai nguồn sóng kết hợp \(S_1\) và \(S_2\) cách nhau 3 cm, bước sóng \(\lambda = 2 \,cm\), biên độ sóng \(A = 2 \,cm\). Điểm \(M\) nằm trên đường thẳng nối \(S_1\) và \(S_2\) có khoảng cách \(d_1 = 4 \,cm\) từ \(S_1\) và \(d_2 = 6 \,cm\) từ \(S_2\). Ta tính được hiệu đường đi \(\Delta d = 2 \,cm\), biên độ dao động tại \(M\) sẽ là:
\[ u_M = 2 \times 2 \times \cos\left(\frac{\pi \times 2}{2}\right) = 0 \,cm \]Do giá trị cos bằng 0, biên độ dao động tại điểm \(M\) bằng 0, chứng tỏ tại \(M\) có hiện tượng triệt tiêu giao thoa.

Dạng bài tập 2: Xác định vị trí các cực đại giao thoa
Trong dạng bài tập này, học sinh sẽ học cách xác định vị trí các cực đại giao thoa, là những điểm trên mặt phẳng mà tại đó biên độ dao động của sóng đạt giá trị lớn nhất. Để làm được điều này, cần phải sử dụng các công thức và bước thực hiện chi tiết như sau:
- Xác định điều kiện để có cực đại giao thoa:
Cực đại giao thoa xảy ra tại các điểm mà hiệu đường đi của hai sóng đến từ hai nguồn \(S_1\) và \(S_2\) thỏa mãn điều kiện:
\[ \Delta d = d_2 - d_1 = k\lambda \quad \text{với} \quad k \in \mathbb{Z} \]- \(\Delta d\) là hiệu đường đi.
- \(\lambda\) là bước sóng.
- \(k\) là số nguyên (còn gọi là bậc của cực đại).
- Xác định vị trí các cực đại:
Từ điều kiện \(\Delta d = k\lambda\), ta tính được khoảng cách từ các nguồn \(S_1\) và \(S_2\) đến điểm \(M\) (nơi xảy ra cực đại). Các bước xác định vị trí như sau:
- Xác định vị trí tương đối của \(S_1\), \(S_2\) và \(M\) dựa trên đề bài.
- Tính toán khoảng cách \(d_1\) và \(d_2\) từ \(S_1\) và \(S_2\) đến \(M\) sao cho \(\Delta d = k\lambda\).
- Xác định tọa độ hoặc vị trí hình học của điểm \(M\) trên mặt phẳng.
- Ví dụ minh họa:
Giả sử hai nguồn sóng \(S_1\) và \(S_2\) cách nhau 10 cm, với bước sóng \(\lambda = 2 \,cm\). Hãy xác định vị trí các điểm cực đại giao thoa trên đường thẳng nối \(S_1\) và \(S_2\).
- Điều kiện cực đại: \(\Delta d = k\lambda = k \times 2 \,cm\) với \(k\) là số nguyên.
- Xác định các giá trị \(k\) sao cho \(0 \leq k \leq \frac{S_2 - S_1}{\lambda}\).
- Với \(k = 0\): \(\Delta d = 0\), vị trí \(M\) nằm giữa \(S_1\) và \(S_2\).
- Với \(k = 1\): \(\Delta d = 2 \,cm\), xác định vị trí mới của \(M\).
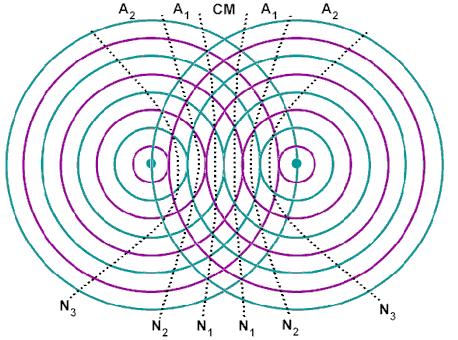
Dạng bài tập 3: Xác định vị trí các cực tiểu giao thoa
Trong dạng bài tập này, học sinh sẽ học cách xác định vị trí các cực tiểu giao thoa, là những điểm trên mặt phẳng mà tại đó biên độ dao động của sóng đạt giá trị nhỏ nhất hoặc bằng 0. Để làm được điều này, cần phải sử dụng các công thức và bước thực hiện chi tiết như sau:
- Xác định điều kiện để có cực tiểu giao thoa:
Cực tiểu giao thoa xảy ra tại các điểm mà hiệu đường đi của hai sóng đến từ hai nguồn \(S_1\) và \(S_2\) thỏa mãn điều kiện:
\[ \Delta d = d_2 - d_1 = \left(k + \frac{1}{2}\right)\lambda \quad \text{với} \quad k \in \mathbb{Z} \]- \(\Delta d\) là hiệu đường đi.
- \(\lambda\) là bước sóng.
- \(k\) là số nguyên (còn gọi là bậc của cực tiểu).
- Xác định vị trí các cực tiểu:
Từ điều kiện \(\Delta d = \left(k + \frac{1}{2}\right)\lambda\), ta tính được khoảng cách từ các nguồn \(S_1\) và \(S_2\) đến điểm \(M\) (nơi xảy ra cực tiểu). Các bước xác định vị trí như sau:
- Xác định vị trí tương đối của \(S_1\), \(S_2\) và \(M\) dựa trên đề bài.
- Tính toán khoảng cách \(d_1\) và \(d_2\) từ \(S_1\) và \(S_2\) đến \(M\) sao cho \(\Delta d = \left(k + \frac{1}{2}\right)\lambda\).
- Xác định tọa độ hoặc vị trí hình học của điểm \(M\) trên mặt phẳng.
- Ví dụ minh họa:
Giả sử hai nguồn sóng \(S_1\) và \(S_2\) cách nhau 10 cm, với bước sóng \(\lambda = 2 \,cm\). Hãy xác định vị trí các điểm cực tiểu giao thoa trên đường thẳng nối \(S_1\) và \(S_2\).
- Điều kiện cực tiểu: \(\Delta d = \left(k + \frac{1}{2}\right)\lambda = \left(k + \frac{1}{2}\right) \times 2 \,cm\) với \(k\) là số nguyên.
- Xác định các giá trị \(k\) sao cho \(0 \leq k \leq \frac{S_2 - S_1}{\lambda}\).
- Với \(k = 0\): \(\Delta d = 1 \,cm\), xác định vị trí của \(M\).
- Với \(k = 1\): \(\Delta d = 3 \,cm\), tiếp tục xác định vị trí mới của \(M\).

Dạng bài tập 4: Tính bước sóng dựa trên kết quả giao thoa
Trong dạng bài tập này, học sinh sẽ học cách tính bước sóng dựa trên các kết quả quan sát được từ hiện tượng giao thoa sóng. Các bước thực hiện chi tiết được trình bày dưới đây nhằm giúp học sinh nắm vững phương pháp và áp dụng hiệu quả trong các bài toán tương tự.
- Xác định khoảng cách giữa các cực đại hoặc cực tiểu:
Đầu tiên, cần xác định khoảng cách giữa các cực đại hoặc cực tiểu liền kề. Khoảng cách này là cơ sở để tính toán bước sóng.
- Khoảng cách giữa hai cực đại hoặc hai cực tiểu liền kề là \(\Delta x = \frac{\lambda}{2}\).
- Đo đạc giá trị thực tế của \(\Delta x\) từ kết quả giao thoa.
- Sử dụng công thức để tính bước sóng:
Với giá trị \(\Delta x\) đã biết, bước sóng được tính theo công thức:
\[ \lambda = 2\Delta x \]- Thay giá trị \(\Delta x\) đã đo đạc vào công thức để tính \(\lambda\).
- Đảm bảo đơn vị đo lường của \(\Delta x\) và \(\lambda\) phải đồng nhất.
- Ví dụ minh họa:
Giả sử khoảng cách giữa hai cực đại giao thoa liền kề là 4 cm. Bước sóng của sóng là bao nhiêu?
- Áp dụng công thức: \(\lambda = 2 \times 4 \,cm = 8 \,cm\).
- Như vậy, bước sóng \(\lambda\) trong trường hợp này là 8 cm.
XEM THÊM:
Dạng bài tập 5: Tính khoảng cách giữa các vân giao thoa
Trong dạng bài tập này, học sinh sẽ học cách tính khoảng cách giữa các vân giao thoa - tức là khoảng cách giữa các cực đại hoặc cực tiểu liên tiếp trong hiện tượng giao thoa sóng. Quá trình tính toán bao gồm các bước sau:
- Xác định công thức khoảng cách giữa các vân giao thoa:
Khoảng cách giữa hai vân giao thoa liên tiếp được xác định bởi công thức:
\[ i = \frac{\lambda D}{a} \]- \(i\) là khoảng cách giữa hai vân sáng (hoặc tối) liên tiếp.
- \(\lambda\) là bước sóng của sóng giao thoa.
- \(D\) là khoảng cách từ các nguồn sóng đến màn quan sát.
- \(a\) là khoảng cách giữa hai nguồn sóng.
- Sử dụng công thức để tính khoảng cách giữa các vân:
Với giá trị \(\lambda\), \(D\), và \(a\) đã biết, ta có thể dễ dàng tính toán được khoảng cách \(i\) giữa các vân giao thoa.
- Thay giá trị \(\lambda\), \(D\), và \(a\) vào công thức.
- Đảm bảo đơn vị của các đại lượng phải đồng nhất trước khi thực hiện tính toán.
- Ví dụ minh họa:
Giả sử bước sóng \(\lambda = 2 \,cm\), khoảng cách giữa hai nguồn sóng \(a = 10 \,cm\), và khoảng cách từ nguồn đến màn \(D = 1 \,m\). Hãy tính khoảng cách giữa hai vân sáng liên tiếp.
- Áp dụng công thức: \(i = \frac{2 \times 100}{10} \,cm = 20 \,cm\).
- Như vậy, khoảng cách giữa hai vân sáng liên tiếp là 20 cm.

Dạng bài tập 6: Tính tần số sóng dựa trên hiện tượng giao thoa
Trong hiện tượng giao thoa sóng, tần số của sóng là một trong những yếu tố quan trọng có thể tính toán dựa trên các thông số khác nhau như bước sóng, khoảng cách giữa các vân giao thoa, hoặc thời gian để một số vân giao thoa nhất định xuất hiện. Để hiểu rõ hơn, chúng ta hãy cùng xem qua các bước tính tần số sóng.
1. Phân tích hiện tượng giao thoa
Khi hai nguồn sóng \(S_1\) và \(S_2\) dao động cùng pha hoặc ngược pha, chúng tạo ra hiện tượng giao thoa. Các điểm trên mặt nước có thể dao động với biên độ cực đại (cực đại giao thoa) hoặc dao động với biên độ bằng không (cực tiểu giao thoa).
2. Công thức cơ bản
Để tính tần số sóng \(f\), ta có thể sử dụng các công thức liên quan đến khoảng cách giữa các vân giao thoa:
- Khoảng cách giữa hai vân cực đại (hoặc cực tiểu) liên tiếp \(i\) được tính theo công thức: \[ i = \frac{\lambda \cdot D}{d} \] với \( \lambda \) là bước sóng, \( D \) là khoảng cách từ hai nguồn sóng đến màn, và \( d \) là khoảng cách giữa hai nguồn sóng.
- Từ bước sóng \( \lambda \), ta có thể tính tần số sóng \( f \) dựa trên tốc độ truyền sóng \( v \): \[ f = \frac{v}{\lambda} \] với \( v \) là tốc độ truyền sóng trong môi trường.
3. Ví dụ minh họa
Giả sử ta có khoảng cách giữa hai nguồn sóng \( S_1S_2 = 10 \, cm \) và khoảng cách từ nguồn đến màn \( D = 1 \, m \). Tốc độ truyền sóng trong môi trường là \( v = 340 \, m/s \). Nếu khoảng cách giữa hai vân cực đại liên tiếp đo được là \( i = 2 \, cm \), ta có thể tính tần số sóng như sau:
- Tính bước sóng \( \lambda \): \[ \lambda = \frac{i \cdot d}{D} = \frac{2 \times 10^{-2} \cdot 10^{-1}}{1} = 2 \times 10^{-3} \, m = 2 \, mm \]
- Tính tần số \( f \): \[ f = \frac{v}{\lambda} = \frac{340}{2 \times 10^{-3}} = 170 \times 10^3 \, Hz = 170 \, kHz \]
Vậy, tần số sóng trong trường hợp này là \( 170 \, kHz \).
4. Lưu ý
- Để có hiện tượng giao thoa ổn định, hai nguồn sóng phải có cùng tần số và biên độ.
- Công thức tính tần số dựa trên bước sóng chỉ áp dụng khi biết trước tốc độ truyền sóng.

Dạng bài tập 7: Xác định số vân cực đại trong một khoảng
Để xác định số vân cực đại trong một khoảng giữa hai nguồn sóng \( S_1 \) và \( S_2 \), ta sử dụng các bước sau:
- Xác định bước sóng \(\lambda\): Trước tiên, ta cần biết bước sóng \(\lambda\) của sóng. Bước sóng được tính bằng công thức: \[ \lambda = \frac{v}{f} \] trong đó \( v \) là vận tốc sóng và \( f \) là tần số sóng.
- Tính số vân cực đại: Số vân cực đại trong khoảng giữa hai nguồn sóng được xác định bằng công thức: \[ N = \frac{2D}{\lambda} \] trong đó \( D \) là khoảng cách giữa hai nguồn \( S_1 \) và \( S_2 \). Số lượng vân cực đại \( N \) được tính bằng cách đếm số nguyên \( k \) thỏa mãn điều kiện: \[ -\frac{D}{\lambda} \leq k \leq \frac{D}{\lambda} \] với \( k \) là bậc của vân cực đại.
- Xác định vị trí các vân cực đại: Vị trí các vân cực đại trên đoạn thẳng nối \( S_1 \) và \( S_2 \) được xác định bằng cách tính các giá trị \( d_1 \) và \( d_2 \) sao cho hiệu đường đi của hai sóng từ \( S_1 \) và \( S_2 \) đến điểm trên đoạn đó thỏa mãn: \[ d_2 - d_1 = k\lambda \] Các điểm này chính là các vị trí của vân cực đại.
Bằng cách áp dụng các công thức trên, bạn có thể xác định chính xác số lượng và vị trí của các vân cực đại trong khoảng giữa hai nguồn sóng. Đây là một kỹ năng quan trọng trong việc giải các bài toán về giao thoa sóng trong vật lý.
Dạng bài tập 8: Tính thời gian để hình thành vân giao thoa
Để tính thời gian cần thiết để hình thành một vân giao thoa, ta cần xem xét các yếu tố liên quan đến sự giao thoa của sóng, bao gồm tần số sóng, bước sóng và khoảng cách giữa hai nguồn phát sóng. Phương pháp giải quyết dạng bài tập này như sau:
- Xác định tần số \(f\) và bước sóng \(\lambda\) của sóng dựa trên dữ liệu bài toán.
- Tìm khoảng cách giữa hai nguồn sóng \(S_1\) và \(S_2\) trên mặt phẳng.
- Xác định khoảng cách giữa hai vân cực đại hoặc cực tiểu liên tiếp \(\Delta x\), được tính bằng công thức: \[ \Delta x = \frac{\lambda \times D}{d} \] trong đó \(D\) là khoảng cách từ hai nguồn sóng đến màn hình quan sát, và \(d\) là khoảng cách giữa hai nguồn sóng.
- Xác định thời gian \(t\) để hình thành một vân giao thoa tại một vị trí nhất định, thường được tính bằng công thức: \[ t = \frac{1}{f} \] hoặc thời gian cần để sóng di chuyển khoảng cách bằng bước sóng.
- Áp dụng các giá trị vào công thức để tính ra thời gian \(t\).
Ví dụ:
Hai nguồn sóng \(S_1\) và \(S_2\) dao động đồng bộ với tần số \(f = 25\) Hz, khoảng cách giữa hai nguồn là \(d = 1\) m, khoảng cách từ hai nguồn đến màn hình là \(D = 2\) m. Bước sóng của sóng là \(\lambda = 0.1\) m. Tính thời gian để một vân giao thoa hình thành tại điểm M trên màn hình.
- Bước 1: Tính khoảng cách giữa hai vân cực đại liên tiếp: \[ \Delta x = \frac{\lambda \times D}{d} = \frac{0.1 \times 2}{1} = 0.2 \text{ m} \]
- Bước 2: Tính thời gian để hình thành một vân giao thoa: \[ t = \frac{1}{f} = \frac{1}{25} = 0.04 \text{ giây} \]
Vậy, thời gian cần thiết để hình thành một vân giao thoa tại điểm M là 0.04 giây.

Dạng bài tập 9: Giải bài toán liên quan đến hai nguồn sóng kết hợp
Trong bài toán giao thoa sóng, hai nguồn sóng kết hợp là hai nguồn phát ra sóng có cùng tần số, cùng pha hoặc độ lệch pha không đổi theo thời gian. Để giải quyết các bài toán liên quan đến hai nguồn sóng kết hợp, chúng ta thường phải xác định vị trí các cực đại và cực tiểu giao thoa, tính khoảng cách giữa các vân, và tính toán các đại lượng khác liên quan.
Ví dụ:
Cho hai nguồn sóng kết hợp \( S_1 \) và \( S_2 \) phát ra hai sóng có cùng biên độ và cùng pha với phương trình sóng:
- Sóng từ \( S_1 \): \( u_1 = A \cos(\omega t - k d_1) \)
- Sóng từ \( S_2 \): \( u_2 = A \cos(\omega t - k d_2) \)
Tại điểm \( M \) trên mặt phẳng chứa hai nguồn, dao động tổng hợp là:
\[ u_M = u_1 + u_2 = 2A \cos \left(\frac{k (d_1 - d_2)}{2}\right) \cos \left(\omega t - \frac{k (d_1 + d_2)}{2}\right) \]
Trong đó:
- \( A \) là biên độ của sóng
- \( \omega \) là tần số góc
- \( k = \frac{2\pi}{\lambda} \) là số sóng, với \( \lambda \) là bước sóng
- \( d_1 \) và \( d_2 \) lần lượt là khoảng cách từ \( M \) đến \( S_1 \) và \( S_2 \)
Để tìm các điểm có dao động cực đại, ta sử dụng điều kiện:
\[ \Delta d = d_1 - d_2 = k \lambda \quad \text{với } k \in \mathbb{Z} \]
Để tìm các điểm có dao động cực tiểu, ta sử dụng điều kiện:
\[ \Delta d = d_1 - d_2 = \left(k + \frac{1}{2}\right) \lambda \quad \text{với } k \in \mathbb{Z} \]
Ví dụ cụ thể: Giả sử \( S_1 \) và \( S_2 \) cách nhau một khoảng \( d \), bước sóng là \( \lambda = 0.5 \, \text{m} \). Hãy xác định vị trí của các vân cực đại và cực tiểu trên đường nối hai nguồn.
- Tính khoảng cách giữa hai vân cực đại liên tiếp:
\[ i = \frac{\lambda}{2} = \frac{0.5}{2} = 0.25 \, \text{m} \]
- Tìm vị trí các vân cực đại:
\[ x_k = k \cdot 0.25 \, \text{m} \quad \text{với } k \in \mathbb{Z} \]
- Tìm vị trí các vân cực tiểu:
\[ x_k = \left(k + \frac{1}{2}\right) \cdot 0.25 \, \text{m} \quad \text{với } k \in \mathbb{Z} \]
Qua bài toán này, chúng ta thấy rằng việc hiểu rõ điều kiện giao thoa và công thức tính toán liên quan là rất quan trọng để giải quyết các bài tập về giao thoa sóng.
Dạng bài tập 10: Bài tập tổng hợp về giao thoa sóng với nhiều nguồn
Trong các bài toán về giao thoa sóng với nhiều nguồn, chúng ta thường phải xử lý các tình huống mà số lượng nguồn sóng dao động cùng pha hoặc ngược pha không chỉ là hai, mà có thể là ba hoặc nhiều hơn. Dạng bài này đòi hỏi học sinh phải hiểu rõ nguyên lý cơ bản của hiện tượng giao thoa sóng và áp dụng linh hoạt các công thức toán học để giải quyết.
Để giải các bài toán tổng hợp về giao thoa sóng với nhiều nguồn, bạn có thể làm theo các bước sau:
- Phân tích đề bài: Xác định số lượng nguồn sóng, khoảng cách giữa các nguồn và tần số hoặc bước sóng của các sóng. Từ đó, suy ra các đại lượng liên quan như độ lệch pha giữa các nguồn.
- Xác định các điểm có biên độ cực đại và cực tiểu: Đối với mỗi điểm trong không gian, tính tổng biên độ sóng từ tất cả các nguồn. Biên độ tổng hợp tại một điểm sẽ phụ thuộc vào sự giao thoa của sóng từ các nguồn. Điểm có biên độ cực đại khi tổng hợp biên độ từ các sóng là lớn nhất, và có biên độ cực tiểu khi tổng hợp biên độ từ các sóng là nhỏ nhất hoặc bằng 0.
- Sử dụng các công thức toán học: Để tính biên độ sóng tổng hợp tại một điểm, bạn có thể sử dụng công thức giao thoa tổng quát: \[ A_M = 2A \left|\cos\left(\pi \frac{d_2 - d_1}{\lambda}\right)\right| \] Trong đó, \( d_1 \) và \( d_2 \) là khoảng cách từ các nguồn đến điểm M, và \( \lambda \) là bước sóng. Nếu có nhiều hơn hai nguồn, công thức cần được điều chỉnh tương ứng.
- Xác định các khoảng cách và số vân giao thoa: Dựa trên các điểm có biên độ cực đại và cực tiểu, tính toán khoảng cách giữa các vân giao thoa và xác định số vân trong khoảng đã cho.
- Giải bài toán thực tế: Áp dụng các bước trên vào các bài toán cụ thể để tìm ra đáp án chính xác. Ví dụ, tìm số vân cực đại trong một khoảng xác định hoặc tính khoảng cách giữa các vân cực đại và cực tiểu trong trường hợp nhiều nguồn sóng kết hợp.
Ví dụ:
- Cho ba nguồn sóng kết hợp có cùng pha, cùng tần số, và đặt trên một đường thẳng. Xác định số điểm có biên độ cực đại trên đoạn thẳng nối giữa hai nguồn ngoài cùng.
- Bài toán sẽ yêu cầu tính toán biên độ tổng hợp tại các điểm trên đoạn thẳng này và xác định các vị trí có biên độ cực đại bằng cách giải phương trình tổng biên độ.