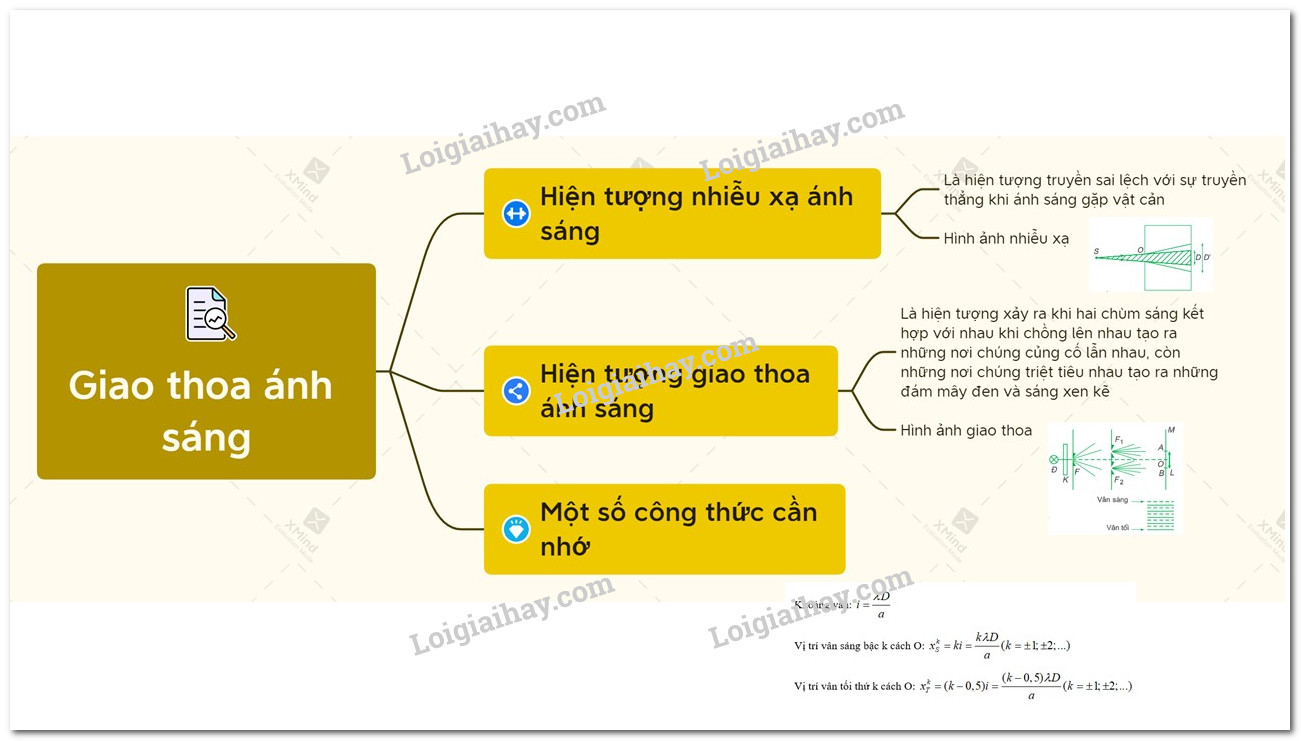
Chủ đề hiện tượng giao thoa ánh sáng chỉ quan sát được: Hiện tượng giao thoa ánh sáng chỉ quan sát được trong những điều kiện đặc biệt, chứng minh tính chất sóng của ánh sáng. Bài viết này sẽ khám phá sâu hơn về hiện tượng này, từ nguyên lý cơ bản đến ứng dụng thực tiễn trong khoa học và công nghệ.
Mục lục
- Hiện Tượng Giao Thoa Ánh Sáng
- Mục Lục
- 1. Bài Tập Ứng Dụng Về Giao Thoa Ánh Sáng
- Bài Tập 1: Tính Khoảng Vân Trong Thí Nghiệm Young
- Bài Tập 2: Xác Định Vị Trí Vân Sáng Thứ n
- Bài Tập 3: Tính Khoảng Cách Giữa Hai Vân Sáng Liên Tiếp
- Bài Tập 4: Xác Định Độ Lệch Pha Giữa Hai Sóng Kết Hợp
- Bài Tập 5: Tính Vị Trí Của Vân Tối Đầu Tiên
- Bài Tập 6: Ứng Dụng Giao Thoa Ánh Sáng Để Đo Chiều Dài Sóng
- Bài Tập 7: Tính Tần Số Của Ánh Sáng Dựa Trên Giao Thoa
- Bài Tập 8: Xác Định Số Vân Sáng Trên Màn Hình
- Bài Tập 9: Tính Toán Liên Quan Đến Hiệu Số Đường Đi Của Sóng
- Bài Tập 10: Bài Tập Tổng Hợp Về Giao Thoa Ánh Sáng
Hiện Tượng Giao Thoa Ánh Sáng
Hiện tượng giao thoa ánh sáng là một trong những hiện tượng tiêu biểu của tính chất sóng của ánh sáng. Hiện tượng này chỉ có thể quan sát được khi hai nguồn sáng kết hợp, thường là từ cùng một nguồn sáng hoặc từ hai nguồn sáng có tần số rất gần nhau.
Điều Kiện Để Quan Sát Hiện Tượng Giao Thoa Ánh Sáng
- Các nguồn sáng phải là nguồn sáng kết hợp, nghĩa là chúng có cùng tần số hoặc tần số rất gần nhau.
- Khoảng cách giữa các nguồn sáng phải đủ nhỏ để các sóng có thể giao thoa.
- Môi trường truyền ánh sáng phải đồng nhất, không có sự nhiễu loạn.
Thí Nghiệm Young và Ứng Dụng
Thí nghiệm nổi tiếng của Thomas Young năm 1803 đã chứng minh sự tồn tại của hiện tượng giao thoa ánh sáng. Trong thí nghiệm này, ánh sáng được chiếu qua hai khe hẹp và sau đó được quan sát trên một màn hình. Kết quả là trên màn hình xuất hiện các vân sáng và tối xen kẽ, biểu thị sự giao thoa giữa hai sóng ánh sáng từ hai khe.
Công thức xác định vị trí các vân sáng tối:
Các Công Thức Liên Quan
- Khoảng vân: \[i = \frac{\lambda D}{a}\]
- Điều kiện để có vân sáng: \(\delta = m\lambda\)
- Điều kiện để có vân tối: \(\delta = (2m+1)\frac{\lambda}{2}\)
Ứng Dụng Thực Tiễn
Hiện tượng giao thoa ánh sáng được ứng dụng trong nhiều lĩnh vực khác nhau như:
- Trong công nghệ quang học, các thiết bị giao thoa kế được sử dụng để đo độ dài, khoảng cách và độ chính xác cao.
- Trong nghiên cứu khoa học, giao thoa ánh sáng giúp nghiên cứu các tính chất của sóng ánh sáng, đồng thời là minh chứng cho tính chất sóng của ánh sáng.
- Trong công nghệ, giao thoa ánh sáng được ứng dụng để kiểm tra độ chính xác của bề mặt và trong việc sản xuất các linh kiện quang học.
.png)
Mục Lục
1. Hiện Tượng Giao Thoa Ánh Sáng Là Gì?
2. Nguyên Lý Hoạt Động Của Giao Thoa Ánh Sáng
3. Các Điều Kiện Cần Thiết Để Quan Sát Giao Thoa Ánh Sáng
4. Thí Nghiệm Young Và Sự Chứng Minh Tính Chất Sóng Của Ánh Sáng
5. Ứng Dụng Của Giao Thoa Ánh Sáng Trong Khoa Học Và Công Nghệ
6. Phân Tích Các Loại Giao Thoa: Giao Thoa Xây Dựng Và Giao Thoa Phá Hủy
7. Công Thức Toán Học Trong Hiện Tượng Giao Thoa Ánh Sáng
8. Giao Thoa Ánh Sáng Trong Đời Sống Hàng Ngày: Thí Dụ Và Ứng Dụng
9. Bài Tập Về Giao Thoa Ánh Sáng Có Lời Giải
10. Câu Hỏi Thường Gặp Về Giao Thoa Ánh Sáng
1. Bài Tập Ứng Dụng Về Giao Thoa Ánh Sáng
Dưới đây là một số bài tập ứng dụng giúp hiểu rõ hơn về hiện tượng giao thoa ánh sáng. Các bài tập này sẽ cung cấp cho bạn cách tính toán và phân tích các hiện tượng giao thoa trong thực tế.
Bài Tập 1: Tính Toán Vị Trí Cực Đại Và Cực Tiểu
Cho hai khe sáng \(S_1\) và \(S_2\) cách nhau một khoảng \(d = 0.1 mm\), chiếu bằng ánh sáng đơn sắc có bước sóng \(\lambda = 600 nm\). Tính khoảng cách giữa các vân sáng liên tiếp trên màn cách hai khe \(D = 1 m\).
Lời Giải: Ta sử dụng công thức:
\[
\Delta x = \frac{\lambda \cdot D}{d}
\]Thay các giá trị vào, ta có:
\[
\Delta x = \frac{600 \times 10^{-9} \cdot 1}{0.1 \times 10^{-3}} = 6 \times 10^{-3} m = 6 mm
\]Vậy khoảng cách giữa các vân sáng liên tiếp là \(6 mm\).
Bài Tập 2: Xác Định Bước Sóng Ánh Sáng
Một thí nghiệm giao thoa được thực hiện với khoảng cách giữa hai khe là \(0.2 mm\) và khoảng cách từ khe đến màn là \(2 m\). Nếu khoảng cách giữa hai vân sáng liên tiếp đo được là \(4 mm\), hãy xác định bước sóng của ánh sáng được sử dụng.
Lời Giải: Sử dụng công thức:
\[
\lambda = \frac{\Delta x \cdot d}{D}
\]Thay các giá trị vào, ta có:
\[
\lambda = \frac{4 \times 10^{-3} \cdot 0.2 \times 10^{-3}}{2} = 4 \times 10^{-7} m = 400 nm
\]Vậy bước sóng của ánh sáng là \(400 nm\).
Bài Tập 3: Tính Số Vân Sáng Quan Sát Được
Một thí nghiệm giao thoa thực hiện với ánh sáng có bước sóng \(600 nm\), hai khe cách nhau \(0.1 mm\), màn quan sát cách hai khe \(2 m\). Tính số vân sáng quan sát được trên màn trong phạm vi \(10 mm\) tính từ vân sáng trung tâm.
Lời Giải: Sử dụng công thức:
\[
n = \frac{L}{\Delta x}
\]Với \(L\) là khoảng cách từ vân trung tâm đến vị trí cần tính:
\[
\Delta x = \frac{\lambda \cdot D}{d} = \frac{600 \times 10^{-9} \cdot 2}{0.1 \times 10^{-3}} = 12 \times 10^{-3} m = 12 mm
\]Số vân sáng quan sát được là:
\[
n = \frac{10}{12} \approx 0.83 \text{ vân}
\]Vậy trong phạm vi \(10 mm\) tính từ vân sáng trung tâm, có thể quan sát được 1 vân sáng.

Bài Tập 1: Tính Khoảng Vân Trong Thí Nghiệm Young
Thí nghiệm giao thoa ánh sáng của Young là một trong những thí nghiệm kinh điển để chứng minh tính chất sóng của ánh sáng. Dưới đây là bài tập tính khoảng vân trong thí nghiệm Young, với các bước hướng dẫn chi tiết giúp bạn hiểu rõ hơn về hiện tượng này.
Đề Bài:
Trong thí nghiệm Young, hai khe hẹp \( S_1 \) và \( S_2 \) cách nhau một khoảng \( d = 0.5 mm \). Ánh sáng đơn sắc có bước sóng \( \lambda = 600 nm \) chiếu vào hai khe. Màn quan sát cách hai khe một khoảng \( D = 2 m \). Tính khoảng vân giao thoa \( \Delta x \) trên màn.
Lời Giải:
Bước 1: Xác định công thức tính khoảng vân:
\[
\Delta x = \frac{\lambda \cdot D}{d}
\]Bước 2: Thay các giá trị đã cho vào công thức:
\[
\Delta x = \frac{600 \times 10^{-9} \times 2}{0.5 \times 10^{-3}}
\]Bước 3: Thực hiện phép tính:
\[
\Delta x = \frac{1200 \times 10^{-9}}{0.5 \times 10^{-3}} = 2.4 \times 10^{-3} m = 2.4 mm
\]Vậy, khoảng vân \( \Delta x \) trong thí nghiệm này là \( 2.4 mm \).
Nhận Xét:
Kết quả này cho thấy khoảng cách giữa các vân sáng liên tiếp trên màn quan sát trong thí nghiệm Young là \( 2.4 mm \), một khoảng cách đủ lớn để có thể dễ dàng quan sát bằng mắt thường.

Bài Tập 2: Xác Định Vị Trí Vân Sáng Thứ n
Trong thí nghiệm giao thoa ánh sáng, việc xác định vị trí của vân sáng thứ \(n\) giúp hiểu rõ hơn về tính chất sóng của ánh sáng. Bài tập dưới đây hướng dẫn bạn cách tính toán vị trí của các vân sáng này.
Đề Bài:
Trong thí nghiệm Young, hai khe hẹp cách nhau một khoảng \(d = 0.8 mm\). Ánh sáng đơn sắc có bước sóng \(\lambda = 500 nm\) được chiếu vào hai khe, và màn quan sát cách hai khe một khoảng \(D = 1.5 m\). Tính vị trí của vân sáng thứ \(n = 3\) trên màn.
Lời Giải:
Bước 1: Xác định công thức tính vị trí của vân sáng thứ \(n\):
\[
x_n = \frac{n \cdot \lambda \cdot D}{d}
\]Bước 2: Thay các giá trị đã cho vào công thức:
\[
x_3 = \frac{3 \cdot 500 \times 10^{-9} \cdot 1.5}{0.8 \times 10^{-3}}
\]Bước 3: Thực hiện phép tính:
\[
x_3 = \frac{2250 \times 10^{-9}}{0.8 \times 10^{-3}} = 2.8125 \times 10^{-3} m = 2.8125 mm
\]Vậy, vị trí của vân sáng thứ 3 trên màn là \(2.8125 mm\) tính từ vân trung tâm.
Nhận Xét:
Vân sáng thứ 3 nằm khá gần vân trung tâm, giúp chúng ta dễ dàng quan sát và đo đạc trong thí nghiệm.

Bài Tập 3: Tính Khoảng Cách Giữa Hai Vân Sáng Liên Tiếp
Bài tập này giúp bạn hiểu rõ hơn về hiện tượng giao thoa ánh sáng và cách xác định khoảng cách giữa hai vân sáng liên tiếp trong thí nghiệm giao thoa ánh sáng của Young.
Đề Bài:
Trong thí nghiệm Young, hai khe hẹp cách nhau một khoảng \(d = 0.5 mm\). Ánh sáng đơn sắc có bước sóng \(\lambda = 600 nm\) được chiếu vào hai khe, và màn quan sát cách hai khe một khoảng \(D = 2 m\). Hãy tính khoảng cách giữa hai vân sáng liên tiếp trên màn quan sát.
Lời Giải:
Bước 1: Xác định công thức tính khoảng cách giữa hai vân sáng liên tiếp (khoảng vân):
\[
i = \frac{\lambda \cdot D}{d}
\]Bước 2: Thay các giá trị đã cho vào công thức:
\[
i = \frac{600 \times 10^{-9} \cdot 2}{0.5 \times 10^{-3}}
\]Bước 3: Thực hiện phép tính:
\[
i = \frac{1200 \times 10^{-9}}{0.5 \times 10^{-3}} = 2.4 \times 10^{-3} m = 2.4 mm
\]Vậy, khoảng cách giữa hai vân sáng liên tiếp trên màn là \(2.4 mm\).
Nhận Xét:
Khoảng cách giữa hai vân sáng liên tiếp càng nhỏ thì hiện tượng giao thoa càng rõ nét, giúp dễ dàng quan sát và phân tích trong thí nghiệm.
XEM THÊM:
Bài Tập 4: Xác Định Độ Lệch Pha Giữa Hai Sóng Kết Hợp
Trong bài tập này, chúng ta sẽ tính toán độ lệch pha giữa hai sóng kết hợp trong hiện tượng giao thoa ánh sáng, dựa trên các thông số đã cho.
Đề Bài:
Hai nguồn sáng kết hợp A và B phát ra ánh sáng có cùng bước sóng \(\lambda = 500 nm\) và có độ lệch pha ban đầu là \(\phi_0 = 0\). Hai sóng đến điểm M trên màn giao thoa có hiệu đường đi là \(\Delta l = 1.25 \mu m\). Tính độ lệch pha giữa hai sóng tại điểm M.
Lời Giải:
Bước 1: Xác định công thức tính độ lệch pha giữa hai sóng kết hợp:
\[
\Delta \phi = \frac{2\pi \Delta l}{\lambda}
\]Bước 2: Thay các giá trị đã cho vào công thức:
\[
\Delta \phi = \frac{2\pi \times 1.25 \times 10^{-6}}{500 \times 10^{-9}}
\]Bước 3: Thực hiện phép tính:
\[
\Delta \phi = \frac{2\pi \times 1.25}{0.5} = 5\pi rad
\]Vậy, độ lệch pha giữa hai sóng tại điểm M là \(5\pi rad\).
Nhận Xét:
Độ lệch pha giữa hai sóng càng lớn thì độ tương phản giữa các vân sáng và vân tối trong giao thoa càng rõ rệt, giúp dễ dàng quan sát và phân tích kết quả thí nghiệm.

Bài Tập 5: Tính Vị Trí Của Vân Tối Đầu Tiên
Để tính vị trí của vân tối đầu tiên trong thí nghiệm giao thoa ánh sáng, chúng ta cần sử dụng công thức sau:
\[ y_k = \left(k + \frac{1}{2}\right)\frac{\lambda D}{a} \]
Trong đó:
- \(\lambda\) là bước sóng của ánh sáng sử dụng (đơn vị: mét).
- D là khoảng cách từ nguồn sáng đến màn quan sát (đơn vị: mét).
- a là khoảng cách giữa hai khe hẹp (đơn vị: mét).
- k là số thứ tự của vân tối (k = 0 cho vân tối đầu tiên).
Ví dụ: Giả sử trong một thí nghiệm, ánh sáng có bước sóng \(\lambda = 600 \, nm\), khoảng cách giữa hai khe là \(a = 0,5 \, mm\) và khoảng cách từ nguồn sáng đến màn quan sát là \(D = 2 \, m\). Tính vị trí của vân tối đầu tiên trên màn.
Thay các giá trị vào công thức:
\[ y_0 = \left(0 + \frac{1}{2}\right)\frac{600 \times 10^{-9} \times 2}{0,5 \times 10^{-3}} \]
Kết quả:
\[ y_0 = \frac{1}{2} \times \frac{1,2 \times 10^{-6}}{0,5 \times 10^{-3}} = 1,2 \, mm \]
Vậy, vị trí của vân tối đầu tiên cách vị trí trung tâm một khoảng là 1,2 mm.

Bài Tập 6: Ứng Dụng Giao Thoa Ánh Sáng Để Đo Chiều Dài Sóng
Trong hiện tượng giao thoa ánh sáng, "khoảng vân" là khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp trên màn quan sát. Khoảng vân được ký hiệu là \(x\) và nó thể hiện sự đều đặn trong việc phân bố các vân sáng và vân tối khi hai sóng ánh sáng giao thoa với nhau.
Công Thức Tính Khoảng Vân
Khoảng vân được xác định theo công thức:
\[ x = \frac{\lambda \cdot L}{d} \]
Trong đó:
- \(x\) là khoảng vân - khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp.
- \(\lambda\) là chiều dài sóng ánh sáng.
- \(L\) là khoảng cách từ hai khe tới màn quan sát.
- \(d\) là khoảng cách giữa hai khe sáng trong thí nghiệm Young.
Ý Nghĩa Của Khoảng Vân
Khoảng vân giúp xác định độ phân bố và sự đều đặn của các vân sáng và vân tối trên màn hình. Khoảng vân càng lớn, các vân sáng và tối sẽ càng cách xa nhau; ngược lại, khoảng vân càng nhỏ, các vân sẽ càng gần nhau.
Ảnh Hưởng Đến Kết Quả Thí Nghiệm
Khoảng vân phụ thuộc vào chiều dài sóng của ánh sáng và các yếu tố thí nghiệm khác như khoảng cách giữa hai khe \(d\) và khoảng cách từ khe đến màn \(L\). Các thay đổi trong các yếu tố này sẽ làm thay đổi giá trị của khoảng vân, từ đó ảnh hưởng đến sự quan sát của hiện tượng giao thoa ánh sáng.
Bài Tập 7: Tính Tần Số Của Ánh Sáng Dựa Trên Giao Thoa
Để tính tần số của ánh sáng dựa trên hiện tượng giao thoa, ta cần sử dụng mối quan hệ giữa tần số, bước sóng và tốc độ truyền của ánh sáng. Công thức cơ bản để xác định tần số của ánh sáng là:
Trong đó:
- f là tần số của ánh sáng (đơn vị Hz).
- v là vận tốc của ánh sáng trong môi trường truyền (đơn vị m/s).
- \lambda là bước sóng của ánh sáng (đơn vị m).
Để giải quyết bài tập này, ta cần thực hiện theo các bước sau:
- Xác định bước sóng \(\lambda\) của ánh sáng sử dụng trong thí nghiệm giao thoa.
- Sử dụng tốc độ ánh sáng trong không khí, giá trị này là \(v = 3 \times 10^8\) m/s.
- Thay các giá trị này vào công thức trên để tính tần số của ánh sáng.
Ví dụ:
Giả sử trong thí nghiệm, bước sóng của ánh sáng đo được là \(\lambda = 600 \, \text{nm}\) (nanomet). Tốc độ của ánh sáng trong không khí là \(v = 3 \times 10^8 \, \text{m/s}\). Áp dụng công thức:
Như vậy, tần số của ánh sáng trong thí nghiệm này là \(5 \times 10^{14}\) Hz.
Các bước này có thể được áp dụng cho các giá trị khác nhau của bước sóng để tính toán tần số ánh sáng trong nhiều trường hợp khác nhau.

Bài Tập 8: Xác Định Số Vân Sáng Trên Màn Hình
Trong bài tập này, chúng ta sẽ xác định số vân sáng trên màn hình quan sát trong thí nghiệm giao thoa ánh sáng. Để làm được điều này, ta cần áp dụng các công thức liên quan đến hiện tượng giao thoa ánh sáng trong thí nghiệm Y-âng.
Bước 1: Xác định khoảng vân \(i\).
Khoảng vân \(i\) là khoảng cách giữa hai vân sáng liên tiếp hoặc hai vân tối liên tiếp. Công thức tính khoảng vân là:
Trong đó:
- \(\lambda\) là bước sóng của ánh sáng đơn sắc.
- \(D\) là khoảng cách từ màn hình chứa hai khe đến màn quan sát.
- \(a\) là khoảng cách giữa hai khe sáng.
Bước 2: Xác định vị trí các vân sáng trên màn hình.
Vị trí các vân sáng trên màn hình được xác định bởi công thức:
Trong đó:
- \(k\) là bậc của vân sáng, với \(k\) là số nguyên (0, ±1, ±2,...).
- \(x_k\) là khoảng cách từ vị trí vân sáng trung tâm đến vân sáng thứ \(k\).
Bước 3: Xác định số vân sáng quan sát được.
Số vân sáng quan sát được trên màn hình sẽ phụ thuộc vào kích thước của màn và các thông số của thí nghiệm. Số vân sáng \(N\) được tính bằng cách xác định số giá trị nguyên của \(k\) mà vẫn nằm trong phạm vi chiều dài của màn hình.
Giả sử màn hình có chiều dài \(L\), thì số vân sáng có thể xác định bằng cách:
Kết luận: Số vân sáng trên màn hình được xác định dựa trên bước sóng ánh sáng sử dụng, khoảng cách giữa hai khe, và khoảng cách từ hai khe đến màn hình. Bằng cách tính toán các giá trị này, ta có thể xác định chính xác số lượng vân sáng xuất hiện trên màn hình trong thí nghiệm giao thoa ánh sáng.
Bài Tập 9: Tính Toán Liên Quan Đến Hiệu Số Đường Đi Của Sóng
Trong bài tập này, chúng ta sẽ thực hiện các phép tính liên quan đến hiệu số đường đi của sóng trong hiện tượng giao thoa ánh sáng. Đây là một phần quan trọng để xác định vị trí các vân sáng và vân tối trong các thí nghiệm liên quan đến giao thoa.
Đề bài: Xét hai nguồn sáng kết hợp \( S_1 \) và \( S_2 \) phát ra sóng có cùng bước sóng \(\lambda = 600\;nm\). Biết khoảng cách giữa hai nguồn là \( d = 2\;mm \) và khoảng cách từ hai nguồn đến màn quan sát là \( D = 1\;m \). Hãy tính hiệu số đường đi \( \Delta l \) của sóng tại một điểm M trên màn quan sát, cách vân trung tâm một khoảng \( x = 0.3\;mm \).
Lời giải:
- Trước tiên, ta sử dụng công thức tính vị trí vân sáng thứ \( k \) trong giao thoa ánh sáng:
\[
x_k = k \cdot \frac{\lambda D}{d}
\]
Trong đó:
- \( x_k \): vị trí của vân sáng thứ \( k \)
- \( \lambda \): bước sóng ánh sáng
- \( D \): khoảng cách từ hai khe đến màn quan sát
- \( d \): khoảng cách giữa hai khe
- Hiệu số đường đi \( \Delta l \) giữa hai sóng từ \( S_1 \) và \( S_2 \) tại điểm M là: \[ \Delta l = \frac{x \cdot d}{D} \]
- Thay các giá trị vào: \[ \Delta l = \frac{0.3 \times 10^{-3} \cdot 2 \times 10^{-3}}{1} = 6 \times 10^{-7}\;m = 600\;nm \] Do đó, tại điểm M, hiệu số đường đi của sóng là \( \Delta l = 600\;nm \).
- Điểm M tương ứng với vân sáng bậc \( k = 1 \) vì \( \Delta l = k \cdot \lambda \), với \( k = 1 \).
Như vậy, ta đã xác định được hiệu số đường đi của sóng tại điểm M trên màn quan sát và biết rằng M nằm trên vân sáng bậc 1.
Bài Tập 10: Bài Tập Tổng Hợp Về Giao Thoa Ánh Sáng
Trong bài tập này, chúng ta sẽ tiến hành tổng hợp kiến thức về giao thoa ánh sáng qua một số bài tập liên quan đến các hiện tượng giao thoa trong thí nghiệm Young. Đây là cơ hội tốt để bạn củng cố kiến thức và rèn luyện kỹ năng giải bài tập về giao thoa ánh sáng.
- Bài toán 1: Xác định bước sóng \( \lambda \) của ánh sáng trong thí nghiệm Young với các điều kiện sau:
- Khoảng cách giữa hai khe \( a = 0.5 \, mm \).
- Khoảng cách từ hai khe đến màn \( D = 2 \, m \).
- Khoảng cách giữa hai vân sáng bậc 10 và vân sáng trung tâm là \( 2.5 \, cm \).
- Bài toán 2: Trong thí nghiệm Young, xác định số vân sáng quan sát được trên màn với các điều kiện:
- Khoảng cách giữa hai khe \( a = 1 \, mm \).
- Khoảng cách từ hai khe đến màn \( D = 1.5 \, m \).
- Bước sóng ánh sáng \( \lambda = 600 \, nm \).
- Chiều dài màn là \( 20 \, cm \).
- Bài toán 3: Tính khoảng cách từ vân sáng bậc 4 đến vân tối bậc 3 trong thí nghiệm giao thoa ánh sáng đơn sắc.
- Bước sóng ánh sáng \( \lambda = 500 \, nm \).
- Khoảng cách giữa hai khe \( a = 0.8 \, mm \).
- Khoảng cách từ hai khe đến màn \( D = 2 \, m \).
- Bài toán 4: Xác định vị trí vân sáng bậc 6 trong thí nghiệm giao thoa với ánh sáng đơn sắc có bước sóng \( \lambda = 700 \, nm \).
- Khoảng cách giữa hai khe \( a = 0.6 \, mm \).
- Khoảng cách từ hai khe đến màn \( D = 1.8 \, m \).
Lời giải:
Từ dữ liệu đã cho, ta áp dụng công thức tính khoảng vân \( i \) như sau:
\[ i = \frac{\lambda D}{a} \]Khi đó, khoảng cách từ vân sáng bậc 10 đến vân trung tâm là:
\[ x_{10} = 10i \]Giải phương trình:
\[ 2.5 \times 10^{-2} = 10 \times \frac{\lambda \times 2}{0.5 \times 10^{-3}} \]Suy ra \( \lambda = 625 \, nm \).
Lời giải:
Đầu tiên, tính khoảng vân \( i \):
\[ i = \frac{\lambda D}{a} = \frac{600 \times 10^{-9} \times 1.5}{1 \times 10^{-3}} = 0.9 \, mm \]Số vân sáng trên màn được tính theo công thức:
\[ N = \frac{L}{i} = \frac{200}{0.9} \approx 222 \, vânLời giải:
Khi đó, ta tính khoảng vân \( i \) như sau:
\[ i = \frac{\lambda D}{a} = \frac{500 \times 10^{-9} \times 2}{0.8 \times 10^{-3}} = 1.25 \, mm \]Khoảng cách từ vân sáng bậc 4 đến vân tối bậc 3 là:
\[ x = (4 - 3) \times i = 1.25 \, mm \]Lời giải:
Sử dụng công thức:
\[ i = \frac{\lambda D}{a} = \frac{700 \times 10^{-9} \times 1.8}{0.6 \times 10^{-3}} = 2.1 \, mm \]Vị trí vân sáng bậc 6 là:
\[ x_6 = 6i = 12.6 \, mm