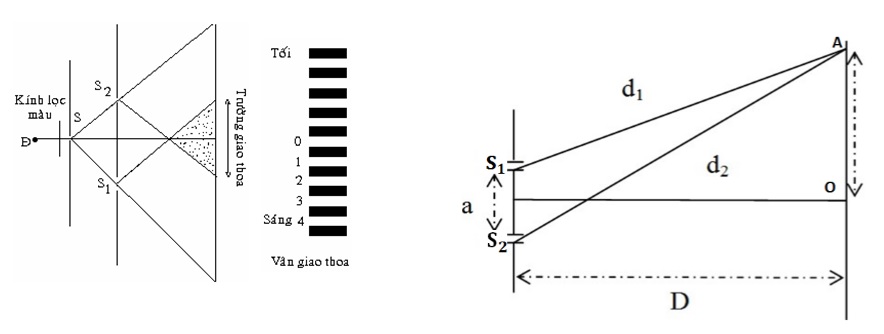
Chủ đề khoảng vân giao thoa: Khoảng vân giao thoa là một hiện tượng quang học quan trọng, thường xuất hiện trong các thí nghiệm vật lý. Bài viết này sẽ giúp bạn khám phá chi tiết về khái niệm, công thức tính toán, và những ứng dụng thực tiễn của khoảng vân giao thoa trong đời sống và công nghệ.
Mục lục
Khoảng Vân Giao Thoa
Khoảng vân giao thoa là một hiện tượng quang học quan trọng trong nghiên cứu về sóng ánh sáng. Nó xảy ra khi hai chùm sáng từ hai khe hẹp giao thoa với nhau và tạo ra các vân sáng và tối trên màn quan sát. Hiện tượng này được sử dụng rộng rãi trong các thí nghiệm vật lý để nghiên cứu tính chất của ánh sáng và ứng dụng trong nhiều lĩnh vực khác nhau.
Công Thức Tính Khoảng Vân
Công thức cơ bản để tính khoảng vân (\(i\)) trong thí nghiệm khe Young là:
\[
i = \frac{\lambda \cdot D}{a}
\]
trong đó:
- \(\lambda\) là bước sóng của ánh sáng (đơn vị: mét).
- D là khoảng cách từ mặt phẳng chứa hai khe đến màn quan sát (đơn vị: mét).
- a là khoảng cách giữa hai khe (đơn vị: mét).
Yếu Tố Ảnh Hưởng Đến Khoảng Vân
Kích thước của khoảng vân phụ thuộc vào một số yếu tố chính sau:
- Bước sóng ánh sáng (\(\lambda\)): Khoảng vân tăng khi bước sóng ánh sáng tăng.
- Khoảng cách từ khe đến màn (D): Khoảng vân tăng khi khoảng cách D tăng.
- Khoảng cách giữa hai khe (a): Khoảng vân giảm khi khoảng cách giữa hai khe tăng.
- Môi trường truyền: Sự thay đổi chiết suất của môi trường sẽ làm thay đổi kích thước khoảng vân.
Ứng Dụng Thực Tế
Khoảng vân giao thoa không chỉ là một hiện tượng lý thuyết mà còn có nhiều ứng dụng quan trọng trong đời sống và khoa học:
- Đo lường 3D và hồ sơ học: Công nghệ chiếu sọc fringe được sử dụng rộng rãi trong đo lường 3D và profilometry để xác định hình dạng và độ sâu của đối tượng.
- Y học: Trong y học, kỹ thuật giao thoa ánh sáng được sử dụng để cải thiện độ phân giải hình ảnh trong siêu âm và MRI, giúp chẩn đoán chính xác hơn.
- Nghiên cứu vật liệu: Kỹ thuật fringe như moiré fringe được áp dụng để nghiên cứu các đặc tính cơ học của vật liệu.
- Khảo sát địa chất: Trong khảo sát địa chất, khoảng vân được sử dụng để phân tích sự di chuyển của tấm kiến tạo và đánh giá các rủi ro động đất.
Kết Luận
Hiện tượng giao thoa và khoảng vân giao thoa là những khái niệm quan trọng trong quang học và có nhiều ứng dụng trong khoa học và công nghệ. Hiểu rõ về chúng giúp nâng cao hiệu quả trong nghiên cứu và ứng dụng thực tiễn, từ y học đến công nghệ sản xuất.
.png)
1. Giới thiệu về Khoảng Vân Giao Thoa
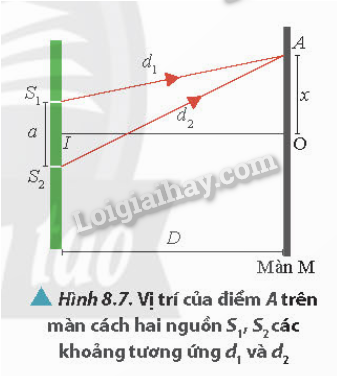
Khoảng vân giao thoa là hiện tượng quang học quan trọng được phát hiện từ việc quan sát sự giao thoa của các sóng ánh sáng. Khi hai hoặc nhiều sóng ánh sáng kết hợp với nhau, chúng tạo ra các vân sáng và tối trên màn quan sát, gọi là các vân giao thoa. Khoảng cách giữa hai vân sáng (hoặc hai vân tối) liên tiếp được gọi là khoảng vân.
Công thức tính khoảng vân \(i\) được xác định bằng:
Trong đó:
- \(\lambda\): Bước sóng của ánh sáng.
- \(D\): Khoảng cách từ màn đến nguồn sáng.
- \(a\): Khoảng cách giữa hai khe sáng.
Khoảng vân giao thoa là một trong những hiện tượng quan trọng trong vật lý quang học, và nó có ứng dụng rộng rãi trong nhiều lĩnh vực như y học, công nghệ, và viễn thông.
2. Ứng dụng của Khoảng Vân Giao Thoa
Khoảng vân giao thoa, một hiện tượng quang học đặc trưng, có nhiều ứng dụng quan trọng trong các lĩnh vực khác nhau. Dưới đây là một số ứng dụng nổi bật của hiện tượng này:
- Trong Y học: Khoảng vân giao thoa được sử dụng trong các kỹ thuật hình ảnh y tế, như chụp cắt lớp giao thoa quang học (OCT). Kỹ thuật này cho phép tạo ra hình ảnh chi tiết của các mô sinh học, hỗ trợ chẩn đoán và theo dõi bệnh tật.
- Trong Công nghệ: Giao thoa ánh sáng được áp dụng trong sản xuất các thiết bị quang học chính xác như gương, lăng kính, và các hệ thống laser. Đo lường và điều chỉnh khoảng vân giúp đảm bảo chất lượng và độ chính xác của các sản phẩm này.
- Trong Viễn thông: Hiện tượng giao thoa được sử dụng trong công nghệ truyền dẫn quang học, giúp tăng cường độ chính xác và hiệu quả của việc truyền tín hiệu qua sợi quang. Điều này đóng vai trò quan trọng trong việc phát triển các hệ thống truyền thông tốc độ cao.
- Trong Nghiên cứu Khoa học: Khoảng vân giao thoa là một công cụ quan trọng trong nghiên cứu vật lý và quang học. Nó giúp các nhà khoa học hiểu rõ hơn về tính chất của ánh sáng và sự tương tác giữa các sóng ánh sáng.

3. Phân tích lý thuyết về Giao Thoa Ánh Sáng
Giao thoa ánh sáng là hiện tượng khi hai hay nhiều sóng ánh sáng kết hợp với nhau, tạo ra sự chồng lấp, dẫn đến xuất hiện các vân sáng và tối trên màn ảnh. Để hiểu rõ hiện tượng này, cần phân tích chi tiết các yếu tố lý thuyết liên quan:
- Bản chất sóng của ánh sáng: Ánh sáng có tính chất của sóng, và mỗi chùm sáng có thể được mô tả bằng các sóng với các bước sóng nhất định. Khi hai sóng ánh sáng gặp nhau, chúng có thể giao thoa, tạo ra các vùng có cường độ ánh sáng khác nhau.
- Điều kiện giao thoa: Để hiện tượng giao thoa xảy ra, các sóng ánh sáng phải có cùng bước sóng và phải có sự lệch pha ổn định. Điều này thường được thực hiện bằng cách sử dụng nguồn sáng đơn sắc và hai khe hẹp trong thí nghiệm giao thoa Young.
- Phân tích toán học: Khi hai sóng ánh sáng gặp nhau, tổng cường độ ánh sáng tại một điểm trên màn sẽ được tính bằng phương trình tổng của hai sóng: \[ I = I_1 + I_2 + 2\sqrt{I_1I_2}\cos(\Delta \phi) \] Trong đó \(I_1\) và \(I_2\) là cường độ của hai sóng, và \(\Delta \phi\) là độ lệch pha giữa chúng.
- Khoảng vân: Khoảng vân là khoảng cách giữa hai vân sáng liên tiếp hoặc hai vân tối liên tiếp. Công thức tính khoảng vân:
\[
i = \frac{\lambda D}{a}
\]
Trong đó:
- \(\lambda\): Bước sóng của ánh sáng
- \(D\): Khoảng cách từ màn đến hai khe
- \(a\): Khoảng cách giữa hai khe
Như vậy, hiện tượng giao thoa ánh sáng không chỉ giúp chúng ta hiểu rõ hơn về bản chất của ánh sáng mà còn có nhiều ứng dụng quan trọng trong các lĩnh vực khoa học và công nghệ.

4. Bài Tập Về Khoảng Vân Giao Thoa
Dưới đây là một số bài tập về khoảng vân giao thoa giúp bạn hiểu rõ hơn về hiện tượng giao thoa ánh sáng và cách tính toán khoảng vân.
- Bài tập 1: Trong một thí nghiệm Young, khoảng cách giữa hai khe là \(a = 0.5\) mm, khoảng cách từ hai khe đến màn quan sát là \(D = 2\) m, ánh sáng sử dụng có bước sóng \(\lambda = 600\) nm. Tính khoảng vân \(i\).
- Giải: Sử dụng công thức: \[ i = \frac{\lambda D}{a} = \frac{600 \times 10^{-9} \times 2}{0.5 \times 10^{-3}} = 2.4 \, \text{mm} \]
- Bài tập 2: Thí nghiệm giao thoa ánh sáng sử dụng ánh sáng đơn sắc có bước sóng \( \lambda = 700 \) nm. Nếu khoảng cách giữa hai khe là \(a = 0.6\) mm và khoảng cách từ hai khe đến màn quan sát là \(D = 1.5\) m, tính khoảng vân.
- Giải: Sử dụng công thức khoảng vân: \[ i = \frac{\lambda D}{a} = \frac{700 \times 10^{-9} \times 1.5}{0.6 \times 10^{-3}} = 1.75 \, \text{mm} \]
- Bài tập 3: Trong một thí nghiệm Young, khoảng cách giữa hai khe là \(0.4\) mm và khoảng cách từ hai khe đến màn là \(2.5\) m. Ánh sáng đơn sắc có bước sóng \(500\) nm được sử dụng. Tính khoảng vân.
- Giải: Công thức khoảng vân: \[ i = \frac{\lambda D}{a} = \frac{500 \times 10^{-9} \times 2.5}{0.4 \times 10^{-3}} = 3.125 \, \text{mm} \]
- Bài tập 4: Trong một thí nghiệm giao thoa ánh sáng, nếu thay đổi khoảng cách từ hai khe đến màn từ 2 m xuống 1.5 m, trong khi giữ nguyên khoảng cách giữa hai khe và bước sóng của ánh sáng, tính tỉ lệ thay đổi của khoảng vân.
- Giải: Tỉ lệ thay đổi của khoảng vân là: \[ \frac{i_2}{i_1} = \frac{D_2}{D_1} = \frac{1.5}{2} = 0.75 \]
- Bài tập 5: Ánh sáng có bước sóng \( \lambda = 550 \) nm được sử dụng trong một thí nghiệm Young, với khoảng cách giữa hai khe là \(0.3\) mm và khoảng cách từ hai khe đến màn là \(2\) m. Tính khoảng vân.
- Giải: Sử dụng công thức khoảng vân: \[ i = \frac{\lambda D}{a} = \frac{550 \times 10^{-9} \times 2}{0.3 \times 10^{-3}} = 3.67 \, \text{mm} \]
- Bài tập 6: Nếu bước sóng của ánh sáng sử dụng trong thí nghiệm tăng lên gấp đôi, trong khi các điều kiện khác không thay đổi, khoảng vân sẽ thay đổi như thế nào?
- Giải: Khoảng vân sẽ tăng gấp đôi, vì \( i \propto \lambda \).
- Bài tập 7: Trong một thí nghiệm, ánh sáng có bước sóng \( \lambda = 450 \) nm được sử dụng, với khoảng cách giữa hai khe là \(0.25\) mm và khoảng cách từ hai khe đến màn là \(1.8\) m. Tính khoảng vân.
- Giải: Sử dụng công thức khoảng vân: \[ i = \frac{\lambda D}{a} = \frac{450 \times 10^{-9} \times 1.8}{0.25 \times 10^{-3}} = 3.24 \, \text{mm} \]
- Bài tập 8: Nếu khoảng cách giữa hai khe trong thí nghiệm Young được giảm đi một nửa, trong khi các điều kiện khác không đổi, tính sự thay đổi của khoảng vân.
- Giải: Khoảng vân sẽ tăng gấp đôi, vì \( i \propto \frac{1}{a} \).
- Bài tập 9: Trong một thí nghiệm, nếu khoảng cách từ hai khe đến màn giảm một nửa, bước sóng ánh sáng và khoảng cách giữa hai khe không thay đổi, khoảng vân sẽ thay đổi như thế nào?
- Giải: Khoảng vân sẽ giảm một nửa, vì \( i \propto D \).
- Bài tập 10: Tính khoảng vân trong thí nghiệm Young với dữ liệu sau: ánh sáng có bước sóng \( \lambda = 650 \) nm, khoảng cách giữa hai khe là \(0.45\) mm, khoảng cách từ hai khe đến màn là \(2.2\) m.
- Giải: Sử dụng công thức khoảng vân: \[ i = \frac{\lambda D}{a} = \frac{650 \times 10^{-9} \times 2.2}{0.45 \times 10^{-3}} = 3.18 \, \text{mm} \]