Chủ đề lý 11 giao thoa sóng: Bài viết này cung cấp một cái nhìn toàn diện về chủ đề "Lý 11 Giao Thoa Sóng", bao gồm các khái niệm cơ bản, công thức quan trọng, và ứng dụng thực tế. Được thiết kế dành cho học sinh và người học, bài viết giúp nắm vững lý thuyết và cách giải quyết các dạng bài tập phổ biến về giao thoa sóng.
Mục lục
- Khái niệm về giao thoa sóng
- Công thức tính giao thoa sóng
- Thí nghiệm giao thoa sóng
- Kết luận
- Công thức tính giao thoa sóng
- Thí nghiệm giao thoa sóng
- Kết luận
- Thí nghiệm giao thoa sóng
- Kết luận
- Kết luận
- 1. Khái niệm cơ bản về giao thoa sóng
- 2. Công thức và phương trình trong giao thoa sóng
- 3. Ứng dụng của giao thoa sóng trong đời sống
- 4. Các dạng bài tập giao thoa sóng
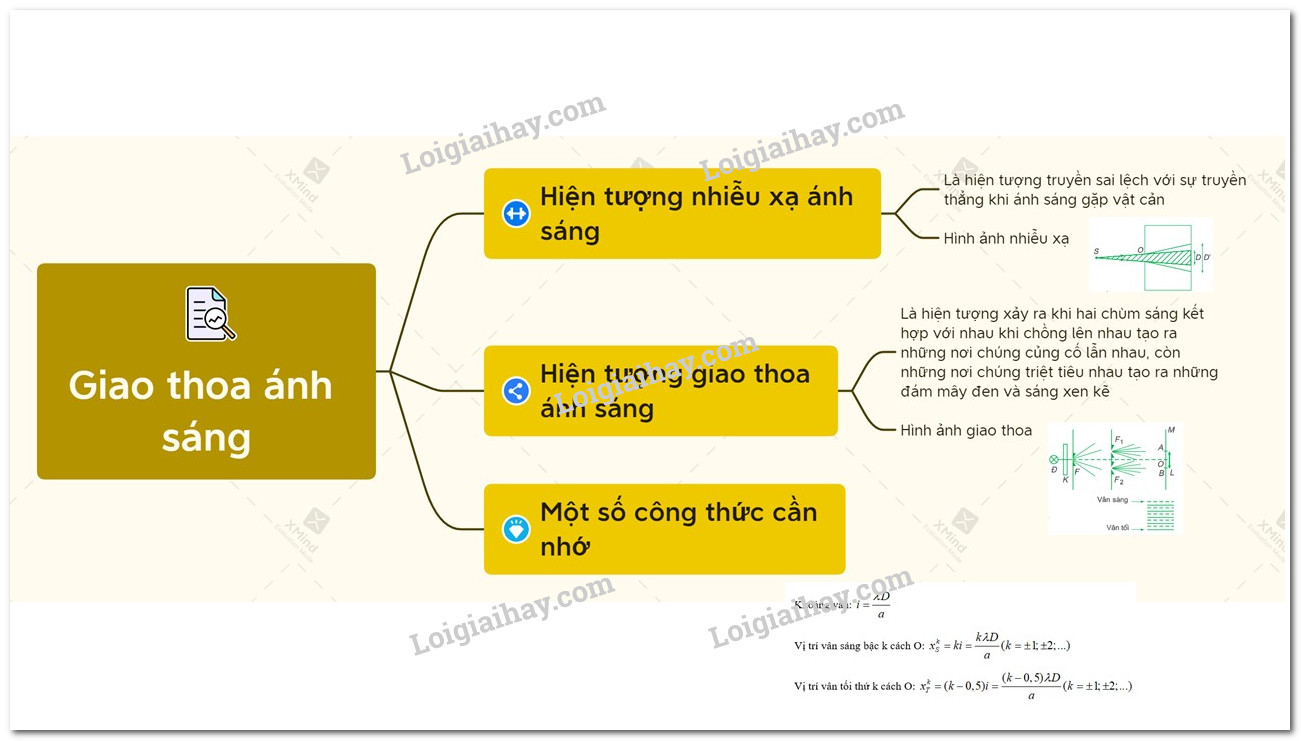
Khái niệm về giao thoa sóng
Giao thoa sóng là hiện tượng xảy ra khi hai hay nhiều sóng kết hợp gặp nhau, tạo ra những vùng có biên độ dao động cực đại và những vùng có biên độ dao động cực tiểu. Đây là một trong những hiện tượng đặc trưng trong sóng cơ học và được áp dụng rộng rãi trong các lĩnh vực khoa học và kỹ thuật.

.png)
Công thức tính giao thoa sóng
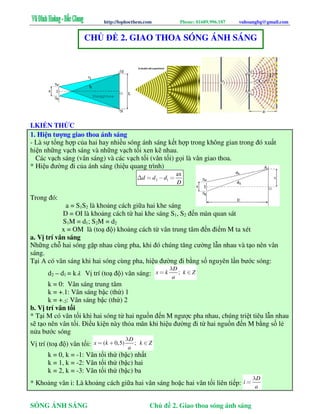
Trong hiện tượng giao thoa sóng, vị trí của các cực đại và cực tiểu có thể được xác định bằng các công thức sau:
- Vị trí cực đại giao thoa: \[d_2 - d_1 = k\lambda\]
- Vị trí cực tiểu giao thoa: \[d_2 - d_1 = \left(k + \frac{1}{2}\right)\lambda\]
- Công thức tính bước sóng: \[\lambda = \frac{v}{f}\]
- Khoảng vân giao thoa: \[i = \frac{\lambda D}{a}\]
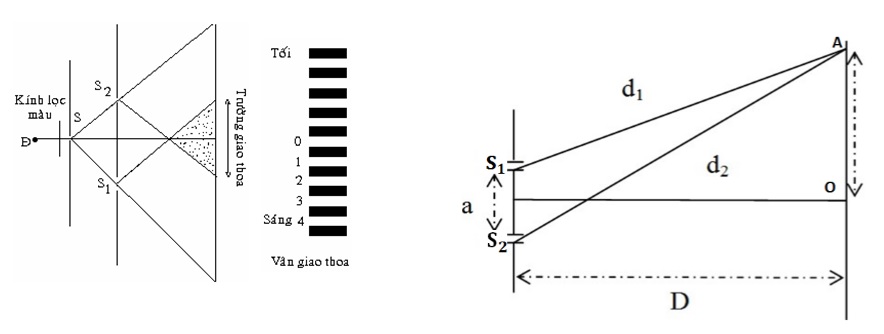
Thí nghiệm giao thoa sóng
Thí nghiệm giao thoa sóng có thể được thực hiện trên mặt nước bằng cách sử dụng hai nguồn phát sóng dao động cùng tần số và cùng pha. Khi đó, trên mặt nước sẽ xuất hiện các vân giao thoa là các đường giao nhau giữa hai sóng.
Ví dụ minh họa
Giả sử hai nguồn phát sóng A và B dao động cùng pha với tần số \(f = 50Hz\) và cách nhau một khoảng \(a = 5cm\). Bước sóng của sóng là \( \lambda = 1cm \). Khi đó, khoảng vân giao thoa trên màn quan sát là:
\[i = \frac{\lambda D}{a} = \frac{1 \times 100}{5} = 20cm\]

Kết luận
Hiện tượng giao thoa sóng là một minh chứng rõ ràng cho tính chất giao thoa của sóng cơ học, giúp chúng ta hiểu rõ hơn về bản chất của sóng và các ứng dụng thực tiễn trong khoa học kỹ thuật.

Công thức tính giao thoa sóng
Trong hiện tượng giao thoa sóng, vị trí của các cực đại và cực tiểu có thể được xác định bằng các công thức sau:
- Vị trí cực đại giao thoa: \[d_2 - d_1 = k\lambda\]
- Vị trí cực tiểu giao thoa: \[d_2 - d_1 = \left(k + \frac{1}{2}\right)\lambda\]
- Công thức tính bước sóng: \[\lambda = \frac{v}{f}\]
- Khoảng vân giao thoa: \[i = \frac{\lambda D}{a}\]

Thí nghiệm giao thoa sóng
Thí nghiệm giao thoa sóng có thể được thực hiện trên mặt nước bằng cách sử dụng hai nguồn phát sóng dao động cùng tần số và cùng pha. Khi đó, trên mặt nước sẽ xuất hiện các vân giao thoa là các đường giao nhau giữa hai sóng.
Ví dụ minh họa
Giả sử hai nguồn phát sóng A và B dao động cùng pha với tần số \(f = 50Hz\) và cách nhau một khoảng \(a = 5cm\). Bước sóng của sóng là \( \lambda = 1cm \). Khi đó, khoảng vân giao thoa trên màn quan sát là:
\[i = \frac{\lambda D}{a} = \frac{1 \times 100}{5} = 20cm\]
XEM THÊM:
Kết luận
Hiện tượng giao thoa sóng là một minh chứng rõ ràng cho tính chất giao thoa của sóng cơ học, giúp chúng ta hiểu rõ hơn về bản chất của sóng và các ứng dụng thực tiễn trong khoa học kỹ thuật.

Thí nghiệm giao thoa sóng
Thí nghiệm giao thoa sóng có thể được thực hiện trên mặt nước bằng cách sử dụng hai nguồn phát sóng dao động cùng tần số và cùng pha. Khi đó, trên mặt nước sẽ xuất hiện các vân giao thoa là các đường giao nhau giữa hai sóng.
Ví dụ minh họa
Giả sử hai nguồn phát sóng A và B dao động cùng pha với tần số \(f = 50Hz\) và cách nhau một khoảng \(a = 5cm\). Bước sóng của sóng là \( \lambda = 1cm \). Khi đó, khoảng vân giao thoa trên màn quan sát là:
\[i = \frac{\lambda D}{a} = \frac{1 \times 100}{5} = 20cm\]

Kết luận
Hiện tượng giao thoa sóng là một minh chứng rõ ràng cho tính chất giao thoa của sóng cơ học, giúp chúng ta hiểu rõ hơn về bản chất của sóng và các ứng dụng thực tiễn trong khoa học kỹ thuật.
Kết luận
Hiện tượng giao thoa sóng là một minh chứng rõ ràng cho tính chất giao thoa của sóng cơ học, giúp chúng ta hiểu rõ hơn về bản chất của sóng và các ứng dụng thực tiễn trong khoa học kỹ thuật.

1. Khái niệm cơ bản về giao thoa sóng
Giao thoa sóng là hiện tượng quan trọng trong vật lý sóng, khi hai hay nhiều sóng gặp nhau tại cùng một điểm trong không gian. Khi đó, các sóng này sẽ kết hợp với nhau, tạo ra một sóng mới với biên độ phụ thuộc vào sự giao thoa của các sóng gốc.
- Điều kiện giao thoa sóng: Để xảy ra giao thoa, hai nguồn sóng phải là nguồn kết hợp, tức là có cùng tần số và có hiệu số pha không đổi theo thời gian.
- Sóng kết hợp: Là các sóng có cùng tần số và hiệu số pha không đổi, thường đến từ các nguồn sóng đồng bộ hoặc đồng pha.
- Hiện tượng giao thoa: Khi hai sóng kết hợp gặp nhau, tại các điểm mà hai sóng có cùng pha, biên độ tổng hợp sẽ tăng lên, tạo ra cực đại giao thoa. Ngược lại, tại các điểm mà hai sóng ngược pha, biên độ tổng hợp sẽ giảm xuống, tạo ra cực tiểu giao thoa.
Các cực đại giao thoa xuất hiện khi hiệu đường đi của hai sóng từ hai nguồn đến một điểm bằng bội số nguyên của bước sóng, tức là:
Trong khi đó, các cực tiểu giao thoa xuất hiện khi hiệu đường đi bằng một số lẻ của nửa bước sóng, tức là:
2. Công thức và phương trình trong giao thoa sóng
Trong hiện tượng giao thoa sóng, các công thức và phương trình đóng vai trò quan trọng trong việc xác định các điểm cực đại và cực tiểu giao thoa, cũng như tính toán biên độ tổng hợp của sóng tại một điểm. Dưới đây là các công thức cơ bản và phương trình liên quan đến giao thoa sóng:
- Phương trình sóng tổng hợp: Khi hai sóng gặp nhau, phương trình sóng tổng hợp tại một điểm là:
Trong đó:
- \(u_1\), \(u_2\) là phương trình của hai sóng thành phần.
- \(A_1\), \(A_2\) là biên độ của hai sóng.
- \(\varphi_1\), \(\varphi_2\) là pha ban đầu của hai sóng.
Khi hai sóng có cùng biên độ \(A\) và cùng tần số \(\omega\), phương trình sóng tổng hợp sẽ là:
Với \(\Delta \varphi = \varphi_2 - \varphi_1\) là hiệu pha của hai sóng.
- Cực đại giao thoa: Các điểm cực đại giao thoa xuất hiện tại các vị trí mà hiệu đường đi của hai sóng từ hai nguồn đến một điểm bằng bội số nguyên của bước sóng:
- Cực tiểu giao thoa: Các điểm cực tiểu giao thoa xuất hiện tại các vị trí mà hiệu đường đi bằng một số lẻ của nửa bước sóng:
Những công thức trên là nền tảng để giải quyết các bài toán về giao thoa sóng, giúp xác định vị trí và biên độ của sóng tổng hợp tại các điểm khác nhau trong không gian.
3. Ứng dụng của giao thoa sóng trong đời sống
Giao thoa sóng không chỉ là một hiện tượng vật lý quan trọng trong lý thuyết, mà còn có nhiều ứng dụng thực tế trong đời sống hàng ngày và công nghệ hiện đại. Dưới đây là một số ứng dụng tiêu biểu của giao thoa sóng:
- Ứng dụng trong công nghệ đo lường: Giao thoa kế là thiết bị sử dụng hiện tượng giao thoa để đo khoảng cách, độ dày, và sự thay đổi vị trí với độ chính xác cao, đặc biệt là trong các nghiên cứu vật liệu và các hệ thống quang học.
- Ứng dụng trong viễn thông: Nguyên lý giao thoa sóng được sử dụng trong các hệ thống viễn thông như truyền tín hiệu qua cáp quang. Tín hiệu ánh sáng truyền qua cáp quang sử dụng hiện tượng giao thoa để giảm nhiễu và tăng cường độ tín hiệu, giúp truyền thông tin hiệu quả hơn.
- Ứng dụng trong hình ảnh y khoa: Kỹ thuật chụp ảnh giao thoa kế (Interferometric Imaging) được sử dụng để tạo ra hình ảnh với độ phân giải cao, hỗ trợ trong việc chẩn đoán bệnh tật qua hình ảnh y khoa như chụp cắt lớp quang học (OCT).
- Ứng dụng trong âm học: Hiện tượng giao thoa sóng âm được sử dụng trong thiết kế phòng thu âm, nhà hát, và các không gian âm học khác để kiểm soát và tối ưu hóa âm thanh, giảm thiểu hiện tượng dội âm không mong muốn.
- Ứng dụng trong thiên văn học: Giao thoa sóng được ứng dụng trong giao thoa kế vô tuyến (radio interferometry) để quan sát các đối tượng trong không gian với độ phân giải cao, cho phép các nhà thiên văn học nghiên cứu chi tiết các vật thể vũ trụ như các ngôi sao và hành tinh.
Những ứng dụng trên cho thấy giao thoa sóng là một hiện tượng có giá trị lớn trong nhiều lĩnh vực, từ khoa học cơ bản đến các công nghệ tiên tiến, góp phần nâng cao chất lượng cuộc sống và sự hiểu biết của con người về thế giới xung quanh.

4. Các dạng bài tập giao thoa sóng
Các dạng bài tập về giao thoa sóng trong chương trình Lý 11 rất đa dạng, giúp học sinh nắm vững kiến thức và áp dụng vào thực tế. Dưới đây là một số dạng bài tập cơ bản thường gặp trong đề thi và kiểm tra:
- Dạng 1: Tính toán khoảng vân giao thoa
Trong dạng này, học sinh cần áp dụng công thức tính khoảng vân \(i\) như sau:
\[ i = \frac{\lambda \cdot D}{a} \]với \(\lambda\) là bước sóng, \(D\) là khoảng cách từ nguồn đến màn, và \(a\) là khoảng cách giữa hai nguồn sóng.
- Dạng 2: Xác định vị trí các điểm dao động cực đại và cực tiểu
Bài tập yêu cầu tính toán vị trí \(x\) của các điểm dao động cực đại và cực tiểu trên màn theo công thức:
\[ x = k \cdot i \]với \(k\) là số nguyên xác định cực đại (khi \(k\) là số chẵn) hoặc cực tiểu (khi \(k\) là số lẻ).
- Dạng 3: Tính số cực đại, cực tiểu giữa hai điểm
Dạng này yêu cầu học sinh tính số lượng các điểm cực đại và cực tiểu giữa hai vị trí \(x_1\) và \(x_2\) theo công thức:
\[ N = \frac{x_2 - x_1}{i} \] - Dạng 4: Xác định bước sóng từ các dữ liệu thực nghiệm
Học sinh cần sử dụng dữ liệu về khoảng cách giữa các vân và khoảng cách giữa các nguồn sóng để tính toán bước sóng \(\lambda\).
- Dạng 5: Bài toán về giao thoa của hai sóng âm
Dạng bài này liên quan đến giao thoa sóng âm, yêu cầu xác định các điểm mà sóng âm có cường độ lớn nhất hoặc nhỏ nhất.
- Dạng 6: Bài tập về giao thoa sóng ánh sáng
Trong dạng này, học sinh cần giải các bài toán liên quan đến thí nghiệm Young về giao thoa ánh sáng, tính khoảng cách giữa các vân sáng và tối.
- Dạng 7: Giao thoa sóng trong bể nước
Dạng bài tập này thường liên quan đến việc xác định các vị trí dao động mạnh và yếu trong bể nước khi có giao thoa sóng.
- Dạng 8: Tính tần số của sóng từ hiện tượng giao thoa
Bài tập yêu cầu tính toán tần số của sóng dựa trên các dữ liệu về khoảng cách vân và tốc độ truyền sóng.
- Dạng 9: Xác định vận tốc của sóng từ hiện tượng giao thoa
Dạng này yêu cầu học sinh sử dụng công thức \(v = \lambda \cdot f\) để tính toán vận tốc của sóng từ các thông tin về bước sóng và tần số.
- Dạng 10: Bài tập kết hợp giao thoa và hiện tượng nhiễu xạ
Học sinh cần phân tích và giải quyết các bài toán phức tạp có sự kết hợp giữa giao thoa và nhiễu xạ sóng.