Vân Giao Thoa: Hiện Tượng Sóng và Ứng Dụng Thực Tiễn

Vân giao thoa là một hiện tượng vật lý quan trọng trong nghiên cứu về sóng ánh sáng và sóng âm. Hiện tượng này xảy ra khi hai hoặc nhiều sóng gặp nhau và tương tác với nhau, tạo ra những vùng có cường độ sóng mạnh hơn hoặc yếu hơn. Các vân giao thoa được thể hiện qua các vùng sáng và tối xen kẽ nhau trong thí nghiệm giao thoa ánh sáng hoặc âm thanh.

Khái Niệm Về Giao Thoa

Giao thoa là hiện tượng xảy ra khi hai hay nhiều sóng gặp nhau, và tại các điểm giao thoa, chúng có thể tăng cường hoặc triệt tiêu lẫn nhau. Hiện tượng này được ứng dụng rộng rãi trong các lĩnh vực khoa học và công nghệ, đặc biệt trong quang học, âm học, và truyền thông.

Điều Kiện Hình Thành Vân Giao Thoa

• Hai nguồn sóng phải có cùng tần số và có độ lệch pha không đổi theo thời gian.
• Các sóng phải gặp nhau trong môi trường đồng nhất.
• Khoảng cách giữa các vân sáng và vân tối được xác định bởi bước sóng và khoảng cách giữa hai nguồn sóng.

Công Thức Tính Vị Trí Vân Sáng và Vân Tối

Vị trí của các vân sáng và vân tối trong hiện tượng giao thoa có thể được xác định bằng các công thức:

Vị trí vân sáng:

\[
x_n = n\lambda \frac{D}{d}
\]
trong đó:

• \(x_n\) là vị trí vân sáng thứ n
• \(\lambda\) là bước sóng của sóng
• D là khoảng cách từ hai khe đến màn quan sát
• d là khoảng cách giữa hai khe

Vị trí vân tối:

\[
x_n = \left(n + \frac{1}{2}\right)\lambda \frac{D}{d}
\]
trong đó:

• \(x_n\) là vị trí vân tối thứ n
• Các tham số khác tương tự như công thức tính vị trí vân sáng.

Ứng Dụng Của Hiện Tượng Giao Thoa

Hiện tượng giao thoa được ứng dụng trong nhiều lĩnh vực khác nhau, bao gồm:

• Trong quang học, giao thoa ánh sáng được ứng dụng trong kính hiển vi giao thoa, interferometer.
• Trong âm học, giao thoa sóng âm được sử dụng để kiểm tra chất lượng âm thanh và phát triển các hệ thống âm thanh không gian.
• Trong truyền thông, kỹ thuật giao thoa được áp dụng để tăng cường hoặc triệt tiêu tín hiệu, giúp nâng cao chất lượng truyền tải.

Thí Nghiệm Giao Thoa Nổi Tiếng

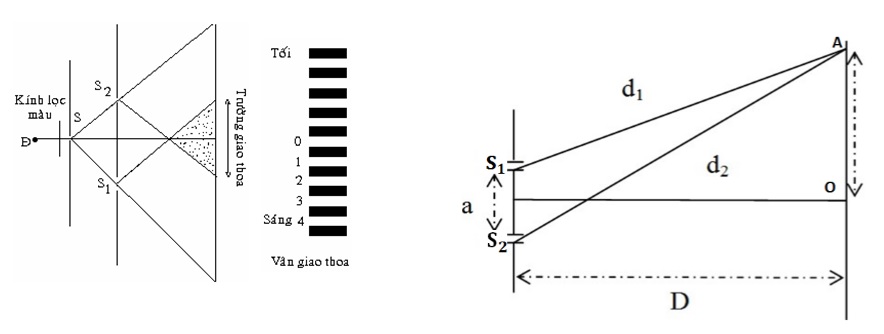
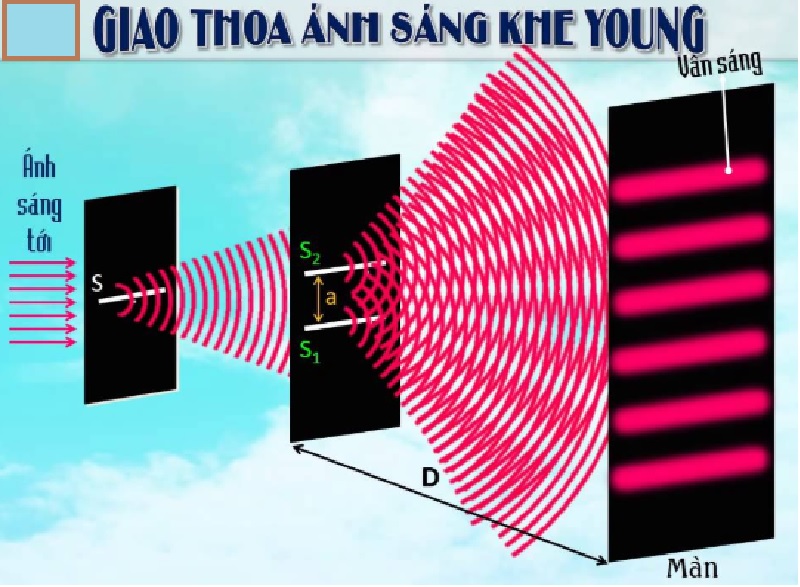
Thí nghiệm Young về giao thoa ánh sáng là một trong những thí nghiệm nổi tiếng nhất, minh chứng cho bản chất sóng của ánh sáng. Trong thí nghiệm này, ánh sáng đi qua hai khe song song, tạo ra các vân giao thoa trên màn quan sát.

Kết Luận

Hiện tượng giao thoa là một trong những minh chứng rõ ràng nhất cho sự tương tác giữa các sóng. Nghiên cứu về hiện tượng này không chỉ mang lại kiến thức quan trọng trong lĩnh vực khoa học cơ bản mà còn mở ra nhiều ứng dụng trong công nghệ hiện đại.

Vân giao thoa là hiện tượng quan trọng trong vật lý sóng, xảy ra khi hai hay nhiều sóng kết hợp giao thoa với nhau, tạo ra các vùng sóng cường độ khác nhau trên màn quan sát. Hiện tượng này được quan sát rõ ràng trong thí nghiệm với ánh sáng đơn sắc qua hai khe hẹp.

Trong thí nghiệm của Thomas Young vào năm 1801, hai chùm sáng từ hai khe hẹp gặp nhau và tạo ra các vân sáng và tối trên màn. Hiện tượng này là do sự chồng chất của sóng ánh sáng từ hai nguồn kết hợp, gây ra sự giao thoa tăng cường hoặc triệt tiêu tại các vị trí khác nhau trên màn.

Các vân sáng được hình thành tại các vị trí mà hai sóng gặp nhau với hiệu số pha bằng bội số nguyên của bước sóng, dẫn đến sự tăng cường lẫn nhau. Ngược lại, các vân tối xuất hiện tại những nơi mà hiệu số pha bằng bội số lẻ của nửa bước sóng, dẫn đến sự triệt tiêu hoàn toàn.

Hiện tượng vân giao thoa có nhiều ứng dụng thực tiễn, từ việc đo lường chính xác các thông số vật lý như bước sóng, đến các công nghệ trong quang học, như kính hiển vi giao thoa và hệ thống đo lường bằng laser.

• Nguyên lý cơ bản: Sóng giao thoa với nhau, tạo ra các vân sáng và tối.
• Ứng dụng: Đo bước sóng, nghiên cứu quang học và phát triển công nghệ.
• Thí nghiệm nổi bật: Thí nghiệm Young với ánh sáng qua hai khe.

Hiện tượng giao thoa ánh sáng xảy ra khi hai hay nhiều sóng ánh sáng gặp nhau và tạo ra các vân sáng và tối do sự chồng chất của sóng. Để hiện tượng giao thoa này xảy ra, cần đảm bảo các điều kiện sau:

• Các nguồn sáng kết hợp: Hai nguồn sáng cần có cùng tần số (hoặc bước sóng) và có sự chênh lệch pha không đổi theo thời gian. Điều này đảm bảo rằng sự giao thoa xảy ra ổn định và tạo ra các vân giao thoa rõ ràng.
• Ánh sáng đơn sắc: Ánh sáng phải đơn sắc, tức là có một bước sóng duy nhất. Nếu sử dụng ánh sáng không đơn sắc, các vân giao thoa sẽ bị mờ đi do các thành phần có bước sóng khác nhau giao thoa với nhau.
• Cùng pha hoặc có sự chênh lệch pha ổn định: Hai sóng ánh sáng cần phải có cùng pha hoặc có sự chênh lệch pha cố định để có thể tạo ra các vùng giao thoa rõ ràng.
• Khoảng cách giữa các khe hẹp: Trong thí nghiệm Young, khoảng cách giữa hai khe phải nhỏ so với khoảng cách từ khe đến màn quan sát để các sóng từ hai khe có thể giao thoa với nhau.
• Môi trường truyền sóng: Sóng ánh sáng cần truyền qua môi trường đồng nhất và không bị biến đổi tính chất trên đường truyền để duy trì sự ổn định của vân giao thoa.

Khi các điều kiện này được đáp ứng, hiện tượng giao thoa ánh sáng sẽ tạo ra các vân sáng và tối trên màn quan sát, phản ánh sự tăng cường và triệt tiêu lẫn nhau của các sóng ánh sáng tại các vị trí khác nhau.

Trong thí nghiệm giao thoa ánh sáng, để xác định vị trí của các vân sáng và vân tối trên màn quan sát, ta sử dụng các công thức sau:

• Vân sáng: Vị trí vân sáng (cực đại giao thoa) được xác định bằng công thức: \[ x_k = \frac{k \cdot \lambda \cdot D}{a} \] Trong đó:
  • \( x_k \): Vị trí vân sáng thứ \( k \) (với \( k = 0, \pm 1, \pm 2, \ldots \))
  • \( \lambda \): Bước sóng của ánh sáng
  • \( D \): Khoảng cách từ hai khe đến màn quan sát
  • \( a \): Khoảng cách giữa hai khe
• Vân tối: Vị trí vân tối (cực tiểu giao thoa) được xác định bằng công thức: \[ x'_k = \frac{(k + 0.5) \cdot \lambda \cdot D}{a} \] Trong đó:
  • \( x'_k \): Vị trí vân tối thứ \( k \) (với \( k = 0, \pm 1, \pm 2, \ldots \))
  • Các ký hiệu còn lại giống với công thức vân sáng.

Bằng cách áp dụng các công thức trên, ta có thể xác định được chính xác vị trí của các vân sáng và vân tối trên màn quan sát, từ đó phân tích và đo lường hiện tượng giao thoa ánh sáng một cách chi tiết.

Khoảng vân giao thoa là khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp trên màn quan sát. Để tính toán khoảng vân giao thoa trong hiện tượng giao thoa ánh sáng, ta sử dụng công thức sau:

Công thức tính khoảng vân giao thoa được xác định như sau:

Trong đó:

• \( i \): Khoảng vân, tức khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp.
• \( \lambda \): Bước sóng của ánh sáng đang sử dụng trong thí nghiệm (đơn vị: mét).
• \( D \): Khoảng cách từ hai khe đến màn quan sát (đơn vị: mét).
• \( a \): Khoảng cách giữa hai khe sáng (đơn vị: mét).

Bằng cách sử dụng công thức trên, ta có thể xác định chính xác khoảng vân giao thoa trong thí nghiệm. Điều này giúp chúng ta hiểu rõ hơn về hiện tượng giao thoa và các yếu tố ảnh hưởng đến sự phân bố của các vân sáng và vân tối.

Hiện tượng giao thoa ánh sáng không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng quan trọng trong thực tế. Dưới đây là một số ứng dụng tiêu biểu:

• Công nghệ đo lường và quang học: Giao thoa ánh sáng được sử dụng trong các thiết bị như máy đo giao thoa kế để đo khoảng cách với độ chính xác cao, kiểm tra bề mặt quang học, và đo sự thay đổi của các vật liệu dưới tác động của nhiệt độ, áp suất.
• Truyền thông quang học: Giao thoa ánh sáng đóng vai trò quan trọng trong các hệ thống truyền thông quang học, đặc biệt trong việc mã hóa và giải mã tín hiệu ánh sáng để truyền dữ liệu với tốc độ cao qua sợi quang.
• Chụp ảnh giao thoa: Kỹ thuật chụp ảnh giao thoa, hay còn gọi là holography, sử dụng hiện tượng giao thoa để tạo ra hình ảnh ba chiều của vật thể, giúp lưu giữ thông tin hình ảnh chi tiết.
• Kiểm tra và đánh giá chất lượng bề mặt: Trong ngành công nghiệp, giao thoa ánh sáng được ứng dụng để kiểm tra và đánh giá độ mịn và độ đồng đều của các bề mặt sản phẩm, chẳng hạn như thấu kính và gương.

Những ứng dụng trên chỉ là một phần nhỏ trong các lĩnh vực mà hiện tượng giao thoa ánh sáng được áp dụng. Nhờ vào sự hiểu biết sâu rộng về hiện tượng này, con người có thể tận dụng ánh sáng để phát triển nhiều công nghệ tiên tiến, phục vụ cho cuộc sống và công nghiệp.

Giao thoa ánh sáng là một hiện tượng quan trọng trong Vật lý, thường xuất hiện trong các bài tập Toán Lý. Dưới đây là một số dạng bài tập phổ biến liên quan đến giao thoa ánh sáng:

• Bài tập tính khoảng vân: Sử dụng công thức tính khoảng vân \[i = \dfrac{\lambda D}{a}\] để xác định khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp.
• Bài tập xác định vị trí vân sáng, vân tối: Tính toán vị trí của các vân sáng và vân tối dựa trên công thức \[x_n = n \cdot \dfrac{\lambda D}{a}\] (vân sáng) và \[x_n = (n + 0.5) \cdot \dfrac{\lambda D}{a}\] (vân tối).
• Bài tập về điều kiện giao thoa: Xác định điều kiện cần thiết để xảy ra giao thoa ánh sáng, bao gồm việc sử dụng nguồn sáng kết hợp và khe hẹp đồng nhất.
• Bài tập phân tích hiện tượng giao thoa: Giải thích các hiện tượng giao thoa trong các thí nghiệm thực tế như thí nghiệm Young.
• Bài tập liên quan đến giao thoa đa sắc: Xác định sự phân tách màu sắc của các vân sáng khi sử dụng ánh sáng đa sắc.
• Bài tập thực hành giao thoa ánh sáng: Xác định các đại lượng thực nghiệm như bước sóng ánh sáng và khoảng cách giữa hai khe.
• Bài tập về sự dịch chuyển vân giao thoa: Tính toán sự thay đổi vị trí của các vân sáng và vân tối khi có sự thay đổi về môi trường hay các điều kiện khác.
• Bài tập về giao thoa của các sóng nước: Áp dụng kiến thức giao thoa ánh sáng vào các bài toán về sóng nước.
• Bài tập kết hợp quang hình và giao thoa: Phân tích các bài toán kết hợp giữa lý thuyết quang hình học và hiện tượng giao thoa ánh sáng.
• Bài tập kiểm tra thực nghiệm: Sử dụng các số liệu từ thí nghiệm để tính toán và dự đoán kết quả của hiện tượng giao thoa.

Việc nắm vững các dạng bài tập này giúp học sinh hiểu rõ hơn về hiện tượng giao thoa ánh sáng và ứng dụng chúng vào việc giải quyết các bài toán liên quan trong chương trình Toán Lý.

Trong bài tập này, chúng ta sẽ tính toán bước sóng của ánh sáng dựa trên dữ liệu về khoảng vân giao thoa, khoảng cách giữa hai khe sáng và khoảng cách từ khe sáng đến màn quan sát.

Đề bài: Một thí nghiệm giao thoa ánh sáng sử dụng hai khe sáng với khoảng cách giữa hai khe là \(a = 0.5 \, mm\), khoảng cách từ hai khe đến màn là \(D = 2 \, m\), khoảng vân giao thoa thu được trên màn là \(i = 1.2 \, mm\). Hãy tính bước sóng \(\lambda\) của ánh sáng được sử dụng.

Hướng dẫn giải:

1. Ta sử dụng công thức tính khoảng vân \(i\) trong hiện tượng giao thoa ánh sáng:

   \[ i = \frac{\lambda D}{a} \]

2. Biến đổi công thức để tính bước sóng \(\lambda\):

   \[ \lambda = \frac{i \times a}{D} \]

3. Thay các giá trị đã cho vào công thức:

   \[ \lambda = \frac{1.2 \times 10^{-3} \times 0.5 \times 10^{-3}}{2} \]

4. Tính toán giá trị:

   \[ \lambda = 3 \times 10^{-7} \, m \]

5. Chuyển đổi đơn vị bước sóng từ mét sang nanomet:

   \[ \lambda = 300 \, nm \]

Kết luận: Bước sóng của ánh sáng trong thí nghiệm này là \(\lambda = 300 \, nm\).

Để tính khoảng cách giữa hai khe trong hiện tượng giao thoa ánh sáng, chúng ta cần áp dụng công thức cơ bản của giao thoa khe đôi. Bài tập này yêu cầu tính toán dựa trên các thông số đã biết như bước sóng của ánh sáng, khoảng cách từ khe đến màn, và vị trí của vân sáng hoặc vân tối.

Công thức giao thoa:

Khoảng cách giữa hai khe \(d\) được tính bằng công thức:

\[
d = \dfrac{\lambda \cdot D}{\Delta x}
\]

• \(\lambda\): Bước sóng ánh sáng chiếu vào khe (m)
• \(D\): Khoảng cách từ hai khe đến màn (m)
• \(\Delta x\): Khoảng cách giữa hai vân sáng liên tiếp hoặc hai vân tối liên tiếp (m)

Ví dụ cụ thể:

1. Cho ánh sáng có bước sóng \(\lambda = 600 nm\), khoảng cách từ khe đến màn \(D = 2 m\), và khoảng cách giữa hai vân sáng liên tiếp \(\Delta x = 0.3 mm\). Hãy tính khoảng cách giữa hai khe.
2. Giải:
3. Trước tiên, đổi đơn vị của các thông số sang hệ mét: \(\lambda = 600 nm = 600 \times 10^{-9} m\), \(\Delta x = 0.3 mm = 0.3 \times 10^{-3} m\).
4. Áp dụng công thức: \(d = \dfrac{\lambda \cdot D}{\Delta x} = \dfrac{600 \times 10^{-9} \cdot 2}{0.3 \times 10^{-3}} = 4 \times 10^{-3} m = 4 mm\).
5. Vậy khoảng cách giữa hai khe là \(d = 4 mm\).

Qua ví dụ này, chúng ta thấy rằng việc áp dụng đúng công thức và quy đổi đơn vị chính xác là rất quan trọng trong việc giải bài tập liên quan đến hiện tượng giao thoa ánh sáng. Hãy thực hành nhiều để nắm vững kỹ năng tính toán này.

Trong các bài tập về giao thoa ánh sáng, việc xác định số vân sáng là một trong những nội dung cơ bản và quan trọng. Để giải quyết bài toán này, ta cần nắm rõ một số công thức và khái niệm sau:

1. Khoảng vân (i): Khoảng cách giữa hai vân sáng liên tiếp, được tính bằng công thức:

   \[ i = \frac{\lambda D}{a} \]

   Trong đó:

   • \(\lambda\) là bước sóng ánh sáng.
   • D là khoảng cách từ hai khe đến màn.
   • a là khoảng cách giữa hai khe.

2. Số vân sáng (N): Số vân sáng có thể quan sát được trên màn, tính theo công thức:

   \[ N = \frac{2L}{i} + 1 \]

   Trong đó:

   • L là khoảng cách từ tâm đến biên của vùng giao thoa.
   • i là khoảng vân.

3. Vị trí vân sáng: Vị trí của vân sáng bậc \(k\) được xác định bằng công thức:

   \[ x_k = k \cdot i = k \cdot \frac{\lambda D}{a} \]

   Với \(k\) là bậc của vân sáng, có thể là số nguyên dương, âm hoặc bằng 0.

Ví dụ: Trong thí nghiệm I-âng về giao thoa ánh sáng, nếu ta biết khoảng cách giữa hai khe là 2 mm, khoảng cách từ hai khe đến màn quan sát là 1 m và ánh sáng sử dụng có bước sóng 600 nm, thì:

• Khoảng vân i được tính là: \[ i = \frac{600 \times 10^{-9} \times 1}{2 \times 10^{-3}} = 0.3 \, \text{mm} \]
• Giả sử khoảng cách từ tâm đến biên của vùng giao thoa là 15 mm, số vân sáng được tính là: \[ N = \frac{2 \times 15}{0.3} + 1 = 101 \, \text{vân} \]

Qua các bước tính toán trên, ta có thể xác định được số lượng và vị trí của các vân sáng trong hiện tượng giao thoa ánh sáng một cách chi tiết và chính xác.

Trong thí nghiệm giao thoa ánh sáng, vị trí vân sáng trung tâm có vai trò quan trọng trong việc xác định các vị trí vân sáng và vân tối trên màn. Vị trí của vân sáng trung tâm được xác định bằng công thức sau:

Công thức xác định vị trí vân sáng trung tâm:

Tọa độ của vân sáng trung tâm \(x_s\) được xác định bởi:

Trong đó:

• \(x_s\): Tọa độ của vân sáng trung tâm.
• \(\lambda\): Bước sóng ánh sáng.
• \(D\): Khoảng cách từ khe đến màn.
• \(a\): Khoảng cách giữa hai khe.
• \(k\): Thứ tự của vân sáng (với \(k = 0\), ta có vị trí vân sáng trung tâm).

Ví dụ cụ thể:

1. Trong thí nghiệm giao thoa ánh sáng Iâng, với khoảng cách từ khe đến màn là 2 m, khoảng cách giữa hai khe là 0,5 mm, và ánh sáng sử dụng có bước sóng là 0,6 µm, vị trí vân sáng trung tâm sẽ nằm tại:

Điều này có nghĩa là vân sáng trung tâm nằm tại vị trí giữa màn hình (tọa độ \(x = 0\)).

Việc xác định vị trí của các vân sáng tiếp theo cũng dựa vào công thức này, chỉ cần thay đổi giá trị \(k\) tương ứng.

Trong hiện tượng giao thoa ánh sáng, các vân tối được hình thành do sự triệt tiêu của các sóng ánh sáng từ hai nguồn sáng kết hợp. Để tính số vân tối trong một khoảng giới hạn nhất định, ta cần xác định các yếu tố cơ bản như khoảng cách giữa hai khe, bước sóng của ánh sáng, và khoảng cách từ các khe đến màn quan sát.

Giả sử ta có:

• Khoảng cách giữa hai khe: \(d\)
• Bước sóng của ánh sáng: \(\lambda\)
• Khoảng cách từ khe đến màn: \(D\)

Vị trí các vân tối được xác định bởi công thức:

Trong đó:

• \(y_k\) là vị trí của vân tối thứ \(k\) tính từ vân sáng trung tâm.
• \(k\) là số thứ tự của vân tối, với \(k = 0, 1, 2, \dots\)

Để tính số vân tối trong khoảng giới hạn từ \(y_1\) đến \(y_2\), ta làm như sau:

1. Tính giá trị của \(k_1\) tương ứng với \(y_1\) bằng cách giải phương trình: \[ y_1 = \left(k_1 + \dfrac{1}{2}\right)\dfrac{\lambda D}{d} \] Từ đó, suy ra: \[ k_1 = \dfrac{y_1 d}{\lambda D} - \dfrac{1}{2} \]
2. Tính giá trị của \(k_2\) tương ứng với \(y_2\) bằng cách giải phương trình: \[ y_2 = \left(k_2 + \dfrac{1}{2}\right)\dfrac{\lambda D}{d} \] Suy ra: \[ k_2 = \dfrac{y_2 d}{\lambda D} - \dfrac{1}{2} \]
3. Số vân tối trong khoảng từ \(y_1\) đến \(y_2\) được tính bằng: \[ N = k_2 - k_1 \] Với \(N\) là số vân tối cần tìm.

Với các bước trên, bạn có thể tính được số vân tối trong khoảng giới hạn bất kỳ. Hãy đảm bảo tính toán cẩn thận các giá trị để đạt được kết quả chính xác nhất.

Khoảng vân trong hiện tượng giao thoa ánh sáng là khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp. Để tính toán khoảng vân, ta có thể sử dụng công thức:

\[
i = \frac{\lambda D}{a}
\]

Trong đó:

• \(\lambda\): Bước sóng của ánh sáng (thường được đo bằng mét).
• \(D\): Khoảng cách từ hai khe đến màn (thường được đo bằng mét).
• \(a\): Khoảng cách giữa hai khe (thường được đo bằng mét).
• \(i\): Khoảng vân trên màn (thường được đo bằng mét).

Bước 1: Xác định các giá trị cần thiết từ đề bài. Thông thường, đề bài sẽ cung cấp giá trị của \( \lambda \), \( D \) và \( a \).

Bước 2: Thay các giá trị đã biết vào công thức để tính khoảng vân \( i \).

Ví dụ: Nếu đề bài cho \( \lambda = 600 \, \text{nm} \) (6 x 10^-7 m), \( D = 2 \, \text{m} \) và \( a = 0.1 \, \text{mm} \) (1 x 10^-4 m), ta có thể tính khoảng vân như sau:

\[
i = \frac{6 \times 10^{-7} \times 2}{1 \times 10^{-4}} = 0.012 \, \text{m} = 1.2 \, \text{cm}
\]

Bước 3: Kết luận, khoảng vân trên màn là 1.2 cm.

Lưu ý: Nếu đơn vị của các giá trị không đồng nhất, hãy chuyển đổi chúng về cùng một đơn vị trước khi tính toán để tránh sai sót.

Trong thí nghiệm giao thoa ánh sáng với khe Young, vân sáng là những vị trí mà ánh sáng từ hai nguồn kết hợp gặp nhau tại đó tạo thành sự tăng cường. Để xác định bậc của vân sáng, ta cần áp dụng công thức liên quan đến khoảng cách giữa các khe, bước sóng của ánh sáng và khoảng cách từ khe đến màn.

Công thức tính vị trí vân sáng:

Vị trí của vân sáng bậc \( k \) được xác định bằng công thức:

Trong đó:

• \( y_k \): Vị trí của vân sáng bậc \( k \).
• \( k \): Bậc của vân sáng (vân trung tâm có \( k = 0 \), các vân tiếp theo có \( k = 1, 2, 3, \dots \)).
• \( \lambda \): Bước sóng của ánh sáng.
• \( D \): Khoảng cách từ khe đến màn.
• \( a \): Khoảng cách giữa hai khe sáng.

Các bước thực hiện:

1. Xác định bước sóng \( \lambda \) của ánh sáng đang sử dụng.
2. Đo khoảng cách \( D \) từ khe đến màn và khoảng cách \( a \) giữa hai khe.
3. Tính toán vị trí \( y_k \) của vân sáng cho các bậc khác nhau \( k \) bằng công thức trên.
4. So sánh kết quả thu được với thực nghiệm để xác định chính xác bậc của từng vân sáng.

Ví dụ, nếu bước sóng của ánh sáng là \( \lambda = 600 \, nm \), khoảng cách từ khe đến màn là \( D = 2 \, m \) và khoảng cách giữa hai khe là \( a = 0.5 \, mm \), vị trí của vân sáng bậc 1 sẽ là:

Như vậy, vân sáng bậc 1 sẽ xuất hiện tại vị trí cách vân trung tâm 2.4 mm.

Áp dụng tương tự cho các bậc khác để xác định toàn bộ hệ thống vân sáng trên màn.

Để tính khoảng cách từ vân sáng đến màn trong hiện tượng giao thoa ánh sáng, chúng ta cần áp dụng công thức cơ bản của giao thoa khe Y-âng. Công thức này cho phép chúng ta xác định khoảng cách giữa các vân sáng hoặc vân tối và từ đó suy ra khoảng cách từ vân sáng đến màn.

1. Xác định các thông số:

   • a - Khoảng cách giữa hai khe sáng (khoảng cách giữa hai nguồn sáng đồng bộ).
   • D - Khoảng cách từ khe sáng đến màn.
   • λ - Bước sóng của ánh sáng.
   • x - Khoảng cách từ vân sáng bậc m đến màn (vị trí cần tính).

2. Công thức tính khoảng cách từ vân sáng đến màn:

   Công thức tổng quát để tính khoảng cách từ vân sáng bậc m đến màn là:

   \[
   x_m = \frac{m \cdot \lambda \cdot D}{a}
   \]

   Trong đó:

   • m là bậc của vân sáng (m = 0, ±1, ±2,...).
   • x_m là khoảng cách từ vân sáng bậc m đến vân sáng trung tâm.

3. Áp dụng công thức:

   Sau khi xác định được các thông số, ta áp dụng công thức trên để tính khoảng cách từ vân sáng cần tìm đến màn.

   Ví dụ: Nếu ta cần tìm khoảng cách từ vân sáng bậc 2 đến màn, ta sẽ có:

   \[
   x_2 = \frac{2 \cdot \lambda \cdot D}{a}
   \]

4. Kiểm tra kết quả:

   Sau khi tính toán, hãy kiểm tra lại kết quả để đảm bảo rằng các giá trị đã được thay thế đúng và kết quả cuối cùng là hợp lý.

Với phương pháp này, chúng ta có thể dễ dàng tính toán được khoảng cách từ bất kỳ vân sáng nào đến màn trong thí nghiệm giao thoa ánh sáng.

Trong các bài tập về giao thoa ánh sáng, việc xác định số vân tối giữa hai vân sáng liền kề là một dạng bài tập thường gặp và đòi hỏi sự chính xác trong tính toán. Để giải quyết dạng bài tập này, ta cần thực hiện các bước sau:

1. Bước 1: Xác định khoảng cách giữa hai vân sáng liền kề.

   Khoảng cách này được gọi là khoảng vân và được ký hiệu là \(i\). Công thức tính khoảng vân là:

   \[i = \dfrac{\lambda D}{a}\]

   Trong đó:

   • \(\lambda\) là bước sóng ánh sáng
   • \(D\) là khoảng cách từ nguồn sáng đến màn
   • \(a\) là khoảng cách giữa hai khe hẹp trong thí nghiệm

2. Bước 2: Tính số vân tối giữa hai vân sáng.

   Số vân tối giữa hai vân sáng liền kề chính là số nguyên các lần vị trí của vân tối nằm giữa. Công thức tính số vân tối là:

   \[N = \dfrac{i - i_{min}}{i_{max} - i_{min}} - 1\]

   Trong đó:

   • \(N\) là số vân tối giữa hai vân sáng
   • \(i_{min}\) là vị trí của vân tối đầu tiên
   • \(i_{max}\) là vị trí của vân tối cuối cùng

3. Bước 3: Kiểm tra và đối chiếu kết quả.

   So sánh kết quả vừa tính toán với thực tế hoặc dữ liệu bài cho để xác nhận tính chính xác của câu trả lời.

Việc hiểu rõ và nắm chắc các bước trên sẽ giúp bạn tự tin giải quyết các bài tập liên quan đến xác định số vân tối giữa hai vân sáng, từ đó củng cố kiến thức về hiện tượng giao thoa ánh sáng.

Trong hiện tượng giao thoa sóng, sự chênh lệch pha giữa hai sóng đóng vai trò quan trọng trong việc xác định các điểm cực đại và cực tiểu giao thoa. Để tính toán sự chênh lệch pha giữa hai sóng, ta có thể làm theo các bước sau:

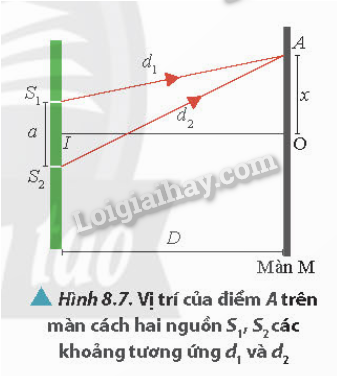
1. Xác định các đại lượng cần thiết: Đầu tiên, chúng ta cần biết khoảng cách từ hai nguồn sóng đến điểm đang xét (d₁ và d₂), bước sóng \(\lambda\), và các điều kiện ban đầu về pha của hai nguồn sóng.

2. Hiệu đường đi: Tính hiệu đường đi của hai sóng tới điểm xét, được biểu diễn bằng công thức:

   \[\Delta d = d_2 - d_1\]

3. Tính sự chênh lệch pha: Sử dụng hiệu đường đi để tính sự chênh lệch pha giữa hai sóng tại điểm M, công thức được biểu diễn như sau:

   \[\Delta \varphi = \dfrac{2\pi \Delta d}{\lambda}\]

   Trong đó, \(\Delta \varphi\) là sự chênh lệch pha, \(\Delta d\) là hiệu đường đi, và \(\lambda\) là bước sóng của sóng.

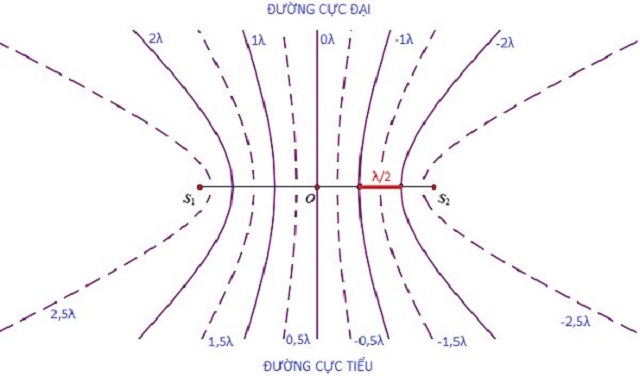
4. Xác định vị trí vân giao thoa: Dựa trên sự chênh lệch pha, chúng ta có thể xác định vị trí của các vân sáng và vân tối trên màn giao thoa:

   • Vân sáng (cực đại giao thoa) xảy ra khi \(\Delta \varphi = 2k\pi\), với \(k\) là số nguyên.

   • Vân tối (cực tiểu giao thoa) xảy ra khi \(\Delta \varphi = (2k+1)\pi\).

5. Áp dụng vào bài tập cụ thể: Khi làm bài tập, ta chỉ cần thay các giá trị cụ thể vào các công thức trên để tính toán sự chênh lệch pha và xác định các vị trí giao thoa.

Phương pháp này giúp ta hiểu rõ hơn về cơ chế của hiện tượng giao thoa sóng và cách tính toán sự chênh lệch pha giữa hai sóng tại một điểm bất kỳ.