Bề Rộng Trường Giao Thoa: Hiểu Rõ Hiện Tượng Vật Lý Quan Trọng

Trong vật lý, trường giao thoa là một hiện tượng xảy ra khi hai hoặc nhiều sóng gặp nhau và tạo ra các vùng có cường độ sóng tăng hoặc giảm. Bề rộng trường giao thoa là khoảng cách giữa hai vị trí tương ứng trên hai vân sáng hoặc hai vân tối liên tiếp trong hiện tượng giao thoa ánh sáng.

Công Thức Tính Bề Rộng Trường Giao Thoa

Trong thí nghiệm Y-âng về giao thoa ánh sáng, khoảng vân \(i\) là khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp, được tính theo công thức:

Trong đó:

• \(\lambda\): Bước sóng ánh sáng.
• \(D\): Khoảng cách từ hai khe đến màn quan sát.
• \(a\): Khoảng cách giữa hai khe.

Ứng Dụng Của Bề Rộng Trường Giao Thoa

Bề rộng trường giao thoa là một khái niệm quan trọng trong các nghiên cứu và ứng dụng liên quan đến sóng ánh sáng. Nó giúp xác định các đặc điểm của nguồn sáng, ví dụ như bước sóng và cường độ. Điều này có ý nghĩa trong nhiều lĩnh vực từ vật lý lượng tử đến kỹ thuật quang học.

Bài Tập Mẫu

Dưới đây là một ví dụ về cách tính bề rộng trường giao thoa trong thí nghiệm Y-âng:

Giả sử khoảng cách giữa hai khe là \(a = 1 \, \text{mm}\), khoảng cách từ hai khe tới màn là \(D = 2 \, \text{m}\), và ánh sáng đơn sắc có bước sóng \( \lambda = 0.6 \, \mu\text{m}\). Khoảng vân sẽ được tính như sau:

Như vậy, bề rộng trường giao thoa trong trường hợp này là 1.2 mm.

Kết Luận

Bề rộng trường giao thoa là một yếu tố quan trọng giúp hiểu rõ hơn về bản chất của ánh sáng và sóng. Nó không chỉ cung cấp thông tin về tính chất của ánh sáng mà còn giúp phát triển các công nghệ dựa trên hiện tượng giao thoa, như kỹ thuật đo lường chính xác trong quang học.

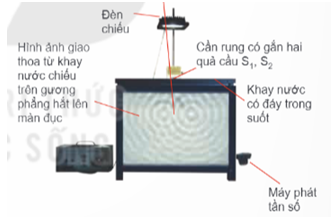
Hiện tượng giao thoa ánh sáng là một trong những minh chứng rõ ràng cho tính chất sóng của ánh sáng. Khi hai hay nhiều chùm sáng gặp nhau, chúng có thể giao thoa, tạo ra các vùng có cường độ ánh sáng khác nhau, bao gồm các vân sáng và vân tối.

Quá trình giao thoa này xảy ra khi các sóng ánh sáng từ hai nguồn đồng bộ gặp nhau, dẫn đến sự tăng cường hoặc triệt tiêu lẫn nhau tại các điểm khác nhau trong không gian. Vị trí của các vân sáng và vân tối được xác định bằng hiệu đường đi của các sóng.

• Khi hiệu đường đi giữa hai sóng là bội số nguyên của bước sóng \(\lambda\), tức là \(\Delta d = m\lambda\) với \(m\) là số nguyên, ta sẽ quan sát được các vân sáng (tăng cường giao thoa).
• Khi hiệu đường đi là bội số lẻ của nửa bước sóng \(\lambda\), tức là \(\Delta d = (m + 0.5)\lambda\), ta sẽ quan sát được các vân tối (triệt tiêu giao thoa).

Hiện tượng giao thoa ánh sáng không chỉ cung cấp bằng chứng mạnh mẽ về bản chất sóng của ánh sáng, mà còn được ứng dụng rộng rãi trong các lĩnh vực như quang học, nhiếp ảnh, và nghiên cứu khoa học. Ví dụ điển hình là thí nghiệm Y-âng (Young) về giao thoa ánh sáng, nơi hai khe hẹp được chiếu sáng bởi cùng một nguồn ánh sáng, tạo ra mô hình các vân giao thoa trên màn quan sát.

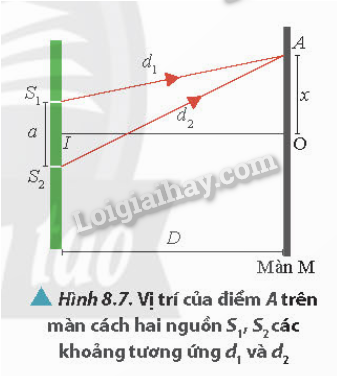
Để tính toán khoảng vân, tức là khoảng cách giữa hai vân sáng (hoặc hai vân tối) liên tiếp, ta sử dụng công thức:

Trong đó:

• \(\lambda\): Bước sóng của ánh sáng.
• \(D\): Khoảng cách từ khe đến màn.
• \(a\): Khoảng cách giữa hai khe.

Với công thức trên, ta có thể xác định khoảng cách giữa các vân giao thoa và từ đó hiểu rõ hơn về các yếu tố ảnh hưởng đến hiện tượng giao thoa ánh sáng. Hiện tượng này không chỉ mang ý nghĩa lý thuyết mà còn có giá trị thực tiễn cao trong công nghệ đo lường và quang học.

Bề rộng trường giao thoa là một khái niệm quan trọng trong việc nghiên cứu hiện tượng giao thoa ánh sáng. Nó liên quan đến khoảng cách giữa các điểm mà sóng ánh sáng giao thoa với nhau, tạo ra các vân sáng và vân tối trên màn hình. Bề rộng này được xác định bởi nhiều yếu tố như bước sóng của ánh sáng, khoảng cách giữa các khe giao thoa và khoảng cách từ khe đến màn quan sát.

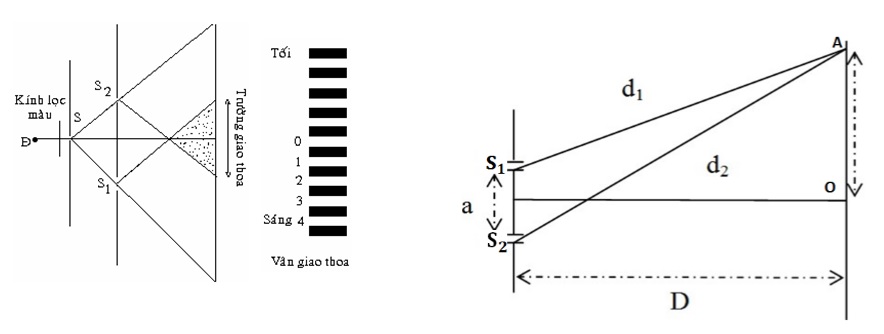
Để hiểu rõ hơn về bề rộng trường giao thoa, chúng ta có thể xem xét thí nghiệm Y-âng, nơi hai khe hẹp được chiếu sáng đồng thời bởi một nguồn ánh sáng đơn sắc. Khi ánh sáng đi qua hai khe này, chúng tạo ra hai chùm sóng giao thoa với nhau và tạo ra một hệ thống các vân sáng, vân tối trên màn hình.

Khoảng cách giữa các vân sáng hoặc vân tối liên tiếp được gọi là khoảng vân \((i)\), và nó được xác định bởi công thức:

Trong đó:

• \(\lambda\): Bước sóng của ánh sáng.
• \(D\): Khoảng cách từ các khe đến màn.
• \(a\): Khoảng cách giữa hai khe.

Bề rộng trường giao thoa có thể được tính toán bằng cách xác định số lượng các vân sáng hoặc vân tối nằm trong một khoảng xác định trên màn. Ví dụ, nếu chúng ta xét một vùng có chiều dài \(L\) trên màn hình, bề rộng trường giao thoa \((W)\) có thể được tính bằng công thức:

Trong đó \(L\) là chiều dài của vùng giao thoa mà chúng ta đang xét. Giá trị của \(W\) sẽ cho biết số lượng vân giao thoa xuất hiện trong vùng đó.

Khi khoảng cách giữa các khe hoặc bước sóng của ánh sáng thay đổi, bề rộng trường giao thoa cũng sẽ thay đổi. Điều này có nghĩa là bằng cách điều chỉnh các tham số này, chúng ta có thể kiểm soát và dự đoán được mô hình giao thoa, ứng dụng trong các lĩnh vực như quang học và đo lường.

Dưới đây là một số bài tập nhằm giúp bạn củng cố kiến thức về bề rộng trường giao thoa. Các bài tập được thiết kế để bạn có thể áp dụng công thức và lý thuyết vào việc giải quyết các vấn đề cụ thể.

1. Bài tập 1:

   Một thí nghiệm giao thoa với ánh sáng có bước sóng \(\lambda = 600 \, \text{nm}\), khoảng cách giữa hai khe \(a = 0,5 \, \text{mm}\), và khoảng cách từ khe đến màn \(D = 2 \, \text{m}\). Hãy tính khoảng vân \(i\) và bề rộng trường giao thoa \(W\) trong vùng dài \(L = 10 \, \text{cm}\).

   Lời giải:

   Khoảng vân được tính theo công thức:

   \[ i = \frac{\lambda D}{a} = \frac{600 \times 10^{-9} \times 2}{0,5 \times 10^{-3}} = 2,4 \, \text{mm} \]

   Bề rộng trường giao thoa trong vùng dài \(L\) là:

   \[ W = \frac{L}{i} = \frac{0,1}{0,0024} \approx 41,67 \, \text{vân} \]

2. Bài tập 2:

   Trong một thí nghiệm giao thoa, khoảng cách giữa hai khe là \(1 \, \text{mm}\), bước sóng ánh sáng sử dụng là \(500 \, \text{nm}\), và khoảng cách từ khe đến màn là \(1,5 \, \text{m}\). Tính bề rộng trường giao thoa cho một vùng dài \(L = 8 \, \text{cm}\).

   Lời giải:

   Khoảng vân:

   \[ i = \frac{\lambda D}{a} = \frac{500 \times 10^{-9} \times 1,5}{1 \times 10^{-3}} = 0,75 \, \text{mm} \]

   Bề rộng trường giao thoa:

   \[ W = \frac{L}{i} = \frac{0,08}{0,00075} \approx 106,67 \, \text{vân} \]

3. Bài tập 3:

   Một thí nghiệm với ánh sáng đơn sắc có bước sóng \(650 \, \text{nm}\). Khoảng cách từ khe đến màn là \(2,5 \, \text{m}\) và khoảng cách giữa hai khe là \(0,4 \, \text{mm}\). Tính bề rộng trường giao thoa trên màn dài \(L = 12 \, \text{cm}\).

   Lời giải:

   Khoảng vân:

   \[ i = \frac{\lambda D}{a} = \frac{650 \times 10^{-9} \times 2,5}{0,4 \times 10^{-3}} = 4,06 \, \text{mm} \]

   Bề rộng trường giao thoa:

   \[ W = \frac{L}{i} = \frac{0,12}{0,00406} \approx 29,56 \, \text{vân} \]