Lý thuyết giao thoa sóng 12: Hướng dẫn toàn diện và bài tập vận dụng

Trong chương trình Vật lý lớp 12, giao thoa sóng là một trong những khái niệm quan trọng, liên quan đến sự tương tác giữa hai hay nhiều sóng cùng loại. Dưới đây là tổng hợp chi tiết về lý thuyết giao thoa sóng bao gồm các khái niệm cơ bản, công thức, và các ví dụ minh họa.

1. Khái niệm giao thoa sóng

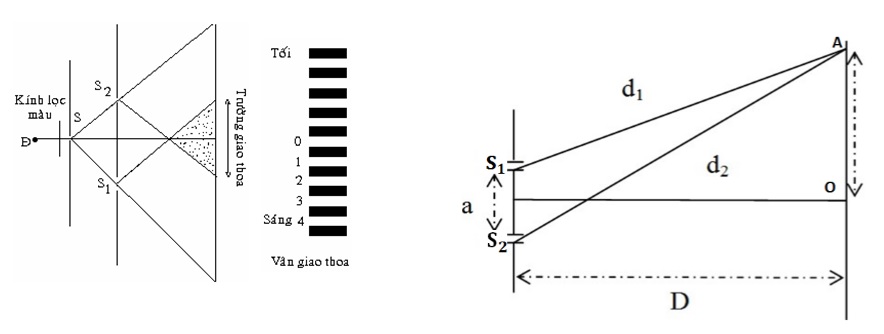
• Giao thoa sóng là hiện tượng xảy ra khi hai hay nhiều sóng kết hợp gặp nhau và tạo ra các vùng có biên độ dao động lớn (cực đại giao thoa) hoặc nhỏ (cực tiểu giao thoa).
• Các đường giao thoa cực đại thường có hình dạng đường hypebol.

2. Điều kiện để xảy ra giao thoa sóng

• Hai nguồn sóng phải là nguồn kết hợp, tức là chúng phải có cùng tần số, cùng pha hoặc có hiệu số pha không đổi theo thời gian.
• Sóng phải có biên độ không đổi trong quá trình truyền.

3. Công thức giao thoa sóng

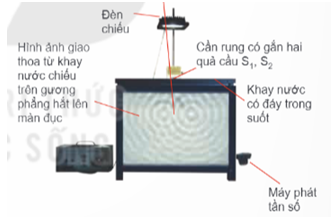
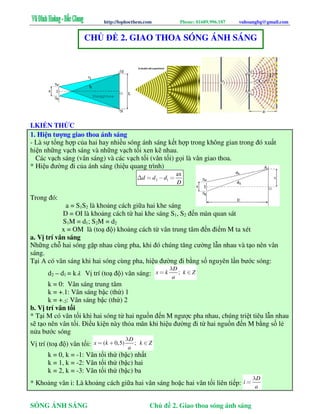
• Phương trình sóng từ hai nguồn sóng S₁ và S₂ đến điểm M:


\[
u_{1M} = A \cos\left(2\pi\left(\frac{t}{T} - \frac{d_1}{\lambda}\right)\right)
\]
\[
u_{2M} = A \cos\left(2\pi\left(\frac{t}{T} - \frac{d_2}{\lambda}\right)\right)
\]

• Phương trình sóng tổng hợp tại điểm M:


\[
u_M = u_{1M} + u_{2M} = 2A \cos\left(\frac{\pi(d_1 - d_2)}{\lambda}\right) \cos\left(2\pi\left(\frac{t}{T} - \frac{d_1 + d_2}{2\lambda}\right)\right)
\]

4. Vị trí các cực đại và cực tiểu giao thoa

• Cực đại giao thoa: xảy ra tại những vị trí mà hiệu đường đi từ hai nguồn sóng bằng một số nguyên lần bước sóng:


\[
d_2 - d_1 = k\lambda, \quad k \in \mathbb{Z}
\]

• Cực tiểu giao thoa: xảy ra tại những vị trí mà hiệu đường đi từ hai nguồn sóng bằng một số nửa nguyên lần bước sóng:


\[
d_2 - d_1 = \left(k + \frac{1}{2}\right)\lambda, \quad k \in \mathbb{Z}
\]

5. Ứng dụng trong giải bài tập

Khi giải các bài tập liên quan đến giao thoa sóng, học sinh cần xác định rõ điều kiện giao thoa và áp dụng đúng công thức tính vị trí các cực đại và cực tiểu. Các bài tập thường yêu cầu tính toán bước sóng, khoảng cách giữa các vân giao thoa, hoặc vị trí cụ thể của một điểm dao động mạnh nhất hoặc yếu nhất.

6. Bài tập mẫu

1. Bài tập 1: Tìm khoảng cách giữa hai vân cực đại liên tiếp trên mặt nước khi biết bước sóng là 5 cm và khoảng cách giữa hai nguồn sóng là 50 cm.
2. Bài tập 2: Xác định số lượng vân cực đại trên đoạn thẳng nối hai nguồn sóng khi biết khoảng cách giữa hai nguồn sóng là 100 cm và bước sóng là 10 cm.

Trong bài viết này, chúng ta sẽ khám phá chi tiết về lý thuyết giao thoa sóng lớp 12. Các phần sẽ được trình bày một cách rõ ràng, từ các khái niệm cơ bản đến ứng dụng và bài tập. Hãy cùng bắt đầu với mục lục tổng hợp dưới đây:

• 1. Khái niệm Giao thoa Sóng

  Giới thiệu về hiện tượng giao thoa sóng, bao gồm định nghĩa và ví dụ minh họa về sự gặp nhau của hai sóng kết hợp và các vân giao thoa.

• 2. Điều kiện để xảy ra Giao thoa Sóng

  Các yếu tố cần thiết để giao thoa sóng xảy ra, bao gồm điều kiện về tần số, pha và biên độ của các nguồn sóng kết hợp.

• 3. Phương trình Sóng trong Giao thoa

  Trình bày các phương trình mô tả sự kết hợp của hai sóng tại một điểm trong vùng giao thoa, bao gồm cả phương trình tổng quát và ví dụ cụ thể:

  
  \[
  u_M = 2A \cos\left(\frac{\pi(d_1 - d_2)}{\lambda}\right) \cos\left(2\pi\left(\frac{t}{T} - \frac{d_1 + d_2}{2\lambda}\right)\right)
  \]

• 4. Vị trí các Cực đại và Cực tiểu Giao thoa

  Hướng dẫn cách xác định các vị trí trên mặt phẳng nơi giao thoa sóng tạo ra các cực đại và cực tiểu, bao gồm công thức và giải thích cụ thể:

  
  \[
  d_2 - d_1 = k\lambda, \quad d_2 - d_1 = \left(k + \frac{1}{2}\right)\lambda, \quad k \in \mathbb{Z}
  \]

• 5. Ứng dụng của Giao thoa Sóng

  Khám phá các ứng dụng thực tiễn của hiện tượng giao thoa sóng trong đời sống và công nghệ, như trong truyền thông, đo lường sóng và các hiện tượng âm học.

• 6. Bài tập và Ví dụ thực hành

  Các bài tập thực hành giúp củng cố kiến thức về giao thoa sóng, bao gồm các bài tập tính toán vị trí các vân, xác định bước sóng và tần số sóng.

• 7. Các yếu tố ảnh hưởng đến Giao thoa Sóng

  Phân tích các yếu tố như môi trường truyền sóng, khoảng cách giữa các nguồn sóng và tần số ảnh hưởng đến hiện tượng giao thoa sóng.

• 8. Kết luận và Ý nghĩa của Giao thoa Sóng

  Tóm tắt lại các kiến thức chính về giao thoa sóng và nhấn mạnh tầm quan trọng của hiện tượng này trong vật lý và các lĩnh vực liên quan.

Dưới đây là một số dạng bài tập phổ biến về giao thoa sóng trong chương trình Vật lý lớp 12, kèm theo hướng dẫn giải chi tiết. Những bài tập này giúp học sinh nắm vững kiến thức và phát triển kỹ năng giải quyết vấn đề liên quan đến hiện tượng giao thoa sóng.

• Bài tập 1: Tính vị trí các cực đại và cực tiểu

  Hai nguồn sóng \( S_1 \) và \( S_2 \) dao động cùng pha, phát ra sóng với bước sóng \(\lambda = 5 \, \text{cm}\). Tìm khoảng cách từ điểm \( M \) nằm trên đường trung trực của \( S_1S_2 \) đến các vị trí có cực đại và cực tiểu giao thoa.

  Giải:

  1. Xác định hiệu đường đi: \(\Delta d = |d_2 - d_1|\).
  2. Điều kiện cực đại: \(\Delta d = k\lambda\).
  3. Điều kiện cực tiểu: \(\Delta d = \left(k + \frac{1}{2}\right)\lambda\).
  4. Tính toán các vị trí thỏa mãn điều kiện trên.
• Bài tập 2: Xác định bước sóng từ hiện tượng giao thoa

  Hai nguồn sóng cách nhau 60 cm dao động cùng pha. Trên đoạn thẳng nối hai nguồn, có 4 vân cực đại. Tính bước sóng của sóng.

  Giải:

  1. Xác định khoảng cách giữa hai nguồn \( d = 60 \, \text{cm} \).
  2. Đếm số vân cực đại trên đoạn thẳng nối hai nguồn.
  3. Sử dụng công thức \( d_2 - d_1 = k\lambda \) để tính bước sóng \(\lambda\).
• Bài tập 3: Phương trình sóng tổng hợp tại một điểm

  Tại điểm \( M \) cách hai nguồn \( S_1 \) và \( S_2 \) lần lượt là 40 cm và 45 cm, viết phương trình sóng tổng hợp biết biên độ sóng là \( A = 2 \, \text{cm} \) và tần số sóng là \( f = 10 \, \text{Hz} \).

  Giải:

  1. Viết phương trình sóng từ từng nguồn đến điểm \( M \):

  
  \[
  u_{1M} = 2 \cos\left(2\pi\left(\frac{t}{T} - \frac{40}{\lambda}\right)\right)
  \]
  \[
  u_{2M} = 2 \cos\left(2\pi\left(\frac{t}{T} - \frac{45}{\lambda}\right)\right)
  \]

  2. Tính phương trình sóng tổng hợp tại \( M \):

  
  \[
  u_M = u_{1M} + u_{2M}
  \]

• Bài tập 4: Xác định khoảng cách giữa các vân giao thoa

  Hai nguồn sóng cách nhau 100 cm, phát ra sóng với bước sóng \( \lambda = 5 \, \text{cm} \). Tính khoảng cách giữa hai vân cực đại liên tiếp.

  Giải:

  1. Xác định khoảng cách giữa các vân cực đại theo công thức:

  
  \[
  \Delta x = \frac{\lambda D}{d}
  \]

  2. Thay các giá trị đã biết vào công thức để tìm kết quả.
• Bài tập 5: Giao thoa sóng cơ trên mặt nước

  Trên mặt nước, hai nguồn sóng cách nhau 50 cm phát sóng với tần số 5 Hz. Tính khoảng cách giữa các vân giao thoa trên mặt nước.

  Giải:

  1. Xác định bước sóng của sóng trên mặt nước từ tần số và vận tốc sóng.
  2. Tính khoảng cách giữa các vân giao thoa dựa trên bước sóng và khoảng cách giữa hai nguồn.