Chủ đề chuyển động thẳng biến đổi đều bài 9: Chuyển động thẳng biến đổi đều bài 9 cung cấp nền tảng vững chắc cho việc hiểu rõ về các khái niệm vật lý quan trọng, từ phương trình vận tốc đến đồ thị và các bài toán thực tế. Bài viết này sẽ giúp bạn nắm vững kiến thức và vận dụng linh hoạt các công thức, đồng thời cải thiện kỹ năng giải quyết bài tập liên quan.
Mục lục
- Chuyển động thẳng biến đổi đều - Bài 9 Vật Lý 10
- 2. Công thức cơ bản trong chuyển động thẳng biến đổi đều
- 3. Đồ thị vận tốc - thời gian
- 4. Các bài toán liên quan đến chuyển động thẳng biến đổi đều
- 5. Ứng dụng của chuyển động thẳng biến đổi đều
- 6. Bài tập và giải chi tiết về chuyển động thẳng biến đổi đều
- 7. Các lưu ý và sai lầm thường gặp
Chuyển động thẳng biến đổi đều - Bài 9 Vật Lý 10
Chuyển động thẳng biến đổi đều là một phần quan trọng trong chương trình Vật Lý lớp 10, đặc biệt ở bài 9. Dưới đây là tổng hợp thông tin chi tiết và đầy đủ về bài học này, bao gồm khái niệm, phương trình chuyển động và cách tính các đại lượng liên quan.
1. Khái niệm chuyển động thẳng biến đổi đều
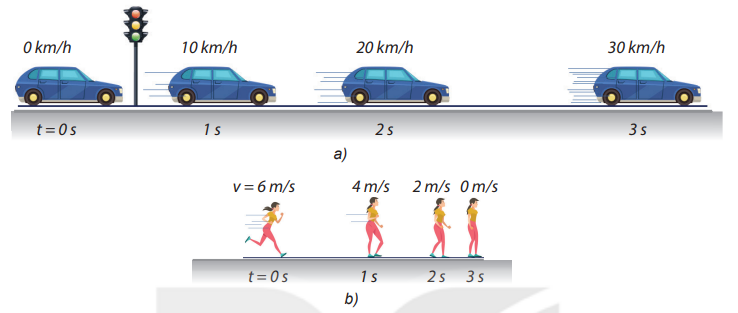
Chuyển động thẳng biến đổi đều là chuyển động trong đó vận tốc của vật thay đổi đều theo thời gian. Nó có hai loại:
- Chuyển động thẳng nhanh dần đều: Vận tốc của vật tăng dần theo thời gian.
- Chuyển động thẳng chậm dần đều: Vận tốc của vật giảm dần theo thời gian.
2. Phương trình chuyển động thẳng biến đổi đều
Phương trình chuyển động thẳng biến đổi đều có thể biểu diễn dưới các dạng sau:
- Phương trình vận tốc:
\[
v = v_0 + a t
\]
trong đó:
- \(v\) là vận tốc tại thời điểm \(t\)
- \(v_0\) là vận tốc ban đầu
- \(a\) là gia tốc
- Phương trình quãng đường: \[ s = v_0 t + \frac{1}{2} a t^2 \]
- Phương trình liên hệ giữa vận tốc và quãng đường: \[ v^2 = v_0^2 + 2 a s \]
3. Đồ thị trong chuyển động thẳng biến đổi đều
Có hai loại đồ thị thường gặp trong chuyển động thẳng biến đổi đều:
- Đồ thị vận tốc - thời gian (v - t): Đồ thị là một đường thẳng nghiêng với góc phụ thuộc vào gia tốc.
- Đồ thị quãng đường - thời gian (s - t): Đồ thị là một đường parabol vì quãng đường tỷ lệ bậc hai với thời gian.
4. Cách tính gia tốc trong chuyển động thẳng biến đổi đều
Gia tốc \(a\) trong chuyển động thẳng biến đổi đều có thể được tính bằng công thức:
Gia tốc là đại lượng đo lường mức độ thay đổi vận tốc theo thời gian. Nếu \(a > 0\), chuyển động là nhanh dần; nếu \(a < 0\), chuyển động là chậm dần.
5. Ví dụ minh họa
Dưới đây là một ví dụ về cách tính quãng đường và vận tốc trong chuyển động thẳng biến đổi đều:
- Giả sử một ô tô bắt đầu chuyển động với vận tốc ban đầu \(v_0 = 5\, \text{m/s}\), gia tốc \(a = 2\, \text{m/s}^2\). Sau 3 giây, vận tốc của ô tô là bao nhiêu?
- Áp dụng công thức: \[ v = v_0 + a t = 5 + 2 \times 3 = 11\, \text{m/s} \]
6. Các bài tập liên quan
Để hiểu rõ hơn về chuyển động thẳng biến đổi đều, học sinh có thể thực hành các bài tập sau:
- Bài tập về tính quãng đường khi biết vận tốc ban đầu và gia tốc.
- Bài tập vẽ đồ thị vận tốc - thời gian và quãng đường - thời gian.
- Bài tập tính vận tốc tại một thời điểm bất kỳ trong chuyển động.
Kết luận
Chuyển động thẳng biến đổi đều là một khái niệm quan trọng trong Vật lý lớp 10, giúp học sinh hiểu rõ hơn về cách các vật thể di chuyển trong không gian. Các công thức và đồ thị liên quan sẽ hỗ trợ cho việc giải quyết các bài toán chuyển động thực tế.
.png)
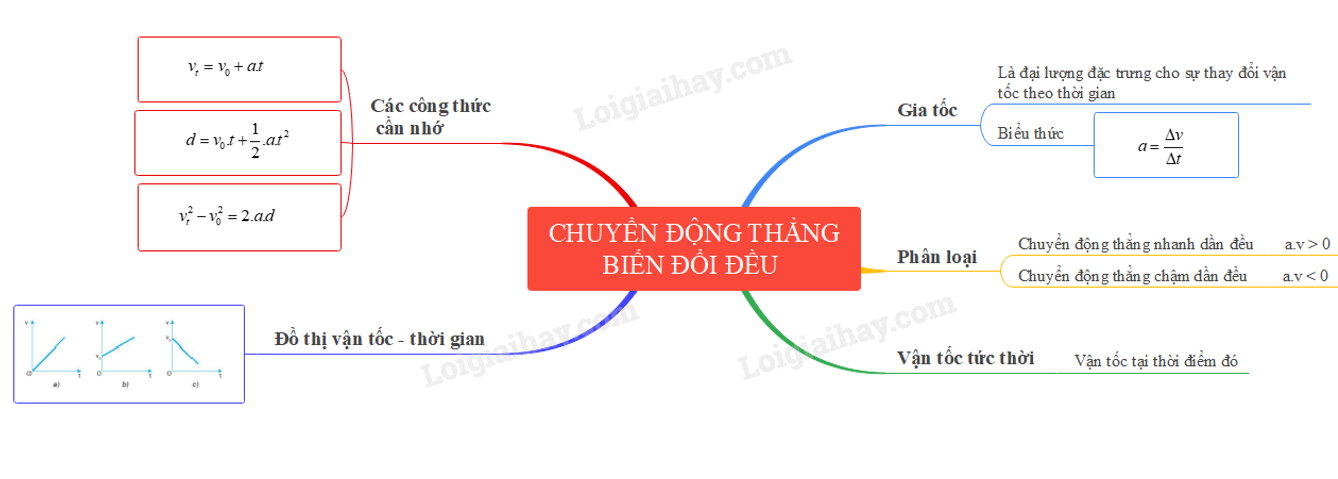
2. Công thức cơ bản trong chuyển động thẳng biến đổi đều
Chuyển động thẳng biến đổi đều là chuyển động mà vận tốc của vật thay đổi đều theo thời gian, nghĩa là gia tốc của vật không đổi. Trong quá trình này, các công thức cơ bản bao gồm vận tốc, quãng đường và gia tốc. Dưới đây là các công thức liên quan:
- Gia tốc: Gia tốc trong chuyển động thẳng biến đổi đều được tính theo công thức: \[ a = \frac{\Delta v}{\Delta t} = \frac{v_t - v_0}{t - t_0} \] với \( a \) là gia tốc (hằng số), \( v_t \) và \( v_0 \) lần lượt là vận tốc tại thời điểm \( t \) và \( t_0 \), \( t - t_0 \) là khoảng thời gian.
- Vận tốc: Vận tốc tức thời của vật trong chuyển động thẳng biến đổi đều được xác định bởi: \[ v = v_0 + a \cdot t \] Trong đó, \( v_0 \) là vận tốc ban đầu và \( a \) là gia tốc.
- Quãng đường: Công thức tính quãng đường mà vật đi được trong khoảng thời gian \( t \) là: \[ s = v_0 \cdot t + \frac{1}{2} a \cdot t^2 \] Đây là công thức phổ biến trong bài toán chuyển động thẳng biến đổi đều.
- Đồ thị vận tốc-thời gian: Đồ thị vận tốc theo thời gian trong chuyển động này là một đường thẳng, độ dốc của đường thẳng chính là gia tốc \( a \).
3. Đồ thị vận tốc - thời gian
Trong chuyển động thẳng biến đổi đều, đồ thị vận tốc - thời gian (v - t) là một đường thẳng. Vận tốc tức thời của vật thay đổi tuyến tính theo thời gian, biểu thị qua phương trình:
Trong đó:
- \(v_0\): Vận tốc ban đầu
- \(a\): Gia tốc của vật
- \(t\): Thời gian chuyển động
Đồ thị vận tốc - thời gian có thể biểu diễn dưới dạng một đường thẳng dốc lên nếu gia tốc dương (chuyển động nhanh dần đều) hoặc dốc xuống nếu gia tốc âm (chuyển động chậm dần đều). Diện tích bên dưới đồ thị này tương ứng với quãng đường mà vật đã đi được trong khoảng thời gian đó.
Ví dụ: Nếu vận tốc của vật thay đổi đều từ \(v_0\) đến \(v\) trong thời gian \(t\), quãng đường \(s\) đi được có thể tính bằng diện tích hình thang được tạo ra bởi đồ thị:
Đồ thị này là công cụ hữu ích để phân tích và mô tả quá trình chuyển động của vật theo thời gian.

4. Các bài toán liên quan đến chuyển động thẳng biến đổi đều
Các bài toán liên quan đến chuyển động thẳng biến đổi đều thường tập trung vào các khía cạnh như quãng đường, vận tốc, và thời gian trong quá trình chuyển động. Phương pháp giải bài toán bao gồm:
- Viết phương trình chuyển động cho mỗi vật, sử dụng công thức: \[ x = x_0 + v_0 t + \frac{1}{2} a t^2 \]
- Tìm thời điểm và vị trí gặp nhau giữa hai vật khi xét chuyển động đối chiều hoặc cùng chiều.
- Sử dụng các công thức gia tốc và vận tốc để tính toán bài toán về quãng đường, ví dụ: \[ s = v_0 t + \frac{1}{2} a t^2 \]
Ví dụ, nếu hai vật di chuyển ngược chiều với nhau trên quãng đường xác định, bạn có thể viết phương trình chuyển động cho từng vật và tìm thời điểm hai vật gặp nhau bằng cách giải hệ phương trình.

5. Ứng dụng của chuyển động thẳng biến đổi đều
Chuyển động thẳng biến đổi đều có rất nhiều ứng dụng trong đời sống và các lĩnh vực khoa học kỹ thuật. Một số ví dụ nổi bật bao gồm:
- Trong giao thông, việc tính toán khoảng cách dừng xe dựa vào gia tốc âm khi phanh gấp là ứng dụng thực tế của chuyển động thẳng chậm dần đều.
- Trong ngành hàng không, chuyển động của máy bay khi cất cánh hoặc hạ cánh có thể được xem như chuyển động thẳng nhanh dần đều hoặc chậm dần đều.
- Các hệ thống tự động hóa, robot cũng sử dụng các phương trình chuyển động để lập trình quá trình di chuyển, nhằm đảm bảo hiệu quả và chính xác.
Việc áp dụng chuyển động thẳng biến đổi đều giúp con người cải tiến các quá trình di chuyển, tiết kiệm năng lượng và tăng cường độ an toàn trong nhiều ngành công nghiệp.

6. Bài tập và giải chi tiết về chuyển động thẳng biến đổi đều
Dưới đây là một số bài tập phổ biến liên quan đến chuyển động thẳng biến đổi đều, kèm theo giải chi tiết từng bước để giúp bạn hiểu rõ hơn về phương pháp giải các dạng bài toán này.
Bài tập 1: Tính vận tốc của một vật
Đề bài: Một vật chuyển động thẳng biến đổi đều từ trạng thái nghỉ, gia tốc của vật là \(a = 2 \, \text{m/s}^2\). Sau 5 giây, vận tốc của vật là bao nhiêu?
Lời giải:
- Áp dụng công thức tính vận tốc: \[ v = v_0 + at \]
- Vì vật bắt đầu từ trạng thái nghỉ nên \(v_0 = 0\), do đó: \[ v = 0 + 2 \times 5 = 10 \, \text{m/s} \]
- Vậy vận tốc của vật sau 5 giây là \(10 \, \text{m/s}\).
Bài tập 2: Tính quãng đường đi được
Đề bài: Một vật chuyển động thẳng nhanh dần đều với vận tốc ban đầu là \(v_0 = 2 \, \text{m/s}\) và gia tốc \(a = 3 \, \text{m/s}^2\). Tính quãng đường đi được sau 4 giây.
Lời giải:
- Áp dụng công thức tính quãng đường: \[ s = v_0 t + \frac{1}{2}at^2 \]
- Thay số vào công thức: \[ s = 2 \times 4 + \frac{1}{2} \times 3 \times 4^2 \]
- Kết quả: \[ s = 8 + 24 = 32 \, \text{m} \]
- Vậy quãng đường vật đi được sau 4 giây là 32 mét.
Bài tập 3: Tính thời gian dừng lại của vật
Đề bài: Một xe đang chuyển động với vận tốc \(v = 20 \, \text{m/s}\) thì bắt đầu hãm phanh với gia tốc \(a = -5 \, \text{m/s}^2\). Hỏi sau bao lâu xe dừng lại?
Lời giải:
- Áp dụng công thức: \[ v = v_0 + at \]
- Khi xe dừng lại, \(v = 0\), do đó: \[ 0 = 20 + (-5)t \]
- Giải ra: \[ t = \frac{20}{5} = 4 \, \text{giây} \]
- Vậy thời gian xe dừng lại là 4 giây.
Các bài tập trên giúp bạn hiểu rõ hơn cách áp dụng các công thức của chuyển động thẳng biến đổi đều vào thực tế. Hãy luyện tập nhiều dạng bài tập để nắm vững kiến thức và cách giải.
XEM THÊM:
7. Các lưu ý và sai lầm thường gặp
Khi nghiên cứu và giải bài tập liên quan đến chuyển động thẳng biến đổi đều, học sinh thường gặp một số sai lầm phổ biến. Dưới đây là các lưu ý và sai lầm thường gặp, giúp học sinh tránh mắc phải và đạt hiệu quả tốt hơn trong quá trình học tập:
7.1 Lưu ý trong tính toán
- Chú ý đơn vị: Trong các bài tập về chuyển động thẳng biến đổi đều, cần đặc biệt chú ý đến đơn vị của các đại lượng vật lý như vận tốc, gia tốc, quãng đường và thời gian. Đảm bảo tất cả các đại lượng được quy đổi về cùng hệ đơn vị trước khi thực hiện tính toán.
- Sử dụng đúng công thức: Các công thức vận tốc tức thời \( v = v_0 + at \), quãng đường \( s = v_0 t + \frac{1}{2} a t^2 \) và gia tốc \( a = \frac{v - v_0}{t} \) cần được áp dụng đúng ngữ cảnh và điều kiện.
- Kiểm tra lại các bước tính: Sau khi giải bài toán, hãy dành thời gian kiểm tra lại toàn bộ các bước tính toán để đảm bảo rằng không có sai sót nào xảy ra trong quá trình giải.
7.2 Sai lầm thường gặp khi vẽ đồ thị
- Nhầm lẫn giữa đồ thị vận tốc - thời gian và quãng đường - thời gian: Một trong những sai lầm thường gặp là học sinh hay nhầm lẫn giữa các loại đồ thị này. Đồ thị vận tốc - thời gian là dạng tuyến tính, trong khi đồ thị quãng đường - thời gian có thể là đường cong (parabol).
- Sai sót khi xác định độ dốc của đồ thị: Độ dốc của đồ thị vận tốc - thời gian chính là gia tốc, nhưng nhiều học sinh thường nhầm lẫn giữa độ dốc và các giá trị khác trong đồ thị. Cần lưu ý rằng độ dốc càng lớn thì gia tốc càng lớn.
- Xác định sai khoảng thời gian: Khi giải các bài tập yêu cầu vẽ đồ thị, cần đặc biệt chú ý xác định chính xác khoảng thời gian được cho trong bài toán, tránh tính sai hoặc bỏ qua một phần nào đó của thời gian.