Chủ đề chuyên đề chuyển động thẳng đều: Chuyên đề chuyển động thẳng đều cung cấp những kiến thức cơ bản và nâng cao về chuyển động thẳng đều. Bài viết sẽ giúp bạn nắm vững phương pháp lập phương trình, giải bài tập cũng như hiểu sâu hơn về ứng dụng thực tiễn của nó. Hãy cùng khám phá chuyên đề quan trọng này trong vật lý lớp 10 qua các ví dụ chi tiết và bài tập thực hành.
Mục lục
Chuyên đề Chuyển Động Thẳng Đều
Chuyển động thẳng đều là một trong những kiến thức cơ bản của môn Vật lý, đặc biệt trong chương trình lớp 10. Đây là dạng chuyển động trong đó vật di chuyển theo đường thẳng với vận tốc không đổi. Dưới đây là nội dung chi tiết về chuyên đề này.
1. Định nghĩa chuyển động thẳng đều
Chuyển động thẳng đều là chuyển động trong đó vật đi theo đường thẳng với vận tốc không thay đổi theo thời gian. Phương trình cơ bản của chuyển động thẳng đều có dạng:
\[
x = x_0 + v \cdot t
\]
Trong đó:
- \( x \): Vị trí của vật tại thời điểm t.
- \( x_0 \): Vị trí ban đầu của vật.
- \( v \): Vận tốc không đổi của vật.
- \( t \): Thời gian.
2. Quãng đường đi được trong chuyển động thẳng đều
Quãng đường vật đi được sau một khoảng thời gian \( \Delta t \) được tính theo công thức:
\[
s = |v| \cdot \Delta t
\]
Trong đó \( v \) là vận tốc của vật, và \( \Delta t \) là thời gian chuyển động.
3. Đồ thị của chuyển động thẳng đều
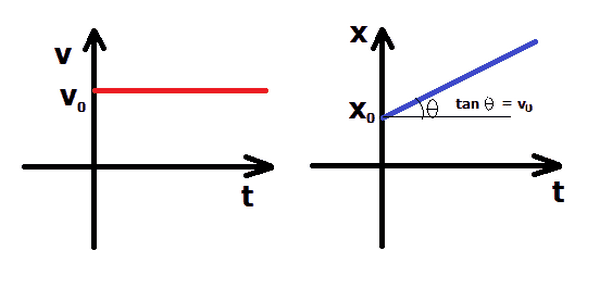
- Đồ thị tọa độ theo thời gian: Đồ thị này biểu diễn mối quan hệ giữa tọa độ và thời gian, có dạng một đường thẳng. Phương trình đồ thị tọa độ là: \[ x = x_0 + v \cdot t \] Đồ thị là một đường thẳng với độ dốc là vận tốc \( v \).
- Đồ thị vận tốc theo thời gian: Đồ thị này là một đường thẳng song song với trục thời gian, cho thấy vận tốc không đổi suốt quá trình chuyển động. Công thức: \[ v = v_0 \]
4. Bài tập ví dụ
Dưới đây là một số bài tập ứng dụng về chuyển động thẳng đều:
- Một vật di chuyển với vận tốc 5 m/s. Tính quãng đường đi được trong 2 giờ.
- Cho phương trình \( x = 5t + 2 \). Tìm vị trí của vật sau 3 giây.
- Một xe đi từ A đến B cách nhau 100 km với vận tốc 40 km/h. Tính thời gian đi hết quãng đường.
5. Kết luận
Chuyển động thẳng đều là kiến thức nền tảng trong vật lý và có ứng dụng quan trọng trong nhiều lĩnh vực như cơ học, giao thông và các hiện tượng tự nhiên. Việc nắm vững chuyên đề này giúp học sinh có cái nhìn sâu sắc hơn về các quy luật chuyển động trong đời sống thực tế.
| Công thức | Ý nghĩa |
|---|---|
| \( x = x_0 + v \cdot t \) | Phương trình tính vị trí theo thời gian trong chuyển động thẳng đều. |
| \( s = v \cdot t \) | Quãng đường đi được trong chuyển động thẳng đều. |

.png)
I. Khái niệm về chuyển động thẳng đều
Chuyển động thẳng đều là chuyển động trong đó một vật di chuyển trên một đường thẳng với vận tốc không đổi. Điều này có nghĩa là khoảng cách mà vật di chuyển trong các khoảng thời gian bằng nhau là như nhau.
- Chuyển động theo một quỹ đạo thẳng.
- Vận tốc có độ lớn và hướng không thay đổi.
- Phương trình chuyển động: \[ x = x_0 + v \cdot t \], trong đó:
- \(x_0\) là tọa độ ban đầu của vật.
- \(v\) là vận tốc của vật.
- \(t\) là thời gian vật di chuyển.
Ví dụ, một chiếc ô tô chuyển động thẳng đều khi nó đi với vận tốc không đổi trên một đoạn đường thẳng, không thay đổi hướng và không tăng tốc.
II. Phương trình chuyển động thẳng đều
Phương trình chuyển động thẳng đều là công thức giúp chúng ta xác định vị trí của vật theo thời gian khi nó di chuyển với vận tốc không đổi trên một đường thẳng.
Công thức tổng quát của phương trình chuyển động thẳng đều là:
- \[ x = x_0 + v \cdot t \]
- \(x\): vị trí của vật tại thời điểm \(t\).
- \(x_0\): vị trí ban đầu của vật (tại thời điểm \(t = 0\)).
- \(v\): vận tốc không đổi của vật.
- \(t\): thời gian vật di chuyển.
Trong đó:
- Vận tốc \(v\) có thể dương (nếu vật chuyển động theo chiều dương của trục tọa độ) hoặc âm (nếu vật chuyển động theo chiều ngược lại).
- Phương trình này giúp ta biết vị trí của vật sau một khoảng thời gian bất kỳ \(t\).
Ví dụ: Một chiếc xe bắt đầu di chuyển từ điểm \(A\) với vận tốc \(v = 10 \, km/h\), sau \(2 \, h\) xe sẽ cách vị trí ban đầu bao nhiêu km?
- Giải: Sử dụng phương trình \[ x = x_0 + v \cdot t \], với \( x_0 = 0 \), \( v = 10 \, km/h \), \( t = 2 \, h \), ta có: \[ x = 0 + 10 \cdot 2 = 20 \, km \].

III. Đồ thị của chuyển động thẳng đều
Đồ thị của chuyển động thẳng đều có vai trò quan trọng trong việc biểu diễn mối quan hệ giữa vị trí và thời gian của vật chuyển động. Từ đồ thị, ta có thể trực quan hóa và phân tích đặc điểm của chuyển động.
1. Đồ thị tọa độ - thời gian
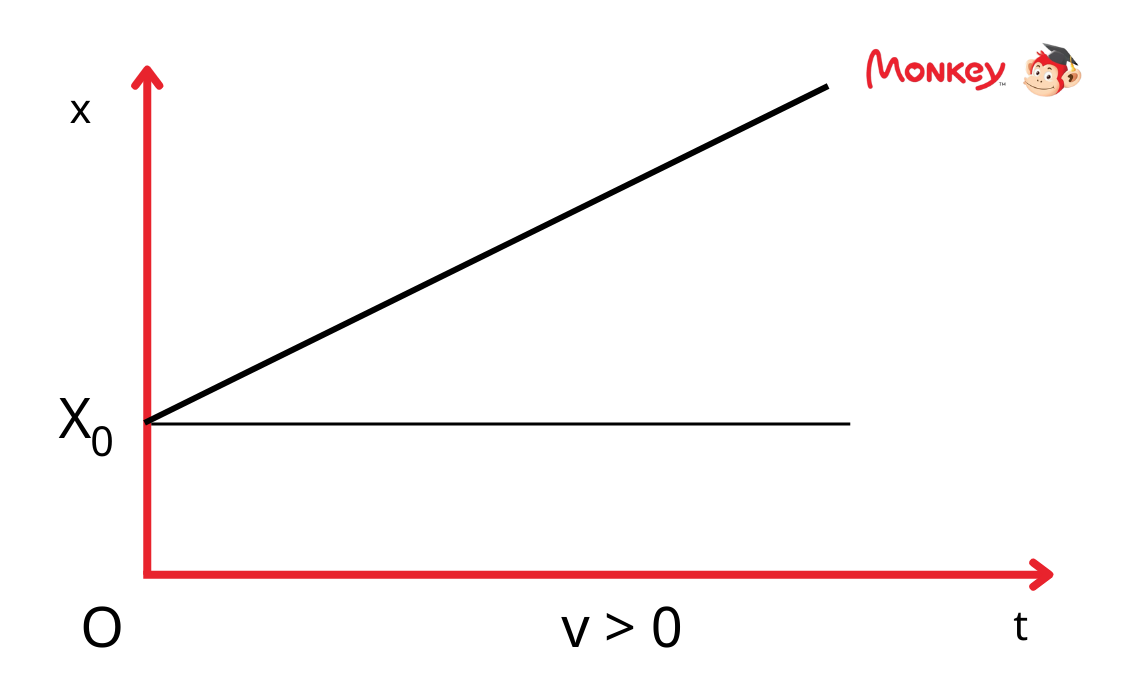
Đồ thị biểu diễn mối quan hệ giữa vị trí \(x\) và thời gian \(t\) trong chuyển động thẳng đều là một đường thẳng. Phương trình đồ thị có dạng:
- \[ x = x_0 + v \cdot t \]
- Trong đó:
- \(x\): tọa độ của vật tại thời điểm \(t\).
- \(x_0\): tọa độ ban đầu của vật.
- \(v\): vận tốc không đổi của vật.
Độ dốc của đồ thị chính là vận tốc \(v\) của vật. Nếu \(v > 0\), đồ thị sẽ dốc lên; nếu \(v < 0\), đồ thị sẽ dốc xuống.
2. Đồ thị vận tốc - thời gian
Đồ thị biểu diễn mối quan hệ giữa vận tốc \(v\) và thời gian \(t\) trong chuyển động thẳng đều là một đường thẳng song song với trục thời gian. Điều này cho thấy vận tốc của vật không thay đổi theo thời gian, hay \(v = hằng số\).
| Thời gian \(t\) | 0 | 1 | 2 | 3 |
| Vận tốc \(v\) | 5 | 5 | 5 | 5 |
Ví dụ, một vật chuyển động với vận tốc không đổi \(v = 5 \, m/s\), đồ thị vận tốc - thời gian sẽ là một đường thẳng nằm ngang tại \(v = 5\).

IV. Bài tập và phương pháp giải
Dưới đây là một số bài tập về chuyển động thẳng đều, kèm theo phương pháp giải chi tiết giúp học sinh nắm vững kiến thức và kỹ năng giải bài tập.
1. Bài tập cơ bản
- Bài 1: Một xe ô tô đang chuyển động thẳng đều với vận tốc \(v = 60 \, km/h\). Sau bao lâu xe đi được quãng đường \(S = 120 \, km\)?
- Phương pháp giải: Sử dụng công thức \[ S = v \cdot t \], suy ra thời gian \(t = \frac{S}{v} = \frac{120}{60} = 2 \, giờ\).
2. Bài tập nâng cao
- Bài 2: Một người đi bộ từ điểm \(A\) đến điểm \(B\) với vận tốc \(v_1 = 4 \, km/h\), sau đó quay lại từ \(B\) đến \(A\) với vận tốc \(v_2 = 6 \, km/h\). Tính vận tốc trung bình của người đó trong suốt hành trình.
- Phương pháp giải: Vận tốc trung bình được tính bằng công thức: \[ v_{tb} = \frac{2 \cdot v_1 \cdot v_2}{v_1 + v_2} = \frac{2 \cdot 4 \cdot 6}{4 + 6} = 4.8 \, km/h. \]
3. Bài tập thách thức
- Bài 3: Một đoàn tàu dài \(200 \, m\) chuyển động thẳng đều với vận tốc \(v = 72 \, km/h\) vượt qua một cây cầu dài \(300 \, m\). Tính thời gian đoàn tàu vượt qua toàn bộ cây cầu.
- Phương pháp giải: Để tính thời gian, trước tiên ta tính tổng quãng đường mà đoàn tàu cần di chuyển là \(S = 200 + 300 = 500 \, m\). Vận tốc của đoàn tàu là \(v = 72 \, km/h = 20 \, m/s\). Sử dụng công thức: \[ t = \frac{S}{v} = \frac{500}{20} = 25 \, giây. \]

V. Ứng dụng của chuyển động thẳng đều trong thực tiễn
Chuyển động thẳng đều là một dạng chuyển động cơ bản và có nhiều ứng dụng thực tiễn trong đời sống. Những ứng dụng này giúp chúng ta hiểu rõ hơn về các nguyên tắc vật lý và cách chúng ảnh hưởng đến các hệ thống, thiết bị và quá trình xung quanh.
1. Giao thông và vận tải
- Trong giao thông đường bộ, vận tốc trung bình của xe cộ di chuyển theo đường thẳng đều được sử dụng để tính toán thời gian di chuyển và tiết kiệm nhiên liệu.
- Hệ thống tàu điện, tàu hoả đều dựa trên nguyên lý chuyển động thẳng đều trong các quãng đường ổn định để duy trì vận tốc an toàn và tiết kiệm năng lượng.
2. Dây chuyền sản xuất công nghiệp
- Trong các nhà máy sản xuất, các băng chuyền thường hoạt động với tốc độ đều đặn, tuân theo chuyển động thẳng đều, để đảm bảo quy trình lắp ráp chính xác và ổn định.
- Việc duy trì tốc độ chuyển động đều giúp tăng năng suất và giảm thiểu rủi ro trong quy trình sản xuất.
3. Chuyển động của vệ tinh và tàu vũ trụ
- Trong vũ trụ, các vệ tinh thường di chuyển theo quỹ đạo với vận tốc không đổi, ứng dụng nguyên lý chuyển động thẳng đều khi không bị ảnh hưởng bởi lực cản.
- Điều này giúp duy trì liên lạc, định vị, và theo dõi chính xác các vệ tinh từ Trái Đất.
4. Trong thể thao
- Các môn thể thao như chạy marathon, đua xe đạp đều ứng dụng chuyển động thẳng đều để duy trì tốc độ và tiết kiệm năng lượng trong suốt quá trình thi đấu.
- Vận động viên thường tính toán và duy trì tốc độ di chuyển ổn định để đạt được thành tích tốt nhất.
XEM THÊM:
VI. Đề kiểm tra và bài tập mẫu
Để nắm vững kiến thức về chuyển động thẳng đều, việc luyện tập qua các đề kiểm tra và bài tập mẫu là rất cần thiết. Dưới đây là một số bài tập tiêu biểu và hướng dẫn giải chi tiết giúp học sinh củng cố kiến thức và chuẩn bị tốt cho các kỳ thi.
1. Đề kiểm tra lý thuyết
- Câu 1: Định nghĩa chuyển động thẳng đều? Nêu các đặc điểm của chuyển động này.
- Câu 2: Viết phương trình chuyển động thẳng đều và giải thích các đại lượng trong phương trình.
- Câu 3: Vẽ đồ thị vận tốc - thời gian và tọa độ - thời gian của một chuyển động thẳng đều.
2. Bài tập tự luận
Một xe ô tô chuyển động thẳng đều với vận tốc \( v = 60 \, \text{km/h} \). Tính quãng đường xe đi được sau 2 giờ.
Vật chuyển động thẳng đều có phương trình \( x = 5t + 3 \, (\text{m}) \), với \( t \) tính bằng giây. Hãy xác định vận tốc của vật và vị trí ban đầu.
Một người chạy với vận tốc không đổi là \( v = 10 \, \text{m/s} \). Sau bao lâu người đó đi được 200 m?
3. Bài tập trắc nghiệm
| Câu hỏi | Đáp án |
| Chuyển động thẳng đều là gì? | A. Chuyển động có vận tốc không đổi theo thời gian |
| Phương trình của chuyển động thẳng đều có dạng nào? | B. \( x = v_0 t + x_0 \) |