Chủ đề lý thuyết chuyển động thẳng đều: Lý thuyết chuyển động thẳng đều là nền tảng quan trọng trong Vật lý. Bài viết này sẽ cung cấp cho bạn kiến thức chi tiết về các phương trình, đồ thị và ứng dụng thực tế của chuyển động thẳng đều. Qua đó, bạn sẽ hiểu rõ hơn về cách áp dụng lý thuyết này vào các hiện tượng hàng ngày và bài tập vận dụng.
Mục lục
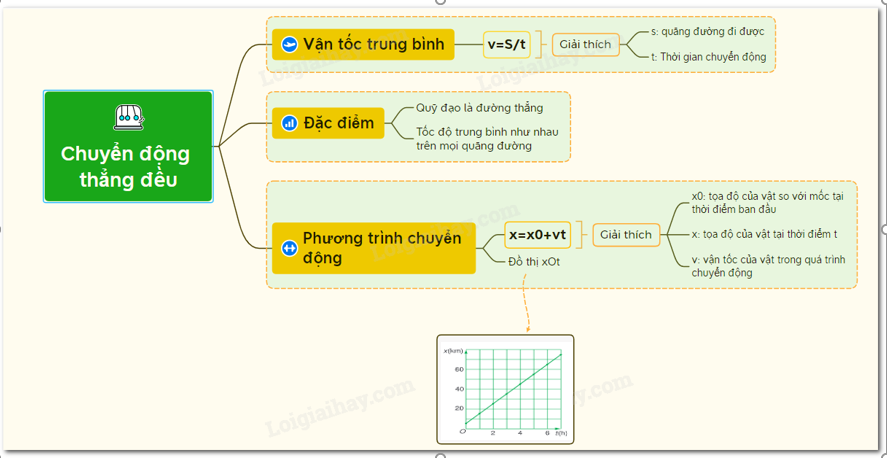
Lý thuyết chuyển động thẳng đều
Chuyển động thẳng đều là một trong những khái niệm cơ bản trong vật lý, thường được giảng dạy trong chương trình học lớp 10. Chuyển động này có quỹ đạo là đường thẳng và vận tốc của vật không thay đổi theo thời gian. Dưới đây là các khái niệm, phương trình và công thức liên quan đến chuyển động thẳng đều.
1. Định nghĩa chuyển động thẳng đều
Chuyển động thẳng đều là chuyển động có quỹ đạo là đường thẳng và vận tốc không đổi, tức là độ lớn của vận tốc (tốc độ) giữ nguyên theo thời gian.
2. Đặc điểm của chuyển động thẳng đều
- Quỹ đạo của vật là một đường thẳng.
- Vận tốc không đổi: Tốc độ của vật không thay đổi theo thời gian.
- Gia tốc bằng 0 vì vận tốc không thay đổi.
3. Công thức tính quãng đường và vận tốc trong chuyển động thẳng đều
Công thức tính quãng đường đi được trong chuyển động thẳng đều là:
\[
s = v \cdot t
\]
Trong đó:
- \(s\) là quãng đường đi được (đơn vị: mét, km,...)
- \(v\) là vận tốc của vật (đơn vị: m/s, km/h,...)
- \(t\) là thời gian chuyển động (đơn vị: giây, giờ,...)
4. Phương trình chuyển động thẳng đều
Phương trình tọa độ của chuyển động thẳng đều có dạng:
\[
x = x_0 + v \cdot t
\]
Trong đó:
- \(x\) là tọa độ của vật tại thời điểm \(t\).
- \(x_0\) là tọa độ ban đầu của vật tại thời điểm \(t_0\).
- \(v\) là vận tốc của vật.
- \(t\) là thời gian kể từ lúc bắt đầu chuyển động.
5. Đồ thị tọa độ - thời gian của chuyển động thẳng đều
Đồ thị tọa độ - thời gian của chuyển động thẳng đều là một đường thẳng nghiêng với độ dốc bằng vận tốc của vật. Nếu vật chuyển động theo chiều dương, đường thẳng sẽ đi lên, ngược lại nếu chuyển động theo chiều âm, đường thẳng sẽ đi xuống.
6. Bài tập minh họa
Một chiếc xe chuyển động thẳng đều với vận tốc \(v = 20\,\text{km/h}\). Sau thời gian \(t = 2\,\text{h}\), quãng đường xe đi được là:
\[
s = v \cdot t = 20 \cdot 2 = 40\,\text{km}
\]
Như vậy, xe đã đi được 40 km sau 2 giờ chuyển động.
7. Ứng dụng của chuyển động thẳng đều
Chuyển động thẳng đều có nhiều ứng dụng trong thực tế như trong việc tính toán lộ trình di chuyển của phương tiện giao thông, thiết kế hệ thống giao thông công cộng và trong nhiều lĩnh vực kỹ thuật khác.
.png)
2. Phương trình chuyển động thẳng đều
Phương trình chuyển động thẳng đều biểu diễn mối quan hệ giữa vị trí của vật theo thời gian khi vật di chuyển với vận tốc không đổi trên một đường thẳng. Công thức của phương trình này được viết như sau:
Trong đó:
- \(x\) là tọa độ của vật tại thời điểm \(t\)
- \(x_0\) là tọa độ ban đầu của vật
- \(v\) là vận tốc không đổi của vật
- \(t\) là thời gian vật chuyển động
Phương trình này cho phép chúng ta tính được vị trí của vật tại một thời điểm cụ thể nếu biết vận tốc, thời gian, và tọa độ ban đầu. Quá trình này giúp dễ dàng phân tích sự chuyển động của vật trong các bài toán Vật lý.
Một số bước tính toán trong phương trình:
- Xác định tọa độ ban đầu \(x_0\).
- Xác định vận tốc \(v\) của vật (đơn vị: m/s).
- Nhập thời gian \(t\) mà vật đã di chuyển.
- Áp dụng phương trình để tính tọa độ \(x\) của vật tại thời điểm \(t\).
3. Đồ thị tọa độ - thời gian của chuyển động thẳng đều
Đồ thị tọa độ - thời gian của chuyển động thẳng đều là một đường thẳng trên mặt phẳng tọa độ, biểu thị mối quan hệ giữa vị trí của vật và thời gian. Dưới đây là các bước phân tích đồ thị này:
- Xác định hệ trục tọa độ: Trục hoành (OX) biểu diễn thời gian \(t\) và trục tung (OY) biểu diễn tọa độ \(x\).
- Phương trình cơ bản: Phương trình của chuyển động thẳng đều là \(x = x_0 + v \cdot t\), với \(x_0\) là tọa độ ban đầu, \(v\) là vận tốc.
- Đặc điểm của đồ thị:
- Đường thẳng nghiêng: Nếu \(v > 0\), đường thẳng dốc lên, vật di chuyển theo chiều dương.
- Đường thẳng nghiêng xuống: Nếu \(v < 0\), đường thẳng dốc xuống, vật di chuyển theo chiều âm.
- Đường thẳng ngang: Nếu \(v = 0\), vật đứng yên và đồ thị là một đường ngang.
- Ví dụ minh họa: Xét vật có \(v = 2\) m/s và tọa độ ban đầu \(x_0 = 0\), phương trình sẽ là \(x = 2t\). Đồ thị trong trường hợp này sẽ là đường thẳng dốc lên với độ dốc là 2.
Đồ thị tọa độ - thời gian giúp chúng ta dễ dàng quan sát sự thay đổi vị trí của vật theo thời gian và phân tích các đặc điểm của chuyển động.

4. Ứng dụng thực tế của chuyển động thẳng đều
Chuyển động thẳng đều có nhiều ứng dụng thực tế trong cuộc sống hàng ngày và các ngành công nghiệp. Dưới đây là một số ví dụ tiêu biểu về cách ứng dụng chuyển động này:
- Phương tiện giao thông: Trong các đoạn đường thẳng, xe ô tô hoặc tàu hỏa thường di chuyển với vận tốc không đổi, ứng dụng nguyên lý của chuyển động thẳng đều để tính thời gian và quãng đường.
- Đo lường vận tốc: Các thiết bị đo vận tốc như máy đo tốc độ radar sử dụng công thức của chuyển động thẳng đều để xác định tốc độ của phương tiện di chuyển trên đường.
- Hệ thống băng chuyền: Trong dây chuyền sản xuất, băng chuyền thường chuyển động thẳng đều với vận tốc ổn định để vận chuyển sản phẩm qua các khâu sản xuất và đóng gói.
- Chuyển động của vệ tinh: Vệ tinh di chuyển theo quỹ đạo có thể được mô hình hóa là chuyển động thẳng đều trong các điều kiện lý tưởng khi không có lực tác dụng làm thay đổi tốc độ.
Các ứng dụng này minh chứng rõ ràng cho sự quan trọng của lý thuyết chuyển động thẳng đều trong cả khoa học và đời sống.

5. Bài tập về chuyển động thẳng đều
Dưới đây là một số bài tập thực hành về chuyển động thẳng đều, giúp các em học sinh củng cố kiến thức và áp dụng lý thuyết vào thực tế:
- Bài tập 1: Một xe ô tô bắt đầu di chuyển từ vị trí \(x_0 = 0\) m với vận tốc không đổi \(v = 20 \, \text{m/s}\). Hãy tính vị trí của xe sau \(t = 5\) giây.
- Giải: Sử dụng phương trình \(x = x_0 + v \cdot t\), ta có:
- \[ x = 0 + 20 \cdot 5 = 100 \, \text{m} \]
- Bài tập 2: Một người đi bộ với vận tốc không đổi \(v = 1,5 \, \text{m/s}\) trong thời gian \(t = 10\) phút. Tính quãng đường mà người đó đi được.
- Giải: Đổi thời gian về giây: \(t = 10 \cdot 60 = 600 \, \text{s}\).
- Sử dụng phương trình \(x = v \cdot t\), ta có:
- \[ x = 1,5 \cdot 600 = 900 \, \text{m} \]
- Bài tập 3: Một tàu hỏa di chuyển với vận tốc không đổi và đi được quãng đường 120 km trong 2 giờ. Hãy tính vận tốc của tàu.
- Giải: Sử dụng công thức \(v = \frac{x}{t}\), ta có:
- \[ v = \frac{120 \, \text{km}}{2 \, \text{h}} = 60 \, \text{km/h} \]
Các bài tập này giúp các em nắm vững cách áp dụng công thức vào thực tế, từ đó hiểu rõ hơn về chuyển động thẳng đều.



















