Chọn phát biểu đúng về chuyển động thẳng đều: Kiến thức cơ bản và ứng dụng

Chuyển động thẳng đều là một loại chuyển động đơn giản trong vật lý. Trong chuyển động này, vật thể di chuyển theo một đường thẳng với vận tốc không đổi theo thời gian. Để hiểu rõ hơn, ta sẽ tìm hiểu về các khía cạnh như phương trình chuyển động, đặc điểm của chuyển động thẳng đều, và các bài tập ví dụ.

Phương Trình Chuyển Động Thẳng Đều

Phương trình của chuyển động thẳng đều có dạng:

\[ x = x_0 + v \cdot t \]

• \( x \): Tọa độ của vật tại thời điểm \( t \)
• \( x_0 \): Tọa độ ban đầu của vật
• \( v \): Vận tốc của vật (không đổi)
• \( t \): Thời gian chuyển động

Đặc Điểm Của Chuyển Động Thẳng Đều

Chuyển động thẳng đều có những đặc điểm nổi bật sau:

• Quỹ đạo là một đường thẳng
• Vận tốc không thay đổi
• Gia tốc bằng \(0\)
• Quãng đường đi được tỉ lệ thuận với thời gian di chuyển

Công Thức Liên Quan

Quãng đường \(s\) mà vật đi được trong chuyển động thẳng đều được tính bằng công thức:

\[ s = v \cdot t \]

Với:

• \( s \): Quãng đường di chuyển
• \( t \): Thời gian di chuyển

Đồ Thị Tọa Độ - Thời Gian

Đồ thị biểu diễn mối quan hệ giữa tọa độ và thời gian của một vật chuyển động thẳng đều là một đường thẳng:

• Trục hoành: Thời gian (\(t\))
• Trục tung: Tọa độ (\(x\))
• Độ dốc của đường thẳng chính là vận tốc (\(v\))

Bài Tập Ví Dụ

Ví dụ: Một ô tô di chuyển thẳng đều với vận tốc \( v = 60 \, km/h \). Tính quãng đường ô tô đi được sau 2 giờ?

Lời giải:

Quãng đường \( s \) được tính theo công thức: \( s = v \cdot t \)

Thay số vào ta có:

\[ s = 60 \, km/h \cdot 2 \, h = 120 \, km \]

Vậy, ô tô đi được quãng đường 120 km sau 2 giờ.

Kết Luận

Chuyển động thẳng đều là một dạng chuyển động cơ bản trong vật lý. Nó có ứng dụng trong nhiều lĩnh vực như giao thông, vận tải, và kỹ thuật. Việc hiểu rõ đặc điểm và phương trình chuyển động giúp chúng ta phân tích và giải các bài toán liên quan một cách dễ dàng.

1. Định nghĩa chuyển động thẳng đều

Chuyển động thẳng đều là chuyển động của một vật trên quỹ đạo thẳng với vận tốc không đổi. Điều này có nghĩa là trong suốt quá trình chuyển động, vật di chuyển đều đặn, quãng đường đi được trong mỗi đơn vị thời gian là như nhau.

• Vận tốc không thay đổi theo thời gian
• Quỹ đạo chuyển động là đường thẳng
• Gia tốc của vật bằng 0

2. Đặc điểm chính

Để hiểu rõ hơn về chuyển động thẳng đều, chúng ta cần nắm vững các đặc điểm chính sau:

1. Quỹ đạo của chuyển động là một đường thẳng.
2. Vận tốc của vật không thay đổi theo thời gian, được tính bằng công thức: \[ v = \frac{s}{t} \] trong đó \( v \) là vận tốc, \( s \) là quãng đường đi được, và \( t \) là thời gian.
3. Gia tốc của vật bằng 0, tức là: \[ a = \frac{\Delta v}{\Delta t} = 0 \] với \( a \) là gia tốc, \( \Delta v \) là sự thay đổi vận tốc, và \( \Delta t \) là sự thay đổi thời gian.

3. Phương trình chuyển động thẳng đều

Phương trình mô tả chuyển động thẳng đều có dạng:

• \( x \): tọa độ của vật tại thời điểm \( t \)
• \( x_0 \): tọa độ ban đầu của vật
• \( v \): vận tốc không đổi của vật
• \( t_0 \): thời gian ban đầu

4. Công thức tính quãng đường

Quãng đường vật đi được sau thời gian \( \Delta t \) được tính bằng:

Trong đó:

• \( s \): quãng đường đi được
• \( v \): vận tốc không đổi
• \( \Delta t \): khoảng thời gian vật chuyển động

Chuyển động thẳng đều là một dạng chuyển động đơn giản nhất trong cơ học, nơi vật di chuyển theo một đường thẳng với vận tốc không đổi. Dưới đây là các công thức cơ bản liên quan đến chuyển động thẳng đều:

• Phương trình chuyển động thẳng đều:

Phương trình mô tả vị trí của vật tại thời điểm \( t \) được cho bởi:

\[ x = x_0 + v \cdot t \]

Trong đó:

• \( x \) là vị trí của vật tại thời điểm \( t \)
• \( x_0 \) là vị trí ban đầu của vật
• \( v \) là vận tốc không đổi của vật
• \( t \) là thời gian chuyển động
• Công thức tính quãng đường:

Quãng đường đi được trong chuyển động thẳng đều được tính bằng:

\[ S = v \cdot t \]

Trong đó:

• \( S \) là quãng đường đi được
• \( v \) là vận tốc của vật
• \( t \) là thời gian chuyển động
• Công thức tính vận tốc trung bình:

Vận tốc trung bình của vật trong một khoảng thời gian được xác định bởi:

\[ v_{tb} = \frac{S}{t} \]

Trong đó:

• \( v_{tb} \) là vận tốc trung bình
• \( S \) là tổng quãng đường đi được
• \( t \) là tổng thời gian chuyển động

Ví dụ: Một ô tô chuyển động thẳng đều với vận tốc 60 km/h trong 2 giờ và sau đó giảm xuống còn 40 km/h trong 3 giờ. Vận tốc trung bình của ô tô trong toàn bộ thời gian là:

Những công thức trên giúp chúng ta hiểu rõ hơn về các đại lượng liên quan và cách tính toán trong chuyển động thẳng đều, hỗ trợ trong việc giải quyết các bài tập vật lý một cách hiệu quả.

Để hiểu rõ hơn về chuyển động thẳng đều, chúng ta cần xem xét các đồ thị liên quan đến chuyển động này. Đồ thị giúp trực quan hóa các đại lượng vật lý và mối quan hệ giữa chúng.

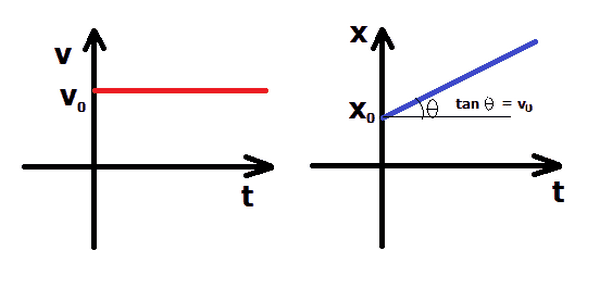
1. Đồ thị vận tốc - thời gian (v-t)

Đồ thị vận tốc theo thời gian trong chuyển động thẳng đều là một đường thẳng song song với trục thời gian. Điều này cho thấy rằng vận tốc của vật không thay đổi theo thời gian.

Ví dụ, nếu vật chuyển động với vận tốc không đổi là \( v \), đồ thị sẽ là:

Trong đó:

• \( v \) là vận tốc không đổi
• \( t \) là thời gian

2. Đồ thị tọa độ - thời gian (x-t)

Đồ thị tọa độ theo thời gian trong chuyển động thẳng đều là một đường thẳng. Độ dốc của đường thẳng biểu thị vận tốc của vật.

Phương trình đồ thị tọa độ - thời gian được cho bởi:

Trong đó:

• \( x(t) \) là tọa độ của vật tại thời điểm \( t \)
• \( x_0 \) là tọa độ ban đầu
• \( v \) là vận tốc không đổi
• \( t \) là thời gian

Ví dụ:

Giả sử một vật bắt đầu chuyển động từ vị trí \( x_0 = 0 \) với vận tốc \( v = 5 \, \text{m/s} \). Đồ thị tọa độ theo thời gian sẽ có dạng:

Đây là một đường thẳng với độ dốc 5, biểu thị rằng vật di chuyển được 5 mét mỗi giây.

Nhìn chung, đồ thị là công cụ hữu ích giúp ta hiểu rõ hơn về các đặc điểm của chuyển động thẳng đều, từ đó dễ dàng áp dụng vào việc giải các bài toán thực tế.