Các Dạng Bài Tập Chuyển Động Thẳng Đều: Hướng Dẫn Từ Cơ Bản Đến Nâng Cao

Chuyển động thẳng đều là một trong những chủ đề quan trọng trong chương trình Vật lý lớp 10. Nó bao gồm các bài tập liên quan đến sự di chuyển của vật thể với vận tốc không đổi. Dưới đây là tổng hợp các dạng bài tập phổ biến và phương pháp giải chi tiết.

I. Tổng Quan Về Chuyển Động Thẳng Đều

• Định nghĩa: Chuyển động thẳng đều là chuyển động có quỹ đạo là đường thẳng và vật có vận tốc không đổi theo thời gian.
• Công thức vận tốc: \( v = \frac{s}{t} \) với \( s \) là quãng đường di chuyển, \( t \) là thời gian di chuyển.

II. Các Dạng Bài Tập Chuyển Động Thẳng Đều

1. Dạng 1: Tính vận tốc trung bình
   • Bài tập yêu cầu tính vận tốc trung bình của một vật di chuyển trong một khoảng thời gian nhất định.
   • Công thức áp dụng: \( v_{tb} = \frac{s}{t} \)
2. Dạng 2: Tính quãng đường
   • Xác định quãng đường mà vật đã di chuyển dựa trên thời gian và vận tốc.
   • Công thức: \( s = v \cdot t \)
3. Dạng 3: Tính thời gian di chuyển
   • Tìm thời gian mà vật cần để di chuyển một quãng đường nhất định với vận tốc không đổi.
   • Công thức: \( t = \frac{s}{v} \)
4. Dạng 4: Bài tập liên quan đến đồ thị chuyển động
   • Phân tích đồ thị vận tốc - thời gian hoặc quãng đường - thời gian để tìm các đại lượng như vận tốc, quãng đường, và thời gian.

III. Phương Pháp Giải Bài Tập Chuyển Động Thẳng Đều

1. Bước 1: Đọc kỹ đề bài và xác định các thông tin đã cho: quãng đường, thời gian, vận tốc, hoặc các dữ liệu khác.
2. Bước 2: Áp dụng công thức phù hợp để giải quyết vấn đề.
3. Bước 3: Kiểm tra lại kết quả và đảm bảo rằng các đơn vị đo lường là chính xác.

IV. Ví Dụ Minh Họa

Giả sử một ô tô di chuyển trên đường thẳng với vận tốc không đổi \( v = 60 \, km/h \). Hãy tính quãng đường mà ô tô đi được trong \( 2 \, h \).

• Giải: Sử dụng công thức \( s = v \cdot t \)
• Thay số: \( s = 60 \cdot 2 = 120 \, km \)
• Vậy, ô tô di chuyển được quãng đường 120 km trong 2 giờ.

V. Kết Luận

Các dạng bài tập về chuyển động thẳng đều giúp học sinh nắm vững khái niệm cơ bản về vận tốc, quãng đường, và thời gian. Việc luyện tập và nắm chắc phương pháp giải sẽ giúp học sinh đạt được kết quả cao trong các kỳ thi.

Chuyển động thẳng đều là chuyển động của một vật theo một đường thẳng với vận tốc không đổi theo thời gian. Đặc điểm chính của chuyển động này là vật di chuyển quãng đường bằng nhau trong những khoảng thời gian bằng nhau, không phụ thuộc vào thời gian hay điểm bắt đầu.

Phương trình tổng quát của chuyển động thẳng đều có dạng:

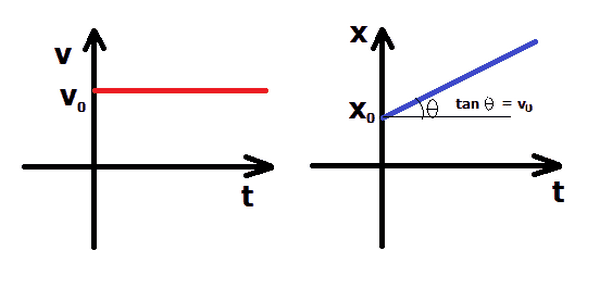
• Phương trình tọa độ: \( x = x_0 + vt \), trong đó:
• \( x \): Vị trí của vật tại thời điểm \( t \)
• \( x_0 \): Vị trí ban đầu của vật tại thời điểm \( t = 0 \)
• \( v \): Vận tốc của vật (không đổi)
• \( t \): Thời gian chuyển động

Đối với chuyển động thẳng đều, đồ thị của phương trình tọa độ theo thời gian là một đường thẳng. Sự dốc của đường thẳng này biểu thị vận tốc của vật; nếu vận tốc dương, đường thẳng đi lên, nếu vận tốc âm, đường thẳng đi xuống.

Chuyển động thẳng đều có những đặc điểm sau:

1. Vận tốc không đổi: Vận tốc của vật không thay đổi theo thời gian, nghĩa là gia tốc của vật bằng 0. Công thức tính vận tốc là: \[ v = \frac{s}{t} \], trong đó \( s \) là quãng đường đi được và \( t \) là thời gian.
2. Quãng đường di chuyển tỷ lệ thuận với thời gian: Quãng đường mà vật di chuyển được xác định bởi công thức: \[ s = v \cdot t \].
3. Phương trình chuyển động: Để xác định vị trí của vật tại bất kỳ thời điểm nào, ta sử dụng phương trình chuyển động: \( x = x_0 + vt \).

Ví dụ minh họa:

Chuyển động thẳng đều là một dạng chuyển động cơ bản trong vật lý, và các bài tập về chuyển động này thường được phân loại thành nhiều dạng khác nhau để giúp học sinh hiểu rõ các khái niệm cũng như áp dụng vào thực tế. Dưới đây là các dạng bài tập phổ biến về chuyển động thẳng đều:

• Dạng 1: Tính toán vận tốc, quãng đường và thời gian
  • Sử dụng các công thức cơ bản như:
  • Công thức tính quãng đường: \(s = v \cdot t\)
  • Công thức tính vận tốc trung bình: \[ v_{tb} = \dfrac{s}{t} = \dfrac{s_1 + s_2 + ... + s_n}{t_1 + t_2 + ... + t_n} \]
  • Ví dụ: Một chiếc xe di chuyển trong 6 giờ với 2 giờ đầu vận tốc 60 km/h và 4 giờ sau với vận tốc 40 km/h. Tính vận tốc trung bình của xe trong suốt thời gian chuyển động.
  • Hướng dẫn giải:
    1. Quãng đường đi trong 2 giờ đầu: \(s_1 = v_1 \cdot t_1 = 60 \cdot 2 = 120\) km
    2. Quãng đường đi trong 4 giờ sau: \(s_2 = v_2 \cdot t_2 = 40 \cdot 4 = 160\) km
    3. Tổng quãng đường: \(s = s_1 + s_2 = 120 + 160 = 280\) km
    4. Vận tốc trung bình: \[ v_{tb} = \dfrac{s}{t} = \dfrac{280}{6} \approx 46.67 \, \text{km/h} \]
• Dạng 2: Viết phương trình chuyển động và xác định vị trí gặp nhau của hai vật
  • Bước 1: Chọn hệ quy chiếu phù hợp.
  • Bước 2: Xác định các yếu tố ban đầu của vật: tọa độ ban đầu \((x_0)\), vận tốc \((v_0)\), thời gian ban đầu \((t_0)\).
  • Bước 3: Viết phương trình chuyển động:
  • Nếu \[ t_0 = 0 \Rightarrow x = x_0 + vt \]
  • Nếu \[ t_0 \ne 0 \Rightarrow x = x_0 + v(t - t_0) \]
  • Lưu ý:
    • Vận tốc dương nếu vật chuyển động cùng chiều dương của hệ quy chiếu.
    • Vận tốc âm nếu vật chuyển động ngược chiều dương của hệ quy chiếu.
  • Xác định thời điểm và vị trí gặp nhau của hai vật:
    1. Lập phương trình chuyển động cho mỗi vật.
    2. Giải phương trình để tìm thời điểm và vị trí mà hai vật gặp nhau.

Các dạng bài tập trên giúp học sinh nắm vững hơn về cách tính toán và áp dụng kiến thức về chuyển động thẳng đều trong các bài toán thực tế.

Để giải quyết các dạng bài tập về chuyển động thẳng đều, chúng ta cần áp dụng các phương pháp cơ bản nhưng hiệu quả. Dưới đây là các bước chi tiết để tiếp cận và giải quyết từng dạng bài tập:

3.1 Phương Pháp Giải Bài Tập Xác Định Quãng Đường và Thời Gian

Khi giải bài tập xác định quãng đường \(s\) và thời gian \(t\), chúng ta thường áp dụng công thức cơ bản:

\[
s = v \cdot t
\]

Trong đó:

• \(s\) là quãng đường vật di chuyển
• \(v\) là vận tốc
• \(t\) là thời gian di chuyển

Các bước thực hiện:

1. Xác định rõ các giá trị đã biết (vận tốc, thời gian, quãng đường).
2. Sử dụng công thức trên để tìm giá trị còn lại.
3. Kiểm tra đơn vị đo và thực hiện chuyển đổi nếu cần thiết.

3.2 Phương Pháp Giải Bài Tập Xác Định Vận Tốc Trung Bình

Để xác định vận tốc trung bình \(v_{tb}\) của vật, ta sử dụng công thức:

\[
v_{tb} = \frac{s_{total}}{t_{total}}
\]

Trong đó:

• \(s_{total}\) là tổng quãng đường di chuyển
• \(t_{total}\) là tổng thời gian di chuyển

Các bước thực hiện:

1. Tính tổng quãng đường di chuyển \(s_{total}\).
2. Tính tổng thời gian \(t_{total}\).
3. Sử dụng công thức để tìm vận tốc trung bình \(v_{tb}\).

3.3 Phương Pháp Giải Bài Tập Tìm Vị Trí và Thời Điểm Gặp Nhau

Để tìm thời điểm và vị trí gặp nhau của hai vật chuyển động thẳng đều, chúng ta áp dụng phương pháp thiết lập hệ phương trình:

Giả sử hai vật có phương trình chuyển động lần lượt là:

\[
x_1 = v_1 \cdot t + x_{01}
\]

\[
x_2 = v_2 \cdot t + x_{02}
\]

Ta có:

• \(x_1\) và \(x_2\) là vị trí của hai vật tại thời điểm \(t\).
• \(v_1\) và \(v_2\) là vận tốc của hai vật.
• \(x_{01}\) và \(x_{02}\) là vị trí ban đầu của hai vật.

Để tìm thời điểm gặp nhau \(t_{gặp}\), ta giải hệ phương trình:

\[
v_1 \cdot t_{gặp} + x_{01} = v_2 \cdot t_{gặp} + x_{02}
\]

Từ đó tính ra \(t_{gặp}\) và vị trí gặp nhau \(x_{gặp}\).

3.4 Phương Pháp Vẽ Đồ Thị Chuyển Động

Để vẽ đồ thị chuyển động thẳng đều, cần thực hiện các bước sau:

1. Xác định dạng đồ thị cần vẽ: Đồ thị vị trí - thời gian hay vận tốc - thời gian.
2. Xác định các điểm mốc trên đồ thị dựa trên dữ liệu bài toán.
3. Vẽ đồ thị với các điểm đã xác định, đảm bảo đúng tỉ lệ và mối quan hệ giữa các đại lượng.

3.5 Phương Pháp Tính Tương Đối Của Chuyển Động

Để tính chuyển động tương đối của hai vật, sử dụng công thức:

\[
v_{AB} = v_A - v_B
\]

Trong đó:

• \(v_{AB}\) là vận tốc tương đối của vật A so với vật B.
• \(v_A\) và \(v_B\) là vận tốc của hai vật so với mặt đất.

Thực hiện các bước:

1. Xác định vận tốc của từng vật.
2. Sử dụng công thức để tính vận tốc tương đối.

Dưới đây là một số ví dụ minh họa và lời giải chi tiết cho các bài tập về chuyển động thẳng đều. Những ví dụ này giúp học sinh nắm vững kiến thức lý thuyết và cách áp dụng vào giải quyết các dạng bài tập cụ thể.

Ví dụ 1: Tính vận tốc trung bình của một chiếc xe

Một chiếc xe ô tô di chuyển trên một quãng đường thẳng với quãng đường \(s = 150 \, \text{km}\) trong thời gian \(t = 3 \, \text{giờ}\). Hãy tính vận tốc trung bình của chiếc xe.

Lời giải:

Sử dụng công thức tính vận tốc trung bình:

Thay các giá trị đã cho vào công thức:

Vậy vận tốc trung bình của chiếc xe là \(50 \, \text{km/h}\).

Ví dụ 2: Tính quãng đường đi được

Một vật chuyển động thẳng đều với vận tốc \(v = 20 \, \text{m/s}\) trong thời gian \(t = 10 \, \text{giây}\). Hãy tính quãng đường vật đã đi được.

Lời giải:

Sử dụng công thức tính quãng đường:

Thay các giá trị đã cho vào công thức:

Vậy quãng đường vật đã đi được là \(200 \, \text{m}\).

Ví dụ 3: Xác định thời gian chuyển động

Một người đi bộ với vận tốc \(v = 4 \, \text{km/h}\) trên một quãng đường dài \(s = 10 \, \text{km}\). Hãy xác định thời gian người đó hoàn thành quãng đường.

Lời giải:

Sử dụng công thức tính thời gian:

Thay các giá trị đã cho vào công thức:

Vậy thời gian người đó cần để hoàn thành quãng đường là \(2.5 \, \text{giờ}\).

Khi làm bài tập về chuyển động thẳng đều, để đạt được kết quả tốt nhất và tránh những sai sót, bạn cần lưu ý các điểm sau:

• Xác định rõ hệ quy chiếu: Đảm bảo bạn đã chọn đúng hệ quy chiếu và xác định gốc tọa độ cũng như gốc thời gian. Điều này là cơ bản nhưng cực kỳ quan trọng để tránh nhầm lẫn trong quá trình giải.
• Kiểm tra đơn vị: Luôn kiểm tra kỹ các đơn vị đo lường như thời gian (giờ, phút, giây), quãng đường (km, m), và vận tốc (km/h, m/s). Nếu cần thiết, chuyển đổi các đơn vị này về cùng một hệ thống trước khi bắt đầu giải bài.
• Sử dụng phương trình chuyển động đúng: Phương trình chuyển động thẳng đều có dạng \(x = x_0 + vt\). Hãy chắc chắn rằng bạn áp dụng đúng phương trình cho từng phần bài tập, đặc biệt khi có nhiều giai đoạn chuyển động khác nhau.
• Phân tích kỹ đề bài: Đọc kỹ đề bài để hiểu rõ các yếu tố quan trọng như vị trí ban đầu, thời gian và vận tốc. Nếu có nhiều đối tượng tham gia chuyển động, bạn cần lập phương trình chuyển động riêng cho từng đối tượng.
• Kiểm tra kết quả: Sau khi giải xong, kiểm tra lại các bước và đảm bảo kết quả có ý nghĩa vật lý. Ví dụ, thời gian không thể âm, vận tốc không thể vượt quá giới hạn hợp lý trong bối cảnh bài toán.
• Đừng quên các yếu tố thực tế: Một số bài toán yêu cầu bạn phải tính đến các yếu tố thực tế như gia tốc, ma sát, hay lực cản. Hãy đọc kỹ đề bài để không bỏ sót những yếu tố này.

Bằng cách tuân thủ những lưu ý này, bạn sẽ nâng cao khả năng giải quyết các bài tập về chuyển động thẳng đều một cách hiệu quả và chính xác hơn.

Chuyển động thẳng đều là một trong những khái niệm cơ bản trong vật lý, đóng vai trò quan trọng trong việc hiểu về cách vật thể di chuyển. Bằng cách nắm vững các công thức và phương pháp giải bài tập liên quan đến chuyển động thẳng đều, học sinh có thể giải quyết các vấn đề phức tạp hơn trong thực tế. Điều quan trọng là luôn chú ý đến việc chọn hệ quy chiếu và xác định các đại lượng cần thiết trước khi áp dụng công thức.

Việc luyện tập thường xuyên với các dạng bài tập khác nhau sẽ giúp học sinh nâng cao kỹ năng và tự tin hơn khi đối mặt với các bài toán chuyển động. Hãy luôn ghi nhớ những lưu ý quan trọng, kiểm tra kỹ lưỡng các bước giải để tránh những sai sót không đáng có.

Cuối cùng, hãy luôn duy trì sự tập trung và tinh thần ham học hỏi để không ngừng nâng cao kiến thức vật lý của mình.