Hai Ô Tô Chuyển Động Thẳng Đều: Phân Tích, Ứng Dụng Và Bài Tập Thực Tế

Chuyển động thẳng đều là chuyển động có quãng đường tỉ lệ thuận với thời gian. Điều này có nghĩa là trong cùng một khoảng thời gian, hai ô tô di chuyển được các quãng đường bằng nhau nếu chúng duy trì vận tốc không đổi.

Phương trình chuyển động

Phương trình chuyển động thẳng đều được viết dưới dạng:

\[x = x_0 + v \cdot t\]

Trong đó:

• x: vị trí của ô tô tại thời điểm t.
• x_0: vị trí ban đầu của ô tô.
• v: vận tốc của ô tô.
• t: thời gian di chuyển.

Ví dụ về hai ô tô di chuyển thẳng đều

Giả sử hai ô tô xuất phát từ hai điểm cách nhau 120 km và chuyển động thẳng đều ngược chiều với vận tốc tương ứng là 40 km/h và 20 km/h. Sau 2 giờ, hai xe sẽ gặp nhau.

Tính vận tốc của hai ô tô

Vận tốc của xe thứ nhất (\(v_1\)) và xe thứ hai (\(v_2\)) có thể được liên kết với nhau bằng mối quan hệ:

\[v_1 = 1,2 \cdot v_2\]

Do hai xe đi ngược chiều nên khoảng cách rút ngắn giữa chúng sau mỗi giờ sẽ là tổng vận tốc của cả hai:

\[v_1 + v_2 = 1,2 \cdot v_2 + v_2 = 2,2 \cdot v_2\]

Bài toán tìm thời điểm gặp nhau

Khi hai ô tô di chuyển ngược chiều với quãng đường ban đầu giữa chúng là 120 km, thời gian để hai xe gặp nhau là:

\[t = \frac{120}{v_1 + v_2} = \frac{120}{2,2 \cdot v_2}\]

Từ đó, ta có thể tìm ra vận tốc của xe thứ hai và vận tốc của xe thứ nhất.

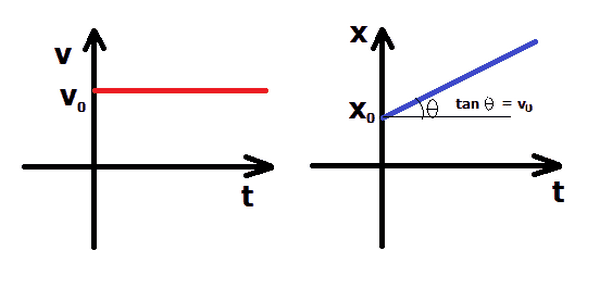
Đồ thị chuyển động

Trong chuyển động thẳng đều, đồ thị biểu diễn giữa quãng đường và thời gian là một đường thẳng dốc lên. Độ dốc của đường thẳng chính là vận tốc của ô tô.

Bài tập minh họa

1. Một ô tô khởi hành từ điểm A với vận tốc 60 km/h và ô tô thứ hai khởi hành từ điểm B với vận tốc 40 km/h. Hãy tính vị trí mà hai ô tô gặp nhau.
2. Hai ô tô cùng khởi hành ngược chiều nhau và vận tốc của xe thứ nhất gấp 1,2 lần vận tốc của xe thứ hai. Sau 2 giờ, hai xe gặp nhau. Tính vận tốc của từng xe.

Chuyển động thẳng đều là loại chuyển động mà trong đó vật di chuyển theo một đường thẳng và vận tốc của nó không thay đổi theo thời gian. Điều này có nghĩa là quãng đường vật di chuyển được trong những khoảng thời gian bằng nhau luôn luôn bằng nhau.

• Quỹ đạo chuyển động: Đường thẳng.
• Vận tốc: Không đổi, nghĩa là giá trị vận tốc \[v\] của vật không thay đổi theo thời gian.
• Phương trình chuyển động thẳng đều: \[ x = x_0 + v \cdot t \] Trong đó:
  • \(x\): Tọa độ của vật tại thời điểm \(t\).
  • \(x_0\): Tọa độ ban đầu của vật.
  • \(v\): Vận tốc của vật.
  • \(t\): Thời gian chuyển động.
• Chú ý:
  • Nếu \(v > 0\), vật chuyển động theo chiều dương của trục tọa độ.
  • Nếu \(v < 0\), vật chuyển động theo chiều âm của trục tọa độ.

Trong chuyển động thẳng đều, vận tốc của vật thể không thay đổi theo thời gian. Phương trình chuyển động thẳng đều thể hiện mối quan hệ giữa vị trí của vật theo thời gian và được viết dưới dạng:

\[
x = x_0 + v \cdot t
\]

Trong đó:

• \(x\): Vị trí của vật tại thời điểm \(t\) (đơn vị: mét).
• \(x_0\): Vị trí ban đầu của vật tại thời điểm \(t = 0\) (đơn vị: mét).
• \(v\): Vận tốc của vật (đơn vị: mét/giây).
• \(t\): Thời gian chuyển động (đơn vị: giây).

Phương trình này biểu thị rằng vị trí của vật thay đổi đều đặn theo thời gian với vận tốc không đổi.

Nếu vận tốc \(v > 0\), vật chuyển động theo chiều dương của trục tọa độ; ngược lại, nếu \(v < 0\), vật chuyển động theo chiều âm.

Ví dụ: Một ô tô chuyển động thẳng đều với vận tốc \(v = 10 \, m/s\), xuất phát từ vị trí \(x_0 = 5 \, m\). Phương trình chuyển động của ô tô là:

\[
x = 5 + 10 \cdot t
\]

Với phương trình này, ta có thể tính được vị trí của ô tô tại mọi thời điểm trong quá trình chuyển động.

Trong bài toán này, chúng ta xét hai ô tô đang chuyển động thẳng đều trên cùng một đường với các thông số cho trước. Mỗi ô tô có một vận tốc riêng và xuất phát từ các vị trí khác nhau. Mục tiêu của bài toán là xác định thời điểm và vị trí mà hai ô tô gặp nhau.

Giả sử ô tô thứ nhất có vận tốc \(v_1\), xuất phát từ vị trí \(x_1\) và ô tô thứ hai có vận tốc \(v_2\), xuất phát từ vị trí \(x_2\). Phương trình chuyển động của mỗi ô tô được cho bởi:

• Phương trình chuyển động của ô tô thứ nhất: \[x_1(t) = x_{1_0} + v_1 \cdot t\]
• Phương trình chuyển động của ô tô thứ hai: \[x_2(t) = x_{2_0} + v_2 \cdot t\]

Để tìm thời điểm hai ô tô gặp nhau, ta cần giải phương trình:

\[
x_1(t) = x_2(t)
\]

Thay phương trình chuyển động của từng ô tô vào, ta có:

\[
x_{1_0} + v_1 \cdot t = x_{2_0} + v_2 \cdot t
\]

Sau khi đơn giản hóa, ta tìm được thời điểm gặp nhau:

\[
t = \frac{x_{2_0} - x_{1_0}}{v_1 - v_2}
\]

Điều kiện để hai ô tô gặp nhau là \(v_1 \neq v_2\) và \(x_{2_0} - x_{1_0}\) cùng dấu với \(v_1 - v_2\).

Ví dụ: Nếu ô tô thứ nhất có vận tốc \(v_1 = 60 \, km/h\) và xuất phát từ vị trí \(x_{1_0} = 0 \, km\), trong khi ô tô thứ hai có vận tốc \(v_2 = 40 \, km/h\) và xuất phát từ vị trí \(x_{2_0} = 100 \, km\), thời gian hai ô tô gặp nhau sẽ là:

\[
t = \frac{100 - 0}{60 - 40} = 5 \, giờ
\]

Sau 5 giờ, hai ô tô sẽ gặp nhau tại vị trí:

\[
x = x_{1_0} + v_1 \cdot t = 0 + 60 \cdot 5 = 300 \, km
\]

Như vậy, hai ô tô gặp nhau tại vị trí cách điểm xuất phát của ô tô thứ nhất 300 km.

Chuyển động thẳng đều là một khái niệm cơ bản trong vật lý, có nhiều ứng dụng thực tiễn trong cuộc sống hàng ngày và các ngành công nghiệp khác nhau. Dưới đây là một số ứng dụng cụ thể của chuyển động thẳng đều:

• Giao thông vận tải: Trong giao thông, chuyển động thẳng đều được sử dụng để mô phỏng và dự đoán hành vi của các phương tiện trên đường. Điều này giúp tối ưu hóa việc quản lý giao thông và dự báo thời gian hành trình.
• Hàng không: Trong hàng không, việc tính toán các giai đoạn chuyển động thẳng đều của máy bay giúp tối ưu hóa việc tiêu thụ nhiên liệu và quản lý khoảng cách giữa các máy bay trong không phận.
• Robot học: Trong ngành robot, chuyển động thẳng đều được sử dụng để lập trình các robot di chuyển với tốc độ không đổi, giúp nâng cao độ chính xác và hiệu quả trong quá trình vận hành.
• Kiến trúc và xây dựng: Việc mô phỏng chuyển động thẳng đều của các phương tiện xây dựng giúp tối ưu hóa quá trình vận chuyển vật liệu và quản lý an toàn lao động.

Một ví dụ cụ thể là trong hệ thống giao thông công cộng, việc xác định chính xác thời gian và khoảng cách giữa các phương tiện chuyển động thẳng đều trên cùng một tuyến đường giúp cải thiện sự điều phối và giảm ùn tắc giao thông.

Chuyển động thẳng đều cũng là một phần quan trọng trong các mô phỏng khoa học, giúp nghiên cứu và giải quyết các vấn đề trong nhiều lĩnh vực từ cơ học, hàng không, đến quản lý năng lượng.

Dưới đây là một số bài tập và câu hỏi trắc nghiệm giúp các bạn củng cố kiến thức về chuyển động thẳng đều, đặc biệt trong bài toán hai ô tô chuyển động thẳng đều.

• Bài tập 1: Hai ô tô chuyển động thẳng đều trên một đường thẳng. Ô tô A có vận tốc \(v_A = 60 \, \text{km/h}\), ô tô B có vận tốc \(v_B = 40 \, \text{km/h}\). Sau bao lâu khoảng cách giữa hai xe là 100 km nếu ban đầu chúng cùng xuất phát?
• Bài tập 2: Một ô tô chuyển động thẳng đều với vận tốc \(v = 80 \, \text{km/h}\). Tính thời gian để xe di chuyển được quãng đường 160 km.
• Bài tập 3: Ô tô A và B xuất phát từ cùng một điểm với vận tốc lần lượt là \(v_A = 70 \, \text{km/h}\) và \(v_B = 50 \, \text{km/h}\). Sau 2 giờ, khoảng cách giữa hai ô tô là bao nhiêu?
• Bài tập 4: Hai xe chuyển động thẳng đều trên cùng một đoạn đường với các vận tốc khác nhau. Nếu sau 3 giờ, khoảng cách giữa chúng là 90 km, hãy tính vận tốc của mỗi xe biết rằng chúng khởi hành cùng lúc.

Câu hỏi trắc nghiệm:

1. Chuyển động thẳng đều là chuyển động có đặc điểm nào sau đây?
   • a. Vận tốc không thay đổi
   • b. Gia tốc thay đổi
   • c. Quãng đường đi được tỉ lệ thuận với thời gian
   • d. Cả a và c
2. Phương trình chuyển động thẳng đều có dạng:
   • a. \(x = x_0 + vt\)
   • b. \(x = x_0 + \frac{1}{2}at^2\)
   • c. \(v = v_0 + at\)
   • d. \(x = v_0 + v\)
3. Với vận tốc không đổi, quãng đường đi được trong chuyển động thẳng đều tỉ lệ thuận với:
   • a. Thời gian
   • b. Gia tốc
   • c. Khối lượng
   • d. Lực tác dụng