Bài Tập Giao Thoa Ánh Sáng Hay Và Khó - Tổng Hợp Những Dạng Bài Tập Thách Thức Nhất

Giao thoa ánh sáng là một hiện tượng vật lý quan trọng và thường xuất hiện trong các đề thi vật lý từ cấp trung học phổ thông đến đại học. Dưới đây là tổng hợp những bài tập giao thoa ánh sáng hay và khó, giúp các bạn học sinh và sinh viên ôn tập và rèn luyện kỹ năng giải bài tập.

1. Bài tập trắc nghiệm giao thoa ánh sáng

• Trong thí nghiệm Y-âng về giao thoa ánh sáng, khe hẹp S phát ra đồng thời ba bức xạ đơn sắc có bước sóng là \(\lambda_{1} = 0,42 \, \mu m\), \(\lambda_{2} = 0,56 \, \mu m\), và \(\lambda_{3} = 0,63 \, \mu m\). Tính số vân sáng quan sát được.
• Bài tập về sự giao thoa ánh sáng với hai khe Young khi chiếu đồng thời hai bức xạ đơn sắc có bước sóng \(\lambda_{1} = 0,6 \, \mu m\) và \(\lambda_{2} = 0,4 \, \mu m\) vào khe Y – âng.

2. Phương pháp giải bài tập giao thoa ánh sáng

• Sử dụng phương pháp khoảng vân \(\Delta x = \dfrac{\lambda \times D}{a}\) để tính toán khoảng cách giữa các vân sáng và vân tối trên màn quan sát.
• Áp dụng công thức tính vị trí vân sáng \(x_k = k \times \Delta x\) để xác định tọa độ của vân sáng thứ \(k\).

3. Bài tập tự luyện giao thoa ánh sáng

Các bài tập tự luyện dưới đây giúp bạn kiểm tra và củng cố kiến thức về giao thoa ánh sáng:

1. Cho một thí nghiệm Y-âng với ánh sáng đơn sắc có bước sóng \(\lambda = 0,5 \, \mu m\), khoảng cách giữa hai khe là \(a = 0,5 \, mm\) và khoảng cách từ hai khe đến màn quan sát là \(D = 1 \, m\). Tính khoảng vân và vị trí vân sáng thứ 5.
2. Trong thí nghiệm Y-âng, chiếu ánh sáng trắng (bước sóng từ \(0,4 \, \mu m\) đến \(0,76 \, \mu m\)) vào hai khe Y-âng. Bức xạ nào không tạo vân sáng tại điểm cách vân trung tâm \(5,4 \, mm\)?

4. Các dạng bài tập giao thoa ánh sáng khó

Những bài tập dưới đây yêu cầu sự kết hợp nhiều kiến thức và kỹ năng tính toán:

• Thí nghiệm Y-âng với nhiều nguồn sáng có bước sóng khác nhau, yêu cầu tính số vân sáng trùng nhau và khoảng cách giữa các vân sáng đó.
• Bài toán liên quan đến dịch chuyển màn quan sát để thay đổi khoảng vân.

5. Lợi ích của việc luyện tập bài tập giao thoa ánh sáng

Luyện tập các bài tập giao thoa ánh sáng không chỉ giúp bạn nắm vững kiến thức lý thuyết mà còn phát triển tư duy logic, khả năng phân tích và giải quyết vấn đề. Điều này rất hữu ích trong các kỳ thi quan trọng như thi tốt nghiệp THPT và thi đại học.

Chúc các bạn học tốt và đạt kết quả cao trong các kỳ thi!

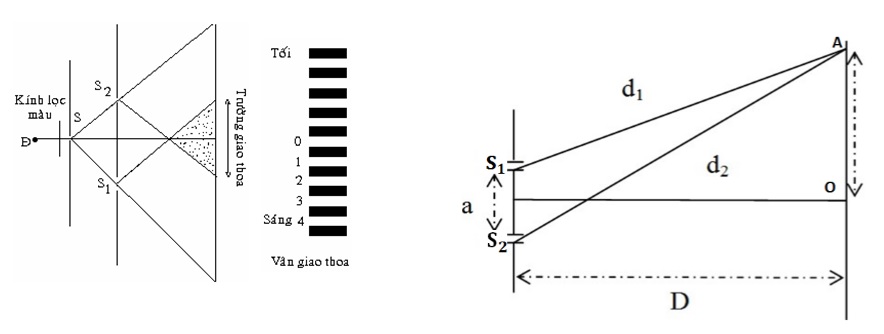
Giao thoa ánh sáng là một hiện tượng xảy ra khi hai hay nhiều sóng ánh sáng kết hợp với nhau tạo thành những vùng sáng tối xen kẽ. Đây là một hiện tượng đặc trưng của sóng, cho thấy ánh sáng có tính chất sóng. Khi hai sóng ánh sáng gặp nhau, chúng có thể tăng cường hoặc triệt tiêu lẫn nhau, tạo ra những vân sáng và vân tối.

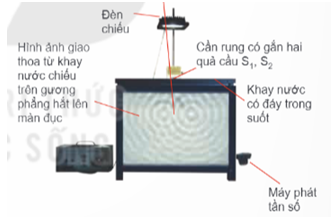
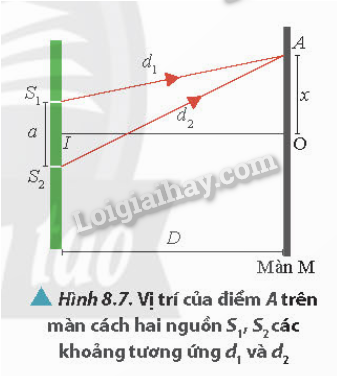
Thí nghiệm Y-âng là một trong những thí nghiệm nổi tiếng minh chứng cho hiện tượng giao thoa ánh sáng. Trong thí nghiệm này, ánh sáng từ một nguồn sáng đơn sắc chiếu qua hai khe hẹp song song, tạo ra hai chùm sóng ánh sáng lan truyền và giao thoa với nhau trên màn quan sát phía sau. Các vân sáng, vân tối được hình thành do sự giao thoa này.

Công thức cơ bản để tính khoảng vân trong hiện tượng giao thoa ánh sáng được cho bởi:

Trong đó:

• \(\lambda\) là bước sóng của ánh sáng.
• \(D\) là khoảng cách từ hai khe đến màn quan sát.
• \(a\) là khoảng cách giữa hai khe.

Khoảng vân \(i\) là khoảng cách giữa hai vân sáng hoặc hai vân tối liên tiếp. Đây là yếu tố quan trọng để xác định vị trí các vân trên màn quan sát.

Hiện tượng giao thoa ánh sáng không chỉ xảy ra với ánh sáng đơn sắc mà còn với ánh sáng trắng, tuy nhiên, các vân giao thoa sẽ bị trải ra thành dải màu do sự khác biệt về bước sóng của các bức xạ đơn sắc trong ánh sáng trắng.

Dưới đây là một số bài tập cơ bản về giao thoa ánh sáng, giúp bạn nắm vững các khái niệm và phương pháp giải quyết các vấn đề liên quan đến hiện tượng này.

1. Bài tập 1: Tính khoảng vân

   Hai khe hẹp cách nhau một khoảng \(a = 0.5 \, mm\) được chiếu sáng bằng ánh sáng đơn sắc có bước sóng \(\lambda = 600 \, nm\). Màn quan sát đặt cách hai khe \(D = 2 \, m\). Tính khoảng vân giao thoa \(i\) trên màn.

   \[ i = \frac{\lambda D}{a} \]
2. Bài tập 2: Vị trí của vân sáng thứ 3

   Với các thông số như ở Bài tập 1, hãy tính vị trí của vân sáng thứ 3 trên màn quan sát.

   \[ x_3 = 3 \cdot i \]
3. Bài tập 3: Số vân sáng quan sát được

   Cho biết chiều rộng của màn quan sát là \(L = 1 \, m\). Tính số lượng vân sáng quan sát được trên màn.

   \[ N = \frac{2L}{i} \]
4. Bài tập 4: Khoảng cách giữa hai vân sáng liền kề

   Với các thông số đã cho, hãy tính khoảng cách giữa hai vân sáng liền kề trên màn quan sát.

   \[ \Delta x = i \]
5. Bài tập 5: Tính vị trí vân tối thứ 2

   Với các thông số như Bài tập 1, hãy tính vị trí của vân tối thứ 2 trên màn quan sát.

   \[ x_2 = (2 + \frac{1}{2}) \cdot i \]
6. Bài tập 6: Giao thoa với ánh sáng trắng

   Nếu thay ánh sáng đơn sắc bằng ánh sáng trắng, hãy mô tả hiện tượng giao thoa trên màn và tính khoảng cách giữa các vân sáng của ánh sáng có bước sóng ngắn nhất và dài nhất.

7. Bài tập 7: Ảnh hưởng của việc thay đổi khoảng cách giữa hai khe

   Nếu khoảng cách giữa hai khe \(a\) được tăng lên, hãy mô tả sự thay đổi của khoảng vân \(i\) và số lượng vân sáng quan sát được.

8. Bài tập 8: Ảnh hưởng của việc thay đổi bước sóng ánh sáng

   Nếu bước sóng của ánh sáng tăng lên, hãy mô tả sự thay đổi của khoảng vân và vị trí các vân sáng.

9. Bài tập 9: Vị trí vân tối trung tâm

   Trong trường hợp có sự dịch chuyển nhỏ giữa hai khe, hãy tính vị trí của vân tối trung tâm trên màn.

10. Bài tập 10: Tính khoảng cách giữa hai vân tối liền kề

    Hãy tính khoảng cách giữa hai vân tối liền kề trong các trường hợp khác nhau về khoảng cách khe và bước sóng ánh sáng.

Các dạng bài tập giao thoa ánh sáng nâng cao yêu cầu học sinh phải vận dụng kiến thức một cách linh hoạt và sáng tạo để giải quyết các vấn đề phức tạp hơn. Dưới đây là một số dạng bài tập phổ biến và phương pháp giải chi tiết.

1. Bài tập 1: Tính toán với nguồn sáng có nhiều bước sóng

   Cho hai khe Y-Young cách nhau \(a = 1 \, mm\), chiếu sáng bởi hai nguồn sáng có bước sóng khác nhau \(\lambda_1 = 500 \, nm\) và \(\lambda_2 = 600 \, nm\). Màn quan sát cách hai khe một khoảng \(D = 2 \, m\). Tính khoảng cách giữa các vân sáng có cùng vị trí trên màn.

   \[ \Delta x = \frac{D(\lambda_1 - \lambda_2)}{a} \]
2. Bài tập 2: Giao thoa với ánh sáng trong môi trường khác nhau

   Hai khe hẹp đặt trong môi trường có chiết suất \(n = 1.5\), chiếu sáng bởi ánh sáng đơn sắc có bước sóng \(\lambda = 600 \, nm\) trong không khí. Tính khoảng vân giao thoa khi chiết suất thay đổi.

   \[ i' = \frac{\lambda D}{a n} \]
3. Bài tập 3: Ảnh hưởng của sự dịch chuyển khe

   Nếu một trong hai khe dịch chuyển một đoạn nhỏ \(\Delta a\) theo phương ngang, hãy tính sự thay đổi vị trí các vân sáng và tối trên màn quan sát.

   \[ \Delta x = \frac{\Delta a \cdot D}{a} \]
4. Bài tập 4: Giao thoa với ánh sáng không đồng nhất

   Ánh sáng chiếu tới hai khe gồm các thành phần ánh sáng đơn sắc có bước sóng từ \(400 \, nm\) đến \(700 \, nm\). Tính sự phân bố các vân sáng trên màn quan sát.

5. Bài tập 5: Tính toán với khe hẹp có độ rộng đáng kể

   Hai khe có độ rộng \(b\) nhất định, tạo ra hiện tượng nhiễu xạ trước khi giao thoa. Tính ảnh hưởng của nhiễu xạ đến khoảng cách giữa các vân giao thoa.

6. Bài tập 6: Giao thoa với nguồn sáng mở rộng

   Nếu nguồn sáng không phải là điểm, mà có kích thước mở rộng, hãy tính sự phân bố và độ nét của các vân giao thoa trên màn.

7. Bài tập 7: Giao thoa trong trường hợp nguồn sáng bị che khuất

   Khi một phần của nguồn sáng bị che khuất bởi một vật cản, hãy tính sự thay đổi của các vân sáng và tối trên màn.

8. Bài tập 8: Hiệu ứng Doppler trong giao thoa ánh sáng

   Nếu nguồn sáng di chuyển với vận tốc \(v\) theo hướng tới hoặc ra xa khỏi khe, tính sự thay đổi của tần số ánh sáng và các vân giao thoa trên màn.

9. Bài tập 9: Giao thoa với ánh sáng laser

   Sử dụng nguồn laser để chiếu sáng hai khe, tính sự phân bố cường độ ánh sáng trên màn quan sát khi có nhiễu xạ kết hợp với giao thoa.

10. Bài tập 10: Giao thoa với ánh sáng phân cực

    Ánh sáng chiếu tới hai khe là ánh sáng phân cực. Hãy tính sự phân bố các vân sáng khi góc giữa hai vector phân cực thay đổi.

Dưới đây là 10 dạng bài tập giao thoa ánh sáng được chọn lọc kỹ lưỡng, kèm theo lời giải chi tiết. Những bài tập này sẽ giúp bạn nắm vững kiến thức và làm quen với các phương pháp giải toán liên quan đến hiện tượng giao thoa ánh sáng.

1. Dạng 1: Tính khoảng vân giao thoa

   Bài tập: Hai khe cách nhau một khoảng \(a = 0.5 \, mm\), chiếu sáng bởi ánh sáng đơn sắc có bước sóng \(\lambda = 600 \, nm\). Màn quan sát cách hai khe một khoảng \(D = 2 \, m\). Tính khoảng vân giao thoa trên màn.

   Lời giải: Khoảng vân giao thoa được tính theo công thức:

   \[ i = \frac{\lambda D}{a} = \frac{600 \times 10^{-9} \times 2}{0.5 \times 10^{-3}} = 2.4 \, mm \]
2. Dạng 2: Tìm vị trí các vân sáng và vân tối

   Bài tập: Với dữ liệu ở trên, hãy tìm vị trí của vân sáng bậc 3 và vân tối thứ 2.

   Lời giải: Vị trí vân sáng và vân tối được tính bằng công thức:

   \[ x_k = k \cdot i \quad \text{(vân sáng)}, \quad x_t = (k + \frac{1}{2}) \cdot i \quad \text{(vân tối)} \]

   Áp dụng cho \(k = 3\) và \(k = 2\):

   \[ x_3 = 3 \times 2.4 = 7.2 \, mm, \quad x_{t2} = (2 + \frac{1}{2}) \times 2.4 = 6 \, mm \]
3. Dạng 3: Tính số vân sáng giữa hai điểm

   Bài tập: Giữa hai điểm trên màn cách nhau 12 mm, có bao nhiêu vân sáng.

   Lời giải: Số vân sáng là:

   \[ N = \frac{\Delta x}{i} = \frac{12}{2.4} = 5 \, vân \]
4. Dạng 4: Giao thoa với ánh sáng có nhiều bước sóng

   Bài tập: Hai khe được chiếu sáng bởi hai nguồn sáng có bước sóng \(\lambda_1 = 500 \, nm\) và \(\lambda_2 = 700 \, nm\). Tính khoảng cách giữa các vân sáng của hai bước sóng này.

   Lời giải: Khoảng cách giữa các vân sáng:

   \[ \Delta x = \left| \frac{\lambda_1 D}{a} - \frac{\lambda_2 D}{a} \right| = \left| \frac{500 \times 2}{0.5} - \frac{700 \times 2}{0.5} \right| = 0.8 \, mm \]
5. Dạng 5: Ảnh hưởng của sự thay đổi khoảng cách khe

   Bài tập: Nếu khoảng cách giữa hai khe tăng lên gấp đôi, hãy tính sự thay đổi của khoảng vân giao thoa.

   Lời giải: Khi khoảng cách khe tăng lên gấp đôi, khoảng vân sẽ giảm đi một nửa:

   \[ i' = \frac{i}{2} = 1.2 \, mm \]
6. Dạng 6: Giao thoa với ánh sáng trong môi trường có chiết suất khác nhau

   Bài tập: Khi ánh sáng truyền qua môi trường có chiết suất \(n = 1.5\), tính khoảng vân.

   Lời giải: Khoảng vân giao thoa trong môi trường có chiết suất là:

   \[ i = \frac{\lambda D}{a n} = \frac{600 \times 10^{-9} \times 2}{0.5 \times 10^{-3} \times 1.5} = 1.6 \, mm \]
7. Dạng 7: Tính số vân sáng và vân tối

   Bài tập: Giữa hai điểm trên màn cách nhau 20 mm, có bao nhiêu vân sáng và vân tối?

   Lời giải: Số vân sáng và vân tối:

   \[ N_s = \frac{20}{2.4} = 8.33 \, vân \quad \text{(vân sáng)}, \quad N_t = N_s - 1 = 7.33 \, vân \quad \text{(vân tối)} \]
8. Dạng 8: Giao thoa với ánh sáng phân cực

   Bài tập: Ánh sáng chiếu tới hai khe là ánh sáng phân cực. Tính sự phân bố vân sáng khi góc giữa hai vector phân cực là \(45^\circ\).

   Lời giải: Khi góc phân cực là \(45^\circ\), cường độ ánh sáng:

   \[ I = I_0 \cos^2(45^\circ) = \frac{I_0}{2} \]
9. Dạng 9: Tính vân giao thoa trong trường hợp khe không hẹp

   Bài tập: Nếu một khe rộng hơn khe còn lại, hãy tính ảnh hưởng đến khoảng vân.

   Lời giải: Khi khe không hẹp, các vân sáng trở nên mờ nhạt và khoảng vân có thể bị biến dạng.

10. Dạng 10: Giao thoa với ánh sáng laser

    Bài tập: Sử dụng nguồn laser chiếu tới hai khe, hãy tính sự phân bố cường độ sáng trên màn quan sát.

    Lời giải: Với ánh sáng laser, cường độ ánh sáng trên màn sẽ rất mạnh và rõ nét, vân sáng sắc nét hơn.

Việc luyện tập các bài tập giao thoa ánh sáng mang lại nhiều lợi ích quan trọng cho học sinh và sinh viên, đặc biệt trong việc nắm vững các kiến thức cơ bản và nâng cao trong vật lý. Dưới đây là những lợi ích cụ thể:

• Củng cố kiến thức lý thuyết: Thông qua việc giải các bài tập, học sinh có thể ôn lại và hiểu sâu hơn về các khái niệm như khoảng vân, điều kiện giao thoa, và ứng dụng của hiện tượng giao thoa ánh sáng.
• Nâng cao kỹ năng giải quyết vấn đề: Các bài tập giao thoa ánh sáng thường yêu cầu học sinh phải suy nghĩ logic, sử dụng các công thức và phương pháp tính toán một cách chính xác. Điều này giúp rèn luyện khả năng phân tích và giải quyết vấn đề.
• Phát triển tư duy khoa học: Khi luyện tập, học sinh sẽ tiếp xúc với nhiều dạng bài tập khác nhau, từ cơ bản đến nâng cao, từ đó phát triển tư duy khoa học và khả năng tư duy sáng tạo trong việc áp dụng lý thuyết vào thực tế.
• Chuẩn bị tốt cho các kỳ thi: Việc luyện tập thường xuyên các dạng bài tập giao thoa ánh sáng giúp học sinh làm quen với các dạng câu hỏi có thể gặp trong các kỳ thi, từ đó tăng cường tự tin và hiệu quả làm bài.
• Tăng cường khả năng tự học: Qua quá trình giải bài tập, học sinh có thể phát hiện ra những lỗ hổng trong kiến thức của mình và từ đó tìm cách tự học, tự bổ sung kiến thức còn thiếu.

Nhờ những lợi ích này, việc luyện tập bài tập giao thoa ánh sáng không chỉ giúp học sinh hiểu rõ hơn về vật lý mà còn phát triển nhiều kỹ năng quan trọng khác trong học tập và cuộc sống.