Giao Thoa 3 Ánh Sáng Đơn Sắc: Khám Phá Hiện Tượng Quang Học Kỳ Thú

Giao thoa ánh sáng là một hiện tượng vật lý quan trọng trong quang học, đặc biệt khi đề cập đến giao thoa của ba ánh sáng đơn sắc. Hiện tượng này xảy ra khi ba nguồn sáng có bước sóng khác nhau chiếu vào cùng một điểm, tạo ra các vân sáng và tối. Mức độ phức tạp của hiện tượng này phụ thuộc vào sự khác biệt về bước sóng và pha của các sóng ánh sáng tham gia.

Nguyên lý cơ bản

Trong giao thoa ánh sáng, các sóng ánh sáng từ ba nguồn khác nhau kết hợp với nhau, tạo ra các vân giao thoa. Hiện tượng này có thể được mô tả bằng phương trình giao thoa tổng quát:

\[
I = I_1 + I_2 + I_3 + 2\sqrt{I_1I_2} \cos(\phi_{12}) + 2\sqrt{I_1I_3} \cos(\phi_{13}) + 2\sqrt{I_2I_3} \cos(\phi_{23})
\]

Trong đó:

• \(I\) là cường độ tổng hợp của ánh sáng tại điểm quan sát.
• \(I_1, I_2, I_3\) là cường độ của ba ánh sáng đơn sắc tương ứng.
• \(\phi_{12}, \phi_{13}, \phi_{23}\) là độ lệch pha giữa các sóng ánh sáng.

Ứng dụng của hiện tượng giao thoa

Hiện tượng giao thoa ánh sáng được ứng dụng trong nhiều lĩnh vực khoa học và công nghệ như:

• Phân tích quang phổ: Giao thoa ánh sáng giúp xác định các đặc trưng quang phổ của các nguồn sáng khác nhau.
• Kiểm tra chất lượng bề mặt: Các vân giao thoa được sử dụng để kiểm tra độ phẳng và độ nhám của bề mặt trong công nghiệp.
• Đo lường chính xác: Kỹ thuật giao thoa được sử dụng để đo các khoảng cách rất nhỏ với độ chính xác cao, chẳng hạn như trong các thí nghiệm đo bước sóng ánh sáng.

Thí nghiệm tiêu biểu

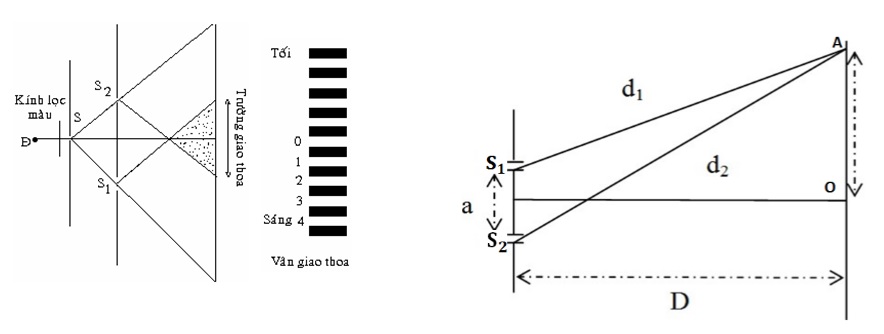
Một trong những thí nghiệm nổi tiếng về giao thoa ánh sáng là thí nghiệm Y-âng. Trong thí nghiệm này, ánh sáng đơn sắc từ một nguồn chiếu qua hai khe hẹp song song, tạo ra các vân sáng tối xen kẽ trên màn quan sát. Khi ba nguồn sáng với bước sóng khác nhau được sử dụng, các vân giao thoa phức tạp hơn, với sự xuất hiện của các vân giao thoa mới do sự tương tác của ba sóng ánh sáng.

Kết luận

Hiện tượng giao thoa của ba ánh sáng đơn sắc là một phần quan trọng trong việc nghiên cứu các tính chất của ánh sáng và ứng dụng của nó trong các ngành khoa học và công nghệ. Thông qua các thí nghiệm và ứng dụng thực tế, hiện tượng này đóng vai trò quan trọng trong việc nâng cao hiểu biết của con người về bản chất của ánh sáng và các hiện tượng liên quan.

• 1. Giới Thiệu Về Giao Thoa 3 Ánh Sáng Đơn Sắc

  Giới thiệu khái quát về hiện tượng giao thoa ánh sáng, đặc biệt là khi sử dụng ba ánh sáng đơn sắc. Tìm hiểu về lịch sử và lý thuyết cơ bản.

• 2. Nguyên Lý Hoạt Động Của Giao Thoa Ánh Sáng

  Trình bày nguyên lý vật lý và các điều kiện cần thiết để tạo ra hiện tượng giao thoa của ba ánh sáng đơn sắc. Cung cấp các phương trình cơ bản và các yếu tố ảnh hưởng.

• 3. Các Thí Nghiệm Về Giao Thoa Ánh Sáng

  Miêu tả các thí nghiệm nổi bật trong việc nghiên cứu hiện tượng giao thoa ba ánh sáng đơn sắc. Cách tiến hành và các kết quả đáng chú ý.

• 4. Ứng Dụng Của Giao Thoa Ánh Sáng Trong Đời Sống

  Khám phá những ứng dụng thực tế của giao thoa ánh sáng trong các lĩnh vực như quang học, đo lường và công nghệ hiện đại.

• 5. Sự Khác Biệt Giữa Giao Thoa Hai Và Ba Ánh Sáng Đơn Sắc

  Phân tích sự khác biệt về mặt lý thuyết và thực tế giữa giao thoa hai ánh sáng đơn sắc và ba ánh sáng đơn sắc.

• 6. Tính Toán Các Hiện Tượng Giao Thoa

  Hướng dẫn cách tính toán các thông số của hiện tượng giao thoa ba ánh sáng đơn sắc như bước sóng, khoảng cách giữa các vân sáng tối.

• 7. Mô Phỏng Hiện Tượng Giao Thoa Bằng Phần Mềm

  Cách sử dụng phần mềm mô phỏng hiện tượng giao thoa ánh sáng để nghiên cứu và phân tích kết quả một cách chi tiết.

• 8. Các Câu Hỏi Thường Gặp Về Giao Thoa Ánh Sáng

  Danh sách các câu hỏi phổ biến liên quan đến giao thoa ba ánh sáng đơn sắc và câu trả lời chi tiết.

• 9. Những Sai Lầm Phổ Biến Khi Học Về Giao Thoa Ánh Sáng

  Những sai lầm thường gặp và cách tránh khi nghiên cứu về giao thoa ánh sáng, đặc biệt là với ba ánh sáng đơn sắc.

• 10. Tài Liệu Tham Khảo Và Đọc Thêm

  Tổng hợp các tài liệu, sách, và bài viết hữu ích để nghiên cứu sâu hơn về giao thoa ánh sáng đơn sắc.

Trong bài tập này, chúng ta sẽ tính toán vị trí của các vân sáng và vân tối khi ba nguồn ánh sáng đơn sắc giao thoa. Hãy giả định ba bước sóng khác nhau của ánh sáng là \(\lambda_1\), \(\lambda_2\) và \(\lambda_3\). Các bước thực hiện như sau:

1. Bước 1: Xác định bước sóng của từng ánh sáng đơn sắc.

   Giả sử, chúng ta có ba bước sóng lần lượt là \(\lambda_1 = 600 \, \text{nm}\), \(\lambda_2 = 500 \, \text{nm}\), và \(\lambda_3 = 400 \, \text{nm}\).

2. Bước 2: Tính toán khoảng cách giữa các vân sáng kế tiếp cho từng bước sóng.

   Công thức tính khoảng cách giữa các vân sáng là:

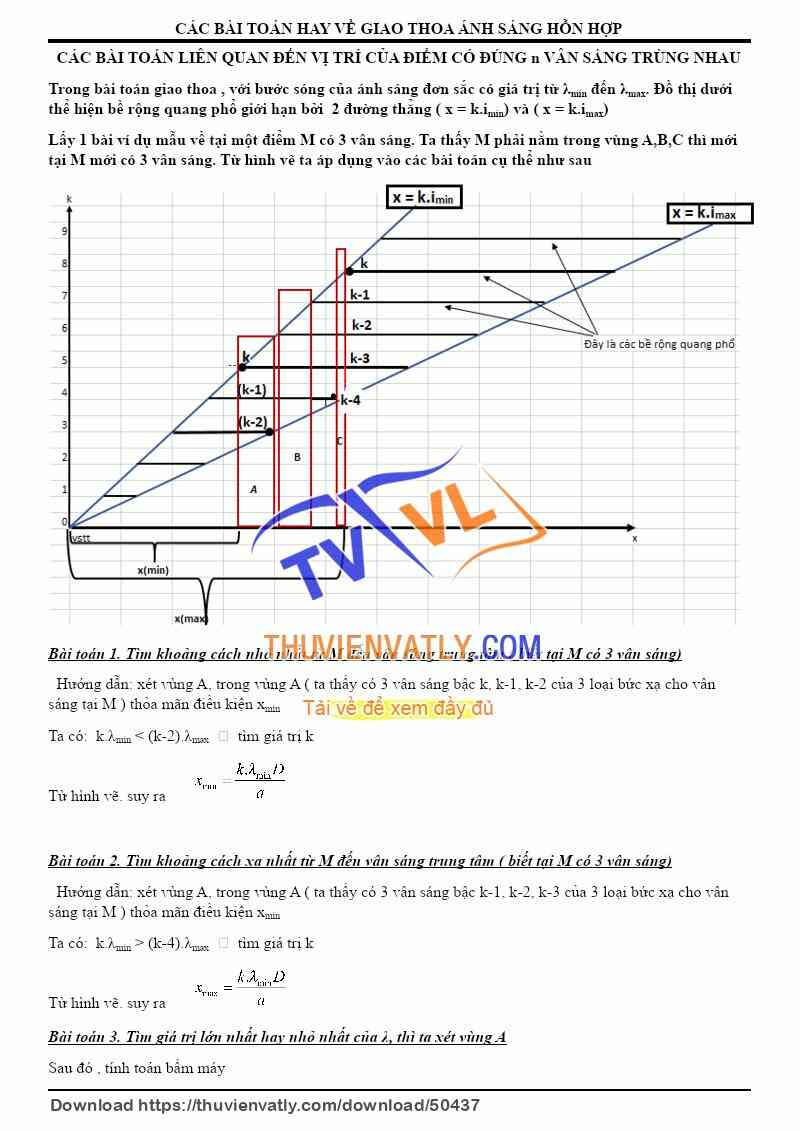
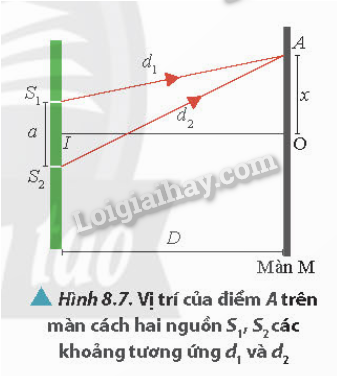
   \[ \Delta x = \frac{\lambda \cdot D}{a} \]

   Trong đó:

   • \(\lambda\) là bước sóng của ánh sáng.
   • \(D\) là khoảng cách từ hai khe sáng đến màn chắn.
   • \(a\) là khoảng cách giữa hai khe sáng.

3. Bước 3: Tính toán vị trí của các vân sáng.

   Vị trí của các vân sáng được xác định bởi công thức:

   \[ x = m \cdot \Delta x \]

   Với \(m\) là số nguyên, đại diện cho thứ tự của vân sáng (m = 0, ±1, ±2,...).

4. Bước 4: Xác định vị trí giao thoa giữa ba ánh sáng đơn sắc.

   Các vân sáng của ba ánh sáng sẽ giao thoa tại các vị trí mà:

   \[ x_1 = x_2 = x_3 \]

   Trong đó \(x_1\), \(x_2\), và \(x_3\) là vị trí các vân sáng tương ứng với từng bước sóng.

5. Bước 5: Xác định vị trí của vân tối giữa các vân sáng.

   Vân tối xuất hiện khi:

   \[ x = \left(m + \frac{1}{2}\right) \cdot \Delta x \]

   Trong đó, \(\Delta x\) là khoảng cách giữa các vân sáng của từng bước sóng.

Qua bài tập này, chúng ta có thể thấy rõ cách tính toán vị trí của các vân sáng và vân tối trong hiện tượng giao thoa ánh sáng của ba nguồn sáng đơn sắc khác nhau.

Trong dạng bài tập này, chúng ta sẽ khám phá cách giao thoa của ba ánh sáng đơn sắc có thể được ứng dụng trong phân tích quang phổ. Phương pháp này rất hữu ích trong việc phân tích thành phần và cấu trúc của các chất dựa trên quang phổ của chúng. Các bước thực hiện như sau:

1. Bước 1: Xác định các bước sóng của ba ánh sáng đơn sắc.

   Giả sử chúng ta có ba bước sóng khác nhau là \(\lambda_1\), \(\lambda_2\), và \(\lambda_3\). Các bước sóng này được lựa chọn sao cho phù hợp với dải quang phổ cần phân tích.

2. Bước 2: Thiết lập thí nghiệm giao thoa ánh sáng.

   Ba nguồn sáng đơn sắc được thiết lập để giao thoa trên một màn chắn. Màn chắn này sẽ hiển thị mô hình giao thoa dưới dạng các vân sáng và vân tối, từ đó phân tích các thành phần của quang phổ.

3. Bước 3: Phân tích mô hình giao thoa.

   Các vân giao thoa được hình thành tại những vị trí mà ba ánh sáng cùng pha và tạo ra sự tăng cường, trong khi vân tối xuất hiện khi các ánh sáng bị triệt tiêu lẫn nhau. Vị trí và độ rộng của các vân này có thể được sử dụng để xác định chính xác các bước sóng tham gia vào quang phổ.

4. Bước 4: So sánh kết quả với quang phổ mẫu.

   Các vị trí và cường độ của vân sáng trong mô hình giao thoa được so sánh với quang phổ mẫu để xác định thành phần và tính chất của chất cần phân tích.

5. Bước 5: Ứng dụng kết quả trong thực tiễn.

   Kết quả từ phân tích quang phổ bằng giao thoa ba ánh sáng đơn sắc có thể được áp dụng trong nhiều lĩnh vực, từ nghiên cứu khoa học đến sản xuất công nghiệp, giúp xác định thành phần hóa học và cấu trúc của vật liệu.

Dạng bài tập này không chỉ giúp hiểu rõ hơn về hiện tượng giao thoa ánh sáng mà còn mở ra các ứng dụng thực tiễn quan trọng trong phân tích quang phổ và nghiên cứu khoa học.

Trong dạng bài tập này, chúng ta sẽ giải quyết bài toán tìm khoảng cách giữa các vân sáng và vân tối trong hiện tượng giao thoa của ba ánh sáng đơn sắc. Đây là một bài toán phổ biến trong vật lý quang học, giúp hiểu rõ hơn về sự giao thoa và tính chất sóng của ánh sáng.

1. Bước 1: Xác định các bước sóng của ba ánh sáng đơn sắc.

   Giả sử ba ánh sáng có bước sóng lần lượt là \(\lambda_1\), \(\lambda_2\), và \(\lambda_3\). Các bước sóng này có thể được cho trước hoặc cần tính toán dựa trên dữ liệu thực nghiệm.

2. Bước 2: Thiết lập các điều kiện giao thoa.

   Giao thoa của ánh sáng xảy ra khi các sóng ánh sáng gặp nhau và tạo ra các vân giao thoa. Khoảng cách giữa các vân sáng hoặc vân tối được xác định bởi công thức:

   \[
   \Delta x = \frac{\lambda \cdot D}{a}
   \]
   Trong đó:
   

   
   
   • \(\Delta x\) là khoảng cách giữa hai vân sáng liên tiếp (hoặc hai vân tối liên tiếp).
   
   
   • \(\lambda\) là bước sóng của ánh sáng.
   
   
   • \(D\) là khoảng cách từ nguồn sáng đến màn quan sát.
   
   
   • \(a\) là khoảng cách giữa hai khe giao thoa.
   
   
   
   



3. Bước 3: Tính toán khoảng cách giữa các vân sáng tối.

   Để tính toán khoảng cách giữa các vân sáng tối, chúng ta sẽ áp dụng công thức đã nêu và thay thế các giá trị của \(\lambda\), \(D\), và \(a\) vào để tìm ra \(\Delta x\). Đối với mỗi ánh sáng đơn sắc, kết quả \(\Delta x\) sẽ khác nhau, tạo ra một mô hình giao thoa phức tạp hơn so với khi chỉ có hai ánh sáng đơn sắc.

4. Bước 4: So sánh và phân tích kết quả.

   Sau khi tính toán, chúng ta so sánh kết quả để xem khoảng cách giữa các vân sáng và tối có sự khác biệt như thế nào khi sử dụng ba ánh sáng đơn sắc khác nhau. Điều này giúp hiểu rõ hơn về ảnh hưởng của các yếu tố như bước sóng và khoảng cách giữa các khe giao thoa.

Dạng bài tập này giúp củng cố kiến thức về hiện tượng giao thoa ánh sáng và ứng dụng trong thực tế, đặc biệt là trong các thí nghiệm quang học và phân tích sóng ánh sáng.

Trong bài tập này, chúng ta sẽ phân tích sự ảnh hưởng của pha và bước sóng đến hiện tượng giao thoa của ánh sáng đơn sắc. Giao thoa ánh sáng xảy ra khi hai hay nhiều sóng ánh sáng kết hợp với nhau, tạo ra các vân sáng và tối trên màn ảnh. Đặc điểm của các vân này phụ thuộc vào sự khác biệt về pha và bước sóng của các sóng ánh sáng.

• 1. Ảnh hưởng của pha:

Giả sử hai nguồn sáng có cùng tần số và phát ra sóng ánh sáng đơn sắc nhưng có pha khác nhau. Khi sóng giao thoa, sự chênh lệch pha \(\Delta \phi\) sẽ quyết định vị trí của các vân sáng và tối. Cụ thể, các vân sáng xuất hiện khi sự chênh lệch pha giữa hai sóng là bội số chẵn của \(\pi\) (tức là \(\Delta \phi = 2k\pi\)), còn các vân tối xuất hiện khi chênh lệch pha là bội số lẻ của \(\pi\) (tức là \(\Delta \phi = (2k+1)\pi\)).

• 2. Ảnh hưởng của bước sóng:

Bước sóng \(\lambda\) cũng đóng vai trò quan trọng trong việc xác định khoảng cách giữa các vân. Khoảng cách giữa hai vân sáng liên tiếp (khoảng vân) được xác định theo công thức:

\[ i = \frac{\lambda D}{a} \]

Trong đó:

• \(i\) là khoảng cách giữa hai vân sáng liên tiếp.
• \(\lambda\) là bước sóng của ánh sáng sử dụng.
• \(D\) là khoảng cách từ khe tới màn.
• \(a\) là khoảng cách giữa hai khe sáng.

Khi bước sóng thay đổi, khoảng vân sẽ thay đổi theo, làm ảnh hưởng đến vị trí của các vân sáng và tối trên màn. Cụ thể, nếu bước sóng tăng, khoảng vân sẽ tăng và ngược lại.

• 3. Ứng dụng:

Hiểu rõ ảnh hưởng của pha và bước sóng đến giao thoa ánh sáng giúp ta giải quyết các bài toán thực tế liên quan đến việc xác định vị trí vân sáng/tối, từ đó có thể ứng dụng trong các lĩnh vực như đo lường khoảng cách, nghiên cứu vật liệu và thiết kế các thiết bị quang học.

Dạng bài tập này yêu cầu học sinh sử dụng phần mềm mô phỏng để thực hiện thí nghiệm giao thoa của ba ánh sáng đơn sắc với các bước sóng khác nhau. Đây là một cách tiếp cận thực tế và sinh động, giúp học sinh hiểu rõ hơn về các hiện tượng vật lý phức tạp trong giao thoa ánh sáng.

Các bước thực hiện mô phỏng:

1. Chuẩn bị phần mềm mô phỏng:

   Học sinh cần chuẩn bị một phần mềm mô phỏng giao thoa ánh sáng, chẳng hạn như PhET hoặc các công cụ trực tuyến tương tự. Những phần mềm này cho phép mô phỏng sự giao thoa của nhiều nguồn sáng khác nhau.

2. Cài đặt tham số:

   Trong phần mềm, cài đặt các tham số của ba ánh sáng đơn sắc có bước sóng lần lượt là \(\lambda_1 = 0,4 \, \mu m\), \(\lambda_2 = 0,5 \, \mu m\), và \(\lambda_3 = 0,6 \, \mu m\). Đặt khoảng cách giữa các khe là \(a = 2 \, mm\) và khoảng cách từ khe đến màn quan sát là \(D = 2 \, m\).

3. Thực hiện mô phỏng:

   Khởi chạy mô phỏng để quan sát các vân giao thoa được tạo ra bởi ba nguồn sáng. Học sinh cần chú ý đến các vân sáng và vân tối xuất hiện trên màn hình. Đặc biệt, tìm hiểu các vị trí trùng màu giữa ba nguồn sáng theo lý thuyết giao thoa ánh sáng.

4. Phân tích kết quả:

   Dựa trên kết quả mô phỏng, học sinh phân tích số lượng vân sáng, vân tối và các vị trí trùng nhau của ba ánh sáng đơn sắc. Ví dụ, vị trí trùng nhau gần nhất của ba bức xạ xảy ra khi \(k_1 = 15\), \(k_2 = 12\), và \(k_3 = 10\), nơi mà ba hệ vân giao thoa cùng một lúc.

5. Báo cáo kết quả:

   Cuối cùng, học sinh cần viết báo cáo mô tả quá trình thực hiện thí nghiệm, kết quả quan sát được, và so sánh với lý thuyết đã học. Báo cáo cần bao gồm hình ảnh minh họa từ phần mềm và nhận xét về sự trùng hợp của các vân sáng.

Trong bài toán này, chúng ta sẽ sử dụng hiện tượng giao thoa ánh sáng để đo lường bước sóng của các ánh sáng đơn sắc. Đây là một ứng dụng quan trọng trong các thí nghiệm quang học để xác định chính xác bước sóng của các nguồn sáng.

1. Đề bài

Một thí nghiệm giao thoa ánh sáng được thực hiện với ba ánh sáng đơn sắc có bước sóng lần lượt là \(\lambda_1\), \(\lambda_2\), và \(\lambda_3\). Các ánh sáng này tạo ra các vân giao thoa trên một màn quan sát cách các khe một khoảng \(D\). Biết khoảng cách giữa các khe là \(a\). Hãy tính bước sóng \(\lambda_1\) khi biết vị trí vân sáng bậc m của \(\lambda_1\) trùng với vị trí vân tối bậc n của \(\lambda_2\) và vân sáng bậc p của \(\lambda_3\).

2. Phương pháp giải

1. Xác định công thức cơ bản của vân sáng và vân tối trong hiện tượng giao thoa:

Vị trí vân sáng bậc m của ánh sáng có bước sóng \(\lambda_1\):

\[
x_m = \frac{m \lambda_1 D}{a}
\]

Vị trí vân tối bậc n của ánh sáng có bước sóng \(\lambda_2\):

\[
x_n = \frac{(n + 1/2) \lambda_2 D}{a}
\]

Vị trí vân sáng bậc p của ánh sáng có bước sóng \(\lambda_3\):

\[
x_p = \frac{p \lambda_3 D}{a}
\]

2. Thiết lập mối quan hệ giữa các vị trí vân sáng và vân tối:

Vì vân sáng bậc m của \(\lambda_1\) trùng với vân tối bậc n của \(\lambda_2\), ta có:

\[
\frac{m \lambda_1 D}{a} = \frac{(n + 1/2) \lambda_2 D}{a}
\]

Và đồng thời cũng trùng với vân sáng bậc p của \(\lambda_3\):

\[
\frac{m \lambda_1 D}{a} = \frac{p \lambda_3 D}{a}
\]

3. Giải hệ phương trình để tìm \(\lambda_1\):

Từ hai phương trình trên, ta rút ra được:

\[
\lambda_1 = \frac{(n + 1/2) \lambda_2}{m}
\]

\[
\lambda_1 = \frac{p \lambda_3}{m}
\]

Cuối cùng, kết hợp các kết quả để tính toán giá trị cụ thể của \(\lambda_1\).

3. Ví dụ cụ thể

Giả sử trong thí nghiệm, ánh sáng thứ hai có bước sóng \(\lambda_2 = 600 nm\), ánh sáng thứ ba có bước sóng \(\lambda_3 = 500 nm\), và các thông số khác như sau:

• Vân sáng bậc m = 3
• Vân tối bậc n = 2
• Vân sáng bậc p = 4

Áp dụng công thức:

\[
\lambda_1 = \frac{(2 + 1/2) \times 600 nm}{3} = 500 nm
\]

Vậy, bước sóng \(\lambda_1\) của ánh sáng thứ nhất là 500 nm, trùng khớp với bước sóng của ánh sáng thứ ba trong ví dụ này.

Trong thí nghiệm về sự giao thoa ánh sáng, khi ánh sáng đi qua các môi trường khác nhau, các đặc tính của sóng ánh sáng như bước sóng, tốc độ và góc lệch sẽ thay đổi. Điều này làm ảnh hưởng đến hiện tượng giao thoa và vân sáng - vân tối trên màn quan sát.

Ví dụ, khi ánh sáng đi từ không khí vào nước, bước sóng của ánh sáng giảm, do đó khoảng cách giữa các vân giao thoa cũng giảm. Để giải quyết các bài tập liên quan đến sự giao thoa trong môi trường khác nhau, ta cần thực hiện theo các bước sau:

1. Bước 1: Xác định các thông số cơ bản của thí nghiệm như bước sóng \( \lambda \), khoảng cách giữa hai khe \( a \), và khoảng cách từ hai khe đến màn \( D \).

2. Bước 2: Xác định môi trường mới mà ánh sáng đi qua và tính toán lại bước sóng trong môi trường đó bằng công thức:

   \[ \lambda' = \frac{\lambda}{n} \]

   Trong đó \( n \) là chiết suất của môi trường mới.

3. Bước 3: Tính khoảng cách giữa các vân giao thoa trong môi trường mới:

   \[ i' = \frac{\lambda' D}{a} \]

   Đây là khoảng cách giữa hai vân sáng liên tiếp trên màn.

4. Bước 4: Áp dụng các công thức đã biết để tính toán số lượng vân sáng hoặc khoảng cách giữa các vân khi có sự thay đổi môi trường.

Dưới đây là một ví dụ cụ thể:

Trong một thí nghiệm Y-âng với ánh sáng đơn sắc, nếu ánh sáng ban đầu có bước sóng \( \lambda = 0,6 \mu m \) và khi đi qua một môi trường có chiết suất \( n = 1,5 \), ta có bước sóng mới là:

\[ \lambda' = \frac{0,6 \mu m}{1,5} = 0,4 \mu m \]

Giả sử khoảng cách giữa hai khe là \( a = 1 mm \) và khoảng cách từ hai khe đến màn là \( D = 2 m \), khoảng cách giữa các vân sáng mới sẽ là:

\[ i' = \frac{0,4 \times 10^{-6} \times 2}{1 \times 10^{-3}} = 0,8 mm \]

Qua ví dụ này, chúng ta thấy rõ sự thay đổi môi trường dẫn đến sự thay đổi khoảng cách giữa các vân giao thoa. Điều này rất quan trọng trong việc giải các bài tập liên quan đến giao thoa ánh sáng trong môi trường khác nhau.

Trong hiện tượng giao thoa ánh sáng với ba nguồn sáng đơn sắc có bước sóng khác nhau, cường độ ánh sáng tổng hợp tại một điểm trên màn sẽ được tính toán dựa vào cường độ của từng ánh sáng thành phần.

1. Xét ba nguồn sáng đơn sắc có cường độ lần lượt là \(I_1\), \(I_2\), và \(I_3\) với các bước sóng tương ứng là \(\lambda_1\), \(\lambda_2\), và \(\lambda_3\).

2. Giả sử các nguồn sáng này có cùng pha ban đầu tại điểm phát, tại một điểm trên màn, cường độ tổng hợp \(I\) được tính theo công thức:

   \[
   I = I_1 + I_2 + I_3 + 2\sqrt{I_1 I_2} \cos \varphi_{12} + 2\sqrt{I_2 I_3} \cos \varphi_{23} + 2\sqrt{I_3 I_1} \cos \varphi_{31}
   \]

3. Trong đó, \(\varphi_{12}\), \(\varphi_{23}\), \(\varphi_{31}\) lần lượt là hiệu số pha giữa hai sóng tương ứng.

4. Hiệu số pha có thể tính bằng công thức:

   \[
   \varphi_{ij} = \dfrac{2\pi d_{ij}}{\lambda_{ij}} + \varphi_{ij0}
   \]

   Với \(d_{ij}\) là hiệu quang lộ giữa hai sóng đến từ hai nguồn \(i\) và \(j\), \(\lambda_{ij}\) là bước sóng của sóng tổng hợp giữa hai nguồn, và \(\varphi_{ij0}\) là pha ban đầu.

5. Sau khi tính được các hiệu số pha, ta thay vào công thức tổng hợp cường độ để tìm cường độ sáng tổng hợp tại điểm đang xét.

6. Cuối cùng, giá trị cường độ sáng tổng hợp sẽ quyết định mức độ sáng hoặc tối của điểm trên màn giao thoa.

Trong hiện tượng giao thoa ánh sáng, các yếu tố như bước sóng của ánh sáng, khoảng cách giữa hai khe, và khoảng cách từ các khe đến màn ảnh đều có ảnh hưởng lớn đến kết quả giao thoa. Dưới đây là cách khảo sát hiện tượng giao thoa khi các yếu tố này thay đổi.

1. Thay đổi bước sóng của ánh sáng:

   • Khi bước sóng ánh sáng \(\lambda\) tăng, khoảng vân giao thoa \(\Delta x\) cũng tăng theo, do đó các vân sáng và vân tối trên màn sẽ thưa hơn.
   • Khi bước sóng giảm, khoảng vân \(\Delta x\) giảm, các vân sáng và tối sẽ gần nhau hơn.
   • Khoảng vân \(\Delta x\) được xác định bằng công thức:

   \[\Delta x = \dfrac{\lambda D}{a}\]

   • Trong đó:
   • \(\lambda\) là bước sóng của ánh sáng.
   • D là khoảng cách từ khe đến màn.
   • a là khoảng cách giữa hai khe.

2. Thay đổi khoảng cách giữa hai khe:

   • Nếu khoảng cách giữa hai khe \(a\) tăng, khoảng vân \(\Delta x\) sẽ giảm, do đó các vân sáng và tối sẽ gần nhau hơn.
   • Nếu khoảng cách giữa hai khe \(a\) giảm, khoảng vân \(\Delta x\) sẽ tăng, các vân sáng và tối sẽ thưa hơn.
   • Công thức liên quan vẫn là:

   \[\Delta x = \dfrac{\lambda D}{a}\]

3. Thay đổi khoảng cách từ các khe đến màn:

   • Khi khoảng cách từ các khe đến màn \(D\) tăng, khoảng vân \(\Delta x\) sẽ tăng theo, do đó các vân sáng và tối sẽ thưa hơn.
   • Khi khoảng cách từ các khe đến màn \(D\) giảm, khoảng vân \(\Delta x\) sẽ giảm, các vân sáng và tối sẽ gần nhau hơn.
   • Công thức liên quan:

   \[\Delta x = \dfrac{\lambda D}{a}\]

4. Ví dụ minh họa:

   Giả sử có ba nguồn sáng đơn sắc với các bước sóng khác nhau \(\lambda_1\), \(\lambda_2\), và \(\lambda_3\). Nếu thay đổi lần lượt các yếu tố như bước sóng, khoảng cách giữa hai khe, và khoảng cách từ khe đến màn, ta sẽ thu được các kết quả giao thoa khác nhau:

   • Với bước sóng \(\lambda_1\): khoảng vân giao thoa là \(\Delta x_1\).
   • Với bước sóng \(\lambda_2\): khoảng vân giao thoa là \(\Delta x_2\).
   • Với bước sóng \(\lambda_3\): khoảng vân giao thoa là \(\Delta x_3\).

   Những sự thay đổi này giúp chúng ta hiểu rõ hơn về mối liên hệ giữa các yếu tố tham gia và hiện tượng giao thoa ánh sáng.

Dạng bài tập này tập trung vào việc phân tích và giải quyết các tình huống giao thoa của ba ánh sáng đơn sắc khác nhau. Những bài tập này thường yêu cầu học sinh phải tính toán số lượng vân sáng, vân tối, vị trí các vân, và các đặc điểm của hình ảnh giao thoa thu được trên màn.

• Giả sử ba ánh sáng đơn sắc có bước sóng \(\lambda_1\), \(\lambda_2\), và \(\lambda_3\).
• Các bước sóng này sẽ tạo ra các hệ vân giao thoa riêng biệt trên màn với các khoảng vân tương ứng \(i_1\), \(i_2\), \(i_3\).

Bài tập tổng hợp thường yêu cầu thực hiện các bước sau:

1. Xác định các khoảng vân \(i_1\), \(i_2\), và \(i_3\) dựa trên các bước sóng \(\lambda_1\), \(\lambda_2\), và \(\lambda_3\), cùng với các thông số thực nghiệm như khoảng cách giữa hai khe và khoảng cách từ khe đến màn.
2. Tính toán vị trí các vân sáng trùng nhau của ba ánh sáng này trên màn. Vị trí này thường là nghiệm của phương trình:
\[ \frac{{k_1}}{{i_1}} = \frac{{k_2}}{{i_2}} = \frac{{k_3}}{{i_3}} \]
3. Xác định số lượng vân sáng và vân tối xuất hiện trong khoảng giao thoa xác định, và đếm số vân sáng có màu sắc giống với vân sáng trung tâm.
4. Giải các bài toán yêu cầu xác định vị trí và số lượng vân sáng cùng màu, như ví dụ tính toán vị trí trùng nhau của ba vân sáng bậc \(k_1\), \(k_2\), và \(k_3\).

Ví dụ thực tế:

• Trong thí nghiệm Y-âng về giao thoa ánh sáng, với ánh sáng có ba bức xạ đơn sắc \(\lambda_1 = 0,4 \, \mu m\), \(\lambda_2 = 0,56 \, \mu m\), và \(\lambda_3 = 0,6 \, \mu m\), các vân sáng trùng nhau được xác định dựa trên tỷ lệ bước sóng và khoảng vân tương ứng.
• Kết quả là ta có thể xác định số lượng và vị trí các vân sáng trùng nhau và tính toán độ rộng miền giao thoa trên màn.

Việc nắm vững dạng bài tập này giúp học sinh có thể vận dụng linh hoạt các công thức và phương pháp để giải quyết những bài toán phức tạp về giao thoa ánh sáng trong thực tế.