Chủ đề chuyển động thẳng biến đổi đều vật lý 10: Chuyển động thẳng biến đổi đều là một phần quan trọng trong Vật lý lớp 10. Bài viết này cung cấp kiến thức chi tiết về khái niệm, công thức, và các bài tập liên quan, giúp học sinh nắm vững nội dung và dễ dàng áp dụng vào thực tiễn. Hãy cùng khám phá và giải quyết những bài toán thú vị!
Mục lục
Chuyển động thẳng biến đổi đều - Vật lý lớp 10
Chuyển động thẳng biến đổi đều là một trong những nội dung quan trọng trong chương trình Vật lý lớp 10, giúp học sinh hiểu về các quy luật chuyển động và các đại lượng liên quan. Dưới đây là các khái niệm cơ bản, công thức và ví dụ minh họa chi tiết.
1. Định nghĩa
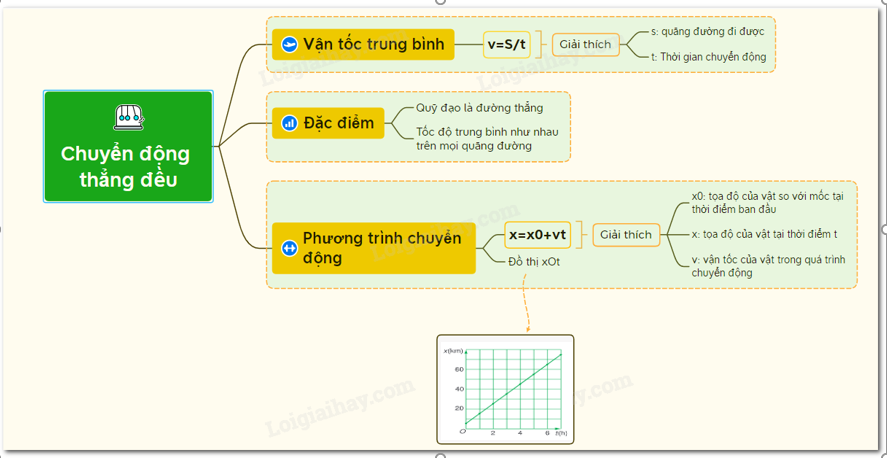
Chuyển động thẳng biến đổi đều là chuyển động có quỹ đạo là một đường thẳng, trong đó độ lớn của vận tốc tức thời tăng đều hoặc giảm đều theo thời gian.
- Chuyển động nhanh dần đều: Vận tốc tăng đều theo thời gian.
- Chuyển động chậm dần đều: Vận tốc giảm đều theo thời gian.
2. Các đại lượng trong chuyển động thẳng biến đổi đều
Trong chuyển động thẳng biến đổi đều, các đại lượng cơ bản bao gồm:
- Gia tốc (a): Đặc trưng cho độ biến thiên của vận tốc theo thời gian, được tính bằng công thức: \[ a = \frac{{v - v_0}}{{t - t_0}} \]
- Phương trình vận tốc: Liên hệ giữa vận tốc, gia tốc và thời gian: \[ v = v_0 + a(t - t_0) \]
- Phương trình tọa độ: Liên hệ giữa tọa độ, vận tốc và gia tốc: \[ x = x_0 + v_0(t - t_0) + \frac{1}{2}a(t - t_0)^2 \]
- Hệ thức độc lập thời gian: Công thức liên hệ giữa vận tốc và quãng đường mà không cần biết thời gian: \[ v^2 - v_0^2 = 2a\Delta x \]
3. Đồ thị chuyển động thẳng biến đổi đều
Các đồ thị quan trọng trong chuyển động thẳng biến đổi đều bao gồm:
- Đồ thị vận tốc - thời gian (v-t): Là một đường thẳng xiên, biểu diễn sự biến thiên của vận tốc theo thời gian. Diện tích dưới đường v-t cho biết quãng đường mà vật đi được.
- Đồ thị gia tốc - thời gian (a-t): Là một đường thẳng song song với trục thời gian, biểu diễn gia tốc không đổi.
- Đồ thị tọa độ - thời gian (x-t): Là một phần của đường parabol, biểu diễn sự thay đổi tọa độ theo thời gian.
4. Ví dụ minh họa
Chất điểm chuyển động thẳng nhanh dần đều với vận tốc ban đầu là \(v_0 = 2 \, m/s\), gia tốc \(a = 1 \, m/s^2\). Tính vận tốc và quãng đường đi được sau 5 giây.
- Vận tốc: Áp dụng phương trình vận tốc: \[ v = v_0 + at = 2 + 1 \cdot 5 = 7 \, m/s \]
- Quãng đường: Áp dụng phương trình tọa độ: \[ s = v_0t + \frac{1}{2}at^2 = 2 \cdot 5 + \frac{1}{2} \cdot 1 \cdot 5^2 = 10 + 12.5 = 22.5 \, m \]
5. Bài tập vận dụng
Dưới đây là một số bài tập vận dụng giúp học sinh củng cố kiến thức về chuyển động thẳng biến đổi đều:
- Một ô tô chuyển động thẳng nhanh dần đều với gia tốc \(a = 2 \, m/s^2\). Biết vận tốc ban đầu là \(v_0 = 5 \, m/s\). Tính vận tốc của ô tô sau 4 giây.
- Một vật chuyển động thẳng chậm dần đều với vận tốc ban đầu \(v_0 = 10 \, m/s\) và gia tốc \(a = -2 \, m/s^2\). Tính quãng đường mà vật đi được trong 6 giây.
6. Kết luận
Chuyển động thẳng biến đổi đều là một khái niệm cơ bản trong Vật lý, giúp chúng ta hiểu rõ hơn về các quy luật chuyển động và ứng dụng trong nhiều bài toán thực tế. Việc nắm vững kiến thức này sẽ giúp học sinh phát triển kỹ năng giải bài tập và áp dụng vào thực tiễn.

.png)
1. Khái niệm về chuyển động thẳng biến đổi đều
Chuyển động thẳng biến đổi đều là loại chuyển động trong đó vận tốc của vật thay đổi đều theo thời gian. Điều này có nghĩa là độ lớn vận tốc của vật có thể tăng hoặc giảm đều theo thời gian, và gia tốc của chuyển động luôn không đổi. Tùy thuộc vào sự thay đổi của vận tốc, chuyển động thẳng biến đổi đều có thể được chia thành hai loại: chuyển động nhanh dần đều và chuyển động chậm dần đều.
- Chuyển động nhanh dần đều: là chuyển động mà vận tốc của vật tăng đều theo thời gian. Trong trường hợp này, gia tốc có cùng hướng với vận tốc ban đầu.
- Chuyển động chậm dần đều: là chuyển động mà vận tốc của vật giảm đều theo thời gian. Trong trường hợp này, gia tốc ngược hướng với vận tốc ban đầu.
Công thức liên quan
- Vận tốc tức thời: \[ v = v_0 + a t \] với \( v_0 \) là vận tốc ban đầu, \( a \) là gia tốc, và \( t \) là thời gian.
- Quãng đường đi được: \[ S = v_0 t + \frac{1}{2} a t^2 \] Đây là công thức tính quãng đường mà vật đi được trong chuyển động thẳng biến đổi đều.
- Phương trình chuyển động: \[ x = x_0 + v_0 t + \frac{1}{2} a t^2 \] với \( x_0 \) là vị trí ban đầu của vật.
- Công thức liên hệ giữa vận tốc, gia tốc và quãng đường: \[ v^2 - v_0^2 = 2 a S \] Đây là công thức không chứa thời gian, sử dụng để tính vận tốc cuối khi biết gia tốc và quãng đường đi được.
Các công thức trên là cơ sở quan trọng để phân tích các bài toán liên quan đến chuyển động thẳng biến đổi đều trong chương trình Vật lý lớp 10. Việc nắm vững các khái niệm và công thức này giúp học sinh giải quyết tốt các bài toán liên quan.
2. Các đại lượng đặc trưng trong chuyển động thẳng biến đổi đều
Trong chuyển động thẳng biến đổi đều, có nhiều đại lượng vật lý quan trọng cần chú ý để hiểu rõ bản chất của quá trình chuyển động. Dưới đây là các đại lượng chính được sử dụng để mô tả loại chuyển động này:
- Gia tốc:
Gia tốc \( a \) là đại lượng đặc trưng cho sự thay đổi của vận tốc trong quá trình chuyển động. Nó được xác định bằng công thức:
\[ a = \frac{\Delta v}{\Delta t} \]- Với \( \Delta v \) là độ biến thiên vận tốc.
- Đơn vị của gia tốc là m/s2.
- Gia tốc là không đổi trong chuyển động thẳng biến đổi đều, có thể là dương (chuyển động nhanh dần đều) hoặc âm (chuyển động chậm dần đều).
- Vận tốc:
Vận tốc \( v \) tại thời điểm bất kỳ trong chuyển động thẳng biến đổi đều được tính theo công thức:
\[ v = v_0 + a.t \]- Trong đó \( v_0 \) là vận tốc ban đầu, \( t \) là thời gian.
- Vận tốc là hàm bậc nhất của thời gian, có thể dương hoặc âm tùy theo hướng chuyển động.
- Quãng đường:
Quãng đường \( S \) vật đi được trong chuyển động thẳng biến đổi đều được tính bằng công thức:
\[ S = v_0.t + \frac{1}{2}a.t^2 \]- Quãng đường phụ thuộc vào vận tốc ban đầu, gia tốc và thời gian chuyển động.
- Phương trình chuyển động:
Phương trình tổng quát của chuyển động thẳng biến đổi đều là:
\[ x = x_0 + v_0.t + \frac{1}{2}a.t^2 \]- \( x \) là vị trí của vật tại thời điểm \( t \), và \( x_0 \) là vị trí ban đầu.
- Công thức liên hệ giữa vận tốc, gia tốc và quãng đường:
Công thức liên hệ giữa vận tốc, gia tốc và quãng đường (không phụ thuộc vào thời gian) là:
\[ v^2 - v_0^2 = 2aS \]- Công thức này cho phép tính quãng đường mà không cần biết thời gian chuyển động.

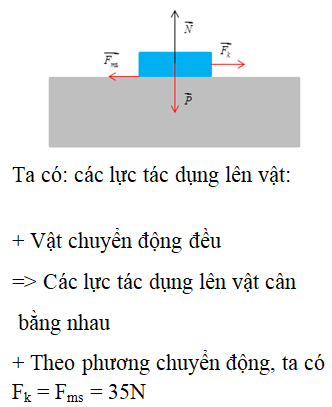
4. Bài tập áp dụng về chuyển động thẳng biến đổi đều

5. Ứng dụng thực tế của chuyển động thẳng biến đổi đều
Chuyển động thẳng biến đổi đều có nhiều ứng dụng thực tế trong đời sống và kỹ thuật. Những ứng dụng này giúp chúng ta hiểu rõ hơn về các hiện tượng và quá trình diễn ra xung quanh, đồng thời hỗ trợ việc cải tiến công nghệ và phát triển các lĩnh vực khác nhau. Dưới đây là một số ví dụ minh họa về ứng dụng của chuyển động thẳng biến đổi đều:
5.1. Ví dụ trong giao thông
-
Phanh xe ô tô: Khi ô tô phanh gấp, chuyển động của xe là một ví dụ điển hình của chuyển động chậm dần đều. Vận tốc của xe giảm dần với một gia tốc âm và quá trình này diễn ra đều đặn cho đến khi xe dừng hẳn. Việc tính toán chính xác gia tốc và thời gian phanh là rất quan trọng để đảm bảo an toàn giao thông.
-
Gia tốc của xe khi tăng tốc: Khi ô tô bắt đầu di chuyển từ trạng thái đứng yên, nó trải qua quá trình tăng tốc đều (chuyển động nhanh dần đều). Gia tốc không đổi giúp xe đạt được vận tốc mong muốn sau một khoảng thời gian nhất định. Đây là cơ sở cho việc tối ưu hóa tiết kiệm nhiên liệu và cải thiện hiệu suất động cơ.
5.2. Ví dụ trong công nghệ sản xuất
-
Dây chuyền sản xuất tự động: Trong các nhà máy hiện đại, chuyển động thẳng biến đổi đều được áp dụng để điều khiển tốc độ di chuyển của băng chuyền hoặc các thiết bị robot. Khi khởi động hoặc dừng lại, chúng thường di chuyển với gia tốc không đổi để tránh các va chạm hoặc gián đoạn trong quá trình sản xuất.
-
Quá trình gia công cơ khí: Trong các máy tiện hoặc máy CNC, khi cần gia công chi tiết, dao cắt thường di chuyển theo quỹ đạo thẳng với tốc độ không đổi hoặc có gia tốc nhất định để đảm bảo chất lượng sản phẩm và độ chính xác cao.

6. Một số lưu ý khi học và làm bài tập
Khi học và làm bài tập về chuyển động thẳng biến đổi đều, học sinh cần lưu ý một số điểm quan trọng để hiểu rõ bản chất và giải bài hiệu quả. Dưới đây là những lưu ý cần thiết:
- 1. Phân biệt rõ các loại chuyển động:
Chuyển động thẳng biến đổi đều có hai loại chính là chuyển động nhanh dần đều và chuyển động chậm dần đều.
Hãy nắm vững sự khác biệt giữa hai loại này: chuyển động nhanh dần đều có vận tốc tăng dần theo thời gian, trong khi chuyển động chậm dần đều có vận tốc giảm dần. Điều này giúp tránh nhầm lẫn khi làm bài tập. - 2. Hiểu các công thức cơ bản:
Các công thức quan trọng như phương trình vận tốc \(v = v_0 + at\), phương trình tọa độ \(x = x_0 + v_0t + \frac{1}{2}at^2\), và hệ thức độc lập thời gian \(v^2 - v_0^2 = 2a(x - x_0)\) là nền tảng để giải các bài toán chuyển động thẳng biến đổi đều. Hãy hiểu rõ ý nghĩa của từng đại lượng trong các công thức này.
- 3. Vẽ và phân tích đồ thị:
Đồ thị vận tốc – thời gian và tọa độ – thời gian là công cụ mạnh mẽ giúp phân tích chuyển động. Đặc biệt, đồ thị vận tốc – thời gian có dạng đường thẳng, và gia tốc chính là độ dốc của đồ thị này. Hãy tập vẽ và phân tích các dạng đồ thị để hiểu rõ cách biến đổi của vận tốc và gia tốc theo thời gian.
- 4. Thực hành bài tập thường xuyên:
Làm nhiều dạng bài tập khác nhau từ đơn giản đến phức tạp là cách tốt nhất để củng cố kiến thức. Bạn nên bắt đầu với các bài tập cơ bản để hiểu cách áp dụng công thức, sau đó thử thách bản thân với các bài toán có đồ thị hoặc bài toán yêu cầu tính gia tốc, vận tốc trung bình.
- 5. Sử dụng đơn vị nhất quán:
Luôn chú ý đến đơn vị của các đại lượng vật lý trong bài toán. Vận tốc thường tính bằng m/s, gia tốc là m/s², và thời gian là giây. Việc không đồng nhất đơn vị có thể dẫn đến kết quả sai.
- 6. Kiểm tra kết quả:
Sau khi giải xong bài tập, hãy kiểm tra lại kết quả bằng cách xem xét các yếu tố hợp lý như: vận tốc và gia tốc có cùng dấu trong chuyển động nhanh dần đều, hay khác dấu trong chuyển động chậm dần đều. Điều này giúp xác nhận bài giải đã đúng.