Học tốt hình học không gian với bản đồ tư duy

Để giải một bài toán hình học không gian thành công, lưu ý rằng cần có một số bước cần thiết. Đầu tiên, hãy đọc đề bài cẩn thận và phân tích giả thuyết của bài toán. Tiếp theo, hãy vẽ hình đúng, đặc biệt cần xác định các yếu tố khác như điểm phụ, đường phụ, mặt phẳng phụ (nếu cần) để giúp cho quá trình giải toán.

Theo cô Hà Thị Thu Hồng, trong hình học không gian, có năm bài toán lớn cần chú ý. Bài toán thứ nhất là “Tìm tương giao”, bao gồm việc tìm giao điểm của hai đường thẳng, giao điểm của đường với mặt và giao tuyến của hai mặt phẳng. Bài toán thứ hai là “Quan hệ song song”, bao gồm chứng minh và dựng hình liên quan đến hai đường thẳng song song, đường thẳng song song với mặt phẳng và hai mặt phẳng song song. Bài toán thứ ba là “Quan hệ vuông góc”, bao gồm chứng minh và dựng hình liên quan đến hai đường thẳng vuông góc, đường thẳng vuông góc với mặt phẳng và hai mặt phẳng vuông góc. Bài toán thứ tư là “Bài toán về góc”, bao gồm xác định và tính góc giữa hai đường thẳng, góc giữa đường thẳng và mặt phẳng, góc giữa hai mặt phẳng. Bài toán thứ năm là “Bài toán về khoảng cách”, bao gồm xác định và tính khoảng cách từ một điểm đến một đường thẳng, một mặt phẳng, giữa hai đường thẳng song song, hai mặt phẳng song song và hai đường thẳng chéo nhau.

Bạn đang xem: Học tốt hình học không gian với bản đồ tư duy

Mỗi bài toán lớn này tập trung vào các bài toán nhỏ khác nhau, và chúng không nằm ở cùng một chương hoặc một bài. Để dạy tốt và học tốt, cô Hồng cho rằng giáo viên cần hướng dẫn học sinh nắm vững các nội dung trọng tâm nhất và bài toán quan trọng nhất để từ đó có thể giải quyết các bài toán nhỏ khác.

Xem thêm : Nguyên nhân khiến trẻ thiếu tập trung khi học

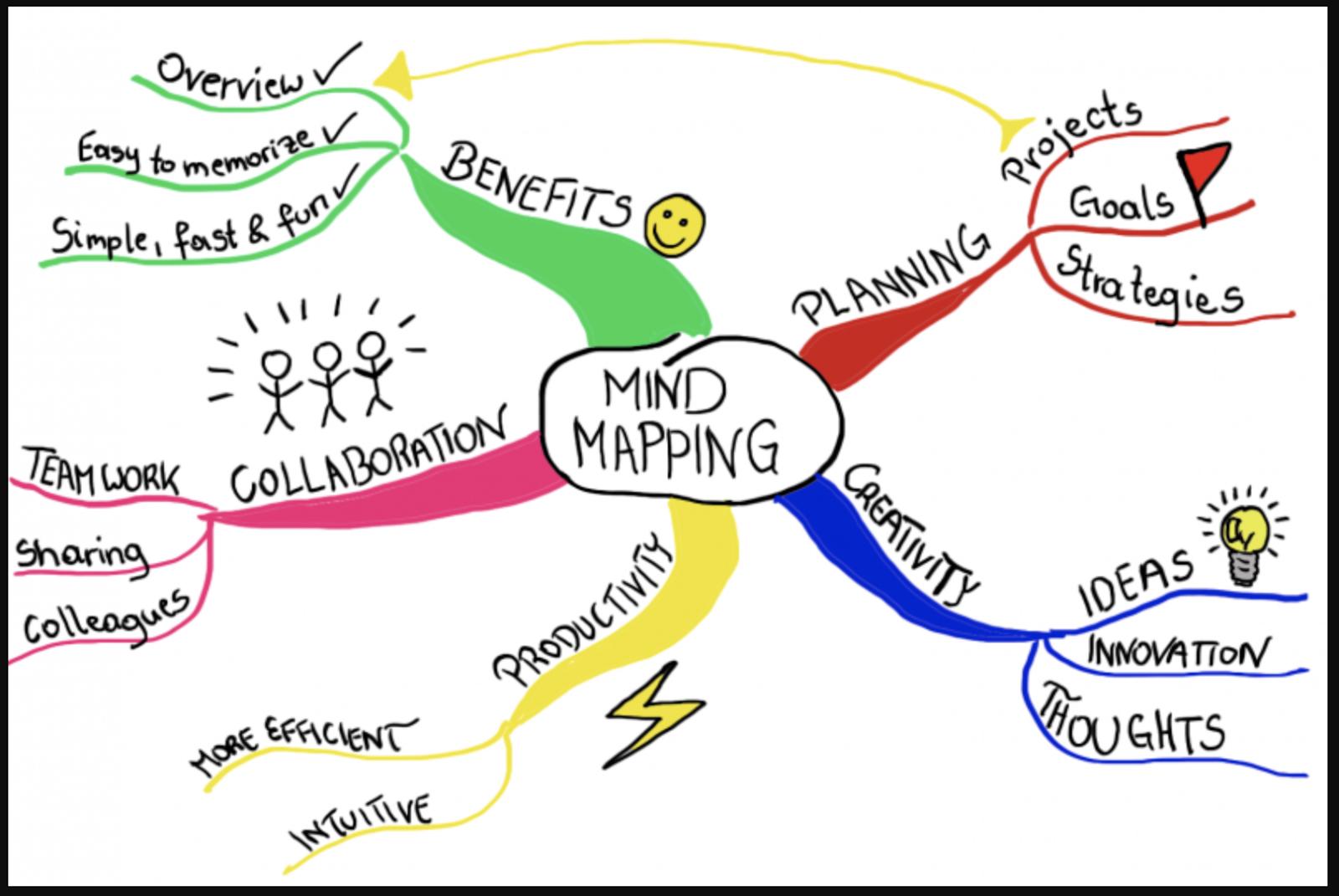
Thêm vào đó, sử dụng bản đồ tư duy là một phương pháp hiệu quả để hệ thống hóa lí thuyết và giúp học sinh dễ hiểu và dễ nhớ. Giáo viên có thể sử dụng bản đồ tư duy trong việc giảng dạy và giải toán.

Ví dụ, trong bài toán tìm tương giao, việc tìm giao điểm của hai đường thẳng, giao điểm của đường với mặt phẳng và giao tuyến của hai mặt phẳng là quan trọng nhất. Cách dễ nhất để chứng minh tương giao là tìm giao điểm của hai đường thẳng này.

Đối với bài toán “Quan hệ song song”, chú trọng vào việc chứng minh và dựa vào quan hệ song song để dựng hình. Chứng minh hai đường thẳng song song là quan trọng nhất, và các bài toán chứng minh khác có thể được đưa về bài toán này.

Xem thêm : Câu nói ‘Trẻ lên ba cả nhà học nói’ và lời nhắc nhở dành cho mỗi bậc phụ huynh

Bài toán “Quan hệ vuông góc” tập trung vào việc chứng minh các quan hệ vuông góc. Chứng minh hai đường thẳng vuông góc là quan trọng nhất, và các bài toán khác có thể được giải quyết dựa trên bài toán này.

Trường hợp của bài toán về góc bao gồm việc xác định và tính toán góc giữa các đường thẳng và mặt phẳng. Việc xác định và tính toán góc giữa hai đường thẳng là quan trọng nhất, và các bài toán khác có thể được đưa về bài toán này.

Cuối cùng, trong bài toán về khoảng cách, việc tính toán khoảng cách từ một điểm đến đường thẳng là quan trọng nhất. Các bài toán tính khoảng cách khác có thể được giải quyết dựa trên bài toán này.

Với bản đồ tư duy, có thể hệ thống hóa lí thuyết và giúp học sinh dễ hiểu và nhớ lâu hơn. Hãy áp dụng cách này trong việc giảng dạy và giải toán hình học không gian để đạt được kết quả tốt nhất.

Nguồn: https://ispacedanang.edu.vn
Danh mục: Học tư duy