Đạo Hàm Căn x: Khái Niệm, Công Thức và Ứng Dụng Thực Tế

Đạo hàm của hàm số căn x là một trong những công thức cơ bản và quan trọng trong giải tích. Dưới đây là hướng dẫn chi tiết về cách tính đạo hàm của căn x và các biến thể khác nhau của nó.

Công Thức Tổng Quát

Đạo hàm của hàm số (y = căn x) được tính theo công thức:

Bạn đang xem: Đạo Hàm Căn x: Khái Niệm, Công Thức và Ứng Dụng Thực Tế

d/dx (căn x) = 1 / (2 * căn x)

Các Biến Thể Khác

Xem thêm : Trường Cao đẳng nghề Du lịch Sài Gòn đào tạo ngành gì? Điều kiện xét tuyển

Đối với đạo hàm của hàm số có dạng (y = căn u(x)), ta sử dụng quy tắc chuỗi để tính:

d/dx (căn u(x)) = u'(x) / (2 * căn u(x))

Công Thức Đạo Hàm Căn Bậc n

Để tính đạo hàm của hàm số dạng (y = (căn x)^n), ta áp dụng công thức:

d/dx ((căn x)^n) = (n/2) * x^((n/2) - 1)

Ví Dụ Minh Họa

Ví Dụ 1: Tính Đạo Hàm của (y = căn(x^2 + 1))

1. Gọi (u = x^2 + 1)
2. Đạo hàm của (u) là (u’ = 2x)
3. Áp dụng công thức đạo hàm căn, ta có:

d/dx (căn(x^2 + 1)) = (2x) / (2 * căn(x^2 + 1)) = x / căn(x^2 + 1)

Ví Dụ 2: Tính Đạo Hàm của (y = x * căn(x))

1. Sử dụng quy tắc tích, ta có:

d/dx (x * căn(x)) = x * d/dx (căn(x)) + căn(x) * d/dx (x)

2. Thay giá trị đạo hàm, ta được:

= x * (1 / (2 * căn(x))) + căn(x) * 1 = (x / (2 * căn(x))) + căn(x) = (x + 2x) / (2 * căn(x)) = (3x) / (2 * căn(x))

Ứng Dụng

Xem thêm : Một Phó Giám đốc Sở Khoa học và Công nghệ TP. Hồ Chí Minh xin thôi việc

Đạo hàm của căn x và các dạng biến thể của nó được áp dụng nhiều trong các bài toán tìm cực trị, nghiên cứu sự biến thiên của hàm số, và giải quyết các bài toán vật lý và kỹ thuật.

Bài Tập Vận Dụng

Bài Tập 1: Tính Đạo Hàm của (y = căn(2x + 5))

1. Xác định hàm u: (u = 2x + 5)
2. Tính đạo hàm của u: (u’ = 2)
3. Áp dụng công thức đạo hàm của căn u:

d/dx (căn(2x + 5)) = 2 / (2 * căn(2x + 5)) = 1 / căn(2x + 5)

Bài Tập 2: Tính Đạo Hàm của (y = x * căn(x^2 + 2x + 1))

1. Sử dụng quy tắc tích và hàm hợp:

d/dx (x * căn(x^2 + 2x + 1)) = x * d/dx (căn(x^2 + 2x + 1)) + căn(x^2 + 2x + 1) * d/dx (x)

2. Tính đạo hàm của từng phần:

= x * (2x + 2) / (2 * căn(x^2 + 2x + 1)) + căn(x^2 + 2x + 1)
= (x(x + 1)) / căn(x^2 + 2x + 1) + căn(x^2 + 2x + 1)

Trên đây là một số kiến thức cơ bản và ví dụ về đạo hàm căn x. Hy vọng rằng thông tin này sẽ giúp các bạn hiểu rõ hơn về cách tính và ứng dụng của đạo hàm căn x trong các bài toán toán học và thực tiễn.

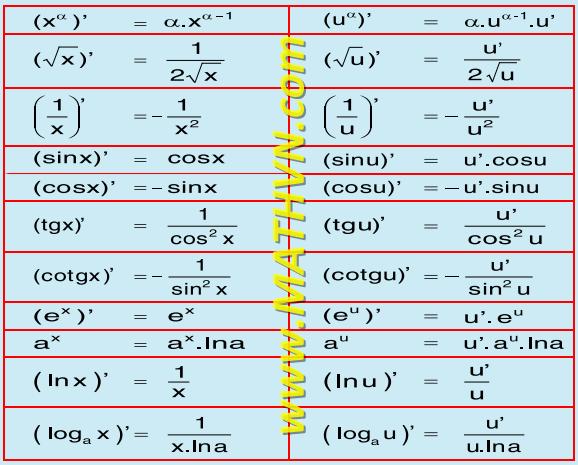
Đạo Hàm Căn x - Image Source: [ispacedanang.edu.vn](https://ispacedanang.edu.vn/wp-content/uploads/2024/06/can-x-dao-ham-bang.jpg)

Nguồn: https://ispacedanang.edu.vn
Danh mục: Học tập