Đây là hướng dẫn sử dụng thuật toán Dijkstra để tìm đường đi ngắn nhất trên đồ thị. Thuật toán Dijkstra là một trong những thuật toán cơ bản và quan trọng nhất trong lĩnh vực này. Nó được sử dụng để tìm đường đi ngắn nhất từ một điểm đến một điểm khác trên đồ thị với các trọng số không âm.
Contents
Sơ lược về bài toán đường đi ngắn nhất
Bài toán đường đi ngắn nhất là một bài toán quan trọng trong lĩnh vực khoa học máy tính. Thuật toán Dijkstra giúp chúng ta tìm ra đường đi ngắn nhất từ một điểm đến một điểm khác trên đồ thị. Điều kiện để sử dụng thuật toán này là các trọng số của các cạnh trên đồ thị phải là các số không âm.
Bạn đang xem: #Team4T's Coding Site
.png)
Thuật toán Dijkstra
Tổ chức dữ liệu
Xem thêm : Bài 8: Các kiểu dữ liệu và cách sử dụng
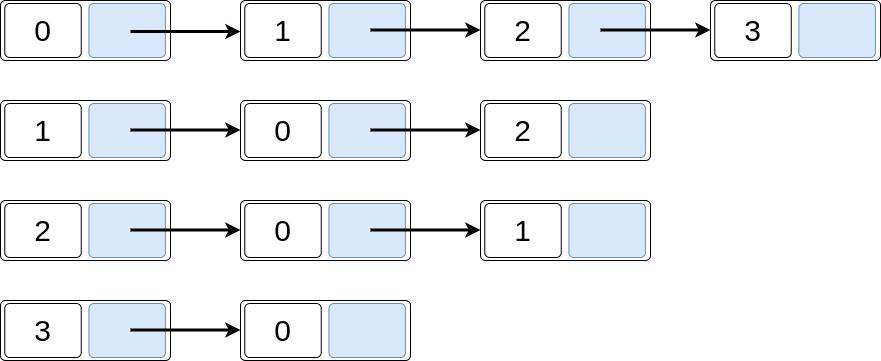
Trước khi thực hiện thuật toán Dijkstra, ta cần xây dựng một mảng để lưu trữ đường đi ngắn nhất từ một điểm đến tất cả các điểm khác trên đồ thị. Ban đầu, ta gán giá trị của mỗi đường đi là vô cùng (INF).
Quá trình thực hiện thuật toán
Quá trình thực hiện thuật toán Dijkstra sẽ diễn ra như sau:
- Chọn một điểm chưa được duyệt và có đường đi ngắn nhất từ điểm xuất phát tới nó là nhỏ nhất.
- Từ điểm đó, loang đường đi ra tất cả các đỉnh kề cận, và cập nhật lại đường đi ngắn nhất tới các đỉnh đó nếu có đường đi mới tốt hơn.
- Nếu vẫn còn điểm chưa được duyệt, ta quay lại bước 1.
Cải tiến thuật toán
Xem thêm : Cảnh bảo việc giả mạo Thanh Giang
Với phương pháp tham lam, độ phức tạp của thuật toán là O(V), với V là số lượng đỉnh trên đồ thị. Tuy nhiên, ta có thể cải tiến quá trình này thông qua hàng đợi ưu tiên, giúp tìm kiếm đỉnh tiếp theo nhanh hơn. Độ phức tạp của thuật toán sau cải tiến là O(V*log V).

Ví dụ về bài toán
Một bài toán tham khảo để áp dụng thuật toán Dijkstra là Codeforces 20C. Bài toán này yêu cầu tìm đường đi ngắn nhất từ đỉnh 1 tới đỉnh N trên một đồ thị có trọng số. Nếu không có đường đi, ta in ra -1. Nếu có nhiều đường đi cùng trả về một giá trị tối ưu, ta có thể tùy chọn đường đi.
Kết luận
Thuật toán Dijkstra là một công cụ hữu ích trong việc tìm đường đi ngắn nhất trên đồ thị. Với cách cài đặt và cải tiến phù hợp, ta có thể tìm ra giải pháp tối ưu cho các bài toán tương tự.
Nguồn: https://ispacedanang.edu.vn
Danh mục: Học tập