Danh sách kề (Adjacency list)

Trong bài viết này, chúng ta sẽ cùng tìm hiểu về danh sách kề – một cấu trúc dữ liệu quan trọng trong lập trình. Chúng ta sẽ tìm hiểu từng bước cụ thể để hiểu cấu trúc dữ liệu danh sách kề, ưu và nhược điểm của nó và những ứng dụng trong thực tế. Hơn nữa, chúng ta sẽ cùng nhau cài đặt cấu trúc danh sách kề bằng ngôn ngữ C/C++.

Có thể bạn quan tâm

Để hiểu rõ bài viết này, bạn nên có kiến thức về:

Bạn đang xem: Danh sách kề (Adjacency list)

Con trỏ
Danh sách liên kết

Chúng ta cùng tìm hiểu về danh sách kề nhé!

Contents

1 Danh sách kề là gì?
- 1.1 Ưu điểm của danh sách kề
- 1.2 Nhược điểm của danh sách kề
2 Cài đặt danh sách kề

Danh sách kề là gì?

Danh sách kề (Adjacency list) biểu diễn một đồ thị (graph) dưới dạng một mảng các danh sách liên kết. Trong đó, chỉ số mảng đại diện cho đỉnh của đồ thị và các phần tử trong danh sách liên kết của đỉnh đó là cách đỉnh có kết nối với đỉnh đó.

Lấy ví dụ với một đồ thị dưới đây:

Ví dụ một đồ thị vô hướng

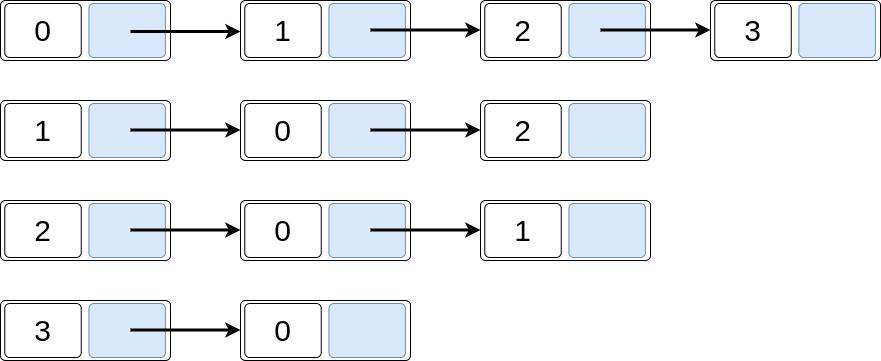
Với đồ thị trên, chúng ta có thể biểu diễn nó trong bộ nhớ máy tính dưới dạng một mảng các danh sách liên kết như hình vẽ dưới đây:

Biểu diễn đồ thị dưới dạng mảng của các danh sách liên kết

Đồ thị của chúng ta có 4 đỉnh (0, 1, 2 và 3). Do đó, chúng ta cũng sẽ có 4 danh sách liên kết tương ứng với 4 đỉnh đó. Trong mỗi danh sách liên kết, các Node đại diện cho các đỉnh có kết nối với Node head.

Ví dụ:

Danh sách liên kết cho đỉnh 0 (head) có 3 Node phía sau tương ứng là (1, 2 và 3), cho thấy các cặp đỉnh (0, 1), (0, 2) và (0, 3) có kết nối.
Tương tự, danh sách liên kết của đỉnh 2 (head) có 2 Node phía sau lần lượt là (0 và 2), cho thấy các cặp đỉnh (2, 0) và (2, 1) có kết nối.

Ưu điểm của danh sách kề

So với ma trận kề (adjacency matrix), biểu diễn đồ thị dưới dạng danh sách kề giúp tiết kiệm bộ nhớ hơn. Điều này rõ ràng hơn khi đồ thị có nhiều đỉnh nhưng ít cạnh (kết nối).
Việc duyệt các đỉnh kề với một đỉnh nào đó cũng rất nhanh chóng do mỗi đỉnh chỉ kết nối với các đỉnh kề với nó.

Nhược điểm của danh sách kề

Do sử dụng danh sách liên kết, việc kiểm tra 2 đỉnh bất kỳ có kết nối hay không cần phải duyệt tuần tự từ node head, điều này chậm hơn so với việc kiểm tra nếu cài đặt bằng ma trận kề.

Cài đặt danh sách kề

Xem thêm : Cách dùng like (động từ)

Trong phần này, chúng ta sẽ tạo chương trình mẫu để cài đặt danh sách kề theo các quy ước sau:

Đồ thị vô hướng và không có trọng số
Danh sách liên kết đơn

Cấu trúc của danh sách kề

Do danh sách kề là một mảng của các danh sách liên kết, chúng ta cần định nghĩa cấu trúc Node để đại diện cho các phần tử của danh sách liên kết:

struct Node {
    int vertex;
    struct Node *next;
};

Ngoài ra, chúng ta cần định nghĩa cấu trúc đồ thị: một mảng của các danh sách liên kết với số lượng đỉnh cho trước:

struct Graph {
    int numVertices; // số đỉnh
    struct Node **lists;
};

Chúng ta sử dụng con trỏ cấp 2 struct Node** để đại diện cho mảng các danh sách liên kết. Mỗi danh sách liên kết lại là một con trỏ kiểu Node.

Sau này, khi biết số lượng đỉnh, chúng ta sẽ cấp phát bộ nhớ động cho mảng này để đảm bảo đủ dung lượng sử dụng.

Các hàm khởi tạo

Chúng ta cần một hàm khởi tạo Node cho danh sách liên kết để có thể thêm Node vào danh sách liên kết khi cần:

// Tạo mới 1 Node
struct Node *createNode(int val) {
    // cấp phát bộ nhớ
    struct Node *newNode = malloc(sizeof(struct Node));
    // gán giá trị đỉnh
    newNode->vertex = val;
    // cho next trỏ tới NULL, tránh nó trỏ lung tung (giá trị rác)
    newNode->next = NULL;
    return newNode;
}

Và đương nhiên không thể thiếu, chúng ta cần một hàm khởi tạo cho đồ thị. Hàm này sẽ thực hiện các công việc sau:

Cấp phát bộ nhớ cho đồ thị
Cấp phát bộ nhớ cho mảng các danh sách liên kết của đồ thị

Khởi tạo đỉnh ban đầu cho mỗi danh sách liên kết

// Tạo một đồ thị
struct Graph *createAGraph(int vertices) {
  // Cấp phát bộ nhớ cho đồ thị
  struct Graph *graph = malloc(sizeof(struct Graph));
  // Gán thông tin số đỉnh cho đồ thị
  graph->numVertices = vertices;
  // Cấp phát bộ nhớ cho mảng các danh sách liên kết dựa trên số lượng đỉnh
  graph->lists = malloc(vertices * sizeof(struct Node *));
  // Hiện tại, mảng các danh sách liên kết chưa có giá trị
  // Chúng ta sẽ gán cho các danh sách này tương ứng là node đỉnh của nó
  // Sau này, ta sẽ thêm các đỉnh có kết nối với nó vào sau Node đỉnh này
  int i;
  struct Node *temp;
  for (i = 0; i < vertices; i++) {
      temp = createNode(i);
      // i chính là đỉnh của DSLK
      graph->lists[i] = temp;
  }
  return graph;
}

Tạo kết nối giữa 2 đỉnh

Nếu 2 đỉnh s và d có kết nối với nhau, chúng ta sẽ thêm Node d vào danh sách liên kết có đỉnh là s và ngược lại:

// Tạo kết nối giữa 2 đỉnh
void addEdge(struct Graph *graph, int s, int d) {
    // Thêm kết nối từ s đến d
    // Tạo node mới
    struct Node *newNode = createNode(d);
    // Node mới ta sẽ chèn vào đầu danh sách liên kết cho nhanh.
    // Vì chèn vào cuối phải duyệt tới cuối
    // Cho node mới làm head của DSLK, nên cần cho next của nó trỏ tới next mà head hiện tại đang trỏ
    newNode->next = graph->lists[s]->next;
    // Cập nhật head mới cho DSLK
    graph->lists[s]->next = newNode;

    // Thêm kết nối từ d đến s
    // Quá trình tương tự như trên
    newNode = createNode(s);
    newNode->next = graph->lists[d]->next;
    graph->lists[d]->next = newNode;
}

Duyệt danh sách kề

Xem thêm : Đề ôn thi VIOEDU lớp 4 cấp Trường năm 2023 – 2024 ôn thi theo chủ điểm

Việc duyệt danh sách kề thực chất là việc lặp lại quá trình duyệt danh sách liên kết đơn:

// Duyệt danh sách kề
void printGraph(struct Graph *graph) {
    int i;
    // Duyệt qua từng danh sách liên kết
    for (i = 0; i < graph->numVertices; i++) {
        // Tại mỗi danh sách liên kết, tạo con trỏ làm biến tạm để duyệt
        // Nếu dùng luôn head để duyệt sẽ mất dấu head của DSLK
        printf("Đỉnh %d có kết nối với: ", graph->lists[i]->vertex);
        struct Node *temp = graph->lists[i]->next;
        // duyệt DSLK cho tới khi NULL
        while (temp) {
            printf("%d ", temp->vertex);
            temp = temp->next;
        }
        printf("n");
    }
}

Source code danh sách kề đầy đủ

Cuối cùng, chúng ta sẽ bổ sung hàm main và thực thi chương trình. Dưới đây là toàn bộ mã nguồn cài đặt danh sách kề:

#include 
#include 

struct Node {
    int vertex;
    struct Node *next;
};

struct Graph {
    int numVertices; // số đỉnh
    struct Node **lists;
};

// Tạo mới 1 Node
struct Node *createNode(int val) {
    // cấp phát bộ nhớ
    struct Node *newNode = malloc(sizeof(struct Node));
    // gán giá trị đỉnh
    newNode->vertex = val;
    // cho next trỏ tới NULL, tránh nó trỏ lung tung (giá trị rác)
    newNode->next = NULL;
    return newNode;
}

// Tạo một đồ thị
struct Graph *createAGraph(int vertices) {
    // Cấp phát bộ nhớ cho đồ thị
    struct Graph *graph = malloc(sizeof(struct Graph));
    // Gán thông tin số đỉnh cho đồ thị
    graph->numVertices = vertices;
    // Cấp phát bộ nhớ cho mảng các danh sách liên kết dựa trên số lượng đỉnh
    graph->lists = malloc(vertices * sizeof(struct Node *));
    // Hiện tại, mảng các danh sách liên kết chưa có giá trị
    // Chúng ta sẽ gán cho các danh sách này tương ứng là node đỉnh của nó
    // Sau này, ta sẽ thêm các đỉnh có kết nối với nó vào sau Node đỉnh này
    int i;
    struct Node *temp;
    for (i = 0; i < vertices; i++) {
        temp = createNode(i);
        // i chính là đỉnh của DSLK
        graph->lists[i] = temp;
    }
    return graph;
}

// Tạo kết nối giữa 2 đỉnh
void addEdge(struct Graph *graph, int s, int d) {
    // Thêm kết nối từ s đến d
    // Tạo node mới
    struct Node *newNode = createNode(d);
    // Node mới ta sẽ chèn vào đầu danh sách liên kết cho nhanh.
    // Vì chèn vào cuối phải duyệt tới cuối
    // Cho node mới làm head của DSLK, nên cần cho next của nó trỏ tới next mà head hiện tại đang trỏ
    newNode->next = graph->lists[s]->next;
    // Cập nhật head mới cho DSLK
    graph->lists[s]->next = newNode;

    // Thêm kết nối từ d đến s
    // Quá trình tương tự như trên
    newNode = createNode(s);
    newNode->next = graph->lists[d]->next;
    graph->lists[d]->next = newNode;
}

// Duyệt danh sách kề
void printGraph(struct Graph *graph) {
    int i;
    // Duyệt qua từng danh sách liên kết
    for (i = 0; i < graph->numVertices; i++) {
        // Tại mỗi danh sách liên kết, tạo con trỏ làm biến tạm để duyệt
        // Nếu dùng luôn head để duyệt sẽ mất dấu head của DSLK
        printf("Đỉnh %d có kết nối với: ", graph->lists[i]->vertex);
        struct Node *temp = graph->lists[i]->next;
        // duyệt DSLK cho tới khi NULL
        while (temp) {
            printf("%d ", temp->vertex);
            temp = temp->next;
        }
        printf("n");
    }
}

int main() {
    struct Graph *graph = createAGraph(4);
    addEdge(graph, 0, 1);
    addEdge(graph, 0, 2);
    addEdge(graph, 0, 3);
    addEdge(graph, 1, 2);
    printGraph(graph);
    return 0;
}

Trong hàm main, chúng ta sẽ biểu diễn một đồ thị gồm 4 đỉnh và các kết nối như hình vẽ ở ví dụ trước. Dưới đây là kết quả khi chạy chương trình:

Đỉnh 0 có kết nối với: 3 2 1
Đỉnh 1 có kết nối với: 2 0
Đỉnh 2 có kết nối với: 1 0
Đỉnh 3 có kết nối với: 0

Về bản chất, danh sách kề là cấu trúc dữ liệu để biểu diễn đồ thị vào bộ nhớ máy tính. Nên chính xác thì ta nên nói ứng dụng của đồ thị.

Ở mục này, mình chia sẻ thêm một source code sử dụng danh sách kề để biểu diễn mối quan hệ giữa các sinh viên trong một lớp học: Các sinh viên cùng lớp sẽ có kết nối với nhau.

#include 
#include 
#include 

typedef struct SinhVien {
    char MaSV[20];
    char Ho[50];
    char Ten[20];
    char GioiTinh[5];
    int NamSinh;
    char Nganh[100];
    char Lop[20];
} SV;

void NhapChuoi(char *s, int n) {
    char *p;
    fgets(s, n, stdin);
    if ((p = strchr(s, 'n')) != NULL) {
        *p = '';
    }
}

SV Nhap1SV() {
    SV sv;
    printf("Nhập Mã SV: ");
    NhapChuoi(sv.MaSV, 20);
    printf("Nhập họ SV: ");
    NhapChuoi(sv.Ho, 50);
    printf("Nhập tên SV: ");
    NhapChuoi(sv.Ten, 20);
    printf("Nhập giới tính: ");
    NhapChuoi(sv.GioiTinh, 5);
    printf("Nhập năm sinh: ");
    scanf("%d", &sv.NamSinh);
    getchar();
    printf("Nhập ngành: ");
    NhapChuoi(sv.Nganh, 100);
    printf("Nhập lớp: ");
    NhapChuoi(sv.Lop, 20);
    return sv;
}

void Xuat1SV(SV sv) {
    printf("Mã: %sn", sv.MaSV);
    printf("Họ: %sn", sv.Ho);
    printf("Tên: %sn", sv.Ten);
    printf("Giới tính: %sn", sv.GioiTinh);
    printf("Năm sinh: %dn", sv.NamSinh);
    printf("Ngành: %sn", sv.Nganh);
    printf("Lớp: %sn", sv.Lop);
}

typedef struct Node {
    struct SinhVien data;
    struct Node *next;
} Node;

typedef struct DoThi {
    int soDinh;
    struct Node** dsPhanTu;
} DoThi;

// Tạo mới Node
struct Node* TaoNode(SV sv) {
    struct Node* newNode = (struct Node*)malloc(sizeof(Node));
    newNode->data = sv;
    newNode->next = NULL;
    return newNode;
}

// Tạo một đồ thị
DoThi* Tao1DoThi(int soDinh) {
    DoThi* doThi = (struct DoThi*) malloc(sizeof(DoThi));
    doThi->soDinh = soDinh;
    doThi->dsPhanTu = (struct Node**)malloc(soDinh * sizeof(Node*));
    int i;
    for (i = 0; i < soDinh; i++) doThi->dsPhanTu[i] = NULL;
    return doThi;
}

void ThemSinhVienVaoDoThi(DoThi *doThi) {
    int i;
    for (i = 0; i < doThi->soDinh; i++){
        SV sv = Nhap1SV();
        Node *node = TaoNode(sv);
        doThi->dsPhanTu[i] = node;
        printf("==================n");
    }
}

void ThemCanh(DoThi *doThi, int s, int d) {
    struct Node *newNode = TaoNode(doThi->dsPhanTu[d]->data);
    newNode->next = doThi->dsPhanTu[s]->next;
    doThi->dsPhanTu[s]->next = newNode;

    newNode = TaoNode(doThi->dsPhanTu[s]->data);
    newNode->next = doThi->dsPhanTu[d]->next;
    doThi->dsPhanTu[d]->next = newNode;
}

int CungLop(SV a, SV b) {
    if (strcmp(a.Lop, b.Lop) == 0) {
        return 1;
    }
    return 0;
}

void TaoKetNoiTheoLop(DoThi *doThi) {
    int i, j;
    for (i = 0; i < doThi->soDinh - 1; i++) {
        for (j = i+1; j < doThi->soDinh; j++) {
            if (CungLop(doThi->dsPhanTu[i]->data, doThi->dsPhanTu[j]->data)) {
                ThemCanh(doThi, i, j);
            }
        }
    }
}

void InDanhSachSV(DoThi *doThi) {
    int i;
    printf("%10s%20s%10s%10s%10s%50s%20sn", "Mã SV", "Họ", "Tên", "Giới tính", "Năm sinh", "Ngành", "Lớp");
    for (i = 0; i < doThi->soDinh; i++) {
        SV sv = doThi->dsPhanTu[i]->data;
        printf("%10s%20s%10s%10s%10d%50s%20sn", sv.MaSV, sv.Ho, sv.Ten, sv.GioiTinh, sv.NamSinh, sv.Nganh, sv.Lop);
    }
}

void DuyetDoThi(DoThi *doThi) {
    int i;
    for (i = 0; i < doThi->soDinh; i++) {
        Xuat1SV(doThi->dsPhanTu[i]->data);
        printf("=> DS cùng lớp (Mã SV): ");
        struct Node *temp = doThi->dsPhanTu[i];
        temp = temp->next;
        while(temp) {
            printf("%s", temp->data.MaSV);
            temp = temp->next;
            if (temp) {
                printf(", ");
            }
        }
        printf("n=======================n");
    }
}

int main() {
    int soLuong;
    printf("Nhập số lượng sinh viên: ");
    scanf("%d", &soLuong);
    DoThi *doThi = Tao1DoThi(soLuong);
    getchar();
    ThemSinhVienVaoDoThi(doThi);
    TaoKetNoiTheoLop(doThi);
    printf("Danh sách SV hiện có: n");
    InDanhSachSV(doThi);
    printf("Kết quả duyệt danh sách kề: n");
    DuyetDoThi(doThi);
    return 0;
}

Kết quả thực thi:

Nhập số lượng sinh viên: 4
Nhập Mã SV: 1
Nhập họ SV: 1
Nhập tên SV: 1
Nhập giới tính: 1
Nhập năm sinh: 1
Nhập ngành: 1
Nhập lớp: 1
==================
Nhập Mã SV: 2
Nhập họ SV: 2
Nhập tên SV: 2
Nhập giới tính: 2
Nhập năm sinh: 2
Nhập ngành: 2
Nhập lớp: 2
==================
Nhập Mã SV: 3
Nhập họ SV: 3
Nhập tên SV: 3
Nhập giới tính: 3
Nhập năm sinh: 3
Nhập ngành: 3
Nhập lớp: 2
==================
Nhập Mã SV: 4
Nhập họ SV: 4
Nhập tên SV: 4
Nhập giới tính: 4
Nhập năm sinh: 4
Nhập ngành: 4
Nhập lớp: 1
==================
Danh sách SV hiện có:
   Mã SV                  Họ       Tên Giới tính Năm sinh                                             Ngành                 Lớp
       1                  1        1         1        1                                                  1                  1
       2                  2        2         2        2                                                  2                  2
       3                  3        3         3        3                                                  3                  2
       4                  4        4         4        4                                                  4                  1
Kết quả duyệt danh sách kề:
Mã: 1
Họ: 1
Tên: 1
Giới tính: 1
Năm sinh: 1
Ngành: 1
Lớp: 1
=> DS cùng lớp (Mã SV): 4
=======================
Mã: 2
Họ: 2
Tên: 2
Giới tính: 2
Năm sinh: 2
Ngành: 2
Lớp: 2
=> DS cùng lớp (Mã SV): 3
=======================
Mã: 3
Họ: 3
Tên: 3
Giới tính: 3
Năm sinh: 3
Ngành: 3
Lớp: 2
=> DS cùng lớp (Mã SV): 2
=======================
Mã: 4
Họ: 4
Tên: 4
Giới tính: 4
Năm sinh: 4
Ngành: 4
Lớp: 1
=> DS cùng lớp (Mã SV): 1
=======================

Bài viết tới đây là kết thúc, xin chào và hẹn gặp lại các bạn ở các bài viết tiếp theo!

Theo dõi Lập Trình Không Khó để không bỏ lỡ các bài học bổ ích:

Nguồn: https://ispacedanang.edu.vn
Danh mục: Học tập