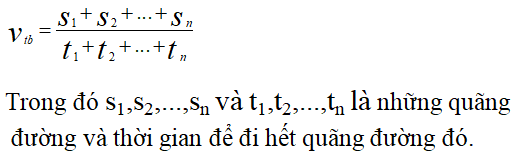Chủ đề tính chất nào sau đây là của vận tốc: Tính chất nào sau đây là của vận tốc? Bài viết này sẽ giúp bạn hiểu rõ khái niệm vận tốc, các tính chất đặc trưng của nó và những ứng dụng trong thực tế. Cùng tìm hiểu cách tính vận tốc, phân biệt với tốc độ, và những ví dụ minh họa dễ hiểu. Hãy cùng khám phá để nắm vững kiến thức về vận tốc trong vật lý học.
Mục lục
Tính chất của vận tốc
Vận tốc là một đại lượng vật lý có tính chất vectơ, bao gồm cả độ lớn và hướng di chuyển của vật thể. Nó không chỉ đặc trưng cho tốc độ thay đổi vị trí của vật thể mà còn xác định phương hướng chuyển động. Dưới đây là các tính chất chính của vận tốc:
Tính chất cơ bản của vận tốc
- Vận tốc là một đại lượng vectơ: Để xác định vận tốc, chúng ta cần biết cả tốc độ (độ lớn của vận tốc) và hướng của chuyển động.
- Vận tốc có thể thay đổi: Nếu tốc độ hoặc hướng chuyển động thay đổi, vận tốc cũng sẽ thay đổi, dẫn đến sự xuất hiện của gia tốc.
- Vận tốc trung bình: Được tính theo công thức: \[ v_{tb} = \frac{\Delta x}{\Delta t} \] trong đó \(\Delta x\) là độ dời (m), và \(\Delta t\) là thời gian chuyển động (s).
- Vận tốc tức thời: Biểu thị tốc độ và hướng chuyển động tại một thời điểm cụ thể, tính theo công thức: \[ \mathbf{v} = \frac{d\mathbf{r}}{dt} \] với \(r\) là vị trí của vật thể như một hàm số của thời gian.
Công thức tính vận tốc
Vận tốc của một vật thể có thể được tính bằng công thức:
- \[ v = \frac{s}{t} \] trong đó \(v\) là vận tốc, \(s\) là quãng đường đi được và \(t\) là thời gian di chuyển.
Đơn vị đo vận tốc
Đơn vị đo lường vận tốc thông thường là mét trên giây (m/s) hoặc kilômét trên giờ (km/h). Trong Hệ đo lường quốc tế (SI), m/s là đơn vị chính thức.
Tính chất tương đối của vận tốc
Vận tốc có tính chất tương đối vì nó phụ thuộc vào hệ quy chiếu. Trong cùng một chuyển động, vận tốc của vật thể có thể khác nhau khi quan sát từ các hệ quy chiếu khác nhau. Ví dụ, một vật chuyển động có thể có vận tốc bằng 0 so với chính nó nhưng khác so với một vật khác.
Ứng dụng của vận tốc
- Vận tốc giúp mô tả chuyển động của vật thể trong không gian, được sử dụng trong các ngành khoa học như vật lý, thiên văn học, và kỹ thuật.
- Trong đời sống hàng ngày, vận tốc được sử dụng để đo tốc độ di chuyển của các phương tiện giao thông như ô tô, xe máy, tàu thuyền, v.v.

.png)
1. Khái niệm về Vận tốc
Vận tốc là một đại lượng vật lý đặc trưng cho sự thay đổi vị trí của một vật theo thời gian trong một hệ quy chiếu nhất định. Vận tốc không chỉ bao gồm độ lớn mà còn bao gồm hướng chuyển động, do đó nó được biểu diễn dưới dạng một vectơ.
Vận tốc được ký hiệu là \(\vec{v}\), với công thức tính tổng quát:
\[ \vec{v} = \frac{\Delta \vec{s}}{\Delta t} \]
Trong đó:
- \(\Delta \vec{s}\): Độ dời (quãng đường di chuyển có hướng)
- \(\Delta t\): Khoảng thời gian di chuyển
Đơn vị đo của vận tốc trong hệ SI thường là mét trên giây (m/s), ngoài ra còn có thể sử dụng đơn vị kilômét trên giờ (km/h).
| Đơn vị | Ký hiệu | Mối quan hệ |
|---|---|---|
| mét/giây | m/s | \(1 \, m/s = 3,6 \, km/h\) |
| kilômét/giờ | km/h | \(1 \, km/h = 0,28 \, m/s\) |
Vận tốc có tính chất tương đối, nghĩa là nó có thể thay đổi phụ thuộc vào hệ quy chiếu mà ta đang quan sát. Ví dụ, một chiếc xe có thể có vận tốc khác nhau khi quan sát từ các phương tiện hoặc điểm đứng khác nhau.
Vận tốc tức thời là vận tốc của vật tại một thời điểm cụ thể, được tính theo công thức:
\[ v = \lim_{\Delta t \to 0} \frac{\Delta s}{\Delta t} = \frac{ds}{dt} \]
Trong đó, ds là độ dời rất nhỏ trong khoảng thời gian rất nhỏ dt.
2. Tính chất của Vận tốc
Vận tốc có một số tính chất đặc trưng giúp phân biệt nó với các đại lượng khác trong vật lý. Dưới đây là những tính chất cơ bản của vận tốc:
-
Vận tốc là một đại lượng vectơ:
Vận tốc không chỉ có độ lớn mà còn có hướng. Hướng của vectơ vận tốc luôn trùng với hướng chuyển động của vật. Vì vậy, để mô tả vận tốc một cách đầy đủ, chúng ta cần xác định cả độ lớn và hướng của nó.
-
Độ lớn của vận tốc:
Độ lớn của vận tốc cho biết vật di chuyển nhanh hay chậm. Độ lớn này còn được gọi là tốc độ và được tính theo công thức:
\[ v = \frac{S}{t} \]
Trong đó:
- \(S\): quãng đường đi được
- \(t\): thời gian đi hết quãng đường đó
-
Vận tốc có tính tương đối:
Vận tốc của một vật không phải là cố định, nó thay đổi tùy thuộc vào hệ quy chiếu mà ta sử dụng để quan sát vật. Điều này có nghĩa là một vật có thể có vận tốc khác nhau khi được quan sát từ các điểm nhìn khác nhau.
-
Vận tốc phụ thuộc vào thời gian:
Vận tốc của một vật có thể thay đổi theo thời gian. Khi đó, chúng ta cần sử dụng khái niệm vận tốc tức thời để mô tả vận tốc của vật tại một thời điểm cụ thể:
\[ v(t) = \frac{ds}{dt} \]
-
Vận tốc trung bình và vận tốc tức thời:
Vận tốc trung bình là vận tốc được tính trong suốt khoảng thời gian mà vật di chuyển, trong khi đó, vận tốc tức thời là vận tốc tại một thời điểm cụ thể.

3. Công thức tính Vận tốc
Công thức tính vận tốc là một phần quan trọng trong việc hiểu và áp dụng các nguyên tắc của vật lý. Vận tốc được xác định dựa trên mối quan hệ giữa quãng đường đi được và thời gian di chuyển của vật thể.
3.1. Công thức tổng quát của vận tốc
Vận tốc trung bình của một vật được tính bằng công thức:
\[ v = \frac{S}{t} \]
Trong đó:
- \(v\): Vận tốc trung bình (m/s hoặc km/h)
- \(S\): Quãng đường đi được (m hoặc km)
- \(t\): Thời gian di chuyển (s hoặc h)
3.2. Công thức tính vận tốc tức thời
Vận tốc tức thời của một vật là vận tốc tại một thời điểm cụ thể và được xác định bằng đạo hàm của độ dời theo thời gian:
\[ v(t) = \frac{ds}{dt} \]
Trong đó:
- \(v(t)\): Vận tốc tức thời tại thời điểm \(t\)
- \(ds\): Độ dời rất nhỏ
- \(dt\): Khoảng thời gian rất nhỏ
3.3. Công thức tính vận tốc trong các trường hợp đặc biệt
Trong một số trường hợp đặc biệt, vận tốc có thể được tính như sau:
- Vận tốc trong chuyển động đều: Khi vật di chuyển với vận tốc không đổi, công thức tính vận tốc vẫn là \( v = \frac{S}{t} \).
- Vận tốc trung bình trong chuyển động không đều: Đối với chuyển động không đều, vận tốc trung bình được tính bằng công thức:
\[ v_{tb} = \frac{S_{1} + S_{2} + ... + S_{n}}{t_{1} + t_{2} + ... + t_{n}} \]
3.4. Đơn vị đo của vận tốc
Đơn vị đo vận tốc trong hệ SI là mét trên giây (m/s), tuy nhiên, trong đời sống hàng ngày, người ta thường sử dụng kilômét trên giờ (km/h). Mối quan hệ giữa hai đơn vị này là:
\[ 1 \, m/s = 3,6 \, km/h \]
3.5. Bảng quy đổi vận tốc
| Đơn vị | Ký hiệu | Quy đổi |
|---|---|---|
| Mét trên giây | m/s | 1 m/s = 3,6 km/h |
| Kilômét trên giờ | km/h | 1 km/h = 0,28 m/s |

4. Bài tập Vận dụng
Để củng cố kiến thức về vận tốc, dưới đây là một số bài tập vận dụng giúp bạn hiểu rõ hơn về các khái niệm và công thức đã học.
Bài tập 1: Tính vận tốc trung bình
Một chiếc xe di chuyển từ điểm A đến điểm B với quãng đường \( S = 120 \, km \) trong thời gian \( t = 2 \, giờ \). Hãy tính vận tốc trung bình của xe.
Lời giải:
- Sử dụng công thức: \[ v = \frac{S}{t} \]
- Thay số: \[ v = \frac{120 \, km}{2 \, giờ} = 60 \, km/h \]
- Vậy vận tốc trung bình của xe là \( 60 \, km/h \).
Bài tập 2: Vận tốc tức thời
Một vật chuyển động có phương trình \( s(t) = 3t^2 + 2t \) (trong đó \( s \) tính bằng mét, \( t \) tính bằng giây). Tính vận tốc tức thời của vật tại thời điểm \( t = 2 \, s \).
Lời giải:
- Vận tốc tức thời là đạo hàm của độ dời theo thời gian: \[ v(t) = \frac{ds}{dt} \]
- Ta có: \[ v(t) = \frac{d}{dt}(3t^2 + 2t) = 6t + 2 \]
- Thay \( t = 2 \, s \): \[ v(2) = 6(2) + 2 = 14 \, m/s \]
- Vậy vận tốc tức thời tại \( t = 2 \, s \) là \( 14 \, m/s \).
Bài tập 3: Vận tốc trong chuyển động không đều
Một vật di chuyển trên quãng đường gồm hai đoạn: đoạn đầu dài \( S_1 = 50 \, km \) trong thời gian \( t_1 = 1 \, giờ \), và đoạn sau dài \( S_2 = 30 \, km \) trong thời gian \( t_2 = 0,5 \, giờ \). Hãy tính vận tốc trung bình của vật trên toàn bộ quãng đường.
Lời giải:
- Tổng quãng đường: \[ S = S_1 + S_2 = 50 \, km + 30 \, km = 80 \, km \]
- Tổng thời gian: \[ t = t_1 + t_2 = 1 \, giờ + 0,5 \, giờ = 1,5 \, giờ \]
- Vận tốc trung bình: \[ v_{tb} = \frac{S}{t} = \frac{80 \, km}{1,5 \, giờ} = 53,33 \, km/h \]
- Vậy vận tốc trung bình trên toàn bộ quãng đường là \( 53,33 \, km/h \).

5. Ứng dụng thực tế của Vận tốc
Vận tốc không chỉ là một khái niệm lý thuyết trong vật lý mà còn có nhiều ứng dụng thực tế trong cuộc sống hàng ngày và các lĩnh vực công nghệ, khoa học. Dưới đây là một số ứng dụng cụ thể của vận tốc:
5.1. Giao thông và Vận tải
- Tính toán thời gian di chuyển: Vận tốc giúp ước tính thời gian di chuyển từ điểm A đến điểm B, hỗ trợ trong việc lập kế hoạch giao thông và vận tải.
- Quản lý vận tốc: Trong giao thông, việc kiểm soát vận tốc của phương tiện giúp đảm bảo an toàn và hiệu quả trong vận chuyển hành khách và hàng hóa.
5.2. Thể thao
- Đo lường thành tích: Vận tốc được sử dụng để đánh giá và cải thiện thành tích của các vận động viên trong các môn thể thao như chạy bộ, đua xe, bơi lội.
- Kỹ thuật tập luyện: Các huấn luyện viên sử dụng vận tốc để thiết kế các bài tập giúp vận động viên tối ưu hóa khả năng và tốc độ của mình.
5.3. Hàng không và Vũ trụ
- Điều khiển máy bay và tên lửa: Vận tốc đóng vai trò quan trọng trong việc tính toán quỹ đạo và điều khiển các phương tiện hàng không, giúp đạt được độ chính xác cao trong điều hướng.
- Khám phá không gian: Các nhà khoa học sử dụng vận tốc để tính toán thời gian và quãng đường trong các nhiệm vụ khám phá vũ trụ.
5.4. Sản xuất và Công nghiệp
- Tối ưu hóa quy trình sản xuất: Vận tốc được sử dụng để đánh giá hiệu suất của dây chuyền sản xuất, từ đó cải thiện tốc độ và chất lượng sản phẩm.
- Đo lường và điều khiển: Trong các hệ thống tự động hóa, vận tốc của các bộ phận máy móc cần được kiểm soát chặt chẽ để đảm bảo hiệu quả và an toàn trong sản xuất.
5.5. Khoa học và Nghiên cứu
- Thí nghiệm vật lý: Trong các thí nghiệm nghiên cứu, vận tốc là đại lượng quan trọng để đo lường và phân tích các hiện tượng vật lý.
- Phân tích chuyển động: Vận tốc được sử dụng trong các nghiên cứu về chuyển động của các đối tượng, từ các hạt vi mô đến các thiên thể trong vũ trụ.
Nhờ vào vận tốc, con người có thể ứng dụng hiệu quả các nguyên tắc vật lý vào nhiều lĩnh vực khác nhau, nâng cao chất lượng cuộc sống và phát triển khoa học công nghệ.