Chủ đề cách tính vận tốc trung bình trên cả quãng đường: Tìm hiểu cách tính vận tốc trung bình trên cả quãng đường một cách dễ hiểu và chính xác. Bài viết này sẽ hướng dẫn bạn từ công thức cơ bản đến các ứng dụng thực tiễn trong đời sống, giúp bạn nắm vững kiến thức quan trọng này.
Mục lục
Cách Tính Vận Tốc Trung Bình Trên Cả Quãng Đường
Vận tốc trung bình là một đại lượng vật lý quan trọng trong nhiều bài toán thực tiễn. Để tính vận tốc trung bình trên cả quãng đường, ta có thể sử dụng các công thức toán học đơn giản. Dưới đây là các bước và ví dụ minh họa.
1. Công Thức Tính Vận Tốc Trung Bình
Vận tốc trung bình \(v_{tb}\) được tính bằng cách chia tổng quãng đường \(S\) đã đi được cho tổng thời gian \(t\) đã đi:
\[
v_{tb} = \frac{S}{t}
\]
2. Ví Dụ Minh Họa
- Ví dụ 1: Một người đi từ điểm A đến điểm B với vận tốc \(v_1 = 30 \, km/h\) và từ điểm B quay lại điểm A với vận tốc \(v_2 = 20 \, km/h\). Tính vận tốc trung bình trên cả quãng đường.
- Giải: Quãng đường từ A đến B là \(S\), thời gian đi từ A đến B là \(t_1 = \frac{S}{v_1}\), thời gian đi từ B về A là \(t_2 = \frac{S}{v_2}\).
- Ví dụ 2: Một xe ô tô di chuyển từ thành phố A đến thành phố B với vận tốc \(v_1 = 60 \, km/h\) và quay lại với vận tốc \(v_2 = 40 \, km/h\). Tính vận tốc trung bình của ô tô trên cả hành trình.
- Giải: Vận tốc trung bình của ô tô trên cả hành trình là:
Tổng quãng đường đã đi: \(2S\)
Tổng thời gian đã đi: \[
t = t_1 + t_2 = \frac{S}{v_1} + \frac{S}{v_2} = S \left(\frac{1}{v_1} + \frac{1}{v_2}\right)
\]
Vận tốc trung bình trên cả quãng đường là:
\[
v_{tb} = \frac{2S}{S \left(\frac{1}{v_1} + \frac{1}{v_2}\right)} = \frac{2v_1 v_2}{v_1 + v_2}
\]
Thay số: \(v_{tb} = \frac{2 \times 30 \times 20}{30 + 20} = \frac{1200}{50} = 24 \, km/h\).
\[
v_{tb} = \frac{2 \times 60 \times 40}{60 + 40} = \frac{4800}{100} = 48 \, km/h
\]
3. Lưu Ý Khi Tính Vận Tốc Trung Bình
- Vận tốc trung bình không phải lúc nào cũng bằng trung bình cộng của các vận tốc trên từng đoạn đường, đặc biệt khi quãng đường hoặc thời gian khác nhau.
- Cần chú ý đơn vị của vận tốc, thời gian và quãng đường để đảm bảo tính toán chính xác.
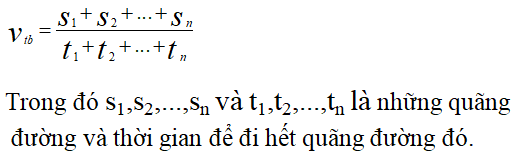
.png)
1. Giới Thiệu Về Khái Niệm Vận Tốc Trung Bình
Vận tốc trung bình là một khái niệm quan trọng trong vật lý học, được sử dụng để mô tả tốc độ di chuyển của một vật thể trên một quãng đường nhất định. Cụ thể, vận tốc trung bình được tính bằng cách chia tổng quãng đường di chuyển cho tổng thời gian di chuyển.
Trong toán học, công thức tính vận tốc trung bình thường được biểu diễn dưới dạng:
- \[v_{\text{tb}} = \frac{\Delta s}{\Delta t}\]
Trong đó:
- \(\Delta s\) là tổng quãng đường đã di chuyển.
- \(\Delta t\) là tổng thời gian đã di chuyển.
Vận tốc trung bình giúp chúng ta hiểu rõ hơn về chuyển động của các vật thể trong các bài toán cơ học, từ những chuyển động đơn giản đến những bài toán phức tạp hơn liên quan đến nhiều quãng đường khác nhau.
2. Công Thức Tính Vận Tốc Trung Bình
Vận tốc trung bình của một vật thể trên một quãng đường nhất định được xác định bằng cách chia tổng quãng đường mà vật thể đã di chuyển cho tổng thời gian di chuyển. Công thức tổng quát được thể hiện như sau:
- \[v_{\text{tb}} = \frac{S_{\text{total}}}{T_{\text{total}}}\]
Trong đó:
- \(v_{\text{tb}}\) là vận tốc trung bình.
- \(S_{\text{total}}\) là tổng quãng đường đã di chuyển.
- \(T_{\text{total}}\) là tổng thời gian di chuyển.
Nếu vật thể di chuyển trên nhiều đoạn đường với các vận tốc khác nhau, ta có thể tính vận tốc trung bình theo từng đoạn đường. Công thức tính trong trường hợp này là:
- \[v_{\text{tb}} = \frac{\sum_{i=1}^n S_i}{\sum_{i=1}^n T_i}\]
Trong đó:
- \(S_i\) là quãng đường di chuyển trên đoạn \(i\).
- \(T_i\) là thời gian di chuyển trên đoạn \(i\).
- \(n\) là số đoạn đường khác nhau.
Ví dụ, nếu một vật thể di chuyển 100 km trong 2 giờ, sau đó di chuyển thêm 50 km trong 1 giờ, vận tốc trung bình của cả quãng đường sẽ được tính như sau:
- \[v_{\text{tb}} = \frac{100 \, \text{km} + 50 \, \text{km}}{2 \, \text{giờ} + 1 \, \text{giờ}} = \frac{150 \, \text{km}}{3 \, \text{giờ}} = 50 \, \text{km/giờ}\]

3. Các Bài Toán Về Vận Tốc Trung Bình
Các bài toán về vận tốc trung bình thường xoay quanh việc tính toán tốc độ di chuyển của một vật thể khi biết tổng quãng đường và tổng thời gian di chuyển. Để giải quyết những bài toán này, người học cần nắm vững công thức và hiểu rõ các yếu tố ảnh hưởng đến vận tốc trung bình.
Dưới đây là một số dạng bài toán cơ bản và ví dụ minh họa:
- Bài toán 1: Tính vận tốc trung bình khi di chuyển trên một quãng đường duy nhất.
- Ví dụ: Một xe máy di chuyển trên đoạn đường 60 km trong 2 giờ. Vận tốc trung bình của xe là bao nhiêu?
- Giải: \[v_{\text{tb}} = \frac{60 \, \text{km}}{2 \, \text{giờ}} = 30 \, \text{km/giờ}\]
- Bài toán 2: Tính vận tốc trung bình trên nhiều đoạn đường với các vận tốc khác nhau.
- Ví dụ: Một xe hơi đi từ A đến B với vận tốc 40 km/h trong 1 giờ, sau đó đi tiếp từ B đến C với vận tốc 60 km/h trong 2 giờ. Tính vận tốc trung bình trên cả quãng đường.
- Giải: \[v_{\text{tb}} = \frac{(40 \, \text{km/h} \times 1 \, \text{giờ}) + (60 \, \text{km/h} \times 2 \, \text{giờ})}{1 \, \text{giờ} + 2 \, \text{giờ}} = \frac{40 + 120}{3} = \frac{160}{3} \, \text{km/h} \approx 53.33 \, \text{km/h}\]
- Bài toán 3: Tính vận tốc trung bình khi thời gian di chuyển không đều.
- Ví dụ: Một người đi bộ với vận tốc 5 km/h trong 30 phút và sau đó tăng tốc lên 7 km/h trong 15 phút. Tính vận tốc trung bình trên cả quãng đường.
- Giải: \[v_{\text{tb}} = \frac{(5 \, \text{km/h} \times 0.5 \, \text{giờ}) + (7 \, \text{km/h} \times 0.25 \, \text{giờ})}{0.5 \, \text{giờ} + 0.25 \, \text{giờ}} = \frac{2.5 + 1.75}{0.75} \, \text{km/h} \approx 5.67 \, \text{km/h}\]
Những bài toán này không chỉ giúp người học làm quen với cách tính toán vận tốc trung bình mà còn phát triển khả năng tư duy logic và kỹ năng giải quyết vấn đề trong các tình huống thực tế.

XEM THÊM:
4. Sai Lầm Thường Gặp Khi Tính Vận Tốc Trung Bình
Khi tính toán vận tốc trung bình, nhiều người thường mắc phải một số sai lầm phổ biến dẫn đến kết quả không chính xác. Dưới đây là những sai lầm thường gặp và cách tránh chúng:
- 1. Không phân biệt giữa vận tốc trung bình và vận tốc tức thời:
Vận tốc trung bình là tổng quãng đường chia cho tổng thời gian di chuyển, trong khi vận tốc tức thời là vận tốc tại một thời điểm cụ thể. Nhiều người nhầm lẫn hai khái niệm này và áp dụng sai công thức.
- 2. Không tính tổng thời gian hoặc tổng quãng đường:
Một lỗi phổ biến là chỉ tính vận tốc cho từng đoạn đường mà quên tính tổng quãng đường và tổng thời gian. Điều này dẫn đến việc tính toán không chính xác.
- 3. Nhầm lẫn giữa các đơn vị đo:
Trong quá trình tính toán, việc không chuyển đổi đúng đơn vị đo, chẳng hạn như giữa giờ và phút hoặc giữa km và m, sẽ làm sai lệch kết quả.
- 4. Bỏ qua các yếu tố khác ảnh hưởng đến vận tốc trung bình:
Các yếu tố như địa hình, điều kiện thời tiết, hoặc dừng nghỉ có thể ảnh hưởng đến vận tốc trung bình, nhưng đôi khi bị bỏ qua trong tính toán.
Để tránh những sai lầm trên, người học cần chú ý từng bước trong quá trình tính toán và đảm bảo rằng mọi yếu tố liên quan đều được xem xét và áp dụng đúng cách.

5. Ứng Dụng Thực Tiễn Của Vận Tốc Trung Bình
Vận tốc trung bình không chỉ là một khái niệm lý thuyết trong vật lý mà còn có nhiều ứng dụng thực tiễn trong đời sống và các ngành khoa học khác nhau. Dưới đây là một số ứng dụng cụ thể:
- 1. Trong giao thông vận tải:
Vận tốc trung bình được sử dụng để tính toán thời gian cần thiết để di chuyển từ điểm A đến điểm B, giúp tối ưu hóa lộ trình và dự đoán thời gian đến nơi.
- 2. Trong thể thao:
Đối với các môn thể thao như điền kinh, đua xe, hoặc bơi lội, vận tốc trung bình của vận động viên là một chỉ số quan trọng để đánh giá hiệu suất thi đấu và cải thiện kỹ thuật.
- 3. Trong quản lý sản xuất:
Vận tốc trung bình của các dây chuyền sản xuất giúp xác định năng suất, từ đó cải thiện quy trình và tăng cường hiệu quả sản xuất.
- 4. Trong nghiên cứu khoa học:
Vận tốc trung bình là một yếu tố quan trọng trong các thí nghiệm vật lý, đặc biệt là khi nghiên cứu chuyển động của các vật thể hoặc chất lỏng.
- 5. Trong điều tra và phân tích tai nạn:
Khi điều tra các vụ tai nạn giao thông, việc xác định vận tốc trung bình của phương tiện trước tai nạn là yếu tố then chốt để hiểu rõ nguyên nhân và trách nhiệm liên quan.
Những ứng dụng trên cho thấy vận tốc trung bình là một khái niệm không thể thiếu trong nhiều lĩnh vực, giúp giải quyết các vấn đề thực tiễn một cách hiệu quả.
6. Tổng Kết Và Bài Tập Tự Luyện
Qua các nội dung đã học, chúng ta đã nắm vững khái niệm vận tốc trung bình, cách tính toán và những ứng dụng thực tiễn của nó. Việc hiểu rõ và áp dụng chính xác công thức tính vận tốc trung bình không chỉ giúp giải quyết các bài toán lý thuyết mà còn hỗ trợ trong nhiều lĩnh vực thực tế.
Để củng cố kiến thức, dưới đây là một số bài tập tự luyện mà bạn có thể thực hiện:
- Bài tập 1: Một chiếc xe di chuyển từ thành phố A đến thành phố B, quãng đường là 120 km, với vận tốc trung bình 60 km/h. Tính thời gian xe di chuyển từ A đến B.
- Bài tập 2: Một người đi bộ trên một con đường thẳng. Quãng đường đi trong 2 giờ đầu là 6 km, sau đó người này nghỉ ngơi 30 phút rồi tiếp tục đi thêm 4 km trong 1 giờ. Tính vận tốc trung bình của người đó trên toàn bộ quãng đường.
- Bài tập 3: Một tàu hỏa di chuyển từ ga X đến ga Y với vận tốc trung bình là 80 km/h trong 3 giờ. Sau đó, tàu dừng lại 20 phút tại ga Y và tiếp tục di chuyển đến ga Z với vận tốc trung bình là 90 km/h trong 2 giờ. Tính vận tốc trung bình của tàu trên cả hành trình từ X đến Z.
Hãy cố gắng giải các bài tập trên và đối chiếu với kết quả để kiểm tra mức độ hiểu bài của bạn. Việc luyện tập đều đặn sẽ giúp bạn nắm vững hơn các khái niệm và công thức đã học.