Công Thức Tính Vận Tốc Truyền Âm: Hướng Dẫn Chi Tiết Và Ứng Dụng Thực Tế

Vận tốc truyền âm là tốc độ lan truyền của sóng âm trong một môi trường cụ thể. Tốc độ này phụ thuộc vào tính chất của môi trường và có thể được tính toán bằng các công thức khác nhau.

1. Công Thức Tính Vận Tốc Truyền Âm Trong Không Khí

Trong không khí ở nhiệt độ \(T\) (đo bằng độ C), vận tốc âm thanh \(v\) có thể được tính bằng công thức:

\[
v = 331.3 + (0.6 \cdot T)
\]

• Ở nhiệt độ 0°C, vận tốc âm thanh là khoảng 331.3 m/s.
• Mỗi độ tăng thêm của nhiệt độ sẽ làm tăng vận tốc âm thanh thêm 0.6 m/s.

2. Công Thức Tính Vận Tốc Truyền Âm Trong Các Môi Trường Khác

Vận tốc âm thanh cũng phụ thuộc vào tính chất của các môi trường khác như nước, thép. Công thức tổng quát để tính vận tốc âm thanh trong một môi trường bất kỳ có dạng:

\[
v = \sqrt{\frac{B}{\rho}}
\]

• \(B\): Mô đun đàn hồi của môi trường (đơn vị Pa).
• \(\rho\): Mật độ của môi trường (đơn vị kg/m³).

Các giá trị vận tốc điển hình:

• Trong nước: khoảng 1500 m/s.
• Trong thép: khoảng 5000 m/s.

3. Công Thức Tính Vận Tốc Truyền Sóng Điện Từ

Vận tốc của sóng điện từ (ví dụ như ánh sáng) được tính theo công thức:

\[
v = \lambda \cdot f
\]

• \(\lambda\): Bước sóng (đơn vị mét).
• \(f\): Tần số (đơn vị Hz).

4. Ứng Dụng Thực Tế Của Vận Tốc Âm Thanh

Vận tốc âm thanh có nhiều ứng dụng thực tiễn trong đời sống và công nghệ:

• Trong y học: Sử dụng trong kỹ thuật siêu âm để tạo hình ảnh bên trong cơ thể.
• Trong hàng không: Xác định số Mach của máy bay, là tỷ lệ giữa vận tốc máy bay và vận tốc âm thanh.
• Trong công nghiệp: Kiểm tra kết cấu vật liệu bằng sóng siêu âm để phát hiện các khuyết tật.

Vận tốc truyền âm, hay tốc độ âm thanh, là tốc độ mà sóng âm di chuyển qua một môi trường. Tốc độ này thay đổi tùy thuộc vào môi trường mà âm thanh truyền qua, như không khí, nước, hay kim loại. Trong không khí, vận tốc âm thanh phụ thuộc chủ yếu vào nhiệt độ và có thể được ước tính bằng công thức:

Trong đó:

• \(c\) là vận tốc âm thanh (m/s)
• \(331.3 \, m/s\) là tốc độ âm thanh trong không khí ở 0°C
• \(\vartheta\) là nhiệt độ không khí (°C)

Tốc độ truyền âm trong chất lỏng và chất rắn thường cao hơn nhiều so với trong không khí. Ví dụ, vận tốc âm thanh trong nước ở nhiệt độ 20°C là khoảng 1481 m/s, trong khi trong một số loại kim loại như thép, vận tốc âm thanh có thể đạt tới 5000 m/s. Điều này là do mật độ và tính đàn hồi của các môi trường khác nhau.

Hiểu biết về vận tốc truyền âm là rất quan trọng trong nhiều lĩnh vực như y học (siêu âm), công nghệ âm thanh, và hàng không. Việc xác định chính xác vận tốc âm thanh giúp cải thiện các công nghệ hiện đại như sonar, radar và các thiết bị đo lường khoa học.

Vận tốc truyền âm trong không khí phụ thuộc vào nhiều yếu tố, trong đó nhiệt độ là yếu tố quan trọng nhất. Công thức tính vận tốc truyền âm trong không khí theo nhiệt độ được xác định như sau:

Công thức:

\[v = 331,3 + 0,6 \cdot \vartheta\]

Trong đó:

• v: Vận tốc truyền âm trong không khí (m/s).
• 331,3: Vận tốc âm thanh trong không khí ở 0°C (m/s).
• 0,6: Hệ số tăng của vận tốc âm thanh khi nhiệt độ tăng 1°C (m/s/°C).
• \(\vartheta\): Nhiệt độ của không khí (°C).

2.1. Công Thức Cơ Bản

Công thức cơ bản để tính vận tốc truyền âm trong không khí là:

\[v = 331,3 + 0,6 \cdot \vartheta\]

Ví dụ, ở nhiệt độ 20°C, vận tốc truyền âm được tính như sau:

\[v = 331,3 + 0,6 \cdot 20 = 343 \, m/s\]

2.2. Ảnh Hưởng Của Nhiệt Độ

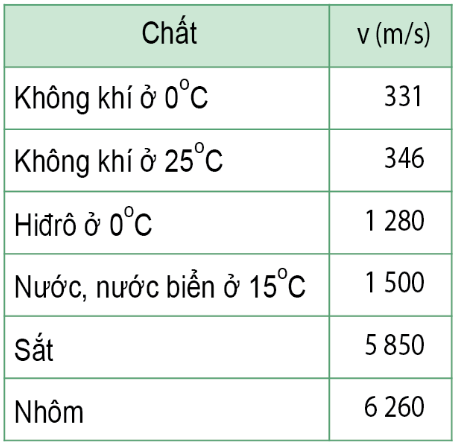
Nhiệt độ không khí ảnh hưởng lớn đến vận tốc truyền âm. Khi nhiệt độ tăng, các phân tử khí di chuyển nhanh hơn, giúp âm thanh truyền đi nhanh hơn. Đối với mỗi 1°C tăng thêm, vận tốc âm thanh tăng khoảng 0,6 m/s. Ví dụ, vận tốc âm thanh ở:

• 0°C: 331,3 m/s
• 15°C: 340 m/s
• 20°C: 343 m/s
• 25°C: 346 m/s

2.3. Ảnh Hưởng Của Độ Ẩm Và Áp Suất

Độ ẩm và áp suất không khí cũng ảnh hưởng đến vận tốc truyền âm, nhưng ít hơn so với nhiệt độ. Không khí ẩm nhẹ hơn không khí khô, làm tăng vận tốc truyền âm. Tuy nhiên, đối với điều kiện khí lý tưởng, vận tốc âm thanh trong không khí không phụ thuộc vào áp suất.

Một số yếu tố ảnh hưởng khác đến vận tốc truyền âm gồm:

• Thành phần không khí (hàm lượng các loại khí khác nhau).
• Độ ẩm của không khí (vận tốc âm tăng trong không khí ẩm).
• Các yếu tố khác như tạp chất trong không khí và cấu trúc của môi trường truyền âm.

Như vậy, vận tốc truyền âm trong không khí phụ thuộc chủ yếu vào nhiệt độ, đồng thời cũng chịu ảnh hưởng bởi độ ẩm và các yếu tố môi trường khác.

Vận tốc truyền âm phụ thuộc vào môi trường mà sóng âm di chuyển qua. Mỗi môi trường có những đặc tính riêng biệt, ảnh hưởng đến tốc độ truyền âm. Dưới đây là các công thức tính vận tốc truyền âm trong một số môi trường phổ biến:

3.1. Vận Tốc Truyền Âm Trong Nước

Vận tốc truyền âm trong nước lớn hơn trong không khí do mật độ phân tử của nước cao hơn. Công thức tính vận tốc âm thanh trong nước có thể biểu diễn như sau:

\[
v_{\text{nước}} = \sqrt{\frac{K}{\rho}}
\]

Trong đó:

• \(v_{\text{nước}}\) là vận tốc truyền âm trong nước.
• \(K\) là hệ số nén của nước (đơn vị: Pascal).
• \(\rho\) là khối lượng riêng của nước (đơn vị: kg/m³).

Ví dụ, vận tốc truyền âm trong nước ngọt ở điều kiện tiêu chuẩn (25°C) là khoảng 1480 m/s.

3.2. Vận Tốc Truyền Âm Trong Các Loại Kim Loại

Âm thanh truyền qua các vật liệu rắn như kim loại với tốc độ rất cao. Điều này là do các phân tử trong kim loại liên kết rất chặt chẽ. Công thức tính vận tốc truyền âm trong kim loại là:

\[
v_{\text{kim loại}} = \sqrt{\frac{E}{\rho}}
\]

Trong đó:

• \(v_{\text{kim loại}}\) là vận tốc truyền âm trong kim loại.
• \(E\) là mô đun đàn hồi của kim loại (đơn vị: Pascal).
• \(\rho\) là khối lượng riêng của kim loại (đơn vị: kg/m³).

Ví dụ, vận tốc truyền âm trong thép là khoảng 5960 m/s, trong khi đó, trong nhôm là khoảng 6420 m/s.

3.3. Vận Tốc Truyền Âm Trong Môi Trường Chân Không

Trong môi trường chân không, không có phân tử vật chất nào để truyền sóng âm, do đó vận tốc truyền âm bằng 0. Âm thanh không thể di chuyển qua chân không.

Điều này khác biệt hoàn toàn so với các môi trường vật chất như khí, lỏng hoặc rắn, nơi mà các hạt phân tử có thể dao động và truyền năng lượng âm thanh từ điểm này đến điểm khác.

Như vậy, tùy vào từng môi trường cụ thể mà vận tốc truyền âm sẽ khác nhau, và công thức tính toán cũng được điều chỉnh để phản ánh các yếu tố vật lý của môi trường đó.

Công thức tính vận tốc của sóng điện từ là một trong những công thức cơ bản trong vật lý, đặc biệt là trong lĩnh vực điện từ học. Vận tốc sóng điện từ trong chân không được xác định bởi hai hằng số vật lý cơ bản: độ từ thẩm \(\mu_0\) và hằng số điện môi \(\epsilon_0\).

Công thức tổng quát tính vận tốc sóng điện từ trong chân không được viết như sau:

Trong đó:

• \(\mu_0\) là độ từ thẩm của chân không, có giá trị xấp xỉ \(4\pi \times 10^{-7} \, \text{H/m}\).
• \(\epsilon_0\) là hằng số điện môi của chân không, có giá trị xấp xỉ \(8.854 \times 10^{-12} \, \text{F/m}\).

Giá trị của \(v\) khi tính toán sẽ cho ra kết quả đúng bằng tốc độ ánh sáng trong chân không:

Công thức này cho thấy vận tốc sóng điện từ chỉ phụ thuộc vào các hằng số vật lý của môi trường mà nó truyền qua. Đối với sóng điện từ truyền trong các môi trường khác, công thức sẽ thay đổi tương ứng với các giá trị của \(\mu\) và \(\epsilon\) trong môi trường đó.

Một phân tích kỹ hơn về công thức này sẽ đưa chúng ta đến với các phương trình Maxwell, từ đó giải thích rõ ràng về mối quan hệ giữa điện trường và từ trường trong sóng điện từ. Theo Maxwell, sự biến đổi của điện trường sẽ sinh ra từ trường và ngược lại, tạo thành một chu kỳ khép kín, cho phép sóng điện từ lan truyền trong không gian mà không cần môi trường vật chất.

Công thức vận tốc sóng điện từ cũng có thể được liên kết với bước sóng \(\lambda\) và tần số \(f\) của sóng:

Điều này có nghĩa là với một tần số cố định, bước sóng càng lớn thì vận tốc truyền sóng càng lớn. Điều này giải thích lý do tại sao sóng điện từ trong môi trường khác nhau sẽ có các bước sóng và vận tốc khác nhau.

Vận tốc truyền âm trong các môi trường khác nhau có thể bị ảnh hưởng bởi nhiều yếu tố, bao gồm nhiệt độ, độ ẩm và áp suất. Các yếu tố này có thể làm thay đổi tốc độ lan truyền của âm thanh, từ đó ảnh hưởng đến chất lượng và độ chính xác của các phép đo hoặc ứng dụng thực tế.

5.1. Ảnh Hưởng Của Nhiệt Độ

Nhiệt độ là một trong những yếu tố chính ảnh hưởng đến vận tốc truyền âm. Khi nhiệt độ tăng, các phân tử trong môi trường di chuyển nhanh hơn, làm tăng tốc độ lan truyền của âm thanh. Công thức liên quan đến ảnh hưởng của nhiệt độ lên vận tốc âm thanh trong không khí có thể được biểu diễn như sau:

\[
v = v_0 + (0.6 \times T)
\]

Trong đó:

• v: Vận tốc âm thanh ở nhiệt độ \( T \) (°C)
• v_0: Vận tốc âm thanh ở 0°C, thường là 331.3 m/s
• T: Nhiệt độ của môi trường (°C)

5.2. Ảnh Hưởng Của Độ Ẩm

Độ ẩm cũng là một yếu tố quan trọng ảnh hưởng đến vận tốc truyền âm. Khi độ ẩm tăng, mật độ của không khí giảm, làm cho vận tốc âm thanh tăng lên. Điều này là do không khí ẩm nhẹ hơn không khí khô, làm giảm sức cản đối với sóng âm.

5.3. Ảnh Hưởng Của Áp Suất

Áp suất của môi trường ảnh hưởng đến vận tốc truyền âm thông qua sự thay đổi trong mật độ không khí. Tuy nhiên, trong điều kiện nhiệt độ cố định, vận tốc truyền âm trong không khí thay đổi không đáng kể với sự thay đổi của áp suất, vì áp suất và mật độ tăng hoặc giảm cùng nhau, dẫn đến vận tốc truyền âm không đổi.

Trong các môi trường khác nhau, các yếu tố này có thể tương tác phức tạp, dẫn đến những thay đổi đáng kể trong vận tốc truyền âm. Việc hiểu rõ các yếu tố ảnh hưởng này là rất quan trọng trong các ứng dụng khoa học và công nghệ liên quan đến âm thanh.

Vận tốc âm thanh không chỉ là một thông số vật lý quan trọng mà còn có rất nhiều ứng dụng thực tế trong đời sống hàng ngày cũng như trong các ngành công nghiệp. Dưới đây là một số ứng dụng tiêu biểu của vận tốc âm thanh:

• Y học: Trong y học, siêu âm là một trong những ứng dụng nổi bật của vận tốc âm thanh. Bằng cách sử dụng sóng siêu âm, các bác sĩ có thể quan sát hình ảnh bên trong cơ thể con người mà không cần phải phẫu thuật. Điều này đặc biệt quan trọng trong việc theo dõi thai nhi, chẩn đoán bệnh tim, và các tình trạng khác.
• Khí tượng học: Vận tốc âm thanh cũng được sử dụng trong việc đo đạc và dự báo thời tiết. Âm thanh của sấm sét có thể được dùng để ước tính khoảng cách của cơn giông dựa trên thời gian giữa ánh sáng của tia chớp và âm thanh của tiếng sét.
• Hàng không: Trong ngành hàng không, việc hiểu rõ vận tốc âm thanh là rất quan trọng. Máy bay siêu thanh có thể bay nhanh hơn tốc độ âm thanh, tạo ra hiện tượng sóng xung kích và tiếng nổ siêu thanh. Việc nghiên cứu và ứng dụng vận tốc âm thanh giúp thiết kế các loại máy bay an toàn và hiệu quả hơn.
• Công nghệ quân sự: Vận tốc âm thanh cũng được áp dụng trong việc phát triển các hệ thống sonar để phát hiện tàu ngầm dưới nước. Hệ thống này hoạt động dựa trên nguyên lý phát ra sóng âm và đo đạc thời gian sóng phản xạ trở lại để xác định vị trí và khoảng cách của các vật thể.
• Âm nhạc: Trong lĩnh vực âm nhạc, vận tốc âm thanh có vai trò quan trọng trong việc điều chỉnh âm thanh và chất lượng âm nhạc. Việc hiểu rõ vận tốc âm thanh giúp các kỹ sư âm thanh điều chỉnh các thiết bị âm thanh để đạt được chất lượng âm thanh tốt nhất trong các buổi hòa nhạc hoặc thu âm.

Như vậy, vận tốc âm thanh không chỉ là một thông số khoa học mà còn có vai trò quan trọng trong nhiều lĩnh vực khác nhau, từ y học đến công nghệ quân sự, và thậm chí là trong âm nhạc.

Dưới đây là một số bài tập và phương pháp thực hành tính toán vận tốc truyền âm, giúp củng cố kiến thức và khả năng áp dụng công thức vào các tình huống thực tế.

• Bài tập 1: Một người đang đứng bên bờ sông và nhìn thấy một tia chớp. Sau khi nhìn thấy tia chớp, anh ta nghe thấy tiếng sấm sau 3 giây. Hãy tính khoảng cách từ nơi xảy ra tia chớp đến vị trí của người đó, biết vận tốc truyền âm trong không khí là \(340 \, \text{m/s}\).

  Hướng dẫn: Sử dụng công thức \( s = v \times t \), trong đó \( s \) là khoảng cách cần tìm, \( v = 340 \, \text{m/s} \) là vận tốc âm thanh, và \( t = 3 \, \text{giây} \).

  Lời giải: \( s = 340 \times 3 = 1020 \, \text{m} \).

• Bài tập 2: Trong một môi trường, cứ 5 giây âm thanh truyền được 7,5 km. Hãy xác định môi trường mà âm thanh đã truyền qua, biết rằng vận tốc âm thanh trong nước là \(1500 \, \text{m/s}\).

  Hướng dẫn: Đầu tiên, tính vận tốc âm thanh dựa trên quãng đường và thời gian, sau đó so sánh với vận tốc âm thanh trong các môi trường khác nhau để xác định môi trường đúng.

  Lời giải: Vận tốc âm thanh \( v = \frac{7500}{5} = 1500 \, \text{m/s} \), điều này cho thấy âm thanh đã truyền qua nước.

• Bài tập 3: Một công nhân gõ mạnh búa xuống đường ray. Sau 1,5 giây, một người đứng cách đó 880 m nghe thấy tiếng búa qua không khí. Tính vận tốc truyền âm trong không khí.

  Hướng dẫn: Áp dụng công thức tính vận tốc \( v = \frac{s}{t} \), trong đó \( s \) là khoảng cách và \( t \) là thời gian.

  Lời giải: \( v = \frac{880}{1.5} = 586.67 \, \text{m/s} \).

• Bài tập 4: Một bạn nhỏ đứng trên bờ, cách một chiếc thuyền đang gõ mạn thuyền 500 m. Nếu vận tốc truyền âm trong không khí là \(340 \, \text{m/s}\), hãy tính thời gian cần để âm thanh truyền tới tai bạn nhỏ.

  Hướng dẫn: Sử dụng công thức \( t = \frac{s}{v} \), trong đó \( s = 500 \, \text{m} \), và \( v = 340 \, \text{m/s} \).

  Lời giải: \( t = \frac{500}{340} \approx 1.47 \, \text{giây} \).

Những bài tập trên giúp bạn nắm vững các khái niệm cơ bản về vận tốc truyền âm cũng như cách ứng dụng công thức vào các tình huống thực tế.