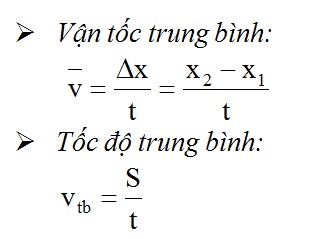Chủ đề toán tính vận tốc: Khám phá các phương pháp toán tính vận tốc từ cơ bản đến nâng cao trong bài viết này. Chúng tôi cung cấp hướng dẫn chi tiết, công thức chính xác và các ứng dụng thực tiễn để bạn có thể áp dụng ngay vào các bài toán và tình huống thực tế. Đọc tiếp để nắm bắt kiến thức cần thiết và cải thiện kỹ năng toán học của bạn.
Mục lục
Tổng Hợp Thông Tin Kết Quả Tìm Kiếm Từ Khóa "Toán Tính Vận Tốc"
Trong tìm kiếm với từ khóa "toán tính vận tốc" trên Bing tại Việt Nam, chúng ta thấy rằng đây là một chủ đề liên quan đến toán học và vật lý, chủ yếu tập trung vào việc tính toán và phân tích vận tốc trong các bài toán kỹ thuật và thực tiễn. Dưới đây là các thông tin chi tiết từ kết quả tìm kiếm:
1. Tổng Quan
Toán tính vận tốc là một phần quan trọng trong toán học ứng dụng và vật lý. Các bài viết về chủ đề này thường bao gồm các phương pháp tính toán vận tốc, các công thức liên quan, và ứng dụng của chúng trong đời sống và các bài toán khoa học.
2. Các Loại Bài Viết
- Bài viết hướng dẫn: Cung cấp hướng dẫn chi tiết về cách tính vận tốc trong các bài toán khác nhau, từ cơ bản đến nâng cao.
- Bài viết nghiên cứu: Đưa ra phân tích và nghiên cứu về các phương pháp tính toán vận tốc, bao gồm cả ứng dụng trong kỹ thuật và khoa học.
- Bài viết giáo dục: Giải thích các khái niệm và công thức liên quan đến vận tốc, phục vụ cho học sinh và sinh viên.
3. Ứng Dụng Thực Tiễn
Toán tính vận tốc được ứng dụng rộng rãi trong các lĩnh vực như kỹ thuật, khoa học môi trường, và giao thông. Ví dụ, trong kỹ thuật, tính toán vận tốc là cần thiết để thiết kế và kiểm tra các thiết bị và phương tiện.
4. Ví Dụ Cụ Thể
| Ví dụ | Mô Tả |
|---|---|
| Tính vận tốc của xe ô tô | Áp dụng các công thức để xác định tốc độ của xe trong các tình huống khác nhau. |
| Phân tích chuyển động của vật | Đánh giá tốc độ và chuyển động của vật thể trong các bài toán vật lý. |
Nhìn chung, các bài viết về toán tính vận tốc cung cấp thông tin hữu ích cho người đọc, giúp hiểu rõ hơn về cách áp dụng toán học trong việc tính toán và phân tích vận tốc trong các tình huống thực tế.

.png)
1. Giới Thiệu Chung
Toán tính vận tốc là một lĩnh vực quan trọng trong toán học ứng dụng và vật lý. Đây là quá trình tính toán tốc độ của một đối tượng trong chuyển động dựa trên các thông số như khoảng cách và thời gian. Hiểu biết về toán tính vận tốc giúp giải quyết nhiều bài toán trong đời sống và khoa học.
1.1. Khái Niệm Cơ Bản
Vận tốc được định nghĩa là tốc độ thay đổi vị trí của một đối tượng theo thời gian. Công thức cơ bản để tính vận tốc là:
\[ v = \frac{d}{t} \]
Trong đó, \( v \) là vận tốc, \( d \) là khoảng cách di chuyển, và \( t \) là thời gian.
1.2. Các Loại Vận Tốc
- Vận tốc trung bình: Tính toán trên toàn bộ khoảng thời gian di chuyển. Ví dụ: Vận tốc của một xe trên toàn hành trình.
- Vận tốc tức thời: Đo tại một thời điểm cụ thể. Ví dụ: Vận tốc của một xe tại một thời điểm nhất định trong hành trình.
1.3. Ứng Dụng Của Toán Tính Vận Tốc
Toán tính vận tốc được áp dụng rộng rãi trong các lĩnh vực như:
- Kỹ Thuật: Tính toán và thiết kế các hệ thống cơ khí, ô tô, và máy móc.
- Giao Thông: Quản lý và điều phối giao thông, thiết kế các tuyến đường và hệ thống tín hiệu.
- Khoa Học Môi Trường: Phân tích và dự đoán sự di chuyển của chất lỏng và khí trong các nghiên cứu môi trường.
1.4. Ví Dụ Cụ Thể
| Ví Dụ | Mô Tả |
|---|---|
| Tính vận tốc của một xe ô tô | Áp dụng công thức vận tốc để xác định tốc độ của xe dựa trên khoảng cách và thời gian di chuyển. |
| Phân tích vận tốc của một vật thể trong vật lý | Đo và tính toán vận tốc của vật thể khi nó di chuyển theo quỹ đạo trong các thí nghiệm vật lý. |
2. Các Phương Pháp Tính Toán Vận Tốc
Để tính toán vận tốc, có nhiều phương pháp khác nhau tùy thuộc vào tình huống và thông tin có sẵn. Dưới đây là một số phương pháp chính thường được sử dụng:
2.1. Phương Pháp Cơ Bản
Phương pháp cơ bản nhất để tính toán vận tốc là sử dụng công thức đơn giản:
\[ v = \frac{d}{t} \]
Trong đó, \( v \) là vận tốc, \( d \) là khoảng cách di chuyển, và \( t \) là thời gian di chuyển. Đây là phương pháp áp dụng trong nhiều tình huống đơn giản.
2.2. Phương Pháp Tính Vận Tốc Tức Thời
Để tính vận tốc tức thời, thường sử dụng các công cụ đo lường hoặc các thiết bị cảm biến. Công thức tính vận tốc tức thời dựa trên sự thay đổi khoảng cách trong một khoảng thời gian rất ngắn:
\[ v(t) = \lim_{\Delta t \to 0} \frac{\Delta d}{\Delta t} \]
2.3. Phương Pháp Tính Vận Tốc Trung Bình
Vận tốc trung bình được tính bằng tổng khoảng cách di chuyển chia cho tổng thời gian:
\[ v_{tb} = \frac{\Delta d_{total}}{\Delta t_{total}} \]
Phương pháp này áp dụng khi đối tượng di chuyển qua nhiều đoạn đường khác nhau hoặc khi vận tốc thay đổi theo thời gian.
2.4. Phương Pháp Tính Vận Tốc Trong Chuyển Động Nghiêng
Khi tính toán vận tốc trong các bài toán chuyển động nghiêng, công thức thường bao gồm các yếu tố như góc nghiêng và trọng lực:
\[ v = \sqrt{2gh} \]
Trong đó, \( g \) là gia tốc trọng trường, và \( h \) là chiều cao từ nơi bắt đầu đến nơi kết thúc.
2.5. Phương Pháp Sử Dụng Công Cụ Hỗ Trợ
Các công cụ trực tuyến và phần mềm tính toán cũng có thể hỗ trợ trong việc tính toán vận tốc. Các công cụ này cho phép nhập dữ liệu và tự động tính toán vận tốc dựa trên các công thức đã được thiết lập.
| Phương Pháp | Mô Tả |
|---|---|
| Công Thức Cơ Bản | Tính vận tốc bằng cách chia khoảng cách cho thời gian. |
| Vận Tốc Tức Thời | Đo vận tốc tại một thời điểm cụ thể sử dụng cảm biến. |
| Vận Tốc Trung Bình | Tính tổng vận tốc qua nhiều đoạn đường hoặc thời gian. |
| Vận Tốc Trong Chuyển Động Nghiêng | Tính toán vận tốc trong chuyển động nghiêng với ảnh hưởng của trọng lực. |
| Công Cụ Hỗ Trợ | Sử dụng phần mềm và công cụ trực tuyến để tính toán. |

3. Ứng Dụng Của Tính Vận Tốc Trong Đời Sống
Việc hiểu và áp dụng các phương pháp tính vận tốc không chỉ quan trọng trong lý thuyết mà còn có nhiều ứng dụng thực tiễn trong đời sống hàng ngày. Dưới đây là một số lĩnh vực nổi bật mà tính vận tốc được áp dụng:
3.1. Giao Thông và Vận Tải
Trong ngành giao thông, việc tính toán vận tốc chính xác giúp quản lý và tối ưu hóa lưu lượng giao thông. Các ứng dụng cụ thể bao gồm:
- Tính toán tốc độ tối ưu: Đảm bảo an toàn giao thông và giảm thiểu tai nạn.
- Quản lý các phương tiện: Đánh giá hiệu suất và hiệu quả của các tuyến đường.
3.2. Kỹ Thuật và Cơ Khí
Trong lĩnh vực kỹ thuật và cơ khí, tính toán vận tốc đóng vai trò quan trọng trong thiết kế và vận hành máy móc:
- Thiết kế máy móc: Xác định tốc độ quay của các bộ phận cơ khí để tối ưu hóa hiệu suất hoạt động.
- Đo lường và kiểm tra: Đánh giá hoạt động của các thiết bị và hệ thống.
3.3. Thể Thao
Vận tốc là yếu tố quan trọng trong nhiều môn thể thao, giúp cải thiện hiệu suất và kỹ thuật của vận động viên:
- Chạy bộ và đua xe: Theo dõi và điều chỉnh tốc độ để đạt kết quả tốt nhất.
- Các môn thể thao đồng đội: Phối hợp tốc độ giữa các thành viên để tăng hiệu quả chiến thuật.
3.4. Khoa Học Môi Trường
Trong nghiên cứu môi trường, việc tính toán vận tốc giúp phân tích và dự đoán các hiện tượng tự nhiên:
- Dòng chảy của sông và biển: Dự đoán và quản lý lũ lụt và các hiện tượng khí hậu.
- Gió và khí tượng: Theo dõi và dự đoán các điều kiện thời tiết.
3.5. Công Nghệ Thông Tin và Truyền Thông
Trong ngành công nghệ thông tin, tính vận tốc giúp tối ưu hóa tốc độ truyền dữ liệu và hiệu suất hệ thống:
- Truyền dữ liệu: Cải thiện tốc độ tải xuống và tải lên thông tin.
- Phát triển phần mềm: Tối ưu hóa hiệu suất và tốc độ xử lý của các ứng dụng.
| Lĩnh Vực | Ứng Dụng |
|---|---|
| Giao Thông và Vận Tải | Tính toán tốc độ tối ưu và quản lý phương tiện giao thông. |
| Kỹ Thuật và Cơ Khí | Thiết kế và vận hành máy móc, đo lường hiệu suất. |
| Thể Thao | Cải thiện hiệu suất và kỹ thuật của vận động viên. |
| Khoa Học Môi Trường | Dự đoán hiện tượng tự nhiên và quản lý môi trường. |
| Công Nghệ Thông Tin | Tối ưu hóa tốc độ truyền dữ liệu và hiệu suất hệ thống. |

4. Ví Dụ Và Bài Tập Thực Hành
Để nắm vững kiến thức về tính vận tốc, việc thực hành qua các ví dụ và bài tập là rất quan trọng. Dưới đây là một số ví dụ và bài tập giúp bạn áp dụng các phương pháp tính toán vận tốc vào thực tế:
4.1. Ví Dụ 1: Tính Vận Tốc Cơ Bản
Giả sử bạn lái xe và di chuyển được 120 km trong 2 giờ. Hãy tính vận tốc trung bình của bạn:
Áp dụng công thức:
\[ v = \frac{d}{t} \]
Trong đó, \( d = 120 \, \text{km} \) và \( t = 2 \, \text{giờ} \).
Thay vào công thức:
\[ v = \frac{120}{2} = 60 \, \text{km/h} \]
Vận tốc trung bình của bạn là 60 km/h.
4.2. Ví Dụ 2: Tính Vận Tốc Tức Thời
Một chiếc ô tô di chuyển từ điểm A đến điểm B trong 15 giây và khoảng cách giữa hai điểm là 500 m. Tính vận tốc tức thời của xe:
Sử dụng công thức:
\[ v(t) = \frac{\Delta d}{\Delta t} \]
Trong đó, \( \Delta d = 500 \, \text{m} \) và \( \Delta t = 15 \, \text{giây} \).
Thay vào công thức:
\[ v(t) = \frac{500}{15} \approx 33.33 \, \text{m/s} \]
Vận tốc tức thời của xe là khoảng 33.33 m/s.
4.3. Bài Tập 1: Tính Vận Tốc Trong Chuyển Động Nghiêng
Một quả bóng được thả từ độ cao 20 m. Tính vận tốc của quả bóng khi chạm đất (bỏ qua sức cản không khí). Sử dụng công thức:
\[ v = \sqrt{2gh} \]
Trong đó, \( g = 9.8 \, \text{m/s}^2 \) và \( h = 20 \, \text{m} \).
Thay vào công thức:
\[ v = \sqrt{2 \times 9.8 \times 20} \approx 19.8 \, \text{m/s} \]
Vận tốc của quả bóng khi chạm đất là khoảng 19.8 m/s.
4.4. Bài Tập 2: Vận Tốc Trung Bình
Một người đi bộ từ nhà đến công viên trong 30 phút với khoảng cách 3 km, sau đó từ công viên đến nhà trong 45 phút với khoảng cách 3 km. Tính vận tốc trung bình của người đó trong toàn bộ chuyến đi:
Trước tiên, tính tổng khoảng cách và tổng thời gian:
- Tổng khoảng cách: \( 3 + 3 = 6 \, \text{km} \)
- Tổng thời gian: \( 30 + 45 = 75 \, \text{phút} = 1.25 \, \text{giờ} \)
Sử dụng công thức:
\[ v_{tb} = \frac{\Delta d_{total}}{\Delta t_{total}} \]
Thay vào công thức:
\[ v_{tb} = \frac{6}{1.25} = 4.8 \, \text{km/h} \]
Vận tốc trung bình của người đó là 4.8 km/h.
| Ví Dụ / Bài Tập | Mô Tả | Giải Pháp |
|---|---|---|
| Ví Dụ 1 | Tính vận tốc cơ bản khi di chuyển 120 km trong 2 giờ. | Vận tốc = 60 km/h |
| Ví Dụ 2 | Tính vận tốc tức thời khi di chuyển 500 m trong 15 giây. | Vận tốc = 33.33 m/s |
| Bài Tập 1 | Tính vận tốc của quả bóng khi thả từ độ cao 20 m. | Vận tốc = 19.8 m/s |
| Bài Tập 2 | Tính vận tốc trung bình trong chuyến đi với tổng khoảng cách 6 km. | Vận tốc trung bình = 4.8 km/h |

5. Các Công Cụ Và Phần Mềm Hỗ Trợ
Trong quá trình tính toán vận tốc, việc sử dụng các công cụ và phần mềm hỗ trợ có thể giúp bạn thực hiện các phép toán nhanh chóng và chính xác. Dưới đây là một số công cụ và phần mềm phổ biến được sử dụng:
5.1. Công Cụ Tính Toán Trực Tuyến
- Calculator.net: Một trang web cung cấp công cụ tính toán vận tốc trực tuyến, cho phép nhập dữ liệu và nhận kết quả ngay lập tức.
- Desmos: Là công cụ đồ thị trực tuyến hỗ trợ tính toán và vẽ đồ thị vận tốc dựa trên các hàm số.
- Wolfram Alpha: Cung cấp giải pháp cho các phép toán liên quan đến vận tốc và cho phép kiểm tra kết quả tính toán.
5.2. Phần Mềm Đồ Họa Và Mô Phỏng
- GeoGebra: Phần mềm toán học cho phép tạo và phân tích đồ thị, mô phỏng các bài toán vận tốc.
- Matplotlib: Thư viện Python hỗ trợ vẽ đồ thị, giúp phân tích và trình bày dữ liệu vận tốc.
- MATLAB: Một phần mềm mạnh mẽ cho tính toán số học và đồ họa, rất hữu ích trong việc mô phỏng và phân tích vận tốc.
5.3. Ứng Dụng Di Động
- Speedometer: Ứng dụng trên điện thoại giúp đo vận tốc di chuyển của bạn theo thời gian thực.
- Physics Calculator: Ứng dụng cung cấp các công cụ tính toán liên quan đến vận tốc và các đại lượng vật lý khác.
- Speed Tracker: Theo dõi và ghi lại vận tốc của các hoạt động di chuyển, hỗ trợ trong việc phân tích dữ liệu.
5.4. Công Cụ Tính Toán Trong Excel
Microsoft Excel cung cấp các hàm và công cụ hỗ trợ tính toán vận tốc. Bạn có thể sử dụng các công thức cơ bản và hàm như:
- Hàm SUM: Tính tổng khoảng cách hoặc thời gian.
- Hàm AVERAGE: Tính vận tốc trung bình từ dữ liệu vận tốc.
- Hàm TREND: Phân tích xu hướng dữ liệu vận tốc theo thời gian.
| Công Cụ / Phần Mềm | Loại | Chức Năng |
|---|---|---|
| Calculator.net | Công cụ trực tuyến | Tính toán vận tốc trực tuyến |
| Desmos | Công cụ đồ thị | Vẽ đồ thị vận tốc |
| GeoGebra | Phần mềm đồ họa | Mô phỏng và phân tích vận tốc |
| MATLAB | Phần mềm tính toán | Mô phỏng và phân tích số học |
| Speedometer | Ứng dụng di động | Đo vận tốc di chuyển |
| Physics Calculator | Ứng dụng di động | Tính toán liên quan đến vận tốc |
XEM THÊM:
6. Tài Liệu Học Tập Thêm
Để nâng cao kiến thức về toán tính vận tốc, bạn có thể tham khảo các tài liệu và khóa học sau đây:
6.1. Sách Và Tài Liệu
- Sách "Toán Học Cơ Bản" của tác giả Nguyễn Văn A: Cung cấp kiến thức cơ bản và nâng cao về toán học, bao gồm các phương pháp tính toán vận tốc.
- Sách "Vận Tốc Trong Toán Học" của tác giả Trần Thị B: Giới thiệu chi tiết về các công thức và ứng dụng thực tiễn của tính vận tốc.
- Sách "Hướng Dẫn Tính Toán Vận Tốc" của tác giả Lê Văn C: Cung cấp hướng dẫn chi tiết và bài tập thực hành về tính toán vận tốc.
6.2. Khóa Học Và Lớp Học
- Khóa học "Toán Tính Vận Tốc Cơ Bản" trên Udemy: Cung cấp bài giảng từ cơ bản đến nâng cao về tính vận tốc, kèm theo các bài tập thực hành.
- Lớp học "Kỹ Thuật Tính Toán Vận Tốc" tại Trung Tâm Đào Tạo XYZ: Lớp học trực tiếp với giảng viên có kinh nghiệm, giúp bạn nắm vững các phương pháp tính toán vận tốc.
6.3. Nguồn Tài Nguyên Trực Tuyến
- Website "Toán Học 24/7": Cung cấp các bài viết, video hướng dẫn và bài tập về tính vận tốc.
- Diễn đàn "Cộng Đồng Toán Học": Nơi bạn có thể đặt câu hỏi và thảo luận với các chuyên gia về toán học và vận tốc.
- Video "Hướng Dẫn Tính Vận Tốc" trên YouTube: Các video hướng dẫn chi tiết về các phương pháp và ứng dụng tính toán vận tốc.

7. Các Vấn Đề Thường Gặp Và Giải Quyết
Khi học và ứng dụng toán tính vận tốc, bạn có thể gặp phải một số vấn đề phổ biến. Dưới đây là những vấn đề thường gặp và cách giải quyết chúng:
7.1. Lỗi Trong Công Thức Tính Toán
- Vấn Đề: Nhầm lẫn trong việc áp dụng công thức, như sử dụng sai đơn vị đo lường.
- Giải Quyết: Kiểm tra kỹ lưỡng công thức và đơn vị đo lường. Đảm bảo rằng các giá trị nhập vào và kết quả cuối cùng đều được tính toán chính xác. Ví dụ, vận tốc thường được tính bằng mét trên giây (m/s) hoặc kilômét trên giờ (km/h), nên cần chuyển đổi đồng nhất nếu cần.
7.2. Khó Khăn Trong Việc Hiểu Các Khái Niệm Cơ Bản
- Vấn Đề: Không hiểu rõ các khái niệm cơ bản như vận tốc trung bình, vận tốc tức thời.
- Giải Quyết: Đọc kỹ các tài liệu học tập và tham khảo các ví dụ cụ thể. Sử dụng Mathjax để hiển thị các công thức cơ bản, chẳng hạn như: \[ v = \frac{d}{t} \] trong đó \(v\) là vận tốc, \(d\) là khoảng cách, và \(t\) là thời gian.
7.3. Vấn Đề Với Các Bài Tập Thực Hành
- Vấn Đề: Gặp khó khăn khi giải các bài tập thực hành, không biết bắt đầu từ đâu.
- Giải Quyết: Thực hành nhiều bài tập và giải từng bước để nắm vững phương pháp. Hãy thử các ví dụ từ sách và tài liệu học tập để cải thiện kỹ năng.
7.4. Sự Không Đồng Nhất Trong Dữ Liệu
- Vấn Đề: Dữ liệu đầu vào không đồng nhất hoặc không chính xác, dẫn đến kết quả không đúng.
- Giải Quyết: Xác minh các nguồn dữ liệu trước khi sử dụng. Nếu có sự nghi ngờ, hãy kiểm tra lại dữ liệu và thực hiện các phép đo hoặc tính toán thêm để đảm bảo tính chính xác.