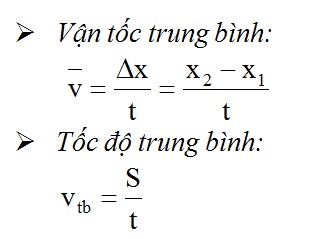Chủ đề bài toán tính vận tốc trung bình lớp 5: Khám phá bài toán tính vận tốc trung bình lớp 5 với hướng dẫn chi tiết và ví dụ thực tế giúp học sinh dễ dàng nắm bắt. Bài viết này cung cấp công thức cơ bản, các bước giải quyết bài toán, và ứng dụng thực tế để học sinh có thể áp dụng kiến thức vào các tình huống hàng ngày.
Mục lục
Bài Toán Tính Vận Tốc Trung Bình Lớp 5
Bài toán tính vận tốc trung bình là một phần quan trọng trong chương trình học của lớp 5. Dưới đây là một số thông tin chi tiết về chủ đề này:
Các Khái Niệm Cơ Bản
- Vận Tốc Trung Bình: Vận tốc trung bình được tính bằng cách chia tổng quãng đường di chuyển cho tổng thời gian di chuyển. Công thức tính vận tốc trung bình là: \[ v = \frac{d}{t} \] Trong đó, \( v \) là vận tốc trung bình, \( d \) là quãng đường, và \( t \) là thời gian.
- Ví Dụ: Nếu một xe di chuyển 120 km trong 2 giờ, vận tốc trung bình của xe là: \[ v = \frac{120 \text{ km}}{2 \text{ giờ}} = 60 \text{ km/h} \]
Phương Pháp Giải Bài Toán
- Xác định tổng quãng đường di chuyển.
- Xác định tổng thời gian di chuyển.
- Áp dụng công thức tính vận tốc trung bình để tìm kết quả.
Ứng Dụng Thực Tế
Bài toán tính vận tốc trung bình giúp học sinh hiểu được cách áp dụng các khái niệm toán học vào các tình huống thực tế, như tính toán thời gian di chuyển của các phương tiện giao thông.
Ví Dụ Thực Tế
| Quãng Đường (km) | Thời Gian (giờ) | Vận Tốc Trung Bình (km/h) |
|---|---|---|
| 150 | 3 | \[ \frac{150}{3} = 50 \] |
| 200 | 4 | \[ \frac{200}{4} = 50 \] |

.png)
Giới Thiệu Chung
Bài toán tính vận tốc trung bình là một phần quan trọng trong chương trình toán lớp 5. Nó giúp học sinh làm quen với việc tính toán và ứng dụng kiến thức toán học vào các tình huống thực tế. Dưới đây là một số thông tin cơ bản về chủ đề này:
Khái Niệm Cơ Bản
- Vận Tốc Trung Bình: Vận tốc trung bình được xác định bằng cách chia tổng quãng đường di chuyển cho tổng thời gian di chuyển. Công thức tính vận tốc trung bình là: \[ v = \frac{d}{t} \] Trong đó, \( v \) là vận tốc trung bình, \( d \) là quãng đường, và \( t \) là thời gian.
- Ý Nghĩa: Hiểu và áp dụng công thức này giúp học sinh giải quyết các bài toán liên quan đến chuyển động và tốc độ trong cuộc sống hàng ngày.
Ứng Dụng Trong Giảng Dạy
Bài toán tính vận tốc trung bình không chỉ giúp học sinh củng cố kiến thức toán học mà còn giúp rèn luyện kỹ năng giải quyết vấn đề và tư duy logic. Thông qua các bài tập và ví dụ, học sinh học cách phân tích và xử lý thông tin để tìm ra kết quả chính xác.
Ví Dụ Minh Họa
| Quãng Đường (km) | Thời Gian (giờ) | Vận Tốc Trung Bình (km/h) |
|---|---|---|
| 60 | 1.5 | \[ \frac{60}{1.5} = 40 \] |
| 90 | 3 | \[ \frac{90}{3} = 30 \] |
Các Loại Bài Toán
Các bài toán tính vận tốc trung bình lớp 5 có thể được chia thành nhiều loại khác nhau, tùy thuộc vào nội dung và mục đích của bài toán. Dưới đây là các loại bài toán phổ biến trong chương trình học:
Bài Toán Cơ Bản
- Bài Toán Tính Vận Tốc Trung Bình Đơn Giản: Những bài toán này yêu cầu học sinh tính vận tốc trung bình khi biết quãng đường và thời gian. Ví dụ: Nếu một xe di chuyển 100 km trong 2 giờ, vận tốc trung bình là: \[ v = \frac{100}{2} = 50 \text{ km/h} \]
- Bài Toán Tính Quãng Đường Hoặc Thời Gian: Khi biết vận tốc và một trong hai yếu tố còn lại (quãng đường hoặc thời gian), học sinh cần tính toán yếu tố còn lại. Ví dụ: Nếu vận tốc là 60 km/h và thời gian là 3 giờ, quãng đường sẽ là: \[ d = v \times t = 60 \times 3 = 180 \text{ km} \]
Bài Toán Ứng Dụng Thực Tế
- Bài Toán Vận Tốc Trong Cuộc Sống: Các bài toán mô phỏng tình huống thực tế như tính toán thời gian di chuyển của xe, tàu, hay máy bay. Ví dụ: Một chuyến tàu di chuyển 250 km trong 5 giờ, vận tốc trung bình của tàu là: \[ v = \frac{250}{5} = 50 \text{ km/h} \]
- Bài Toán So Sánh Vận Tốc: Học sinh so sánh vận tốc của các phương tiện khác nhau hoặc so sánh vận tốc trong các khoảng thời gian khác nhau. Ví dụ: So sánh vận tốc của xe đạp và xe máy trên cùng một quãng đường.
Bài Toán Kết Hợp Với Các Khái Niệm Khác
- Bài Toán Kết Hợp Với Tốc Độ Trung Bình: Những bài toán yêu cầu học sinh áp dụng kiến thức về tốc độ và vận tốc trong các tình huống phức tạp hơn. Ví dụ: Tính vận tốc trung bình khi quãng đường thay đổi hoặc thời gian di chuyển không đồng đều.
- Bài Toán Vận Tốc Với Các Đơn Vị Khác Nhau: Các bài toán yêu cầu chuyển đổi giữa các đơn vị đo lường như km/h sang m/s hoặc ngược lại.
Ví Dụ Minh Họa
| Loại Bài Toán | Quãng Đường (km) | Thời Gian (giờ) | Vận Tốc Trung Bình (km/h) |
|---|---|---|---|
| Bài Toán Cơ Bản | 120 | 2 | \[ \frac{120}{2} = 60 \] |
| Bài Toán Ứng Dụng Thực Tế | 150 | 3 | \[ \frac{150}{3} = 50 \] |
| Bài Toán Kết Hợp Khái Niệm Khác | 180 | 4.5 | \[ \frac{180}{4.5} = 40 \] |

Phân Tích Chuyên Sâu
Phân tích chuyên sâu các bài toán tính vận tốc trung bình giúp học sinh hiểu rõ hơn về các phương pháp và ứng dụng của chúng. Dưới đây là những điểm quan trọng cần lưu ý:
Giải Thích Chi Tiết Các Bài Toán
Để giải thích chi tiết, hãy chia bài toán thành các phần cơ bản:
- Nhận diện các yếu tố cần thiết: quãng đường và thời gian.
- Áp dụng công thức tính vận tốc trung bình: \[ v = \frac{s}{t} \]
- Giải quyết từng phần bài toán và trình bày kết quả rõ ràng.
So Sánh Các Phương Pháp Giải Quyết
Có nhiều phương pháp giải bài toán tính vận tốc trung bình:
- Phương pháp trực tiếp: Sử dụng công thức tính vận tốc trung bình ngay lập tức.
- Phương pháp phân tích: Chia nhỏ bài toán thành các phần và tính toán từng phần một.
- Phương pháp hình ảnh: Sử dụng đồ thị và hình ảnh để trực quan hóa vấn đề.
Ứng Dụng Thực Tế Và Tình Huống
Vận tốc trung bình không chỉ là một khái niệm toán học mà còn có ứng dụng thực tế:
| Tình Huống | Ứng Dụng |
|---|---|
| Điểm đến xa | Tính thời gian cần thiết để đến nơi dựa trên vận tốc. |
| Giao thông | Xác định tốc độ di chuyển của phương tiện để quản lý thời gian. |

Ôn Tập Và Kiểm Tra
Ôn tập và kiểm tra là phần quan trọng để củng cố kiến thức và đánh giá hiểu biết của học sinh về bài toán tính vận tốc trung bình. Dưới đây là các phần cần chú ý:
Các Bài Tập Ôn Tập
Để ôn tập hiệu quả, hãy làm các bài tập sau:
- Tính vận tốc trung bình khi quãng đường là 120 km và thời gian là 2 giờ.
- Tìm thời gian cần thiết để di chuyển 150 km với vận tốc 50 km/h.
- So sánh vận tốc trung bình của hai chuyến đi với quãng đường và thời gian khác nhau.
Đề Kiểm Tra Và Đáp Án
Dưới đây là một số đề kiểm tra và đáp án để tự đánh giá:
| Đề Bài | Đáp Án |
|---|---|
| Tính vận tốc trung bình của một xe chạy 180 km trong 3 giờ. | \[ v = \frac{180}{3} = 60 \text{ km/h} \] |
| Tìm thời gian cần thiết để đi 200 km với vận tốc 80 km/h. | \[ t = \frac{200}{80} = 2.5 \text{ giờ} \] |
Hướng Dẫn Cải Thiện Kỹ Năng
Để cải thiện kỹ năng, hãy thực hiện các bước sau:
- Thực hành thường xuyên với nhiều bài tập khác nhau.
- Kiểm tra và sửa lỗi sai để hiểu rõ hơn về các vấn đề.
- Tham khảo thêm tài liệu và hướng dẫn trực tuyến để nâng cao kiến thức.

Tài Liệu Tham Khảo
Để hỗ trợ việc học tập và giảng dạy bài toán tính vận tốc trung bình lớp 5, bạn có thể tham khảo các tài liệu sau:
Sách Giáo Khoa
- Sách Giáo Khoa Toán 5 - Nhà xuất bản Giáo dục Việt Nam.
- Sách Bài Tập Toán 5 - Nhà xuất bản Giáo dục Việt Nam.
Trang Web Giáo Dục
- - Cung cấp các bài học và bài tập toán lớp 5.
- - Nơi chia sẻ kiến thức và phương pháp giải toán.
Video Hướng Dẫn
- - Các video hướng dẫn giải bài toán vận tốc trung bình lớp 5.
- - Các bài giảng và bài tập về vận tốc trung bình.