Công Thức Tính Vận Tốc Tức Thời Đạo Hàm: Bí Quyết Chinh Phục Mọi Bài Tập

Vận tốc tức thời là đại lượng đặc trưng cho tốc độ của một vật tại một thời điểm cụ thể. Để tính toán vận tốc tức thời, ta thường sử dụng đạo hàm trong toán học.

1.1. Định Nghĩa

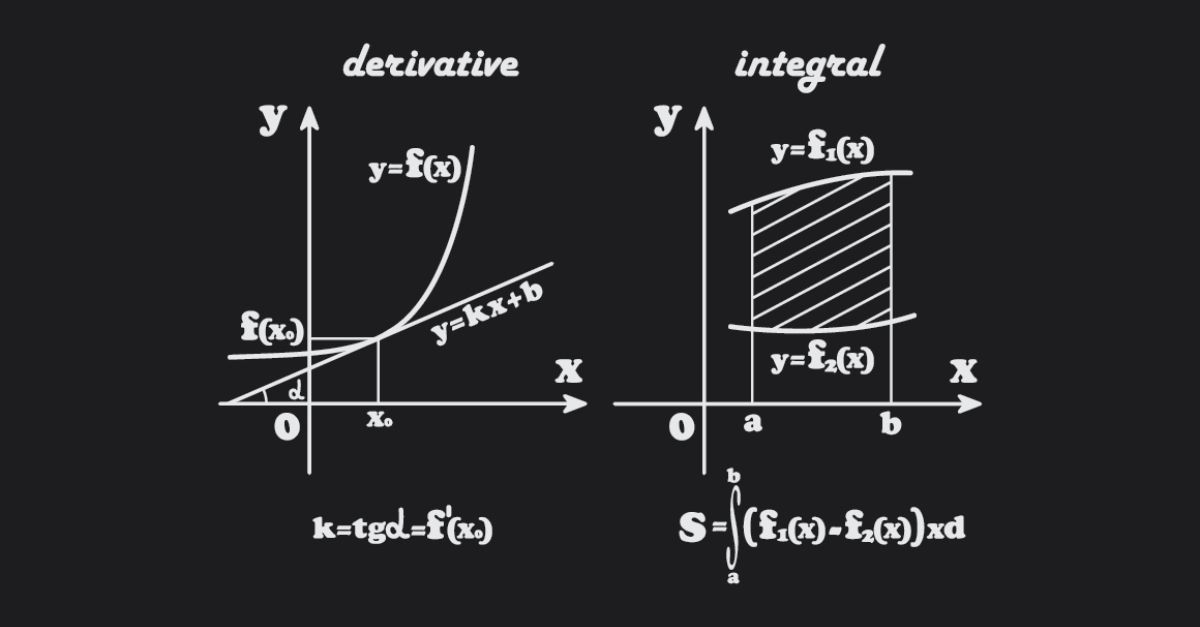
Vận tốc tức thời của một vật tại thời điểm \( t \) được định nghĩa là đạo hàm của hàm vị trí theo thời gian tại thời điểm đó. Nếu \( s(t) \) là hàm mô tả vị trí của vật theo thời gian, thì vận tốc tức thời \( v(t) \) được tính bằng:

\[
v(t) = \frac{ds(t)}{dt}
\]

1.2. Ví Dụ Cụ Thể

Giả sử hàm vị trí của một vật chuyển động là \( s(t) = 5t^2 + 2t \). Để tìm vận tốc tức thời, ta tính đạo hàm của hàm vị trí:

\[
v(t) = \frac{d}{dt}[5t^2 + 2t] = 10t + 2
\]

1.3. Ý Nghĩa Của Vận Tốc Tức Thời

Vận tốc tức thời cho biết tốc độ của vật tại một thời điểm cụ thể, giúp hiểu rõ hơn về chuyển động của vật. Ví dụ, nếu vận tốc tức thời tại \( t = 3 \) giây là:

\[
v(3) = 10 \cdot 3 + 2 = 32 \text{ m/s}
\]

1.4. Ứng Dụng Trong Thực Tế

Trong thực tế, công thức tính vận tốc tức thời được sử dụng trong nhiều lĩnh vực, từ khoa học cơ bản đến kỹ thuật và công nghệ, giúp phân tích và dự đoán chuyển động của các đối tượng.

Vận tốc tức thời là một khái niệm quan trọng trong vật lý, giúp mô tả vận tốc của một vật tại một thời điểm cụ thể. Để hiểu rõ hơn về vận tốc tức thời, ta cần xem xét quá trình chuyển động của vật và tìm hiểu cách thức mà vận tốc này được xác định thông qua đạo hàm.

Giả sử một vật di chuyển dọc theo một đường thẳng với quãng đường được mô tả bởi hàm số \( s(t) \), trong đó \( t \) là thời gian. Vận tốc tức thời tại thời điểm \( t \) chính là đạo hàm của hàm số \( s(t) \) theo thời gian, được ký hiệu là \( v(t) = s'(t) \). Điều này có nghĩa là vận tốc tức thời biểu thị tốc độ thay đổi của quãng đường theo thời gian tại một thời điểm cụ thể.

• Đối với chuyển động thẳng đều: Vận tốc tức thời sẽ không đổi và bằng vận tốc trung bình.
• Đối với chuyển động biến đổi đều: Vận tốc tức thời tại thời điểm \( t \) có thể được tính bằng đạo hàm của hàm chuyển động.

Nhờ vào khái niệm này, ta có thể hiểu rõ hơn về cách thức một vật di chuyển và dự đoán được vị trí, tốc độ của vật tại bất kỳ thời điểm nào trong quá trình chuyển động.

Vận tốc tức thời được xác định bằng cách lấy đạo hàm của quãng đường \( s(t) \) theo thời gian \( t \). Công thức cơ bản để tính vận tốc tức thời là:

Trong đó:

• \( v(t) \): Vận tốc tức thời tại thời điểm \( t \).
• \( s(t) \): Quãng đường mà vật đã di chuyển tính từ thời điểm ban đầu đến thời điểm \( t \).
• \( \frac{ds(t)}{dt} \): Đạo hàm của hàm số quãng đường theo thời gian.

Ví dụ: Giả sử một vật di chuyển theo phương trình \( s(t) = 5t^2 + 3t + 2 \), vận tốc tức thời của vật tại thời điểm \( t \) sẽ là:

Như vậy, vận tốc tức thời phụ thuộc vào thời gian và thay đổi liên tục theo thời gian. Việc nắm vững cách tính vận tốc tức thời bằng đạo hàm giúp chúng ta hiểu rõ hơn về bản chất của chuyển động trong các trường hợp cụ thể.

Vận tốc tức thời là một khái niệm quan trọng trong vật lý và có nhiều ứng dụng thực tiễn trong cuộc sống cũng như trong các lĩnh vực kỹ thuật. Dưới đây là một số ứng dụng cụ thể của vận tốc tức thời:

• Trong giao thông: Vận tốc tức thời giúp theo dõi và điều chỉnh tốc độ của phương tiện giao thông như ô tô, tàu hỏa, và máy bay, đảm bảo an toàn và hiệu quả trong vận hành.
• Trong thể thao: Vận tốc tức thời được sử dụng để đánh giá hiệu suất của các vận động viên, đặc biệt trong các môn đua xe, chạy đua, và bơi lội, nơi mà từng khoảnh khắc có thể quyết định chiến thắng.
• Trong sản xuất: Việc đo lường vận tốc tức thời của các bộ phận máy móc giúp đảm bảo quá trình sản xuất diễn ra ổn định và tránh các lỗi kỹ thuật do sự thay đổi đột ngột trong tốc độ hoạt động.
• Trong nghiên cứu khoa học: Vận tốc tức thời là công cụ cần thiết để phân tích chuyển động của các đối tượng trong nghiên cứu, từ vi mô như hạt phân tử cho đến vĩ mô như hành tinh trong vũ trụ.
• Trong cơ học: Ứng dụng của đạo hàm trong tính vận tốc tức thời giúp xác định chính xác vận tốc của vật tại một thời điểm cụ thể, từ đó giúp phân tích và dự đoán chuyển động trong các hệ thống cơ học phức tạp.

Công thức tính vận tốc tức thời sử dụng đạo hàm được biểu diễn bằng:

\[v(t) = \lim_{\Delta t \to 0} \frac{\Delta s}{\Delta t} = \frac{ds}{dt}\]

Trong đó:

• \(v(t)\) là vận tốc tức thời tại thời điểm \(t\).
• \(\Delta s\) là sự thay đổi vị trí trong khoảng thời gian \(\Delta t\).
• \(\frac{ds}{dt}\) là đạo hàm của vị trí theo thời gian, biểu thị vận tốc tức thời.

Trong quá trình học tập và thực hành các bài tập về vận tốc tức thời, việc áp dụng công thức đạo hàm là rất quan trọng. Dưới đây là các bước cụ thể để giải các dạng bài tập liên quan:

1. Xác định phương trình chuyển động

   Trước hết, hãy xác định phương trình chuyển động của vật, thường được biểu diễn dưới dạng \( s(t) \), trong đó \( s \) là quãng đường và \( t \) là thời gian.

2. Tìm đạo hàm của phương trình

   Tiếp theo, tính đạo hàm của phương trình chuyển động để tìm ra vận tốc tức thời. Công thức chung là:

   \[
   v(t) = s'(t)
   \]

   Đạo hàm này cho ta biết vận tốc của vật tại một thời điểm \( t \) bất kỳ.

3. Áp dụng đạo hàm vào bài toán cụ thể

   Sau khi có được công thức vận tốc, hãy thay giá trị cụ thể của \( t \) vào để tính vận tốc tức thời tại thời điểm đó. Ví dụ:

   • Cho phương trình chuyển động \( s(t) = t^2 + 4t + 5 \), ta có:
   • Đạo hàm: \( v(t) = s'(t) = 2t + 4 \)
   • Vận tốc tại thời điểm \( t = 3 \) là \( v(3) = 2(3) + 4 = 10 \) m/s.
4. Kiểm tra và đối chiếu kết quả

   Cuối cùng, sau khi tính toán, hãy kiểm tra lại kết quả để đảm bảo tính chính xác và hợp lý. Điều này rất quan trọng trong các bài toán có nhiều bước phức tạp.

Với các bước trên, bạn có thể giải quyết hầu hết các dạng bài tập liên quan đến vận tốc tức thời một cách dễ dàng và chính xác.

Vận tốc tức thời là một khái niệm quan trọng trong vật lý, đặc biệt khi sử dụng đạo hàm để tính toán. Dưới đây là một số lưu ý cần thiết để đảm bảo độ chính xác và tránh sai sót khi tính toán vận tốc tức thời:

• Hiểu rõ khái niệm đạo hàm: Đạo hàm của hàm số \(x(t)\) theo thời gian \(t\) chính là vận tốc tức thời tại thời điểm đó. Điều này đòi hỏi bạn phải hiểu rõ cách áp dụng đạo hàm vào các hàm số cụ thể.
• Xác định đúng hàm số cần đạo hàm: Khi tính vận tốc tức thời, bạn cần phải xác định đúng hàm số chuyển động của đối tượng theo thời gian, có thể là \(x(t)\), \(s(t)\), hoặc bất kỳ biến thể nào khác.
• Làm quen với các công thức đạo hàm cơ bản: Để tính đạo hàm chính xác, cần thuộc các công thức đạo hàm cơ bản như:
  • \((f(x) + g(x))' = f'(x) + g'(x)\)
  • \((f(x) \cdot g(x))' = f'(x) \cdot g(x) + f(x) \cdot g'(x)\)
  • \((\frac{f(x)}{g(x)})' = \frac{f'(x) \cdot g(x) - f(x) \cdot g'(x)}{(g(x))^2}\)
• Chú ý đến đơn vị đo: Khi tính toán vận tốc tức thời, đơn vị của kết quả thường là mét/giây (m/s). Đảm bảo rằng các đơn vị đo trong bài toán của bạn đã được chuyển đổi phù hợp trước khi áp dụng công thức.
• Kiểm tra kết quả cuối cùng: Sau khi tính toán, hãy kiểm tra lại kết quả để đảm bảo rằng đạo hàm và vận tốc tức thời đã được tính chính xác. Điều này bao gồm kiểm tra dấu của đạo hàm và so sánh với các giá trị thực tế nếu có thể.
• Sử dụng phần mềm hỗ trợ: Nếu gặp phải các hàm số phức tạp hoặc bài toán khó, bạn có thể sử dụng các phần mềm toán học như WolframAlpha, GeoGebra để hỗ trợ tính toán và kiểm tra lại kết quả của mình.

Việc nắm vững các lưu ý trên sẽ giúp bạn tính toán vận tốc tức thời một cách chính xác và hiệu quả, đồng thời tránh được những lỗi thường gặp trong quá trình làm bài tập.

Vận tốc tức thời là một khái niệm quan trọng trong vật lý, đặc biệt trong các bài toán liên quan đến chuyển động và động lực học. Để tính toán chính xác vận tốc tức thời, bạn cần hiểu rõ các nguyên tắc cơ bản của đạo hàm và ứng dụng của nó trong việc giải quyết các bài toán thực tế.

Một trong những cách tiếp cận phổ biến để xác định vận tốc tức thời là sử dụng đạo hàm của hàm vị trí theo thời gian. Công thức cơ bản là:

\[
v(t) = \lim_{{\Delta t \to 0}} \frac{{\Delta s}}{{\Delta t}} = \frac{{ds}}{{dt}}
\]

Ngoài ra, khi áp dụng trong các bài toán thực tế, hãy chú ý đến đơn vị đo lường, tính chính xác của phép tính, và các điều kiện biên của bài toán. Đặc biệt, đối với các bài toán phức tạp hoặc có tính chất không liên tục, việc tính toán có thể đòi hỏi sự tỉ mỉ và chính xác cao.

Cuối cùng, khi giải quyết các bài toán vận tốc tức thời, hãy lưu ý đến các yếu tố ảnh hưởng đến kết quả như gia tốc, lực tác dụng, và môi trường xung quanh. Việc hiểu rõ các yếu tố này sẽ giúp bạn đạt được kết quả chính xác và có được cái nhìn toàn diện hơn về chuyển động của vật thể.