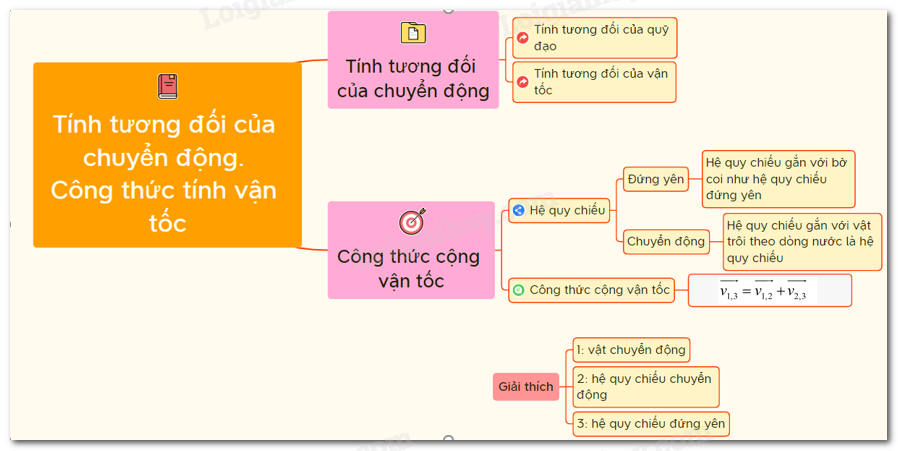
Chủ đề tính vận tốc ngược chiều: Tính vận tốc ngược chiều là kỹ năng quan trọng trong Vật lý, giúp bạn giải quyết các bài toán chuyển động phức tạp. Bài viết này cung cấp hướng dẫn chi tiết từ lý thuyết đến thực hành, cùng với các ví dụ minh họa và bài tập vận dụng để củng cố kiến thức.
Mục lục
- Giới Thiệu Về Tính Vận Tốc Ngược Chiều
- 1. Khái Niệm Cơ Bản Về Vận Tốc Ngược Chiều
- 2. Công Thức Tính Thời Gian Gặp Nhau
- 3. Ví Dụ Minh Họa
- 4. Tình Huống Khởi Hành Không Cùng Lúc
- Kết Luận
- 1. Khái Niệm Cơ Bản Về Vận Tốc Ngược Chiều
- 2. Công Thức Tính Thời Gian Gặp Nhau
- 3. Ví Dụ Minh Họa
- 4. Tình Huống Khởi Hành Không Cùng Lúc
- Kết Luận
- 2. Công Thức Tính Thời Gian Gặp Nhau
- 3. Ví Dụ Minh Họa
- 4. Tình Huống Khởi Hành Không Cùng Lúc
- Kết Luận
- 3. Ví Dụ Minh Họa
- 4. Tình Huống Khởi Hành Không Cùng Lúc
- Kết Luận
- 4. Tình Huống Khởi Hành Không Cùng Lúc
- Kết Luận
- Kết Luận
- 1. Tổng quan về khái niệm vận tốc ngược chiều
- 2. Công thức tính vận tốc ngược chiều
- 3. Các bước giải bài tập vận tốc ngược chiều
- 4. Ví dụ minh họa về bài toán vận tốc ngược chiều
- 5. Bài tập vận dụng và đáp án
- 6. Những lưu ý quan trọng khi học và áp dụng kiến thức vận tốc ngược chiều
Giới Thiệu Về Tính Vận Tốc Ngược Chiều
Trong toán học và vật lý, việc tính vận tốc ngược chiều là một trong những bài toán cơ bản và thường gặp. Đây là một kỹ năng quan trọng giúp học sinh hiểu và giải quyết các bài toán về chuyển động cơ học, đặc biệt là trong các trường hợp hai đối tượng di chuyển theo hướng ngược lại nhau trên cùng một đường thẳng.

.png)
1. Khái Niệm Cơ Bản Về Vận Tốc Ngược Chiều
Khi hai đối tượng di chuyển theo hướng ngược lại nhau, vận tốc tổng hợp của chúng chính là tổng của hai vận tốc cá nhân. Công thức tổng quát để tính vận tốc ngược chiều là:
\[
v = v_1 + v_2
\]
Trong đó:
- \(v_1\): Vận tốc của đối tượng thứ nhất.
- \(v_2\): Vận tốc của đối tượng thứ hai.
2. Công Thức Tính Thời Gian Gặp Nhau
Thời gian để hai đối tượng gặp nhau khi chúng di chuyển ngược chiều có thể được tính bằng công thức:
\[
t = \frac{d}{v_1 + v_2}
\]
Trong đó:
- \(t\): Thời gian gặp nhau.
- \(d\): Khoảng cách ban đầu giữa hai đối tượng.

3. Ví Dụ Minh Họa
Giả sử có hai xe ô tô di chuyển ngược chiều nhau từ hai thành phố cách nhau 120 km. Xe thứ nhất di chuyển với vận tốc \(60 \, \text{km/h}\), và xe thứ hai di chuyển với vận tốc \(40 \, \text{km/h}\). Thời gian để hai xe gặp nhau là:
\[
t = \frac{120 \, \text{km}}{60 \, \text{km/h} + 40 \, \text{km/h}} = \frac{120 \, \text{km}}{100 \, \text{km/h}} = 1.2 \, \text{giờ}
\]
Vậy hai xe sẽ gặp nhau sau 1.2 giờ, tức là sau 1 giờ 12 phút.

4. Tình Huống Khởi Hành Không Cùng Lúc
Nếu hai đối tượng không khởi hành cùng lúc, ta cần điều chỉnh thời gian di chuyển của đối tượng khởi hành trước bằng cách trừ đi khoảng cách mà nó đã đi được trước khi đối tượng kia bắt đầu di chuyển:
\[
t_2 = \frac{d - s_1}{v_1 + v_2}
\]
Trong đó \(s_1 = v_1 \times t_1\) là quãng đường mà đối tượng thứ nhất đã đi trước.

Kết Luận
Việc tính vận tốc ngược chiều là một kỹ năng quan trọng trong học tập và áp dụng thực tế. Hiểu rõ các công thức và cách tính này giúp học sinh giải quyết được nhiều bài toán liên quan đến chuyển động cơ học, từ đó nâng cao khả năng tư duy và áp dụng kiến thức vào cuộc sống.
XEM THÊM:
1. Khái Niệm Cơ Bản Về Vận Tốc Ngược Chiều
Khi hai đối tượng di chuyển theo hướng ngược lại nhau, vận tốc tổng hợp của chúng chính là tổng của hai vận tốc cá nhân. Công thức tổng quát để tính vận tốc ngược chiều là:
\[
v = v_1 + v_2
\]
Trong đó:
- \(v_1\): Vận tốc của đối tượng thứ nhất.
- \(v_2\): Vận tốc của đối tượng thứ hai.

2. Công Thức Tính Thời Gian Gặp Nhau
Thời gian để hai đối tượng gặp nhau khi chúng di chuyển ngược chiều có thể được tính bằng công thức:
\[
t = \frac{d}{v_1 + v_2}
\]
Trong đó:
- \(t\): Thời gian gặp nhau.
- \(d\): Khoảng cách ban đầu giữa hai đối tượng.

3. Ví Dụ Minh Họa
Giả sử có hai xe ô tô di chuyển ngược chiều nhau từ hai thành phố cách nhau 120 km. Xe thứ nhất di chuyển với vận tốc \(60 \, \text{km/h}\), và xe thứ hai di chuyển với vận tốc \(40 \, \text{km/h}\). Thời gian để hai xe gặp nhau là:
\[
t = \frac{120 \, \text{km}}{60 \, \text{km/h} + 40 \, \text{km/h}} = \frac{120 \, \text{km}}{100 \, \text{km/h}} = 1.2 \, \text{giờ}
\]
Vậy hai xe sẽ gặp nhau sau 1.2 giờ, tức là sau 1 giờ 12 phút.
4. Tình Huống Khởi Hành Không Cùng Lúc
Nếu hai đối tượng không khởi hành cùng lúc, ta cần điều chỉnh thời gian di chuyển của đối tượng khởi hành trước bằng cách trừ đi khoảng cách mà nó đã đi được trước khi đối tượng kia bắt đầu di chuyển:
\[
t_2 = \frac{d - s_1}{v_1 + v_2}
\]
Trong đó \(s_1 = v_1 \times t_1\) là quãng đường mà đối tượng thứ nhất đã đi trước.

Kết Luận
Việc tính vận tốc ngược chiều là một kỹ năng quan trọng trong học tập và áp dụng thực tế. Hiểu rõ các công thức và cách tính này giúp học sinh giải quyết được nhiều bài toán liên quan đến chuyển động cơ học, từ đó nâng cao khả năng tư duy và áp dụng kiến thức vào cuộc sống.
2. Công Thức Tính Thời Gian Gặp Nhau
Thời gian để hai đối tượng gặp nhau khi chúng di chuyển ngược chiều có thể được tính bằng công thức:
\[
t = \frac{d}{v_1 + v_2}
\]
Trong đó:
- \(t\): Thời gian gặp nhau.
- \(d\): Khoảng cách ban đầu giữa hai đối tượng.
3. Ví Dụ Minh Họa
Giả sử có hai xe ô tô di chuyển ngược chiều nhau từ hai thành phố cách nhau 120 km. Xe thứ nhất di chuyển với vận tốc \(60 \, \text{km/h}\), và xe thứ hai di chuyển với vận tốc \(40 \, \text{km/h}\). Thời gian để hai xe gặp nhau là:
\[
t = \frac{120 \, \text{km}}{60 \, \text{km/h} + 40 \, \text{km/h}} = \frac{120 \, \text{km}}{100 \, \text{km/h}} = 1.2 \, \text{giờ}
\]
Vậy hai xe sẽ gặp nhau sau 1.2 giờ, tức là sau 1 giờ 12 phút.

4. Tình Huống Khởi Hành Không Cùng Lúc
Nếu hai đối tượng không khởi hành cùng lúc, ta cần điều chỉnh thời gian di chuyển của đối tượng khởi hành trước bằng cách trừ đi khoảng cách mà nó đã đi được trước khi đối tượng kia bắt đầu di chuyển:
\[
t_2 = \frac{d - s_1}{v_1 + v_2}
\]
Trong đó \(s_1 = v_1 \times t_1\) là quãng đường mà đối tượng thứ nhất đã đi trước.
Kết Luận
Việc tính vận tốc ngược chiều là một kỹ năng quan trọng trong học tập và áp dụng thực tế. Hiểu rõ các công thức và cách tính này giúp học sinh giải quyết được nhiều bài toán liên quan đến chuyển động cơ học, từ đó nâng cao khả năng tư duy và áp dụng kiến thức vào cuộc sống.
3. Ví Dụ Minh Họa
Giả sử có hai xe ô tô di chuyển ngược chiều nhau từ hai thành phố cách nhau 120 km. Xe thứ nhất di chuyển với vận tốc \(60 \, \text{km/h}\), và xe thứ hai di chuyển với vận tốc \(40 \, \text{km/h}\). Thời gian để hai xe gặp nhau là:
\[
t = \frac{120 \, \text{km}}{60 \, \text{km/h} + 40 \, \text{km/h}} = \frac{120 \, \text{km}}{100 \, \text{km/h}} = 1.2 \, \text{giờ}
\]
Vậy hai xe sẽ gặp nhau sau 1.2 giờ, tức là sau 1 giờ 12 phút.

4. Tình Huống Khởi Hành Không Cùng Lúc
Nếu hai đối tượng không khởi hành cùng lúc, ta cần điều chỉnh thời gian di chuyển của đối tượng khởi hành trước bằng cách trừ đi khoảng cách mà nó đã đi được trước khi đối tượng kia bắt đầu di chuyển:
\[
t_2 = \frac{d - s_1}{v_1 + v_2}
\]
Trong đó \(s_1 = v_1 \times t_1\) là quãng đường mà đối tượng thứ nhất đã đi trước.
Kết Luận
Việc tính vận tốc ngược chiều là một kỹ năng quan trọng trong học tập và áp dụng thực tế. Hiểu rõ các công thức và cách tính này giúp học sinh giải quyết được nhiều bài toán liên quan đến chuyển động cơ học, từ đó nâng cao khả năng tư duy và áp dụng kiến thức vào cuộc sống.
4. Tình Huống Khởi Hành Không Cùng Lúc
Nếu hai đối tượng không khởi hành cùng lúc, ta cần điều chỉnh thời gian di chuyển của đối tượng khởi hành trước bằng cách trừ đi khoảng cách mà nó đã đi được trước khi đối tượng kia bắt đầu di chuyển:
\[
t_2 = \frac{d - s_1}{v_1 + v_2}
\]
Trong đó \(s_1 = v_1 \times t_1\) là quãng đường mà đối tượng thứ nhất đã đi trước.
Kết Luận
Việc tính vận tốc ngược chiều là một kỹ năng quan trọng trong học tập và áp dụng thực tế. Hiểu rõ các công thức và cách tính này giúp học sinh giải quyết được nhiều bài toán liên quan đến chuyển động cơ học, từ đó nâng cao khả năng tư duy và áp dụng kiến thức vào cuộc sống.
Kết Luận
Việc tính vận tốc ngược chiều là một kỹ năng quan trọng trong học tập và áp dụng thực tế. Hiểu rõ các công thức và cách tính này giúp học sinh giải quyết được nhiều bài toán liên quan đến chuyển động cơ học, từ đó nâng cao khả năng tư duy và áp dụng kiến thức vào cuộc sống.
1. Tổng quan về khái niệm vận tốc ngược chiều
Vận tốc ngược chiều là khái niệm quan trọng trong vật lý học, đặc biệt trong các bài toán về chuyển động. Đây là trường hợp khi hai đối tượng chuyển động về phía nhau, hoặc theo hai hướng ngược nhau trên cùng một trục.
Để hiểu rõ hơn về khái niệm này, chúng ta cần nắm vững các yếu tố cơ bản sau:
- Vận tốc: Đại lượng vật lý đo lường sự thay đổi vị trí của một vật theo thời gian. Được ký hiệu là \(v\), đơn vị đo thường là m/s (mét trên giây).
- Chiều chuyển động: Hướng mà đối tượng đang di chuyển. Chiều chuyển động có thể cùng chiều hoặc ngược chiều nhau.
- Vận tốc ngược chiều: Trường hợp khi hai đối tượng di chuyển với vận tốc khác nhau về phía nhau. Tổng vận tốc trong trường hợp này được tính bằng cách cộng vận tốc của hai đối tượng lại với nhau.
Ví dụ, nếu hai xe đang di chuyển về phía nhau với vận tốc lần lượt là \(v_1 = 60 \, \text{km/h}\) và \(v_2 = 40 \, \text{km/h}\), thì vận tốc ngược chiều giữa chúng sẽ là:
Điều này có nghĩa là khoảng cách giữa hai xe sẽ giảm đi với tốc độ 100 km/h. Khái niệm này thường được áp dụng trong các bài toán về chuyển động trong cùng một trục hoặc trong phân tích các tình huống giao thông thực tế.
2. Công thức tính vận tốc ngược chiều
Vận tốc ngược chiều thường được tính trong các bài toán vật lý liên quan đến chuyển động của hai vật thể di chuyển theo hướng ngược nhau. Công thức tính vận tốc ngược chiều đơn giản dựa trên việc cộng vận tốc của hai vật thể lại với nhau.
Công thức tổng quát để tính vận tốc ngược chiều giữa hai vật thể có vận tốc lần lượt là \(v_1\) và \(v_2\) như sau:
Trong đó:
- \(v_1\): Vận tốc của vật thể thứ nhất (đơn vị: m/s hoặc km/h).
- \(v_2\): Vận tốc của vật thể thứ hai (đơn vị: m/s hoặc km/h).
Ví dụ, nếu một xe hơi đang di chuyển với vận tốc \(v_1 = 60 \, \text{km/h}\) về phía Đông, và một xe khác đang di chuyển với vận tốc \(v_2 = 40 \, \text{km/h}\) về phía Tây, thì vận tốc ngược chiều giữa hai xe sẽ được tính như sau:
Điều này có nghĩa là khoảng cách giữa hai xe giảm đi với tốc độ 100 km/h, hoặc nếu hai xe xuất phát cùng lúc từ hai điểm đối diện nhau, chúng sẽ gặp nhau nhanh hơn với vận tốc tương ứng là 100 km/h.
Trong một số bài toán phức tạp hơn, nếu hai vật thể di chuyển với các góc khác nhau so với trục tọa độ, ta cần sử dụng thêm các công thức liên quan đến vectơ vận tốc và định lý Pythagore để tính toán vận tốc tương đối giữa hai vật thể. Tuy nhiên, trong hầu hết các trường hợp, công thức cộng vận tốc đơn giản ở trên là đủ để giải quyết các bài toán vận tốc ngược chiều.
3. Các bước giải bài tập vận tốc ngược chiều
Để giải bài tập liên quan đến vận tốc ngược chiều, bạn cần tuân theo các bước cụ thể dưới đây nhằm đảm bảo tính chính xác và hiệu quả. Các bước này sẽ giúp bạn tiếp cận bài toán một cách hệ thống và logic.
- Xác định đối tượng và hướng chuyển động:
Đầu tiên, bạn cần xác định rõ đối tượng nào đang chuyển động và hướng di chuyển của chúng. Đối tượng có thể là xe, tàu, người đi bộ, v.v. Hướng chuyển động có thể là về phía nhau (ngược chiều) hoặc ra xa nhau (cùng chiều).
- Thu thập và liệt kê các đại lượng liên quan:
Tiếp theo, bạn cần liệt kê các đại lượng liên quan trong bài toán, chẳng hạn như vận tốc của từng đối tượng \(v_1\), \(v_2\), khoảng cách ban đầu giữa hai đối tượng \(d\), và thời gian \(t\). Đảm bảo rằng các đơn vị đo lường là đồng nhất (ví dụ: tất cả đều là m/s hoặc km/h).
- Áp dụng công thức tính vận tốc ngược chiều:
Sử dụng công thức tổng vận tốc ngược chiều để tính vận tốc chung giữa hai đối tượng:
\[
v_{\text{ngược chiều}} = v_1 + v_2
\]Nếu bài toán yêu cầu tính khoảng cách hoặc thời gian gặp nhau, bạn có thể sử dụng thêm công thức:
\[
d = v_{\text{ngược chiều}} \times t
\]Hoặc:
\[
t = \frac{d}{v_{\text{ngược chiều}}}
\] - Giải và kiểm tra kết quả:
Sau khi áp dụng công thức, hãy tính toán kết quả. Đảm bảo kiểm tra lại các bước và tính toán của bạn để tránh sai sót. Hãy chú ý đến đơn vị của kết quả cuối cùng.
- Viết kết luận và giải thích kết quả:
Cuối cùng, viết kết luận dựa trên kết quả bạn đã tìm được. Nếu cần, hãy giải thích thêm ý nghĩa của kết quả và cách nó phản ánh tình huống thực tế được mô tả trong bài toán.
4. Ví dụ minh họa về bài toán vận tốc ngược chiều
Để hiểu rõ hơn về cách tính vận tốc ngược chiều, chúng ta sẽ xem xét một ví dụ cụ thể dưới đây. Bài toán này sẽ minh họa cách áp dụng các công thức và bước giải đã thảo luận ở trên.
Ví dụ: Hai xe ô tô khởi hành cùng lúc từ hai điểm A và B cách nhau 120 km. Xe thứ nhất khởi hành từ A di chuyển về phía B với vận tốc \(v_1 = 60 \, \text{km/h}\), trong khi xe thứ hai khởi hành từ B di chuyển về phía A với vận tốc \(v_2 = 40 \, \text{km/h}\). Hỏi sau bao lâu thì hai xe gặp nhau?
- Xác định hướng và vận tốc của từng xe:
Xe thứ nhất di chuyển từ A về B với vận tốc \(v_1 = 60 \, \text{km/h}\). Xe thứ hai di chuyển từ B về A với vận tốc \(v_2 = 40 \, \text{km/h}\).
- Tính tổng vận tốc ngược chiều:
Theo công thức đã đề cập, tổng vận tốc ngược chiều của hai xe là:
\[
v_{\text{ngược chiều}} = v_1 + v_2 = 60 \, \text{km/h} + 40 \, \text{km/h} = 100 \, \text{km/h}
\] - Tính thời gian để hai xe gặp nhau:
Sử dụng công thức:
\[
t = \frac{d}{v_{\text{ngược chiều}}}
\]Trong đó \(d = 120 \, \text{km}\) là khoảng cách ban đầu giữa hai xe. Thay các giá trị vào công thức:
\[
t = \frac{120 \, \text{km}}{100 \, \text{km/h}} = 1,2 \, \text{giờ}
\] - Kết luận:
Hai xe sẽ gặp nhau sau 1,2 giờ, hay sau 1 giờ 12 phút kể từ khi bắt đầu di chuyển.
Ví dụ trên minh họa cách giải quyết một bài toán vận tốc ngược chiều, từ việc xác định dữ liệu ban đầu đến tính toán và rút ra kết luận. Điều này giúp củng cố kiến thức và kỹ năng áp dụng công thức một cách hiệu quả.
5. Bài tập vận dụng và đáp án
Để củng cố kiến thức về vận tốc ngược chiều, dưới đây là một số bài tập vận dụng kèm đáp án chi tiết. Các bài tập này sẽ giúp bạn rèn luyện kỹ năng tính toán và áp dụng công thức vào thực tế.
- Bài tập 1:
Hai tàu hỏa bắt đầu di chuyển từ hai điểm A và B cách nhau 300 km, theo hướng ngược chiều nhau. Tàu thứ nhất di chuyển từ A với vận tốc \(v_1 = 80 \, \text{km/h}\), tàu thứ hai di chuyển từ B với vận tốc \(v_2 = 70 \, \text{km/h}\). Hỏi sau bao lâu hai tàu sẽ gặp nhau?
- Giải:
- Bước 1: Xác định tổng vận tốc ngược chiều:
- Bước 2: Tính thời gian gặp nhau:
- Đáp án: Hai tàu sẽ gặp nhau sau 2 giờ.
\[
v_{\text{ngược chiều}} = v_1 + v_2 = 80 \, \text{km/h} + 70 \, \text{km/h} = 150 \, \text{km/h}
\]\[
t = \frac{d}{v_{\text{ngược chiều}}} = \frac{300 \, \text{km}}{150 \, \text{km/h}} = 2 \, \text{giờ}
\] - Bài tập 2:
Hai người đi bộ xuất phát từ hai điểm cách nhau 20 km, di chuyển về phía nhau với vận tốc \(v_1 = 3 \, \text{km/h}\) và \(v_2 = 5 \, \text{km/h}\). Tính thời gian hai người gặp nhau và khoảng cách mỗi người đã đi được khi gặp nhau.
- Giải:
- Bước 1: Tính tổng vận tốc ngược chiều:
- Bước 2: Tính thời gian gặp nhau:
- Bước 3: Tính khoảng cách mỗi người đã đi được:
- Người thứ nhất: \[ d_1 = v_1 \times t = 3 \, \text{km/h} \times 2,5 \, \text{giờ} = 7,5 \, \text{km} \]
- Người thứ hai: \[ d_2 = v_2 \times t = 5 \, \text{km/h} \times 2,5 \, \text{giờ} = 12,5 \, \text{km} \]
- Đáp án: Hai người sẽ gặp nhau sau 2,5 giờ. Người thứ nhất đi được 7,5 km, người thứ hai đi được 12,5 km.
\[
v_{\text{ngược chiều}} = v_1 + v_2 = 3 \, \text{km/h} + 5 \, \text{km/h} = 8 \, \text{km/h}
\]\[
t = \frac{d}{v_{\text{ngược chiều}}} = \frac{20 \, \text{km}}{8 \, \text{km/h}} = 2,5 \, \text{giờ}
\] - Bài tập 3:
Một xe máy khởi hành từ điểm A đi về phía B với vận tốc \(v_1 = 50 \, \text{km/h}\). Một ô tô khởi hành từ B đi về phía A với vận tốc \(v_2 = 80 \, \text{km/h}\). Khoảng cách AB là 260 km. Hỏi sau bao lâu hai xe sẽ gặp nhau? Nếu ô tô xuất phát chậm hơn xe máy 30 phút, thì hai xe gặp nhau ở đâu?
- Giải:
- Bước 1: Tính tổng vận tốc ngược chiều:
- Bước 2: Tính thời gian gặp nhau (nếu khởi hành cùng lúc):
- Bước 3: Tính quãng đường mỗi xe đi được trong 2 giờ:
- Xe máy: \[ d_1 = v_1 \times t = 50 \, \text{km/h} \times 2 \, \text{giờ} = 100 \, \text{km} \]
- Ô tô: \[ d_2 = v_2 \times t = 80 \, \text{km/h} \times 2 \, \text{giờ} = 160 \, \text{km} \]
- Bước 4: Tính vị trí gặp nhau nếu ô tô xuất phát chậm 30 phút:
- Đáp án: Nếu ô tô xuất phát cùng lúc, hai xe sẽ gặp nhau sau 2 giờ. Nếu ô tô xuất phát chậm 30 phút, hai xe gặp nhau cách điểm B khoảng 115,2 km.
\[
v_{\text{ngược chiều}} = v_1 + v_2 = 50 \, \text{km/h} + 80 \, \text{km/h} = 130 \, \text{km/h}
\]\[
t = \frac{d}{v_{\text{ngược chiều}}} = \frac{260 \, \text{km}}{130 \, \text{km/h}} = 2 \, \text{giờ}
\]Trong 30 phút (0,5 giờ), xe máy đi được:
\[
d_1' = v_1 \times 0,5 \, \text{giờ} = 50 \, \text{km/h} \times 0,5 \, \text{giờ} = 25 \, \text{km}
\]Khi ô tô xuất phát, khoảng cách giữa hai xe là \(260 \, \text{km} - 25 \, \text{km} = 235 \, \text{km}\). Thời gian để gặp nhau là:
\[
t' = \frac{235 \, \text{km}}{130 \, \text{km/h}} \approx 1,81 \, \text{giờ}
\]Trong thời gian này, ô tô đi được:
\[
d_2' = v_2 \times t' = 80 \, \text{km/h} \times 1,81 \, \text{giờ} \approx 144,8 \, \text{km}
\]Vị trí gặp nhau cách B khoảng \(260 \, \text{km} - 144,8 \, \text{km} \approx 115,2 \, \text{km}\).
6. Những lưu ý quan trọng khi học và áp dụng kiến thức vận tốc ngược chiều
Việc nắm vững kiến thức về vận tốc ngược chiều là cần thiết để giải quyết các bài toán liên quan một cách hiệu quả. Tuy nhiên, trong quá trình học tập và áp dụng, bạn cần chú ý đến một số điểm quan trọng dưới đây để tránh nhầm lẫn và đạt kết quả chính xác.
- Hiểu rõ bản chất của vận tốc ngược chiều:
Vận tốc ngược chiều là tổng của các vận tốc khi hai vật thể di chuyển về phía nhau. Điều này có nghĩa là khoảng cách giữa chúng sẽ giảm đi nhanh hơn so với khi chúng di chuyển cùng chiều. Hãy đảm bảo bạn luôn phân biệt được vận tốc ngược chiều với các tình huống khác như vận tốc cùng chiều.
- Chú ý đến đơn vị vận tốc và khoảng cách:
Trong quá trình giải bài toán, hãy kiểm tra kỹ đơn vị của vận tốc và khoảng cách. Đảm bảo rằng tất cả các đại lượng đều cùng đơn vị trước khi thực hiện phép tính. Nếu cần, bạn nên đổi đơn vị để tránh sai sót.
- Phân tích kỹ lưỡng đề bài:
Trước khi bắt tay vào giải bài, hãy đọc kỹ đề bài để hiểu rõ các dữ liệu đã cho và yêu cầu của bài toán. Xác định hướng di chuyển, vận tốc của từng đối tượng và khoảng cách ban đầu một cách chính xác.
- Áp dụng đúng công thức:
Vận tốc ngược chiều thường được tính bằng công thức:
\[
v_{\text{ngược chiều}} = v_1 + v_2
\]Và thời gian gặp nhau được tính bằng:
\[
t = \frac{d}{v_{\text{ngược chiều}}}
\]Hãy chắc chắn rằng bạn áp dụng đúng công thức vào từng bước giải bài để tránh sai lầm.
- Kiểm tra lại kết quả:
Sau khi tính toán xong, bạn nên dành thời gian kiểm tra lại các bước và kết quả cuối cùng. Điều này giúp đảm bảo tính chính xác của lời giải và giúp bạn phát hiện sớm các lỗi nếu có.
- Luyện tập thường xuyên:
Cuối cùng, việc luyện tập với nhiều bài toán khác nhau sẽ giúp bạn củng cố kiến thức và nâng cao kỹ năng giải toán. Hãy thực hành đều đặn để trở nên thành thạo hơn.
Những lưu ý trên sẽ giúp bạn học tập và áp dụng kiến thức về vận tốc ngược chiều một cách hiệu quả hơn, tránh được các lỗi phổ biến và đạt được kết quả tốt trong quá trình học tập.