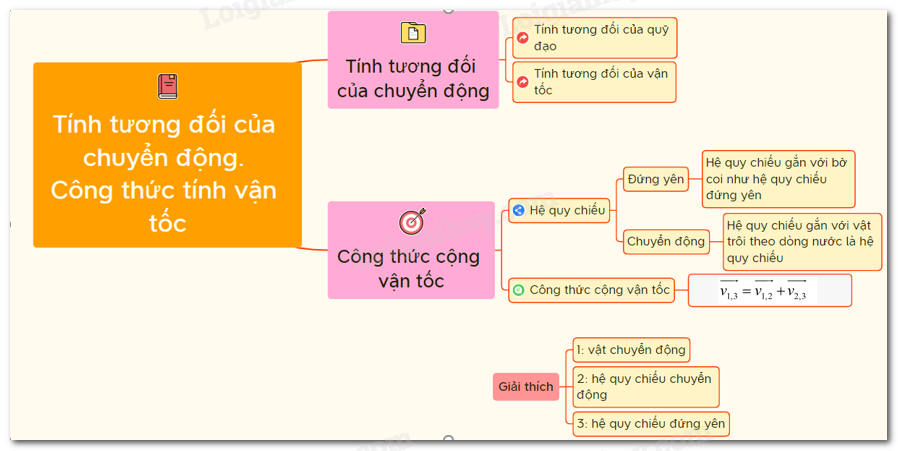
Chủ đề công thức tính vận tốc tổng hợp lớp 10: Máy tính vận tốc là công cụ hữu ích trong việc tính toán tốc độ di chuyển của các vật thể. Bài viết này sẽ cung cấp hướng dẫn chi tiết về cách sử dụng máy tính vận tốc, cùng với các ví dụ minh họa và ứng dụng thực tiễn trong đời sống hàng ngày.
Mục lục
Máy Tính Vận Tốc: Công Thức và Ứng Dụng
Vận tốc là một đại lượng quan trọng trong vật lý và cuộc sống hàng ngày. Nó cho biết tốc độ di chuyển của một đối tượng trong một khoảng thời gian nhất định. Để tính toán vận tốc, ta có thể sử dụng các công thức đơn giản nhưng hiệu quả. Dưới đây là những thông tin chi tiết về cách tính vận tốc và một số ứng dụng thực tiễn của nó.
1. Công Thức Tính Vận Tốc
Công thức cơ bản để tính vận tốc là:
Trong đó:
- \( v \): Vận tốc (m/s hoặc km/h)
- \( s \): Quãng đường di chuyển (m hoặc km)
- \( t \): Thời gian di chuyển (s hoặc h)
2. Ví Dụ Về Tính Vận Tốc
Ví dụ 1: Một xe ô tô đi được quãng đường 150 km trong 3 giờ. Vận tốc của xe là:
Ví dụ 2: Một người chạy 100 m trong 12 giây. Vận tốc của người đó là:
3. Chuyển Đổi Đơn Vị Vận Tốc
Có thể chuyển đổi vận tốc giữa các đơn vị khác nhau. Ví dụ:
- Từ m/s sang km/h: \( v \times 3.6 \)
- Từ km/h sang m/s: \( v \div 3.6 \)
4. Ứng Dụng Của Vận Tốc Trong Đời Sống
Vận tốc được ứng dụng rộng rãi trong nhiều lĩnh vực như giao thông, thể thao, và khoa học. Việc hiểu rõ về vận tốc giúp tối ưu hóa các hoạt động hàng ngày, như lập kế hoạch di chuyển, tập luyện thể dục thể thao, và nghiên cứu khoa học.
Như vậy, việc nắm vững các công thức tính vận tốc và cách chuyển đổi đơn vị không chỉ giúp ích trong học tập mà còn có giá trị thực tiễn lớn trong đời sống.

.png)
I. Giới Thiệu Về Vận Tốc
Vận tốc là một đại lượng vật lý cơ bản, được sử dụng để mô tả tốc độ di chuyển của một vật thể trong một khoảng thời gian cụ thể. Vận tốc không chỉ đo lường tốc độ mà còn cho biết hướng di chuyển của vật thể.
Công thức cơ bản của vận tốc được biểu diễn bằng:
Trong đó:
- \( v \): Vận tốc của vật thể (đơn vị: m/s hoặc km/h)
- \( s \): Quãng đường vật thể di chuyển (đơn vị: mét hoặc kilomet)
- \( t \): Thời gian vật thể di chuyển trên quãng đường đó (đơn vị: giây hoặc giờ)
Vận tốc có thể được phân thành nhiều loại, bao gồm vận tốc trung bình và vận tốc tức thời:
- Vận tốc trung bình: Đây là vận tốc được tính bằng cách chia tổng quãng đường di chuyển cho tổng thời gian di chuyển. Công thức: \[ v_{tb} = \frac{\Delta s}{\Delta t} \]
- Vận tốc tức thời: Đây là vận tốc tại một thời điểm cụ thể, được tính bằng cách lấy giới hạn của vận tốc trung bình khi khoảng thời gian tiến đến giá trị cực nhỏ. Công thức: \[ v = \lim_{\Delta t \to 0} \frac{\Delta s}{\Delta t} = \frac{ds}{dt} \]
Trong thực tế, vận tốc được ứng dụng rộng rãi trong nhiều lĩnh vực như giao thông, thể thao, và công nghệ. Việc hiểu rõ khái niệm và công thức tính toán vận tốc giúp chúng ta tối ưu hóa các hoạt động hàng ngày và đưa ra những quyết định chính xác trong cuộc sống.
II. Công Thức Tính Vận Tốc
Vận tốc là một trong những đại lượng quan trọng trong vật lý, dùng để đo lường mức độ nhanh chậm của một vật thể khi di chuyển. Công thức tính vận tốc khá đơn giản và được ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau.
Công thức cơ bản để tính vận tốc là:
Trong đó:
- \( v \): Vận tốc của vật thể (đơn vị: m/s hoặc km/h)
- \( s \): Quãng đường mà vật thể đã đi được (đơn vị: mét hoặc kilomet)
- \( t \): Thời gian mà vật thể đã di chuyển (đơn vị: giây hoặc giờ)
Có hai loại vận tốc chính cần quan tâm là vận tốc trung bình và vận tốc tức thời:
- Vận tốc trung bình: Đây là vận tốc trung bình của vật thể trong suốt quá trình di chuyển, được tính bằng công thức: \[ v_{tb} = \frac{\Delta s}{\Delta t} \]
- \(\Delta s\): Quãng đường thay đổi
- \(\Delta t\): Thời gian thay đổi
- Vận tốc tức thời: Đây là vận tốc của vật thể tại một thời điểm cụ thể, được tính bằng đạo hàm của quãng đường theo thời gian: \[ v = \frac{ds}{dt} \]
- \(ds\): Một phần rất nhỏ của quãng đường
- \(dt\): Một phần rất nhỏ của thời gian
Trong đó:
Trong đó:
Để tính toán vận tốc, bạn cần xác định rõ các đơn vị đo lường để đảm bảo tính toán chính xác. Khi chuyển đổi giữa các đơn vị, ví dụ từ m/s sang km/h, bạn có thể sử dụng công thức sau:
Vận tốc không chỉ giúp chúng ta hiểu rõ hơn về chuyển động của vật thể mà còn là cơ sở để nghiên cứu các hiện tượng vật lý phức tạp hơn như gia tốc, lực và động năng.

III. Chuyển Đổi Đơn Vị Vận Tốc
Chuyển đổi đơn vị vận tốc là một kỹ năng quan trọng, đặc biệt khi bạn cần so sánh hoặc tính toán các giá trị vận tốc trong các hệ đơn vị khác nhau. Dưới đây là những phương pháp cơ bản để chuyển đổi đơn vị vận tốc giữa các hệ đo lường phổ biến.
1. Chuyển Đổi Từ m/s Sang km/h
Để chuyển đổi vận tốc từ mét trên giây (\(m/s\)) sang kilomet trên giờ (\(km/h\)), bạn sử dụng công thức:
Ví dụ: Một chiếc xe đang di chuyển với vận tốc 10 \(m/s\). Vận tốc này tương đương với:
2. Chuyển Đổi Từ km/h Sang m/s
Ngược lại, để chuyển đổi từ kilomet trên giờ (\(km/h\)) sang mét trên giây (\(m/s\)), bạn dùng công thức:
Ví dụ: Một chiếc xe di chuyển với vận tốc 72 \(km/h\). Vận tốc này tương đương với:
3. Chuyển Đổi Giữa Các Đơn Vị Khác
Ngoài hai đơn vị phổ biến là \(m/s\) và \(km/h\), vận tốc còn có thể được đo bằng nhiều đơn vị khác như dặm trên giờ (mph), hải lý trên giờ (knots). Các công thức chuyển đổi sẽ thay đổi tùy theo đơn vị cụ thể.
- Chuyển từ \(km/h\) sang \(mph\): \[ v_{mph} = v_{km/h} \times 0.621371 \]
- Chuyển từ \(mph\) sang \(km/h\): \[ v_{km/h} = v_{mph} \times 1.60934 \]
- Chuyển từ \(knots\) sang \(km/h\): \[ v_{km/h} = v_{knots} \times 1.852 \]
Việc chuyển đổi đơn vị vận tốc giúp bạn linh hoạt hơn trong các tính toán và ứng dụng thực tiễn, đặc biệt trong các lĩnh vực như giao thông, hàng hải, và hàng không.

IV. Ứng Dụng Thực Tiễn Của Vận Tốc
Vận tốc là một khái niệm quan trọng không chỉ trong vật lý mà còn có rất nhiều ứng dụng thực tiễn trong đời sống hàng ngày. Dưới đây là một số ví dụ điển hình về cách vận tốc được áp dụng trong các lĩnh vực khác nhau:
1. Ứng Dụng Trong Giao Thông
Trong lĩnh vực giao thông, vận tốc là yếu tố cốt lõi để xác định tốc độ của các phương tiện như xe hơi, xe máy, tàu hỏa, và máy bay. Vận tốc giúp thiết kế và điều chỉnh hệ thống đèn giao thông, giới hạn tốc độ trên đường, và tối ưu hóa tuyến đường để giảm thiểu thời gian di chuyển.
- Kiểm soát tốc độ: Các thiết bị như radar và camera được sử dụng để đo vận tốc của các phương tiện, nhằm đảm bảo tuân thủ quy định tốc độ và giảm thiểu tai nạn giao thông.
- Quy hoạch đô thị: Dựa trên vận tốc trung bình của phương tiện, các nhà quy hoạch có thể thiết kế các tuyến đường và hệ thống giao thông hợp lý.
2. Ứng Dụng Trong Thể Thao
Trong thể thao, vận tốc là chỉ số quan trọng để đánh giá hiệu suất của vận động viên. Từ việc đo tốc độ chạy, bơi, đạp xe cho đến các môn thể thao như bóng đá, bóng rổ, vận tốc giúp xác định khả năng và kỹ thuật của các vận động viên.
- Chạy điền kinh: Vận tốc là chỉ số quyết định thành tích của các vận động viên trong các cuộc thi chạy nước rút và marathon.
- Bóng đá: Tốc độ di chuyển của cầu thủ ảnh hưởng trực tiếp đến chiến thuật và khả năng ghi bàn của đội bóng.
3. Ứng Dụng Trong Công Nghệ
Trong công nghệ, vận tốc cũng đóng vai trò quan trọng trong việc tối ưu hóa hiệu suất của các thiết bị và hệ thống.
- Động cơ và máy móc: Vận tốc quay của động cơ ảnh hưởng đến hiệu suất và khả năng làm việc của các loại máy móc.
- Internet và truyền thông: Tốc độ truyền tải dữ liệu (còn được gọi là băng thông) là yếu tố then chốt trong việc đánh giá chất lượng dịch vụ internet và viễn thông.
Nhờ vào những ứng dụng thực tiễn này, vận tốc trở thành một khái niệm không thể thiếu, giúp cải thiện và tối ưu hóa nhiều khía cạnh trong cuộc sống hàng ngày.

V. Các Ví Dụ Minh Họa
Để hiểu rõ hơn về cách tính và áp dụng vận tốc, chúng ta sẽ xem xét một số ví dụ minh họa cụ thể dưới đây:
1. Ví Dụ 1: Tính Vận Tốc Khi Đi Bộ
Giả sử bạn đi bộ từ nhà đến trường, quãng đường dài 2 km, và bạn mất 30 phút để đi hết quãng đường này. Vận tốc trung bình của bạn sẽ được tính như sau:
- Quãng đường \(s = 2 \, km\)
- Thời gian \(t = 30 \, phút = 0.5 \, giờ\)
Vận tốc trung bình:
2. Ví Dụ 2: Tính Vận Tốc Của Xe Hơi
Một chiếc xe hơi di chuyển trên đường cao tốc, đi được quãng đường 120 km trong vòng 1.5 giờ. Vận tốc trung bình của chiếc xe sẽ được tính như sau:
- Quãng đường \(s = 120 \, km\)
- Thời gian \(t = 1.5 \, giờ\)
Vận tốc trung bình:
3. Ví Dụ 3: Tính Vận Tốc Của Máy Bay
Một chiếc máy bay di chuyển từ Hà Nội đến TP. Hồ Chí Minh, quãng đường dài 1,500 km và mất 2 giờ bay. Vận tốc trung bình của máy bay sẽ là:
- Quãng đường \(s = 1500 \, km\)
- Thời gian \(t = 2 \, giờ\)
Vận tốc trung bình:
Những ví dụ trên minh họa cách tính toán và ứng dụng vận tốc trong các tình huống thực tế khác nhau. Việc hiểu rõ và áp dụng chính xác công thức vận tốc giúp chúng ta đưa ra những dự đoán và kế hoạch hợp lý trong cuộc sống hàng ngày.
XEM THÊM:
VI. Kết Luận
Vận tốc là một khái niệm cơ bản nhưng vô cùng quan trọng trong cả lý thuyết và thực tiễn. Từ việc tính toán thời gian di chuyển, thiết kế hệ thống giao thông, đến tối ưu hóa hiệu suất làm việc của máy móc, vận tốc đóng vai trò không thể thiếu. Những kiến thức về cách tính toán và chuyển đổi đơn vị vận tốc không chỉ giúp chúng ta hiểu rõ hơn về thế giới vật lý xung quanh mà còn có thể áp dụng vào nhiều lĩnh vực khác nhau của cuộc sống.
Bằng cách nắm vững các công thức và phương pháp chuyển đổi, chúng ta có thể dễ dàng thực hiện các phép tính liên quan đến vận tốc một cách chính xác. Điều này giúp cải thiện sự hiệu quả trong công việc, tối ưu hóa quá trình học tập và nghiên cứu, đồng thời nâng cao nhận thức về tầm quan trọng của vận tốc trong nhiều khía cạnh khác nhau.
Những ứng dụng thực tiễn của vận tốc, từ giao thông, thể thao, đến công nghệ, đều cho thấy tính hữu ích và rộng rãi của khái niệm này. Vận tốc không chỉ là một đại lượng vật lý, mà còn là công cụ hỗ trợ cho việc giải quyết các vấn đề hàng ngày, giúp chúng ta tiến gần hơn đến các mục tiêu cá nhân và cộng đồng.
Tóm lại, việc hiểu rõ và áp dụng các kiến thức về vận tốc sẽ mở ra nhiều cơ hội và mang lại nhiều lợi ích trong cuộc sống. Dù trong học tập, công việc hay trong các hoạt động hàng ngày, việc nắm bắt tốt khái niệm vận tốc sẽ giúp chúng ta đạt được hiệu suất và kết quả tốt nhất.