Chủ đề cách tính vận tốc tb: Bài viết này sẽ cung cấp cho bạn hướng dẫn chi tiết về cách tính vận tốc trung bình (TB) trong nhiều tình huống khác nhau, từ giao thông đến đời sống hàng ngày. Với những ví dụ minh họa dễ hiểu và công thức cơ bản, bạn sẽ nhanh chóng nắm vững khái niệm vận tốc TB và ứng dụng nó vào thực tế.
Mục lục
Cách Tính Vận Tốc Trung Bình
Vận tốc trung bình là một khái niệm quan trọng trong vật lý và thường được sử dụng trong các bài toán liên quan đến chuyển động. Vận tốc trung bình cho biết tốc độ di chuyển của một vật thể trong một khoảng thời gian xác định.
Công Thức Tính Vận Tốc Trung Bình
Công thức tính vận tốc trung bình được xác định bằng thương số giữa tổng quãng đường vật đi được và tổng thời gian di chuyển:
\[
v_{tb} = \frac{S}{t}
\]
- \(v_{tb}\): Vận tốc trung bình
- \(S\): Quãng đường đi được
- \(t\): Thời gian di chuyển
Ví Dụ Về Cách Tính Vận Tốc Trung Bình
Ví dụ 1: Một xe ô tô đi được quãng đường 180 km trong 3 giờ. Vận tốc trung bình của ô tô là:
\[
v_{tb} = \frac{180 \text{ km}}{3 \text{ giờ}} = 60 \text{ km/giờ}
\]
Ví dụ 2: Một vận động viên chạy được 100 mét trong 10 giây. Vận tốc trung bình của vận động viên là:
\[
v_{tb} = \frac{100 \text{ m}}{10 \text{ s}} = 10 \text{ m/s}
\]
Ứng Dụng Của Vận Tốc Trung Bình Trong Đời Sống
- Giao Thông: Vận tốc trung bình giúp điều chỉnh tốc độ của các phương tiện giao thông để đảm bảo an toàn trên đường.
- Thể Thao: Vận tốc trung bình được sử dụng để đánh giá và nâng cao hiệu suất của các vận động viên trong các môn thể thao như điền kinh, bơi lội.
- Sản Xuất Công Nghiệp: Vận tốc trung bình hỗ trợ kiểm soát tốc độ của các dây chuyền sản xuất, đảm bảo chất lượng sản phẩm.
Các Bài Tập Về Vận Tốc Trung Bình
Câu hỏi: Một xe khách đi từ bến xe đến thành phố. Nửa thời gian đầu vận tốc của xe là 60 km/h, nửa thời gian sau là 40 km/h. Tính vận tốc trung bình của xe trên cả quãng đường.
Lời giải:
Vận tốc trung bình của xe được tính dựa trên tổng quãng đường và tổng thời gian di chuyển, sử dụng công thức:
\[
v_{tb} = \frac{S_1 + S_2}{t_1 + t_2}
\]

.png)
1. Định Nghĩa Vận Tốc Trung Bình
Vận tốc trung bình (TB) là một đại lượng vật lý biểu thị mức độ thay đổi vị trí của một vật thể trong một khoảng thời gian nhất định. Vận tốc TB được tính bằng tỉ số giữa quãng đường di chuyển và khoảng thời gian thực hiện chuyển động.
Công thức tính vận tốc trung bình:
\[
v_{tb} = \frac{s}{t}
\]
Trong đó:
- \(v_{tb}\) là vận tốc trung bình
- \(s\) là quãng đường di chuyển (đơn vị: mét)
- \(t\) là thời gian di chuyển (đơn vị: giây)
Vận tốc trung bình có thể được sử dụng để đo lường hiệu suất di chuyển của một vật thể, cho phép phân tích và so sánh tốc độ của nhiều loại chuyển động khác nhau, từ phương tiện giao thông đến các vật thể trong tự nhiên. Đối với các bài toán thực tế, việc tính toán vận tốc TB giúp dự đoán thời gian và quãng đường, tạo điều kiện cho việc quản lý thời gian và tối ưu hóa lộ trình.
2. Công Thức Tính Vận Tốc Trung Bình
Công thức tính vận tốc trung bình được xác định như sau:
- Quãng đường di chuyển: Ký hiệu là \(S\), là tổng độ dài quãng đường mà vật đã di chuyển từ điểm bắt đầu đến điểm kết thúc.
- Thời gian di chuyển: Ký hiệu là \(t\), là tổng thời gian vật đã di chuyển trên quãng đường \(S\).
- Công thức tính vận tốc trung bình:
Vận tốc trung bình \(v_{\text{tb}}\) được tính bằng công thức:
\[
v_{\text{tb}} = \frac{S}{t}
\]
Trong đó:
- \(v_{\text{tb}}\) là vận tốc trung bình.
- \(S\) là quãng đường đã di chuyển.
- \(t\) là thời gian di chuyển.
Ví dụ, nếu một xe di chuyển 100 km trong 2 giờ, thì vận tốc trung bình của xe là:
\[
v_{\text{tb}} = \frac{100 \text{ km}}{2 \text{ giờ}} = 50 \text{ km/h}
\]

3. Ứng Dụng Của Vận Tốc Trung Bình
Vận tốc trung bình không chỉ là một khái niệm trong vật lý mà còn có nhiều ứng dụng thực tế trong đời sống hàng ngày và công nghiệp. Dưới đây là một số ứng dụng nổi bật của vận tốc trung bình:
- Ứng dụng trong giao thông: Vận tốc trung bình được sử dụng để tính toán và kiểm soát tốc độ di chuyển của các phương tiện giao thông như ô tô, xe máy, tàu hỏa. Điều này giúp điều chỉnh tốc độ để đảm bảo an toàn giao thông. Ví dụ, nếu một chiếc xe di chuyển 120 km trong 2 giờ, vận tốc trung bình của nó là \( v = \frac{120 \, \text{km}}{2 \, \text{giờ}} = 60 \, \text{km/giờ} \).
- Ứng dụng trong thể thao: Trong các môn thể thao như điền kinh hay bơi lội, vận tốc trung bình được dùng để đánh giá hiệu suất của vận động viên. Ví dụ, nếu một vận động viên chạy 100 mét trong 10 giây, vận tốc trung bình của anh ta là \( v = \frac{100 \, \text{m}}{10 \, \text{s}} = 10 \, \text{m/s} \).
- Ứng dụng trong sản xuất công nghiệp: Vận tốc trung bình được sử dụng để tối ưu hóa tốc độ của các dây chuyền sản xuất, đảm bảo hiệu suất và chất lượng sản phẩm. Ví dụ, một dây chuyền sản xuất có thể vận chuyển 1000 sản phẩm mỗi giờ, với vận tốc trung bình là \( v = \frac{1000 \, \text{sản phẩm}}{1 \, \text{giờ}} = 1000 \, \text{sản phẩm/giờ} \).
- Ứng dụng trong công nghệ hàng không: Trong lĩnh vực hàng không, vận tốc trung bình được dùng để tính toán tốc độ bay của máy bay, giúp đảm bảo an toàn và hiệu quả trong quá trình bay.
Với những ứng dụng đa dạng này, vận tốc trung bình đã trở thành một yếu tố không thể thiếu trong nhiều lĩnh vực của cuộc sống và sản xuất hiện đại.
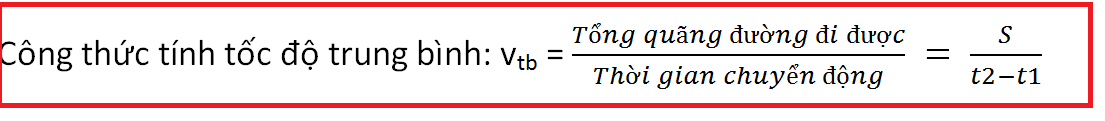
4. Ví Dụ Minh Họa Tính Vận Tốc Trung Bình
Dưới đây là một số ví dụ minh họa cụ thể về cách tính vận tốc trung bình trong các tình huống thực tế:
- Ví dụ 1: Một xe ô tô di chuyển từ Hà Nội đến Hải Phòng, quãng đường là 120 km. Nếu thời gian di chuyển hết 2 giờ, vận tốc trung bình của xe là: \[ v_{\text{tb}} = \frac{S}{t} = \frac{120 \, \text{km}}{2 \, \text{giờ}} = 60 \, \text{km/giờ} \]
- Ví dụ 2: Một vận động viên chạy 400 mét trong 50 giây. Vận tốc trung bình của vận động viên đó là: \[ v_{\text{tb}} = \frac{S}{t} = \frac{400 \, \text{m}}{50 \, \text{s}} = 8 \, \text{m/s} \]
- Ví dụ 3: Một tàu hỏa đi từ thành phố A đến thành phố B với quãng đường 300 km trong 5 giờ. Vận tốc trung bình của tàu hỏa là: \[ v_{\text{tb}} = \frac{S}{t} = \frac{300 \, \text{km}}{5 \, \text{giờ}} = 60 \, \text{km/giờ} \]
- Ví dụ 4: Một người đi bộ từ nhà đến công viên, quãng đường là 2 km và mất 30 phút. Vận tốc trung bình của người đó là: \[ v_{\text{tb}} = \frac{S}{t} = \frac{2 \, \text{km}}{0.5 \, \text{giờ}} = 4 \, \text{km/giờ} \]
Những ví dụ trên giúp bạn hiểu rõ hơn về cách tính vận tốc trung bình trong nhiều tình huống khác nhau, từ giao thông, thể thao đến các hoạt động hàng ngày.

5. Các Bài Tập Tính Vận Tốc Trung Bình
Dưới đây là một số bài tập tính vận tốc trung bình, giúp bạn rèn luyện và áp dụng các công thức đã học vào thực tế:
- Bài tập 1: Một xe máy đi quãng đường 150 km trong 3 giờ đầu, sau đó tiếp tục đi thêm 50 km trong 1 giờ nữa. Tính vận tốc trung bình của xe máy trong toàn bộ hành trình. \[ v_{\text{tb}} = \frac{S_{\text{tổng}}}{t_{\text{tổng}}} = \frac{150 \, \text{km} + 50 \, \text{km}}{3 \, \text{giờ} + 1 \, \text{giờ}} = \frac{200 \, \text{km}}{4 \, \text{giờ}} = 50 \, \text{km/giờ} \]
- Bài tập 2: Một người đi bộ với vận tốc trung bình 5 km/h trong 2 giờ đầu và 4 km/h trong 3 giờ tiếp theo. Tính vận tốc trung bình của người đó trong cả quãng đường. \[ v_{\text{tb}} = \frac{S_1 + S_2}{t_1 + t_2} = \frac{(5 \, \text{km/h} \times 2 \, \text{giờ}) + (4 \, \text{km/h} \times 3 \, \text{giờ})}{2 \, \text{giờ} + 3 \, \text{giờ}} = \frac{10 \, \text{km} + 12 \, \text{km}}{5 \, \text{giờ}} = 4.4 \, \text{km/giờ} \]
- Bài tập 3: Một tàu chạy được 100 km với vận tốc 80 km/h, sau đó giảm vận tốc còn 60 km/h trong 2 giờ tiếp theo. Tính vận tốc trung bình của tàu trên cả hành trình.
- Bài tập 4: Một vận động viên bơi 200 mét trong 50 giây và sau đó bơi thêm 300 mét trong 75 giây. Hãy tính vận tốc trung bình của vận động viên đó. \[ v_{\text{tb}} = \frac{S_1 + S_2}{t_1 + t_2} = \frac{200 \, \text{m} + 300 \, \text{m}}{50 \, \text{giây} + 75 \, \text{giây}} = \frac{500 \, \text{m}}{125 \, \text{giây}} = 4 \, \text{m/s} \]
Những bài tập này giúp bạn củng cố kiến thức về vận tốc trung bình, đồng thời phát triển kỹ năng giải quyết bài toán liên quan đến chuyển động.












