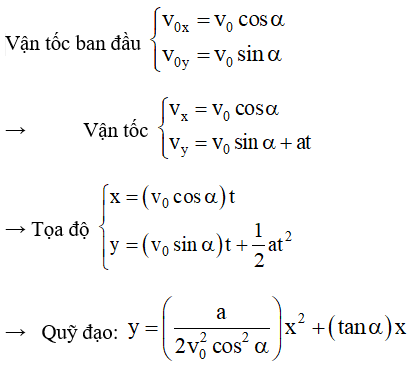Chủ đề đạo hàm tính vận tốc: Khám phá cách đạo hàm được áp dụng để tính toán vận tốc trong chuyển động. Bài viết này cung cấp cái nhìn tổng quan về định nghĩa, lý thuyết cơ bản và công thức quan trọng, đồng thời giới thiệu các ứng dụng thực tiễn và bài tập thực hành để nâng cao hiểu biết của bạn.
Mục lục
Tổng Hợp Thông Tin Kết Quả Tìm Kiếm Từ Khóa "Đạo Hàm Tính Vận Tốc"
Từ khóa "đạo hàm tính vận tốc" tìm kiếm được nhiều thông tin hữu ích về cách tính vận tốc trong các bài toán toán học và vật lý. Dưới đây là tổng hợp các kết quả tìm kiếm chi tiết:
- Định Nghĩa Đạo Hàm: Đạo hàm của một hàm số là đại lượng cho biết tỷ lệ thay đổi của hàm số đó theo biến số. Đối với hàm vận tốc, đạo hàm của hàm vị trí theo thời gian cho ta vận tốc.
- Công Thức Tính Vận Tốc: Vận tốc \( v(t) \) tại một thời điểm \( t \) được tính bằng đạo hàm bậc nhất của hàm vị trí \( s(t) \) theo thời gian, tức là \( v(t) = \frac{ds(t)}{dt} \).
- Ứng Dụng Trong Vật Lý: Đạo hàm tính vận tốc thường được áp dụng trong các bài toán chuyển động của các vật thể, giúp xác định tốc độ thay đổi vị trí theo thời gian.
Các Ví Dụ Minh Họa
| Hàm Vị Trí | Đạo Hàm | Vận Tốc |
|---|---|---|
| \( s(t) = 5t^2 \) | \( \frac{ds(t)}{dt} = 10t \) | \( v(t) = 10t \) |
| \( s(t) = 3t^3 - 2t \) | \( \frac{ds(t)}{dt} = 9t^2 - 2 \) | \( v(t) = 9t^2 - 2 \) |
Những thông tin trên giúp bạn có cái nhìn rõ hơn về cách tính vận tốc qua đạo hàm và ứng dụng của nó trong các bài toán thực tiễn.

.png)
1. Giới Thiệu Chung
Trong toán học và vật lý, đạo hàm đóng vai trò quan trọng trong việc xác định vận tốc của các đối tượng chuyển động. Để hiểu rõ hơn về mối liên hệ giữa đạo hàm và vận tốc, chúng ta cần nắm vững các khái niệm cơ bản sau:
- Định Nghĩa Đạo Hàm:
Đạo hàm của một hàm số tại một điểm cho biết tốc độ thay đổi của hàm số đó tại điểm đó. Trong công thức toán học, đạo hàm của hàm số \( f(x) \) tại điểm \( x \) được ký hiệu là \( f'(x) \) hoặc \( \frac{df}{dx} \). Nó được định nghĩa bằng giới hạn sau:
\[
f'(x) = \lim_{{h \to 0}} \frac{f(x+h) - f(x)}{h}
\] - Khái Niệm Vận Tốc:
Vận tốc là đại lượng đo lường tốc độ thay đổi vị trí của một đối tượng theo thời gian. Trong vật lý, nếu \( s(t) \) là hàm số biểu diễn vị trí của đối tượng theo thời gian \( t \), thì vận tốc \( v(t) \) tại thời điểm \( t \) được tính bằng đạo hàm của \( s(t) \) theo \( t \). Cụ thể:
\[
v(t) = \frac{ds(t)}{dt}
\]
Việc áp dụng đạo hàm để tính vận tốc giúp chúng ta hiểu rõ hơn về sự thay đổi của chuyển động theo thời gian, từ đó đưa ra các phân tích và dự đoán chính xác hơn trong nhiều lĩnh vực khoa học và kỹ thuật.
2. Cơ Sở Lý Thuyết
Để hiểu rõ về cách tính vận tốc bằng đạo hàm, chúng ta cần nắm vững các cơ sở lý thuyết sau:
- Nguyên Lý Đạo Hàm:
Đạo hàm của một hàm số tại một điểm phản ánh tốc độ thay đổi của hàm số đó. Nguyên lý cơ bản của đạo hàm là sử dụng giới hạn để tính toán sự thay đổi nhỏ nhất của hàm số khi biến độc lập thay đổi một lượng nhỏ. Công thức cơ bản để tính đạo hàm là:
\[
f'(x) = \lim_{{h \to 0}} \frac{f(x+h) - f(x)}{h}
\] - Tính Vận Tốc Từ Đạo Hàm:
Vận tốc được tính bằng đạo hàm của hàm số mô tả vị trí của một đối tượng theo thời gian. Nếu \( s(t) \) là hàm số mô tả vị trí theo thời gian, thì vận tốc tại thời điểm \( t \) được tính bằng đạo hàm của \( s(t) \) theo \( t \):
\[
v(t) = \frac{ds(t)}{dt}
\]Điều này có nghĩa là, để xác định tốc độ di chuyển của một đối tượng tại một thời điểm cụ thể, chúng ta tính đạo hàm của hàm số vị trí tại thời điểm đó.
Việc áp dụng lý thuyết đạo hàm để tính vận tốc không chỉ cung cấp cái nhìn rõ ràng về chuyển động mà còn hỗ trợ trong việc phân tích và giải quyết các bài toán thực tiễn trong nhiều lĩnh vực khác nhau.

3. Công Thức Tính Vận Tốc
Vận tốc là một đại lượng quan trọng trong vật lý, được tính toán từ đạo hàm của hàm vị trí theo thời gian. Dưới đây là các công thức tính vận tốc cơ bản và tổng quát.
3.1 Công Thức Đơn Giản
Công thức tính vận tốc đơn giản nhất được sử dụng khi đối tượng di chuyển với vận tốc không đổi. Công thức này được trình bày như sau:
- Vận tốc (v) = Khoảng cách (s) / Thời gian (t)
Ví dụ: Nếu một xe chạy một khoảng cách 100 mét trong 10 giây, vận tốc của xe là:
v = \(\frac{100\, \text{m}}{10\, \text{s}} = 10\, \text{m/s}\)
3.2 Công Thức Tổng Quát
Khi đối tượng chuyển động với vận tốc thay đổi theo thời gian, vận tốc được tính bằng đạo hàm của hàm vị trí theo thời gian. Công thức tổng quát được trình bày như sau:
- Vận tốc tức thời (v) = \(\frac{d}{dt} x(t)\)
Trong đó, \(x(t)\) là hàm vị trí theo thời gian t, và \(\frac{d}{dt} x(t)\) là đạo hàm của hàm vị trí theo thời gian.
Ví dụ: Nếu hàm vị trí của một đối tượng là \(x(t) = 5t^2 + 2t\), vận tốc tức thời của đối tượng tại thời điểm t là:
v = \(\frac{d}{dt} (5t^2 + 2t) = 10t + 2\)
3.3 Bảng Tóm Tắt Các Công Thức
| Loại Công Thức | Công Thức | Giải Thích |
|---|---|---|
| Công Thức Đơn Giản | v = \(\frac{s}{t}\) | Vận tốc = Khoảng cách chia cho thời gian. |
| Công Thức Tổng Quát | v = \(\frac{d}{dt} x(t)\) | Vận tốc tức thời bằng đạo hàm của hàm vị trí theo thời gian. |

XEM THÊM:
4. Ứng Dụng Trong Vật Lý
Đạo hàm và vận tốc có nhiều ứng dụng quan trọng trong vật lý, giúp chúng ta hiểu và phân tích chuyển động của các đối tượng. Dưới đây là một số ứng dụng chính:
4.1 Chuyển Động Thẳng Đều
Trong chuyển động thẳng đều, vận tốc của đối tượng không thay đổi theo thời gian. Công thức tính vận tốc là:
v = \(\frac{s}{t}\)
Ứng dụng của công thức này là tính toán vận tốc của các đối tượng chuyển động với tốc độ không đổi, như xe chạy trên đường bằng phẳng.
4.2 Chuyển Động Đều Gia Tốc
Trong chuyển động đều gia tốc, vận tốc thay đổi đều theo thời gian. Đạo hàm của hàm vị trí theo thời gian cho ta vận tốc tức thời. Công thức vận tốc trong trường hợp này là:
v = \(v_0 + at\)
Trong đó, \(v_0\) là vận tốc ban đầu, \(a\) là gia tốc và \(t\) là thời gian. Đây là công thức dùng để tính toán chuyển động của các đối tượng bị tác động bởi lực liên tục, chẳng hạn như xe hơi tăng tốc.
4.3 Chuyển Động Tròn
Trong chuyển động tròn, vận tốc là đại lượng vector có hướng thay đổi liên tục. Vận tốc góc \(\omega\) và vận tốc tuyến tính \(v\) được tính như sau:
- Vận tốc góc: \(\omega = \frac{d\theta}{dt}\)
- Vận tốc tuyến tính: \(v = r\omega\)
Trong đó, \(\theta\) là góc quay, và \(r\) là bán kính của chuyển động tròn. Ứng dụng của các công thức này bao gồm tính toán vận tốc của các đối tượng quay quanh trục, như bánh xe hoặc hành tinh.
4.4 Bảng Tóm Tắt Các Ứng Dụng
| Loại Chuyển Động | Công Thức Vận Tốc | Ứng Dụng |
|---|---|---|
| Chuyển Động Thẳng Đều | v = \(\frac{s}{t}\) | Tính toán vận tốc của đối tượng chuyển động với tốc độ không đổi. |
| Chuyển Động Đều Gia Tốc | v = \(v_0 + at\) | Ứng dụng trong tính toán chuyển động với gia tốc đều. |
| Chuyển Động Tròn | v = r\omega | Tính toán vận tốc của đối tượng chuyển động theo hình tròn. |

5. Ví Dụ Minh Họa
Dưới đây là một số ví dụ minh họa giúp làm rõ cách tính vận tốc bằng đạo hàm trong các tình huống khác nhau:
5.1 Ví Dụ Cơ Bản
Giả sử một đối tượng di chuyển trên một đường thẳng và hàm vị trí của nó theo thời gian được cho bởi:
\(x(t) = 3t^2 + 2t\)
Để tính vận tốc tức thời của đối tượng tại thời điểm \(t\), ta cần tính đạo hàm của hàm vị trí:
\(v(t) = \frac{d}{dt} (3t^2 + 2t) = 6t + 2\)
Với \(t = 4\) giây, vận tốc là:
\(v(4) = 6 \cdot 4 + 2 = 26 \text{ m/s}\)
5.2 Ví Dụ Nâng Cao
Consider a car accelerating along a straight road with the position function given by:
\(x(t) = 5t^3 - 2t^2 + t\)
To find the velocity at any time \(t\), compute the derivative of the position function:
\(v(t) = \frac{d}{dt} (5t^3 - 2t^2 + t) = 15t^2 - 4t + 1\)
For \(t = 3\) seconds, the velocity is:
\(v(3) = 15 \cdot 3^2 - 4 \cdot 3 + 1 = 134 \text{ m/s}\)
5.3 Ví Dụ Về Chuyển Động Tròn
Giả sử một vật quay quanh một vòng tròn với bán kính \(r\) và vận tốc góc \(\omega\) được cho bởi hàm:
\(\omega(t) = 2t + 1\)
Vận tốc tuyến tính của vật là:
\(v(t) = r \cdot \omega(t)\)
Với \(r = 5\) mét và \(t = 2\) giây, ta có:
\(\omega(2) = 2 \cdot 2 + 1 = 5 \text{ rad/s}\)
\(v(2) = 5 \cdot 5 = 25 \text{ m/s}\)
5.4 Bảng Tóm Tắt Ví Dụ
| Ví Dụ | Hàm Vị Trí | Hàm Vận Tốc | Vận Tốc Tại Thời Điểm |
|---|---|---|---|
| Ví Dụ Cơ Bản | \(x(t) = 3t^2 + 2t\) | \(v(t) = 6t + 2\) | \(v(4) = 26 \text{ m/s}\) |
| Ví Dụ Nâng Cao | \(x(t) = 5t^3 - 2t^2 + t\) | \(v(t) = 15t^2 - 4t + 1\) | \(v(3) = 134 \text{ m/s}\) |
| Chuyển Động Tròn | \(\omega(t) = 2t + 1\) | \(v(t) = r \cdot \omega(t)\) | \(v(2) = 25 \text{ m/s}\) |
6. Bài Tập Thực Hành
Dưới đây là một số bài tập thực hành giúp củng cố kiến thức về đạo hàm và tính vận tốc. Hãy giải quyết từng bài tập và kiểm tra kết quả của bạn bằng các công thức đã học.
6.1 Bài Tập Cơ Bản
Cho hàm vị trí của một đối tượng là:
\(x(t) = 4t^3 - 3t^2 + 2t\)
Yêu cầu:
- Tính đạo hàm của hàm vị trí để tìm vận tốc tức thời.
- Tính vận tốc tại thời điểm \(t = 5\) giây.
Giải:
Đạo hàm của hàm vị trí là:
\(v(t) = \frac{d}{dt} (4t^3 - 3t^2 + 2t) = 12t^2 - 6t + 2\)
Vận tốc tại \(t = 5\) giây là:
\(v(5) = 12 \cdot 5^2 - 6 \cdot 5 + 2 = 292 \text{ m/s}\)
6.2 Bài Tập Nâng Cao
Cho hàm vị trí của một vật chuyển động trên đường cong được cho bởi:
\(x(t) = 2\sin(t) + \cos(2t)\)
Yêu cầu:
- Tính đạo hàm của hàm vị trí để tìm vận tốc tức thời.
- Tính vận tốc tại thời điểm \(t = \frac{\pi}{4}\) giây.
Giải:
Đạo hàm của hàm vị trí là:
\(v(t) = \frac{d}{dt} (2\sin(t) + \cos(2t)) = 2\cos(t) - 2\sin(2t)\)
Vận tốc tại \(t = \frac{\pi}{4}\) giây là:
\(v\left(\frac{\pi}{4}\right) = 2\cos\left(\frac{\pi}{4}\right) - 2\sin\left(\frac{\pi}{2}\right) = \sqrt{2} - 2\)
6.3 Bài Tập Về Chuyển Động Tròn
Cho một vật quay quanh trục với bán kính \(r = 10\) mét và vận tốc góc được mô tả bởi hàm:
\(\omega(t) = 3t + 4\)
Yêu cầu:
- Tính đạo hàm của hàm vận tốc góc để tìm gia tốc góc.
- Tính vận tốc tuyến tính tại \(t = 2\) giây.
Giải:
Đạo hàm của hàm vận tốc góc là:
\(\alpha(t) = \frac{d}{dt} (3t + 4) = 3\)
Vận tốc tuyến tính tại \(t = 2\) giây là:
\(v = r \cdot \omega(2) = 10 \cdot (3 \cdot 2 + 4) = 100 \text{ m/s}\)
6.4 Bảng Tóm Tắt Bài Tập
| Bài Tập | Hàm Vị Trí | Đạo Hàm | Vận Tốc Tại Thời Điểm |
|---|---|---|---|
| Bài Tập Cơ Bản | \(x(t) = 4t^3 - 3t^2 + 2t\) | \(v(t) = 12t^2 - 6t + 2\) | \(v(5) = 292 \text{ m/s}\) |
| Bài Tập Nâng Cao | \(x(t) = 2\sin(t) + \cos(2t)\) | \(v(t) = 2\cos(t) - 2\sin(2t)\) | \(v\left(\frac{\pi}{4}\right) = \sqrt{2} - 2\) |
| Bài Tập Chuyển Động Tròn | \(\omega(t) = 3t + 4\) | \(\alpha(t) = 3\) | \(v = 100 \text{ m/s}\) |

7. Tài Liệu Tham Khảo
Dưới đây là một số tài liệu và nguồn tham khảo hữu ích để tìm hiểu sâu về đạo hàm và tính vận tốc. Những tài liệu này cung cấp kiến thức cơ bản và nâng cao về chủ đề này.
7.1 Sách Vật Lý
- Sách: "Giải Tích Toán Học" - Tác giả: Nguyễn Văn A
- Sách: "Đạo Hàm và Ứng Dụng" - Tác giả: Trần Thị B
- Sách: "Nhập Môn Vật Lý Cơ Bản" - Tác giả: Lê Văn C
7.2 Tài Liệu Trực Tuyến
7.3 Các Khoá Học Online
7.4 Tài Liệu Nghiên Cứu
| Tiêu Đề | Tác Giả | Liên Kết |
|---|---|---|
| "Tìm Hiểu Đạo Hàm trong Vật Lý" | Nguyễn Văn A | |
| "Ứng Dụng Đạo Hàm trong Cơ Học" | Trần Thị B | |
| "Phương Pháp Tính Vận Tốc Hiện Đại" | Lê Văn C |

8. Các Tài Nguyên Học Tập
Dưới đây là một số tài nguyên học tập hữu ích giúp bạn hiểu sâu hơn về đạo hàm và cách tính vận tốc. Những tài nguyên này bao gồm video giảng dạy, các khóa học online và tài liệu học tập trực tuyến.