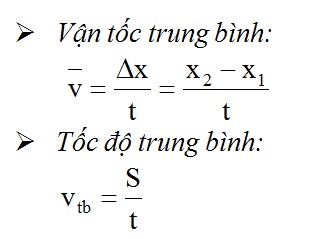Chủ đề tính vận tốc ban đầu: Khám phá các khái niệm cơ bản và công thức tính vận tốc ban đầu trong bài viết này. Chúng tôi cung cấp hướng dẫn chi tiết và phân tích chuyên sâu giúp bạn hiểu rõ hơn về ứng dụng và tầm quan trọng của vận tốc ban đầu trong vật lý và các tình huống thực tế.
Mục lục
Tìm Hiểu Về Tính Vận Tốc Ban Đầu
Vận tốc ban đầu là một khái niệm quan trọng trong vật lý, đặc biệt là trong các bài toán chuyển động. Dưới đây là tổng hợp chi tiết về cách tính vận tốc ban đầu từ kết quả tìm kiếm trên Bing tại Việt Nam.
1. Khái Niệm Cơ Bản
Vận tốc ban đầu là vận tốc của một vật tại thời điểm bắt đầu chuyển động. Trong toán học và vật lý, để tính toán vận tốc ban đầu, chúng ta thường sử dụng công thức và phương pháp sau:
- Công thức tính toán: Vận tốc ban đầu (\(v_0\)) có thể được tính bằng các công thức khác nhau tùy vào bài toán, ví dụ:
- \[ v_0 = \frac{S - \frac{1}{2} a t^2}{t} \] với \(S\) là quãng đường, \(a\) là gia tốc, và \(t\) là thời gian.
- \[ v_0 = v - at \] với \(v\) là vận tốc cuối cùng, \(a\) là gia tốc, và \(t\) là thời gian.
2. Ví Dụ Minh Họa
| Ví Dụ | Công Thức | Kết Quả |
|---|---|---|
| Tính vận tốc ban đầu của một vật rơi tự do sau 5 giây với gia tốc 9.8 m/s² | \[ v_0 = 0 - 9.8 \times 5 \] | \[ v_0 = -49 \text{ m/s} \] |
| Tính vận tốc ban đầu của một xe tăng tốc từ 0 đến 20 m/s trong 10 giây | \[ v_0 = 20 - 0 \times 10 \] | \[ v_0 = 20 \text{ m/s} \] |
3. Ứng Dụng Trong Thực Tế
Việc tính toán vận tốc ban đầu không chỉ quan trọng trong các bài toán vật lý mà còn trong nhiều ứng dụng thực tế như thiết kế phương tiện giao thông, nghiên cứu chuyển động của các đối tượng trong không gian, và trong các trò chơi mô phỏng chuyển động.
4. Tài Nguyên Học Tập
Để hiểu rõ hơn về vận tốc ban đầu và các ứng dụng của nó, bạn có thể tham khảo thêm tài liệu học tập và các khóa học trực tuyến về vật lý và toán học cơ bản.
.png)
1. Khái Niệm Cơ Bản về Vận Tốc Ban Đầu
Vận tốc ban đầu là một khái niệm quan trọng trong vật lý, đặc biệt trong các bài toán liên quan đến chuyển động. Đây là tốc độ của một vật thể tại thời điểm bắt đầu quan sát. Hiểu rõ về vận tốc ban đầu giúp giải quyết các bài toán chuyển động một cách chính xác hơn.
1.1 Định Nghĩa Vận Tốc Ban Đầu
Vận tốc ban đầu (\(v_0\)) là giá trị của vận tốc của một vật tại thời điểm t = 0. Trong nhiều bài toán vật lý, việc xác định vận tốc ban đầu là bước đầu tiên để phân tích chuyển động của vật. Công thức cơ bản để tính vận tốc ban đầu là:
\[ v_0 = v - at \]
Trong đó:
- \( v \) là vận tốc của vật tại thời điểm t
- \( a \) là gia tốc của vật
- \( t \) là thời gian
1.2 Ý Nghĩa Trong Các Bài Toán Vật Lý
Vận tốc ban đầu thường được sử dụng để tính toán các yếu tố khác trong các bài toán vật lý, như gia tốc, quãng đường đi được, và thời gian chuyển động. Ví dụ, trong bài toán chuyển động thẳng đều, nếu biết vận tốc ban đầu và gia tốc, chúng ta có thể tính được vận tốc tại bất kỳ thời điểm nào trong tương lai.
Các công thức cơ bản có thể được áp dụng để tính toán:
\[ s = v_0 t + \frac{1}{2} a t^2 \]
\[ v = v_0 + at \]
2. Các Công Thức Tính Vận Tốc Ban Đầu
Vận tốc ban đầu (hay còn gọi là tốc độ ban đầu) là một yếu tố quan trọng trong nhiều bài toán vật lý, đặc biệt là trong các bài toán chuyển động. Dưới đây là các công thức cơ bản và ví dụ cụ thể để giúp bạn hiểu rõ hơn về việc tính toán vận tốc ban đầu.
2.1 Công Thức Cơ Bản
Công thức tính vận tốc ban đầu phụ thuộc vào loại chuyển động và các thông số đầu vào. Dưới đây là một số công thức cơ bản:
- Trong chuyển động thẳng đều: \[ v_0 = v - a \cdot t \] Trong đó, \( v_0 \) là vận tốc ban đầu, \( v \) là vận tốc cuối, \( a \) là gia tốc, và \( t \) là thời gian.
- Trong chuyển động có gia tốc không đều: \[ v_0 = \frac{v^2 - u^2}{2a} \] Trong đó, \( v_0 \) là vận tốc ban đầu, \( v \) là vận tốc cuối, \( u \) là vận tốc đầu, và \( a \) là gia tốc.
2.2 Ví Dụ Cụ Thể và Giải Thích
Dưới đây là ví dụ cụ thể để minh họa việc tính vận tốc ban đầu:
- Ví dụ 1: Một xe ô tô đang di chuyển với vận tốc 30 m/s và giảm tốc đều với gia tốc -2 m/s2 trong 5 giây. Tính vận tốc ban đầu của xe ô tô.
- Ví dụ 2: Một vật được thả rơi từ độ cao 100 m với vận tốc ban đầu là 0 m/s. Tính vận tốc ban đầu nếu vật rơi xuống mặt đất.
| Thông số | Giá trị |
| Vận tốc cuối (v) | 0 m/s |
| Gia tốc (a) | -2 m/s2 |
| Thời gian (t) | 5 giây |
Sử dụng công thức:
\[ v_0 = v - a \cdot t \] \[ v_0 = 0 - (-2 \cdot 5) = 10 \text{ m/s} \]Vậy vận tốc ban đầu của xe ô tô là 10 m/s.
| Thông số | Giá trị |
| Chiều cao (s) | 100 m |
| Gia tốc trọng trường (g) | 9.8 m/s2 |
| Vận tốc cuối (v) | ? |
Sử dụng công thức:
\[ v = \sqrt{2 \cdot g \cdot s} \] \[ v = \sqrt{2 \cdot 9.8 \cdot 100} = 44.27 \text{ m/s} \]Vậy vận tốc cuối khi vật chạm đất là 44.27 m/s, và vận tốc ban đầu là 0 m/s.
```
3. Phương Pháp Tính Toán Trong Các Tình Huống Khác Nhau
Việc tính toán vận tốc ban đầu có thể được áp dụng trong nhiều tình huống khác nhau, tùy thuộc vào loại chuyển động và các yếu tố ảnh hưởng. Dưới đây là các phương pháp tính toán trong những tình huống phổ biến:
3.1 Vận Tốc Ban Đầu Trong Chuyển Động Thẳng Đều
Trong chuyển động thẳng đều, vật di chuyển với vận tốc không đổi, không có gia tốc. Công thức tính vận tốc ban đầu trong trường hợp này khá đơn giản:
- Công thức: \[ v_0 = v - a \cdot t \] Trong đó, \( v_0 \) là vận tốc ban đầu, \( v \) là vận tốc tại thời điểm t, \( a \) là gia tốc (trong trường hợp này, \( a = 0 \)), và \( t \) là thời gian.
Ví dụ: Một xe đang di chuyển với vận tốc 20 m/s và không thay đổi vận tốc. Nếu cần tính toán vận tốc ban đầu khi thời gian là 0 giây, thì vận tốc ban đầu cũng chính là 20 m/s.
3.2 Vận Tốc Ban Đầu Trong Chuyển Động Có Gia Tốc
Khi vật chuyển động có gia tốc, vận tốc ban đầu có thể được tính dựa trên các yếu tố như vận tốc cuối, gia tốc, và thời gian. Có thể sử dụng công thức sau:
- Công thức: \[ v_0 = v - a \cdot t \] Trong đó, \( v_0 \) là vận tốc ban đầu, \( v \) là vận tốc cuối, \( a \) là gia tốc, và \( t \) là thời gian.
- Hoặc: \[ v_0 = \frac{v - u}{a} \] Trong đó, \( v_0 \) là vận tốc ban đầu, \( v \) là vận tốc cuối, \( u \) là vận tốc đầu, và \( a \) là gia tốc.
Ví dụ: Một vật bắt đầu chuyển động với vận tốc ban đầu không xác định, có gia tốc 3 m/s2 và sau 5 giây đạt được vận tốc 15 m/s. Tính vận tốc ban đầu:
| Thông số | Giá trị |
| Vận tốc cuối (v) | 15 m/s |
| Gia tốc (a) | 3 m/s2 |
| Thời gian (t) | 5 giây |
Sử dụng công thức:
Vậy vận tốc ban đầu của vật là 0 m/s.
3.3 Vận Tốc Ban Đầu Trong Chuyển Động Ném Lên
Trong chuyển động ném lên, vận tốc ban đầu có thể được tính dựa trên chiều cao đạt được hoặc thời gian lên đỉnh. Công thức tính trong trường hợp này là:
- Công thức: \[ v_0 = \sqrt{2 \cdot g \cdot h} \] Trong đó, \( v_0 \) là vận tốc ban đầu, \( g \) là gia tốc trọng trường (9.8 m/s2), và \( h \) là chiều cao đạt được.
Ví dụ: Một vật được ném lên đạt độ cao tối đa 45 m. Tính vận tốc ban đầu của vật:
| Thông số | Giá trị |
| Chiều cao (h) | 45 m |
| Gia tốc trọng trường (g) | 9.8 m/s2 |
Sử dụng công thức:
Vậy vận tốc ban đầu của vật là 30 m/s.

4. Ứng Dụng Thực Tiễn của Vận Tốc Ban Đầu
Vận tốc ban đầu không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tiễn trong đời sống và công việc. Dưới đây là một số ứng dụng nổi bật của vận tốc ban đầu:
4.1 Ứng Dụng Trong Kỹ Thuật và Khoa Học
- Thiết kế Ô Tô: Trong ngành công nghiệp ô tô, việc tính toán vận tốc ban đầu giúp các kỹ sư xác định khả năng tăng tốc và hiệu suất của xe. Ví dụ, khi thiết kế hệ thống phanh, biết được vận tốc ban đầu giúp đảm bảo xe có thể dừng lại an toàn trong khoảng cách mong muốn.
- Khoa Học Vũ Trụ: Vận tốc ban đầu là yếu tố quan trọng trong việc tính toán quỹ đạo của các vệ tinh và tàu vũ trụ. Để đưa vệ tinh vào quỹ đạo chính xác, các nhà khoa học cần tính toán vận tốc ban đầu chính xác khi phóng tên lửa.
- Kỹ Thuật Cơ Khí: Trong thiết kế máy móc và thiết bị, việc hiểu rõ vận tốc ban đầu giúp dự đoán hiệu suất và tuổi thọ của các bộ phận chuyển động. Điều này quan trọng trong việc tối ưu hóa thiết kế và giảm hao mòn.
4.2 Ứng Dụng Trong Cuộc Sống Hàng Ngày
- Chạy Xe và Lái Xe: Khi điều khiển phương tiện, vận tốc ban đầu là thông số quan trọng để tính toán khoảng cách an toàn và thời gian phản ứng trong các tình huống khẩn cấp. Điều này giúp lái xe đưa ra quyết định chính xác hơn để tránh tai nạn.
- Thể Thao: Trong các môn thể thao như bóng đá hoặc bóng rổ, biết được vận tốc ban đầu của quả bóng giúp các huấn luyện viên và vận động viên cải thiện kỹ thuật và chiến thuật. Ví dụ, trong ném bóng rổ, vận tốc ban đầu ảnh hưởng đến độ chính xác của cú ném.
- Thực Nghiệm Vật Lý: Trong các thí nghiệm vật lý, việc đo vận tốc ban đầu của vật thể giúp xác định các yếu tố khác như lực tác động và gia tốc. Điều này rất quan trọng trong nghiên cứu và kiểm chứng các lý thuyết vật lý.

5. Tài Nguyên Học Tập Và Nghiên Cứu Thêm
Để hiểu sâu hơn về tính vận tốc ban đầu và áp dụng nó trong các bài toán vật lý, bạn có thể tham khảo các tài nguyên học tập và nghiên cứu sau đây:
5.1 Sách và Tài Liệu Học Tập
- Sách Giáo Khoa Vật Lý Cơ Bản: Các sách giáo khoa như "Vật Lý 10, 11, 12" thường cung cấp các khái niệm cơ bản về vận tốc ban đầu cùng với các bài tập ví dụ.
- "Principles of Physics" của David Halliday, Robert Resnick và Jearl Walker: Đây là một tài liệu học tập toàn diện về các nguyên lý vật lý, bao gồm cả tính toán vận tốc ban đầu trong các tình huống khác nhau.
- "Fundamentals of Physics" của Richard Wolfson và Jay M. Pasachoff: Cuốn sách này cung cấp các lý thuyết và công thức cơ bản về chuyển động, bao gồm cả vận tốc ban đầu.
5.2 Khóa Học và Nguồn Học Online
- Coursera: Các khóa học như "Introduction to Classical Mechanics" hoặc "Physics: Mechanics" trên Coursera cung cấp kiến thức về chuyển động và vận tốc ban đầu từ các trường đại học hàng đầu.
- Khan Academy: Khan Academy có các bài giảng video miễn phí về cơ học, trong đó bao gồm các bài học về vận tốc, gia tốc và các ứng dụng của vận tốc ban đầu.
- edX: Các khóa học như "Classical Mechanics" trên edX giúp bạn hiểu rõ hơn về các khái niệm vật lý, bao gồm cách tính toán vận tốc ban đầu và các bài toán liên quan.
- MIT OpenCourseWare: MIT OCW cung cấp các khóa học miễn phí về vật lý, trong đó có các bài giảng và tài liệu về tính toán vận tốc ban đầu và các khái niệm liên quan.
XEM THÊM:
6. Câu Hỏi Thường Gặp về Vận Tốc Ban Đầu
Dưới đây là những câu hỏi thường gặp về vận tốc ban đầu cùng với các giải đáp chi tiết để bạn có thể hiểu rõ hơn về khái niệm này:
6.1 Các Thắc Mắc Thường Gặp
- Vận tốc ban đầu là gì? Vận tốc ban đầu là tốc độ mà một vật có khi nó bắt đầu chuyển động. Đây là giá trị của vận tốc tại thời điểm t = 0 trong chuyển động của vật.
- Tại sao vận tốc ban đầu quan trọng trong các bài toán vật lý? Vận tốc ban đầu là yếu tố quan trọng giúp xác định các đặc tính của chuyển động, như gia tốc, thời gian và khoảng cách. Nó là điểm khởi đầu để tính toán các yếu tố khác trong chuyển động.
- Làm thế nào để tính vận tốc ban đầu trong chuyển động có gia tốc? Bạn có thể sử dụng công thức: \[ v_0 = v - a \cdot t \] Trong đó, \( v \) là vận tốc cuối, \( a \) là gia tốc và \( t \) là thời gian. Công thức này giúp tính vận tốc ban đầu dựa trên các yếu tố khác của chuyển động.
6.2 Giải Đáp và Phân Tích
- Ví dụ về vận tốc ban đầu trong cuộc sống thực là gì? Ví dụ, khi một xe ô tô bắt đầu di chuyển từ trạng thái dừng, vận tốc ban đầu của xe là 0 m/s. Nếu xe đã có một vận tốc khi bắt đầu chuyển động, đó là vận tốc ban đầu mà bạn cần tính toán cho các phân tích tiếp theo.
- Làm thế nào để đo vận tốc ban đầu trong thực tế? Vận tốc ban đầu có thể đo bằng cách sử dụng các thiết bị đo lường như đồng hồ bấm giờ và cảm biến tốc độ. Trong thực tế, bạn có thể sử dụng các công cụ và phần mềm hỗ trợ để đo và phân tích vận tốc ban đầu trong các thí nghiệm hoặc bài tập thực tế.
- Có thể áp dụng các công thức tính vận tốc ban đầu trong các bài toán khác nhau không? Có, các công thức tính vận tốc ban đầu có thể áp dụng trong nhiều tình huống khác nhau, từ chuyển động thẳng đều đến chuyển động có gia tốc và ném lên. Việc áp dụng công thức phù hợp giúp giải quyết các bài toán vật lý chính xác và hiệu quả.