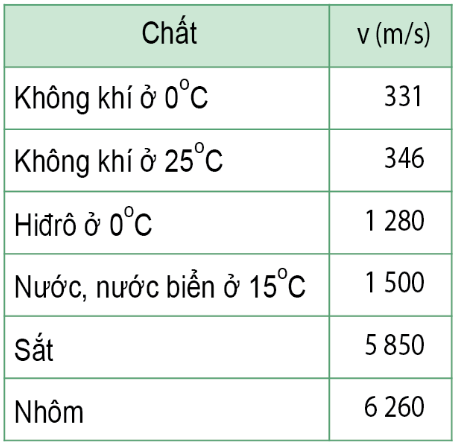
Chủ đề cách tính vận tốc trung bình lớp 10: Cách tính vận tốc trung bình lớp 10 là kiến thức quan trọng trong môn Vật lý, giúp học sinh nắm vững nền tảng chuyển động. Bài viết này sẽ cung cấp hướng dẫn chi tiết, ví dụ minh họa, và giải thích cụ thể, giúp bạn tự tin áp dụng kiến thức vào bài tập và thực tiễn.
Mục lục
Cách Tính Vận Tốc Trung Bình Lớp 10
Vận tốc trung bình là một khái niệm cơ bản trong vật lý lớp 10, liên quan đến sự thay đổi vị trí của một vật trong một khoảng thời gian nhất định. Đây là một phần quan trọng trong chương trình học để hiểu cách mà vật thể chuyển động trong không gian.
Công Thức Tính Vận Tốc Trung Bình
Vận tốc trung bình \(\(V_{tb}\)\) được tính bằng công thức:
Trong đó:
- \(\(V_{tb}\)\): Vận tốc trung bình (m/s)
- \(\(s\)\): Quãng đường đi được (m)
- \(\(t\)\): Thời gian để đi hết quãng đường đó (s)
Ví Dụ Về Bài Tập Tính Vận Tốc Trung Bình
Dưới đây là một ví dụ cụ thể về cách áp dụng công thức tính vận tốc trung bình:
- Một chiếc xe máy chạy trên một quãng đường trong 3 tiếng. Biết 1 tiếng đầu xe chạy với tốc độ trung bình là 50 km/h và 2 giờ sau xe chạy với tốc độ trung bình là 30 km/h. Tính vận tốc trung bình của chiếc xe máy trong suốt quãng thời gian chuyển động?
Giải:
Một Số Lưu Ý Khi Giải Bài Tập
- Luôn đảm bảo rằng đơn vị của các đại lượng như quãng đường, thời gian và vận tốc là thống nhất trước khi áp dụng công thức.
- Chú ý đến các điều kiện đặc biệt của bài toán như vận tốc thay đổi theo từng đoạn hoặc từng thời gian.
- Khi tính toán, cần kiểm tra kết quả để đảm bảo tính chính xác và hợp lý trong bối cảnh thực tế.
Qua việc hiểu và áp dụng đúng công thức tính vận tốc trung bình, học sinh sẽ nắm vững kiến thức cơ bản về chuyển động của vật thể và có thể áp dụng vào nhiều bài toán thực tiễn khác.

.png)
I. Giới thiệu về Vận Tốc Trung Bình
Vận tốc trung bình là một khái niệm cơ bản trong Vật lý lớp 10, giúp chúng ta hiểu rõ hơn về chuyển động của các vật thể. Nó thể hiện sự thay đổi vị trí của một vật theo thời gian và được xác định bằng tỷ số giữa độ dịch chuyển và thời gian dịch chuyển.
- Khái niệm: Vận tốc trung bình là thương số giữa tổng độ dịch chuyển \(\Delta x\) và tổng thời gian dịch chuyển \(\Delta t\).
- Công thức tính: Vận tốc trung bình được tính bằng công thức:
\[
v_{tb} = \frac{\Delta x}{\Delta t}
\]
Trong đó:
- \(\Delta x\) là độ dịch chuyển (khoảng cách thẳng từ điểm đầu đến điểm cuối),
- \(\Delta t\) là thời gian vật thực hiện độ dịch chuyển đó.
- Đơn vị đo: Vận tốc trung bình thường được đo bằng đơn vị m/s (mét trên giây) hoặc km/h (kilômét trên giờ).
Việc hiểu và áp dụng đúng vận tốc trung bình giúp học sinh nắm vững kiến thức về chuyển động, từ đó giải quyết được nhiều bài toán thực tế liên quan đến tốc độ và thời gian.
II. Công Thức Tính Vận Tốc Trung Bình
Vận tốc trung bình là một khái niệm quan trọng trong môn Vật lý, đặc biệt là trong chương trình lớp 10. Dưới đây là cách tính vận tốc trung bình cùng với các ví dụ minh họa để bạn có thể hiểu rõ hơn về khái niệm này.
1. Công Thức Cơ Bản
Vận tốc trung bình (\(v_{tb}\)) được tính bằng công thức:
\[ v_{tb} = \frac{S}{t} \]
Trong đó:
- \(S\) là quãng đường mà vật đã di chuyển (đơn vị: mét, kilomet,...).
- \(t\) là khoảng thời gian mà vật đã di chuyển hết quãng đường đó (đơn vị: giây, giờ,...).
2. Đơn Vị Đo và Cách Chuyển Đổi
Đơn vị của vận tốc trung bình thường là m/s (mét trên giây) hoặc km/h (kilomet trên giờ). Để chuyển đổi giữa hai đơn vị này, ta có thể sử dụng công thức:
\[ 1 \, \text{m/s} = 3.6 \, \text{km/h} \]
Ngược lại, \(1 \, \text{km/h} = \frac{1}{3.6} \, \text{m/s}\).
3. Ví Dụ Minh Họa
Ví dụ 1: Một chiếc ô tô di chuyển quãng đường 180 km trong 3 giờ. Vận tốc trung bình của ô tô là:
\[ v_{tb} = \frac{180 \, \text{km}}{3 \, \text{giờ}} = 60 \, \text{km/h} \]
Ví dụ 2: Một người đi bộ đoạn đường 4 km trong 50 phút. Đổi 50 phút thành giờ:
\[ 50 \, \text{phút} = \frac{50}{60} = \frac{5}{6} \, \text{giờ} \]
Vận tốc trung bình của người đó là:
\[ v_{tb} = \frac{4 \, \text{km}}{\frac{5}{6} \, \text{giờ}} \approx 4.8 \, \text{km/h} \]
Ví dụ 3: Một tàu hỏa di chuyển từ ga A đến ga B với vận tốc 80 km/h trong 2 giờ đầu và 60 km/h trong 1 giờ tiếp theo. Tính vận tốc trung bình của tàu:
Đầu tiên, tính quãng đường trong từng giai đoạn:
- Quãng đường đi trong 2 giờ đầu: \( S_1 = 80 \times 2 = 160 \, \text{km} \)
- Quãng đường đi trong 1 giờ tiếp theo: \( S_2 = 60 \times 1 = 60 \, \text{km} \)
Vận tốc trung bình của tàu trên cả chuyến đi là:
\[ v_{tb} = \frac{S_1 + S_2}{t_1 + t_2} = \frac{160 + 60}{2 + 1} = \frac{220 \, \text{km}}{3 \, \text{giờ}} \approx 73.33 \, \text{km/h} \]

III. Phân Biệt Giữa Vận Tốc Trung Bình và Tốc Độ Trung Bình
Vận tốc trung bình và tốc độ trung bình là hai khái niệm quan trọng trong vật lý, thường dễ gây nhầm lẫn. Tuy nhiên, chúng có sự khác biệt cơ bản về bản chất và cách tính toán.
1. Khái niệm tốc độ trung bình
Tốc độ trung bình là đại lượng vô hướng, dùng để đo lường độ lớn của quãng đường mà một vật di chuyển trong một khoảng thời gian nhất định. Công thức tính tốc độ trung bình được xác định bởi:
\[
v_{\text{tb}} = \frac{\Delta s}{\Delta t}
\]
Trong đó:
- \(\Delta s\) là tổng quãng đường đi được (đơn vị: mét - m).
- \(\Delta t\) là tổng thời gian di chuyển (đơn vị: giây - s).
2. Khái niệm vận tốc trung bình
Vận tốc trung bình là một đại lượng vectơ, không chỉ đo lường tốc độ di chuyển mà còn chỉ hướng di chuyển của vật. Công thức tính vận tốc trung bình là:
\[
\vec{v}_{\text{tb}} = \frac{\Delta \vec{x}}{\Delta t}
\]
Trong đó:
- \(\Delta \vec{x}\) là độ dời - khoảng cách giữa vị trí cuối và vị trí đầu theo một hướng nhất định (đơn vị: mét - m).
- \(\Delta t\) là thời gian di chuyển (đơn vị: giây - s).
Do đó, vận tốc trung bình phụ thuộc vào hướng di chuyển và có thể có giá trị âm nếu vật di chuyển ngược lại so với hướng ban đầu.
3. Sự khác biệt giữa vận tốc và tốc độ trung bình
Khác biệt chính giữa hai đại lượng này nằm ở tính chất vectơ của vận tốc và vô hướng của tốc độ:
- Tốc độ trung bình chỉ đo lường độ lớn của quãng đường di chuyển mà không quan tâm đến hướng, do đó luôn có giá trị dương.
- Vận tốc trung bình có tính đến hướng, do đó có thể dương, âm hoặc bằng không tùy thuộc vào hướng và độ dời của chuyển động.
4. Ứng dụng thực tế
Trong thực tế, việc phân biệt giữa vận tốc trung bình và tốc độ trung bình rất quan trọng. Ví dụ, trong giao thông, tốc độ trung bình giúp đánh giá hiệu suất di chuyển của phương tiện, trong khi vận tốc trung bình có thể được sử dụng để xác định hướng di chuyển của một vật thể trong không gian.
Nắm vững sự khác biệt này sẽ giúp bạn giải quyết các bài toán vật lý liên quan một cách chính xác và hiệu quả.

IV. Các Dạng Bài Tập Liên Quan
Dưới đây là các dạng bài tập phổ biến liên quan đến vận tốc trung bình trong chương trình Vật lý lớp 10. Các bài tập này sẽ giúp bạn củng cố kiến thức và áp dụng công thức tính vận tốc trung bình vào các tình huống thực tế.
1. Bài Tập Cơ Bản
- Dạng 1: Tính vận tốc trung bình khi biết quãng đường và thời gian.
- Dạng 2: Tính quãng đường khi biết vận tốc trung bình và thời gian.
- Dạng 3: Tính thời gian khi biết vận tốc trung bình và quãng đường.
Ví dụ: Một ô tô di chuyển từ điểm A đến điểm B, quãng đường là 120 km và thời gian đi hết là 2 giờ. Tính vận tốc trung bình của ô tô.
Giải: Áp dụng công thức \(v = \frac{S}{t} = \frac{120 \text{ km}}{2 \text{ giờ}} = 60 \text{ km/h}\).
Ví dụ: Một người đi bộ với vận tốc trung bình là 5 km/h trong 3 giờ. Tính quãng đường người đó đã đi.
Giải: Áp dụng công thức \(S = v \times t = 5 \text{ km/h} \times 3 \text{ giờ} = 15 \text{ km}\).
Ví dụ: Một tàu hỏa đi với vận tốc trung bình là 80 km/h và quãng đường là 240 km. Tính thời gian tàu di chuyển.
Giải: Áp dụng công thức \(t = \frac{S}{v} = \frac{240 \text{ km}}{80 \text{ km/h}} = 3 \text{ giờ}\).
2. Bài Tập Nâng Cao
- Dạng 1: Tính vận tốc trung bình khi quãng đường được chia thành nhiều đoạn với các vận tốc khác nhau.
- Dạng 2: Tính vận tốc trung bình khi thời gian di chuyển trên mỗi đoạn đường là khác nhau.
Ví dụ: Một xe máy đi từ A đến B với vận tốc 30 km/h trên nửa đoạn đường đầu và 60 km/h trên nửa đoạn đường sau. Tính vận tốc trung bình trên toàn bộ quãng đường.
Giải: Áp dụng công thức:
\[
v_{\text{tb}} = \frac{2 \times v_1 \times v_2}{v_1 + v_2} = \frac{2 \times 30 \times 60}{30 + 60} = 40 \text{ km/h}
\]
Ví dụ: Một xe ô tô đi nửa thời gian đầu với vận tốc 50 km/h và nửa thời gian còn lại với vận tốc 100 km/h. Tính vận tốc trung bình trên toàn bộ thời gian di chuyển.
Giải: Áp dụng công thức:
\[
v_{\text{tb}} = \frac{S_1 + S_2}{t_1 + t_2} = \frac{50t + 100t}{t + t} = 75 \text{ km/h}
\]
3. Bài Tập Tổng Hợp
- Bài tập tổng hợp sẽ yêu cầu tính toán và kết hợp các kiến thức về vận tốc trung bình, quãng đường và thời gian trong nhiều tình huống thực tế khác nhau.
Ví dụ: Một người lái xe từ A đến B với các vận tốc khác nhau ở từng chặng. Sau khi tính toán, bạn có thể so sánh các kết quả để hiểu rõ hơn về ảnh hưởng của các yếu tố này đến vận tốc trung bình.

V. Các Lưu Ý Quan Trọng Khi Giải Bài Tập
Khi giải bài tập về vận tốc trung bình, học sinh cần chú ý một số điểm quan trọng sau để tránh các sai sót phổ biến và đạt kết quả chính xác:
1. Hiểu rõ yêu cầu của đề bài
Trước khi bắt đầu giải, bạn cần đọc kỹ đề bài để xác định chính xác yêu cầu. Đặc biệt, cần phân biệt rõ ràng giữa vận tốc trung bình và tốc độ trung bình, hai khái niệm này dễ gây nhầm lẫn.
2. Sử dụng đúng công thức
Hãy chắc chắn rằng bạn sử dụng đúng công thức tính vận tốc trung bình:
- Nếu đề bài cho quãng đường và thời gian: \[v_{tb} = \frac{S}{t}\]
- Nếu bài toán yêu cầu tính vận tốc trung bình dựa trên nhiều đoạn đường hoặc nhiều thời gian khác nhau: \[v_{tb} = \frac{S_1 + S_2 + \dots + S_n}{t_1 + t_2 + \dots + t_n}\]
3. Chú ý đơn vị đo
Đảm bảo rằng tất cả các giá trị bạn sử dụng trong công thức đều đồng nhất về đơn vị. Ví dụ, quãng đường phải cùng đơn vị với thời gian tương ứng (km và giờ, hoặc mét và giây).
4. Xử lý các trường hợp đặc biệt
Khi giải các bài toán có nhiều giai đoạn chuyển động với các tốc độ khác nhau, hãy cẩn thận tính riêng từng đoạn đường và thời gian trước khi cộng lại để tính vận tốc trung bình.
5. Tránh các lỗi tính toán cơ bản
Một trong những lỗi phổ biến là tính sai kết quả do tính nhầm hoặc thiếu chính xác trong các bước trung gian. Do đó, cần kiểm tra lại các phép tính trước khi kết luận.
6. Sử dụng phương pháp giải bài hiệu quả
Phương pháp tốt nhất là vẽ sơ đồ mô phỏng chuyển động để dễ dàng hình dung và phân tích bài toán. Điều này giúp bạn theo dõi quá trình giải một cách rõ ràng và tránh bỏ sót thông tin quan trọng.
7. Ghi nhớ công thức qua các mẹo
Hãy luyện tập thường xuyên và sử dụng các mẹo ghi nhớ như công thức viết tắt, hoặc hình ảnh hóa các công thức, để dễ dàng áp dụng khi làm bài tập.
XEM THÊM:
VI. Tổng Kết và Củng Cố Kiến Thức
Để nắm vững kiến thức về vận tốc trung bình, học sinh cần tổng hợp lại những nội dung đã học và áp dụng chúng vào thực tế. Dưới đây là các bước tổng kết và củng cố kiến thức quan trọng:
1. Ôn tập lý thuyết
- Học sinh cần nhớ lại định nghĩa và công thức tính vận tốc trung bình \(v_{\text{tb}} = \frac{S}{t}\), trong đó \(S\) là quãng đường và \(t\) là thời gian di chuyển.
- Nhớ lại các đơn vị đo lường và cách chuyển đổi giữa các đơn vị như m/s, km/h, và cm/s.
- Phân biệt rõ ràng giữa vận tốc trung bình và tốc độ trung bình để tránh nhầm lẫn trong quá trình giải bài tập.
2. Củng cố qua bài tập thực hành
Bài tập là công cụ hữu ích để củng cố kiến thức và phát triển kỹ năng giải quyết vấn đề:
- Bài tập tính vận tốc trung bình trong các trường hợp chuyển động thẳng đều và không đều.
- Bài tập vẽ và phân tích đồ thị quãng đường - thời gian và vận tốc - thời gian.
- Giải bài tập liên quan đến các tình huống thực tế như chuyển động của xe cộ, máy bay, hay vận động viên để hiểu rõ hơn về ứng dụng của vận tốc trung bình.
3. Ứng dụng trong các môn học khác
Vận tốc trung bình không chỉ quan trọng trong môn Vật lý mà còn có thể liên quan đến nhiều lĩnh vực khác như:
- Toán học: Liên quan đến việc giải các phương trình và đồ thị.
- Địa lý: Ứng dụng trong việc tính toán thời gian và quãng đường di chuyển trong các bài học về địa lý địa hình.
- Hóa học: Sử dụng để mô tả tốc độ phản ứng trong một số thí nghiệm.
Cuối cùng, hãy chắc chắn rằng bạn đã nắm vững các kiến thức cơ bản và sẵn sàng áp dụng chúng vào các tình huống khác nhau. Điều này không chỉ giúp bạn đạt kết quả tốt trong môn học mà còn trang bị cho bạn kỹ năng giải quyết vấn đề trong cuộc sống hàng ngày.