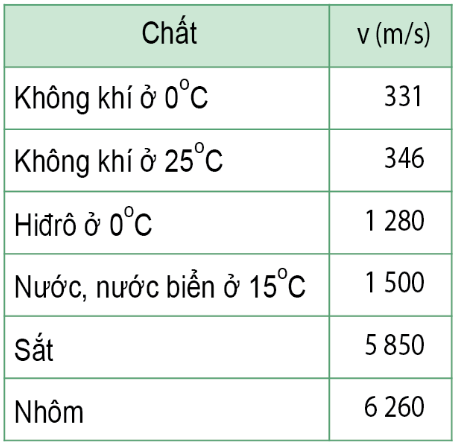
Chủ đề cách tính vận tốc trung bình lớp 5: Cách tính vận tốc trung bình lớp 5 là một kiến thức quan trọng giúp học sinh nắm vững khái niệm cơ bản về vận tốc. Trong bài viết này, chúng tôi sẽ hướng dẫn chi tiết cách tính vận tốc trung bình qua các ví dụ minh họa và bài tập thực hành, giúp các em học sinh hiểu rõ và áp dụng hiệu quả vào các bài toán thực tế.
Mục lục
Cách Tính Vận Tốc Trung Bình Lớp 5
Vận tốc trung bình là một kiến thức cơ bản trong chương trình học toán lớp 5, giúp học sinh hiểu rõ về khái niệm vận tốc và cách tính toán vận tốc trung bình khi di chuyển trong các quãng đường khác nhau. Công thức tính vận tốc trung bình được áp dụng trong nhiều bài tập thực tế, giúp các em rèn luyện kỹ năng giải toán một cách hiệu quả.
1. Khái Niệm Vận Tốc Trung Bình
Vận tốc trung bình là đại lượng đo lường tốc độ di chuyển của một vật thể trong một khoảng thời gian nhất định. Công thức tổng quát để tính vận tốc trung bình là:
\[
v_{tb} = \frac{S}{t}
\]
Trong đó:
- \(v_{tb}\) là vận tốc trung bình.
- \(S\) là quãng đường di chuyển.
- \(t\) là thời gian di chuyển.
2. Công Thức Tính Vận Tốc Trung Bình Khi Di Chuyển Qua Nhiều Quãng Đường
Khi vật thể di chuyển qua nhiều quãng đường với các vận tốc khác nhau, vận tốc trung bình được tính bằng cách lấy tổng các quãng đường chia cho tổng thời gian di chuyển:
\[
v_{tb} = \frac{d_1 + d_2 + \dots + d_n}{t_1 + t_2 + \dots + t_n}
\]
Trong đó:
- \(d_1, d_2, \dots, d_n\) là các quãng đường đi được.
- \(t_1, t_2, \dots, t_n\) là thời gian tương ứng để đi các quãng đường đó.
3. Ví Dụ Minh Họa
Giả sử một chiếc ô tô đi từ điểm A đến điểm B với vận tốc 60 km/h trong quãng đường 200 km, sau đó đi từ điểm B đến điểm C với vận tốc 80 km/h trong quãng đường 300 km. Vận tốc trung bình trên cả quãng đường AB và BC sẽ được tính như sau:
\[
v_{tb} = \frac{200 \, \text{km} + 300 \, \text{km}}{\frac{200 \, \text{km}}{60 \, \text{km/h}} + \frac{300 \, \text{km}}{80 \, \text{km/h}}} \approx 67.27 \, \text{km/h}
\]
4. Ứng Dụng Thực Tế Của Vận Tốc Trung Bình
Kiến thức về vận tốc trung bình không chỉ hữu ích trong học tập mà còn trong đời sống hàng ngày. Học sinh có thể áp dụng kiến thức này để tính toán thời gian cần thiết để di chuyển trên các quãng đường khác nhau, giúp lập kế hoạch cho các chuyến đi, và hiểu rõ hơn về chuyển động trong tự nhiên.
5. Các Bài Tập Vận Dụng
Để rèn luyện kỹ năng tính toán vận tốc trung bình, học sinh có thể thực hành với các bài tập như:
- Bài tập tính vận tốc trung bình khi biết quãng đường và thời gian.
- Bài tập tính vận tốc trung bình trong các trường hợp chuyển động ngược chiều và cùng chiều.
- Bài tập tính vận tốc trung bình khi vật thể chuyển động với các vận tốc khác nhau trên các quãng đường khác nhau.
Các bài tập này giúp học sinh củng cố kiến thức, đồng thời phát triển khả năng tư duy và giải quyết vấn đề trong toán học.
6. Lời Kết
Việc nắm vững cách tính vận tốc trung bình là nền tảng quan trọng trong quá trình học tập môn toán và lý, đồng thời là kỹ năng cần thiết trong nhiều lĩnh vực khác nhau. Hy vọng với những kiến thức đã được chia sẻ, các em học sinh sẽ học tốt hơn và áp dụng được vào thực tế cuộc sống.

.png)
2. Công Thức Tính Vận Tốc Trung Bình
Công thức tính vận tốc trung bình là một trong những kiến thức cơ bản trong chương trình lớp 5, giúp học sinh hiểu cách đo lường tốc độ di chuyển của một vật thể. Vận tốc trung bình được tính bằng cách chia quãng đường đi được cho thời gian thực hiện hành trình đó.
Công thức tổng quát để tính vận tốc trung bình như sau:
\[ V_{\text{tb}} = \frac{S}{t} \]
- Trong đó:
- \( V_{\text{tb}} \) là vận tốc trung bình.
- \( S \) là quãng đường đã đi được.
- \( t \) là thời gian để đi hết quãng đường đó.
Ví dụ: Một chiếc xe di chuyển 120 km trong 3 giờ. Vận tốc trung bình của xe là:
\[ V_{\text{tb}} = \frac{120 \, \text{km}}{3 \, \text{giờ}} = 40 \, \text{km/h} \]
Điều này có nghĩa là trung bình trong mỗi giờ, chiếc xe đã đi được 40 km.
3. Ứng Dụng Của Vận Tốc Trung Bình
Vận tốc trung bình không chỉ là một khái niệm lý thuyết mà còn có nhiều ứng dụng thực tế trong đời sống hàng ngày. Dưới đây là một số ví dụ về cách vận tốc trung bình được sử dụng:
- Tính toán thời gian di chuyển: Vận tốc trung bình giúp chúng ta ước lượng thời gian cần thiết để di chuyển từ điểm này đến điểm khác. Ví dụ, nếu biết vận tốc trung bình của một chiếc xe là 60 km/h, chúng ta có thể dễ dàng tính toán thời gian cần thiết để đi từ thành phố A đến thành phố B cách nhau 180 km.
- Đánh giá hiệu suất: Vận tốc trung bình cũng được sử dụng để đánh giá hiệu suất hoạt động của các phương tiện giao thông. Các nhà sản xuất xe có thể sử dụng vận tốc trung bình để xác định mức tiêu thụ nhiên liệu và các chỉ số hiệu suất khác.
- Quản lý giao thông: Trong quy hoạch và quản lý giao thông, vận tốc trung bình của các phương tiện trên các tuyến đường giúp nhà quản lý xác định được những điểm nóng về ùn tắc giao thông, từ đó đưa ra các giải pháp cải thiện hiệu quả.
- Ứng dụng trong thể thao: Trong các môn thể thao như chạy đua hoặc đua xe, vận tốc trung bình của vận động viên hoặc xe đua được sử dụng để đánh giá chiến thuật và hiệu suất, cũng như để so sánh với các đối thủ.
Vận tốc trung bình là một công cụ hữu ích không chỉ trong học tập mà còn trong nhiều khía cạnh của cuộc sống và công việc hàng ngày.

4. Các Bài Tập Thực Hành Về Vận Tốc Trung Bình
Dưới đây là các bài tập thực hành về cách tính vận tốc trung bình cho học sinh lớp 5. Các bài tập này được thiết kế để giúp học sinh nắm vững kiến thức về vận tốc trung bình thông qua việc thực hành tính toán trong nhiều tình huống khác nhau.
4.1 Bài tập cơ bản
- Bài tập 1: Một học sinh đi bộ từ nhà đến trường với quãng đường dài 2 km trong 30 phút. Tính vận tốc trung bình của học sinh đó. \[ v = \frac{s}{t} = \frac{2 \text{ km}}{30 \text{ phút}} = \frac{2000 \text{ m}}{1800 \text{ giây}} = 1.11 \text{ m/s} \]
- Bài tập 2: Một chiếc xe đạp di chuyển trên quãng đường 10 km trong 25 phút. Hãy tính vận tốc trung bình của chiếc xe đạp. \[ v = \frac{s}{t} = \frac{10 \text{ km}}{25 \text{ phút}} = \frac{10000 \text{ m}}{1500 \text{ giây}} = 6.67 \text{ m/s} \]
4.2 Bài tập nâng cao
- Bài tập 3: Một người chạy bộ trên hai quãng đường liên tiếp: quãng đường đầu dài 3 km trong 20 phút và quãng đường thứ hai dài 2 km trong 15 phút. Tính vận tốc trung bình trên toàn bộ quãng đường. \[ v = \frac{s_{1} + s_{2}}{t_{1} + t_{2}} = \frac{3 \text{ km} + 2 \text{ km}}{20 \text{ phút} + 15 \text{ phút}} = \frac{5 \text{ km}}{35 \text{ phút}} = \frac{5000 \text{ m}}{2100 \text{ giây}} \approx 2.38 \text{ m/s} \]
- Bài tập 4: Một xe ô tô đi từ điểm A đến điểm B, quãng đường đầu tiên dài 50 km với vận tốc trung bình 60 km/h, quãng đường thứ hai dài 30 km với vận tốc trung bình 40 km/h. Tính vận tốc trung bình trên cả hành trình. \[ v = \frac{s_{1} + s_{2}}{t_{1} + t_{2}} = \frac{50 \text{ km} + 30 \text{ km}}{\frac{50 \text{ km}}{60 \text{ km/h}} + \frac{30 \text{ km}}{40 \text{ km/h}}} = \frac{80 \text{ km}}{\frac{5}{6} \text{ h} + \frac{3}{4} \text{ h}} \approx 50.77 \text{ km/h} \]
4.3 Bài tập thực tế
- Bài tập 5: Một người đi xe máy từ nhà đến công ty qua ba đoạn đường: 5 km đầu với vận tốc 40 km/h, 10 km tiếp theo với vận tốc 50 km/h, và 15 km cuối với vận tốc 60 km/h. Hãy tính vận tốc trung bình trên cả hành trình. \[ v = \frac{s_{1} + s_{2} + s_{3}}{t_{1} + t_{2} + t_{3}} = \frac{5 \text{ km} + 10 \text{ km} + 15 \text{ km}}{\frac{5 \text{ km}}{40 \text{ km/h}} + \frac{10 \text{ km}}{50 \text{ km/h}} + \frac{15 \text{ km}}{60 \text{ km/h}}} \approx 52.17 \text{ km/h} \]
- Bài tập 6: Một học sinh chạy 4 vòng quanh sân trường, mỗi vòng dài 400 m, với thời gian mỗi vòng lần lượt là 80 giây, 85 giây, 90 giây, và 95 giây. Tính vận tốc trung bình của học sinh đó. \[ v = \frac{4 \times 400 \text{ m}}{80 \text{ giây} + 85 \text{ giây} + 90 \text{ giây} + 95 \text{ giây}} = \frac{1600 \text{ m}}{350 \text{ giây}} \approx 4.57 \text{ m/s} \]

5. Các Lỗi Thường Gặp Khi Tính Vận Tốc Trung Bình
Khi học sinh thực hiện các bài toán về tính vận tốc trung bình, có một số lỗi phổ biến mà các em thường gặp phải. Dưới đây là danh sách các lỗi đó và cách khắc phục chúng một cách hiệu quả.
- Lỗi 1: Sử dụng sai công thức tính vận tốc trung bình
Nhiều học sinh nhầm lẫn giữa vận tốc trung bình với giá trị trung bình của vận tốc. Công thức đúng để tính vận tốc trung bình là:
\[ v_{trung\ bình} = \frac{S_{1} + S_{2} + \dots + S_{n}}{t_{1} + t_{2} + \dots + t_{n}} \]Trong khi đó, giá trị trung bình của vận tốc lại được tính bằng:
\[ v_{trung\ bình} = \frac{v_{1} + v_{2} + \dots + v_{n}}{n} \]Do đó, các em cần chú ý sử dụng đúng công thức cho từng loại bài toán.
- Lỗi 2: Đổi đơn vị không chính xác
Một lỗi phổ biến khác là các em không đổi đơn vị thời gian và quãng đường sao cho đồng nhất trước khi tính toán. Ví dụ, quãng đường có thể đo bằng kilômét (km), trong khi thời gian có thể tính bằng phút hoặc giờ. Do đó, cần đổi thời gian ra giờ trước khi áp dụng công thức:
\[ v = \frac{S}{t} \] - Lỗi 3: Nhầm lẫn khi tính tổng quãng đường và tổng thời gian
Khi bài toán yêu cầu tính vận tốc trung bình cho nhiều chặng đường khác nhau, học sinh thường quên cộng tổng tất cả các quãng đường và thời gian lại trước khi tính. Công thức chính xác là:
\[ v_{trung\ bình} = \frac{\sum S_{i}}{\sum t_{i}} \]Nếu không cộng tất cả các giá trị lại, kết quả sẽ sai.
- Lỗi 4: Không nhận biết được điều kiện bài toán
Một số bài toán yêu cầu tính vận tốc trung bình trên các đoạn đường khác nhau nhưng không cùng điều kiện (ví dụ, một đoạn đường lên dốc và một đoạn đường xuống dốc). Các em cần chú ý rằng vận tốc trung bình không chỉ đơn giản là trung bình cộng của các vận tốc trên các đoạn đường mà phải tính theo tổng quãng đường và tổng thời gian.
- Lỗi 5: Bẫy bài toán liên quan đến vận tốc
Các bài toán thường đưa ra các bẫy như sử dụng vận tốc ở một chiều để suy ra vận tốc trung bình cho toàn bộ quãng đường mà không tính toán kỹ. Học sinh cần đọc kỹ đề bài và sử dụng công thức một cách cẩn thận để tránh các bẫy này.
Bằng cách nhận biết và tránh những lỗi trên, các em học sinh sẽ cải thiện đáng kể khả năng tính toán và giải quyết các bài toán vận tốc trung bình một cách chính xác hơn.

6. Lời Khuyên Từ Giáo Viên
Để tính toán vận tốc trung bình một cách chính xác và hiệu quả, giáo viên thường đưa ra một số lời khuyên hữu ích như sau:
- Nắm vững công thức cơ bản: Trước tiên, học sinh cần nhớ rõ công thức tính vận tốc trung bình: \[ v_{\text{tb}} = \frac{s_1 + s_2 + ... + s_n}{t_1 + t_2 + ... + t_n} \] Trong đó \( s \) là quãng đường và \( t \) là thời gian. Công thức này cần được áp dụng một cách linh hoạt tùy vào bài toán cụ thể.
- Chú ý đến đơn vị đo: Khi giải các bài toán, cần đảm bảo rằng các đơn vị đo (quãng đường, thời gian) phải nhất quán. Ví dụ, nếu quãng đường được tính bằng kilômét (km) thì thời gian phải được chuyển đổi về giờ (h) hoặc phút (min).
- Phân tích đề bài cẩn thận: Trước khi bắt tay vào giải, hãy đọc kỹ đề bài để hiểu rõ yêu cầu và phân tích từng bước nhỏ, như tính quãng đường từng đoạn, thời gian di chuyển, v.v. Điều này giúp tránh nhầm lẫn trong quá trình tính toán.
- Luyện tập thường xuyên: Học sinh nên làm nhiều bài tập để quen với việc tính vận tốc trung bình. Việc này giúp củng cố kiến thức và nâng cao kỹ năng giải toán.
- Tham khảo ý kiến giáo viên: Khi gặp khó khăn, đừng ngần ngại hỏi giáo viên để được hướng dẫn cụ thể hơn. Giáo viên sẽ giúp học sinh hiểu rõ những khía cạnh phức tạp và đưa ra những mẹo hữu ích.
Với những lời khuyên trên, học sinh sẽ có thể tính toán vận tốc trung bình một cách chính xác và tự tin hơn trong các bài kiểm tra và thi cử.