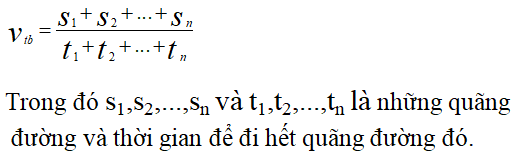Muốn Tính Vận Tốc: Công Thức, Cách Tính và Ví Dụ Minh Họa

Vận tốc là một đại lượng vật lý quan trọng, thường được sử dụng để mô tả tốc độ di chuyển của một vật thể. Dưới đây là một số công thức và phương pháp tính vận tốc cơ bản.

1. Vận tốc trung bình

Vận tốc trung bình của một vật thể được tính bằng công thức:

\[
V_{tb} = \frac{S}{t}
\]
Trong đó:

• \( V_{tb} \): Vận tốc trung bình
• \( S \): Quãng đường đã đi
• \( t \): Thời gian đi quãng đường đó

2. Vận tốc tức thời

Vận tốc tức thời mô tả tốc độ và hướng di chuyển của một vật tại một thời điểm cụ thể trên quỹ đạo của nó. Công thức tính vận tốc tức thời là:

\[
v = \frac{\Delta s}{\Delta t}
\]
Trong đó:

• \( v \): Vận tốc tức thời
• \( \Delta s \): Quãng đường nhỏ mà vật đi được trong khoảng thời gian rất ngắn \( \Delta t \)
• \( \Delta t \): Khoảng thời gian rất ngắn

3. Vận tốc trong chuyển động thẳng đều

Trong chuyển động thẳng đều, vận tốc được tính theo công thức:

\[
v = \frac{S}{t}
\]
Công thức này đơn giản và trực quan, bởi vì trong chuyển động thẳng đều, tốc độ không đổi và thời gian di chuyển tỷ lệ thuận với quãng đường đi được.

4. Vận tốc trong chuyển động biến đổi đều

Đối với chuyển động biến đổi đều, công thức tính vận tốc có thể được biểu diễn như sau:

\[
v = v_0 + at
\]
Trong đó:

• \( v \): Vận tốc tại thời điểm \( t \)
• \( v_0 \): Vận tốc ban đầu
• \( a \): Gia tốc

5. Bài tập vận dụng

• Bài tập 1: Một xe máy di chuyển quãng đường 90 km trong 2 giờ. Tính vận tốc trung bình của xe.
• Bài tập 2: Một máy bay bay từ Hà Nội đến TP.HCM, quãng đường là 1500 km, trong 3 giờ 45 phút. Tính vận tốc trung bình của máy bay.
• Bài tập 3: Một ô tô tăng tốc từ 0 đến 60 km/h trong 10 giây. Tính vận tốc tức thời của ô tô tại thời điểm cuối.

Kết luận

Việc hiểu và áp dụng đúng các công thức tính vận tốc giúp chúng ta giải quyết hiệu quả các bài toán trong thực tế, cũng như trong học tập. Các công thức này không chỉ quan trọng trong môn Vật lý mà còn ứng dụng rộng rãi trong đời sống hàng ngày.

Vận tốc là đại lượng vật lý mô tả sự thay đổi vị trí của một vật thể trong một khoảng thời gian. Vận tốc không chỉ bao gồm độ lớn mà còn bao gồm hướng của chuyển động. Vận tốc thường được ký hiệu là \( v \) và được đo bằng đơn vị mét trên giây \((m/s)\) hoặc kilômét trên giờ \((km/h)\).

Công thức tính vận tốc cho chuyển động thẳng đều được biểu diễn dưới dạng:

Trong đó:

• \( v \): Vận tốc
• \( s \): Quãng đường di chuyển
• \( t \): Thời gian di chuyển

Vận tốc có thể được chia thành hai loại chính:

1. Vận tốc trung bình: Là vận tốc được tính bằng cách chia tổng quãng đường di chuyển cho tổng thời gian di chuyển, công thức là: \[ v_{\text{tb}} = \frac{s_{\text{tổng}}}{t_{\text{tổng}}} \]
2. Vận tốc tức thời: Là vận tốc tại một thời điểm cụ thể hoặc tại một vị trí cụ thể trong quá trình chuyển động.

Đơn vị vận tốc phụ thuộc vào đơn vị của quãng đường và thời gian. Các đơn vị phổ biến bao gồm:

• \( m/s \) (mét trên giây)
• \( km/h \) (kilômét trên giờ)

Vận tốc không chỉ đơn thuần là tốc độ di chuyển mà còn thể hiện hướng di chuyển, làm cho nó khác biệt với khái niệm "tốc độ" chỉ bao gồm độ lớn mà không quan tâm đến hướng.

Để tính vận tốc trong chuyển động, chúng ta áp dụng công thức cơ bản:

Trong đó:

• \( v \): Vận tốc của vật (mét trên giây \((m/s)\) hoặc kilômét trên giờ \((km/h)\))
• \( s \): Quãng đường mà vật đã di chuyển (mét \((m)\) hoặc kilômét \((km)\))
• \( t \): Thời gian di chuyển của vật (giây \((s)\) hoặc giờ \((h)\))

Công thức này áp dụng cho chuyển động thẳng đều, khi vận tốc của vật không đổi theo thời gian. Tuy nhiên, trong trường hợp vật có sự thay đổi về vận tốc, chúng ta có thể tính vận tốc trung bình bằng công thức:

Trong đó:

• \( v_{\text{tb}} \): Vận tốc trung bình
• \( s_{\text{tổng}} \): Tổng quãng đường di chuyển
• \( t_{\text{tổng}} \): Tổng thời gian di chuyển

Ngoài ra, nếu xét đến các trường hợp chuyển động không đều, vận tốc tức thời \( v_{\text{tt}} \) tại một thời điểm nhất định có thể được xác định bằng công thức đạo hàm:

Trong đó:

• \( ds \): Một thay đổi rất nhỏ của quãng đường
• \( dt \): Một thay đổi rất nhỏ của thời gian

Với các bài toán thực tế, chúng ta thường sử dụng các đơn vị tiêu chuẩn như:

• Vận tốc trong đơn vị \( m/s \) để tính toán cho các bài toán vật lý thông thường
• Vận tốc trong đơn vị \( km/h \) để tính toán trong các tình huống giao thông

Để hiểu rõ hơn về cách tính vận tốc, chúng ta sẽ cùng giải quyết một số bài tập vận dụng cụ thể. Các bài tập này sẽ giúp bạn nắm vững công thức tính vận tốc và áp dụng vào các tình huống thực tế.

1. Bài tập 1: Một xe ô tô đi từ điểm A đến điểm B với quãng đường dài 120 km trong thời gian 2 giờ. Tính vận tốc của xe ô tô.

Giải:

• Quãng đường \( s = 120 \, km \)
• Thời gian \( t = 2 \, giờ \)
• Vận tốc của xe ô tô \( v = \frac{s}{t} = \frac{120}{2} = 60 \, km/h \)
2. Bài tập 2: Một người chạy trên quãng đường dài 400 mét trong 50 giây. Tính vận tốc trung bình của người đó.

Giải:

• Quãng đường \( s = 400 \, m \)
• Thời gian \( t = 50 \, s \)
• Vận tốc trung bình \( v_{\text{tb}} = \frac{s}{t} = \frac{400}{50} = 8 \, m/s \)
3. Bài tập 3: Một máy bay bay với vận tốc \( 800 \, km/h \) trong thời gian 3 giờ. Tính quãng đường mà máy bay đã di chuyển.

Giải:

• Vận tốc \( v = 800 \, km/h \)
• Thời gian \( t = 3 \, giờ \)
• Quãng đường \( s = v \times t = 800 \times 3 = 2400 \, km \)

Các bài tập trên giúp bạn rèn luyện kỹ năng tính toán vận tốc, quãng đường và thời gian trong các tình huống thực tế. Hãy luyện tập thường xuyên để nắm vững kiến thức này!

Vận tốc đóng vai trò rất quan trọng trong nhiều lĩnh vực đời sống và khoa học. Dưới đây là một số ứng dụng tiêu biểu của vận tốc trong thực tế:

1. Giao thông và vận tải:

   Vận tốc được sử dụng để đánh giá tốc độ di chuyển của các phương tiện như ô tô, xe máy, tàu hỏa, máy bay,... Tính toán vận tốc giúp tối ưu hóa thời gian di chuyển, đảm bảo an toàn giao thông và thiết kế các hệ thống vận tải hiệu quả hơn.

2. Thể thao:

   Trong các môn thể thao như chạy bộ, đua xe đạp, bơi lội,... vận tốc của vận động viên đóng vai trò quyết định trong thành tích thi đấu. Tính toán vận tốc giúp huấn luyện viên điều chỉnh phương pháp tập luyện và chiến thuật phù hợp để đạt được kết quả tốt nhất.

3. Công nghiệp:

   Trong sản xuất và công nghiệp, vận tốc của các máy móc và thiết bị ảnh hưởng đến hiệu suất làm việc và năng suất. Ví dụ, vận tốc của băng chuyền trong dây chuyền sản xuất cần được điều chỉnh phù hợp để đảm bảo quá trình sản xuất diễn ra liên tục và hiệu quả.

4. Thiên văn học:

   Trong lĩnh vực thiên văn học, vận tốc được sử dụng để đo lường sự di chuyển của các hành tinh, ngôi sao, và thiên thể khác. Từ đó, các nhà khoa học có thể dự đoán quỹ đạo, thời gian quay, và nghiên cứu về vũ trụ.

5. Khoa học y tế:

   Trong y học, vận tốc dòng máu trong cơ thể được theo dõi để đánh giá sức khỏe của tim mạch và các cơ quan khác. Sử dụng các thiết bị hiện đại như máy siêu âm Doppler, các bác sĩ có thể kiểm tra vận tốc dòng chảy của máu và phát hiện các bất thường.

Như vậy, vận tốc không chỉ là một khái niệm trong vật lý mà còn là một yếu tố quan trọng trong nhiều lĩnh vực khác nhau. Hiểu và áp dụng vận tốc đúng cách giúp nâng cao hiệu quả trong công việc và đời sống.

Vận tốc là một đại lượng cơ bản trong vật lý, nhưng để tính toán chính xác và áp dụng vào các tình huống phức tạp, chúng ta cần xem xét một số công thức liên quan khác. Dưới đây là các công thức mở rộng có liên hệ trực tiếp với vận tốc:

1. Công thức tính gia tốc:

   Gia tốc \((a)\) là sự thay đổi của vận tốc trong một khoảng thời gian nhất định. Công thức tính gia tốc được biểu diễn như sau:

   \[ a = \frac{{\Delta v}}{{\Delta t}} \]

   Trong đó:

   • \(a\): Gia tốc (m/s²)
   • \(\Delta v\): Sự thay đổi vận tốc (m/s)
   • \(\Delta t\): Khoảng thời gian (s)
2. Công thức quãng đường trong chuyển động thẳng đều:

   Trong chuyển động thẳng đều, quãng đường \((s)\) được tính theo công thức:

   \[ s = v \cdot t \]

   Trong đó:

   • \(s\): Quãng đường (m)
   • \(v\): Vận tốc (m/s)
   • \(t\): Thời gian (s)
3. Công thức động năng:

   Động năng \((K)\) của một vật chuyển động với vận tốc \(v\) có khối lượng \(m\) được tính bằng công thức:

   \[ K = \frac{1}{2} m v^2 \]

   Trong đó:

   • \(K\): Động năng (Joule)
   • \(m\): Khối lượng (kg)
   • \(v\): Vận tốc (m/s)
4. Công thức định luật 2 Newton:

   Liên hệ giữa gia tốc, lực và khối lượng của một vật được mô tả qua định luật 2 của Newton, công thức như sau:

   \[ F = m \cdot a \]

   Trong đó:

   • \(F\): Lực tác dụng (Newton)
   • \(m\): Khối lượng của vật (kg)
   • \(a\): Gia tốc (m/s²)
5. Công thức mô-men quán tính:

   Mô-men quán tính \((I)\) của một vật phụ thuộc vào khối lượng và vị trí phân bố của khối lượng đó quanh một trục quay:

   \[ I = \sum m_i r_i^2 \]

   Trong đó:

   • \(I\): Mô-men quán tính (kg.m²)
   • \(m_i\): Khối lượng của các phần tử (kg)
   • \(r_i\): Khoảng cách từ trục quay đến phần tử (m)

Các công thức trên là cơ sở giúp mở rộng hiểu biết về vận tốc và các đại lượng liên quan trong vật lý. Hiểu rõ các công thức này giúp bạn giải quyết tốt hơn các bài toán trong thực tế.

Việc chuyển đổi đơn vị vận tốc là một thao tác cần thiết khi bạn phải làm việc với các hệ thống đo lường khác nhau. Các đơn vị vận tốc phổ biến thường được sử dụng bao gồm: mét trên giây (m/s), kilômét trên giờ (km/h), dặm trên giờ (mph), và hải lý trên giờ (knot). Dưới đây là các phương pháp chuyển đổi đơn vị cơ bản.

1. Chuyển đổi từ m/s sang km/h:

   Để chuyển từ đơn vị mét trên giây (m/s) sang kilômét trên giờ (km/h), bạn nhân với 3.6:

   \[ v_{km/h} = v_{m/s} \times 3.6 \]
2. Chuyển đổi từ km/h sang m/s:

   Để chuyển từ đơn vị kilômét trên giờ (km/h) sang mét trên giây (m/s), bạn chia cho 3.6:

   \[ v_{m/s} = \frac{v_{km/h}}{3.6} \]
3. Chuyển đổi từ mph sang km/h:

   Để chuyển từ đơn vị dặm trên giờ (mph) sang kilômét trên giờ (km/h), bạn nhân với 1.609:

   \[ v_{km/h} = v_{mph} \times 1.609 \]
4. Chuyển đổi từ km/h sang mph:

   Để chuyển từ đơn vị kilômét trên giờ (km/h) sang dặm trên giờ (mph), bạn chia cho 1.609:

   \[ v_{mph} = \frac{v_{km/h}}{1.609} \]
5. Chuyển đổi từ knot sang km/h:

   Để chuyển từ đơn vị hải lý trên giờ (knot) sang kilômét trên giờ (km/h), bạn nhân với 1.852:

   \[ v_{km/h} = v_{knot} \times 1.852 \]
6. Chuyển đổi từ km/h sang knot:

   Để chuyển từ đơn vị kilômét trên giờ (km/h) sang hải lý trên giờ (knot), bạn chia cho 1.852:

   \[ v_{knot} = \frac{v_{km/h}}{1.852} \]

Những công thức chuyển đổi trên rất hữu ích khi bạn cần tính toán vận tốc và phải chuyển đổi giữa các hệ thống đo lường khác nhau, giúp bạn làm việc hiệu quả hơn trong nhiều lĩnh vực.

Để nắm vững cách tính vận tốc, việc thực hành qua các bài tập thực tiễn là vô cùng cần thiết. Dưới đây là một số bài tập vận dụng công thức tính vận tốc để giúp bạn hiểu rõ hơn.

1. Bài tập 1:

   Một ô tô di chuyển từ điểm A đến điểm B cách nhau 120 km trong 2 giờ. Tính vận tốc trung bình của ô tô.

   Giải:

   Sử dụng công thức tính vận tốc:

   \[ v = \frac{s}{t} \]

   Trong đó:

   • \(v\) là vận tốc (km/h)
   • \(s = 120\) km là quãng đường
   • \(t = 2\) giờ là thời gian

   Thay số vào công thức:

   \[ v = \frac{120}{2} = 60 \text{ km/h} \]

   Vậy vận tốc trung bình của ô tô là 60 km/h.

2. Bài tập 2:

   Một người đi bộ với vận tốc 5 km/h trong 3 giờ. Tính quãng đường mà người đó đã đi.

   Giải:

   Sử dụng công thức tính quãng đường:

   \[ s = v \times t \]

   Trong đó:

   • \(s\) là quãng đường (km)
   • \(v = 5\) km/h là vận tốc
   • \(t = 3\) giờ là thời gian

   Thay số vào công thức:

   \[ s = 5 \times 3 = 15 \text{ km} \]

   Vậy quãng đường người đó đã đi được là 15 km.

3. Bài tập 3:

   Một chiếc thuyền di chuyển với vận tốc 20 km/h. Sau 4 giờ, thuyền đã di chuyển được bao xa?

   Giải:

   Sử dụng công thức:

   \[ s = v \times t \]

   Với:

   • \(v = 20\) km/h
   • \(t = 4\) giờ

   Thay số vào công thức:

   \[ s = 20 \times 4 = 80 \text{ km} \]

   Vậy quãng đường thuyền đã di chuyển được là 80 km.

Những bài tập này giúp bạn luyện tập cách áp dụng công thức tính vận tốc trong nhiều tình huống thực tiễn khác nhau.

Qua bài viết này, chúng ta đã có cái nhìn toàn diện về khái niệm, công thức và ứng dụng của vận tốc trong đời sống cũng như trong các lĩnh vực khoa học kỹ thuật. Vận tốc không chỉ đơn thuần là một đại lượng vật lý biểu thị mức độ thay đổi vị trí theo thời gian, mà còn là một yếu tố quan trọng giúp chúng ta hiểu rõ hơn về các hiện tượng xung quanh.

Trong quá trình học tập và nghiên cứu, việc nắm vững kiến thức về vận tốc sẽ giúp bạn giải quyết hiệu quả các bài toán liên quan đến chuyển động. Bên cạnh đó, vận tốc còn là nền tảng để hiểu sâu hơn về các khái niệm phức tạp khác trong vật lý như động lượng, năng lượng, và động lực học.

Thực tế, vận tốc có ứng dụng rộng rãi trong nhiều lĩnh vực. Từ việc dự đoán thời gian di chuyển trong đời sống hàng ngày, tính toán và thiết kế trong kỹ thuật xây dựng, cho đến việc phân tích dòng chảy trong quản lý tài nguyên nước, vận tốc đều đóng vai trò quan trọng. Điều này khẳng định tầm quan trọng của việc học tập và áp dụng đúng các công thức tính vận tốc trong thực tiễn.

Như vậy, vận tốc không chỉ là một khái niệm học thuật mà còn là một công cụ hữu ích giúp chúng ta tối ưu hóa các hoạt động trong đời sống và công việc. Hy vọng rằng qua bài viết này, bạn đã củng cố được kiến thức cơ bản và nhận thức rõ hơn về tầm quan trọng của vận tốc trong cả lý thuyết và ứng dụng thực tế.