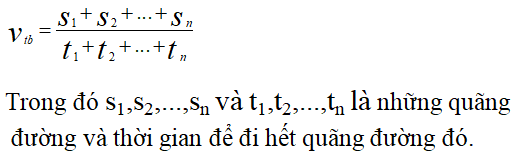Chủ đề cách tính vận tốc trung bình: Cách tính vận tốc trung bình là một khái niệm quan trọng trong vật lý học, giúp xác định tốc độ di chuyển của một vật thể trong một khoảng thời gian cụ thể. Bài viết này sẽ cung cấp hướng dẫn chi tiết và dễ hiểu nhất về cách tính vận tốc trung bình, kèm theo các ví dụ thực tế để bạn dễ dàng áp dụng.
Mục lục
Cách Tính Vận Tốc Trung Bình
Vận tốc trung bình là một đại lượng vật lý được sử dụng để xác định tốc độ di chuyển trung bình của một vật thể trong một khoảng thời gian nhất định. Để tính vận tốc trung bình, chúng ta sử dụng công thức:
\[
v_{tb} = \frac{s}{t}
\]
Trong đó:
- \(v_{tb}\): Vận tốc trung bình (m/s hoặc km/h)
- \(s\): Quãng đường đã đi được (m hoặc km)
- \(t\): Thời gian đã di chuyển (s hoặc h)
Ví Dụ Tính Vận Tốc Trung Bình
Ví dụ, một xe máy đi từ điểm A đến điểm B cách nhau 120 km trong 2 giờ. Vận tốc trung bình của xe máy này là:
\[
v_{tb} = \frac{120 \text{ km}}{2 \text{ h}} = 60 \text{ km/h}
\]
Công Thức Vận Tốc Trung Bình Trong Trường Hợp Đa Đoạn Đường
Nếu một vật di chuyển trên nhiều đoạn đường khác nhau với các vận tốc khác nhau, công thức vận tốc trung bình sẽ là:
\[
v_{tb} = \frac{s_1 + s_2 + ... + s_n}{t_1 + t_2 + ... + t_n}
\]
Trong đó:
- \(s_1, s_2, ..., s_n\): Các quãng đường trên các đoạn khác nhau.
- \(t_1, t_2, ..., t_n\): Thời gian di chuyển tương ứng trên từng đoạn.
Ứng Dụng Thực Tế Của Vận Tốc Trung Bình
Vận tốc trung bình được sử dụng rộng rãi trong đời sống hàng ngày, từ việc tính toán thời gian đi lại cho đến việc thiết kế các hệ thống giao thông và theo dõi hiệu suất hoạt động của các phương tiện giao thông.

.png)
1. Khái Niệm Về Vận Tốc Trung Bình
Vận tốc trung bình là một đại lượng vật lý được sử dụng để đo lường mức độ di chuyển của một vật thể trong một khoảng thời gian cụ thể. Nó được định nghĩa là tỉ số giữa quãng đường mà vật thể đã di chuyển và khoảng thời gian mà vật thể di chuyển.
Công thức cơ bản để tính vận tốc trung bình là:
\[
v_{tb} = \frac{s}{t}
\]
- \(v_{tb}\): Vận tốc trung bình (m/s hoặc km/h)
- \(s\): Quãng đường đã đi được (m hoặc km)
- \(t\): Thời gian đã di chuyển (s hoặc h)
Vận tốc trung bình cho chúng ta biết trung bình, một vật thể di chuyển bao nhiêu quãng đường trong một đơn vị thời gian nhất định. Đây là một khái niệm quan trọng, không chỉ trong lĩnh vực vật lý mà còn trong cuộc sống hàng ngày, như khi chúng ta tính toán thời gian và tốc độ di chuyển của các phương tiện giao thông.
Vận tốc trung bình khác với vận tốc tức thời ở chỗ nó không tính đến sự thay đổi của vận tốc trong suốt quá trình di chuyển, mà chỉ quan tâm đến kết quả cuối cùng sau một khoảng thời gian cụ thể.
2. Phương Pháp Tính Vận Tốc Trung Bình
Vận tốc trung bình có thể được tính toán thông qua nhiều phương pháp khác nhau, tùy thuộc vào đặc tính của chuyển động và điều kiện cụ thể. Dưới đây là các phương pháp phổ biến để tính vận tốc trung bình:
- Phương pháp 1: Tính vận tốc trung bình trên quãng đường thẳng
- \(v_{tb}\): Vận tốc trung bình
- \(s\): Quãng đường thẳng đã đi được
- \(t\): Thời gian di chuyển
- Phương pháp 2: Tính vận tốc trung bình trong chuyển động không đều
- Phương pháp 3: Tính vận tốc trung bình trong chuyển động tròn
- \(C\): Chu vi của đường tròn
- \(t\): Thời gian để hoàn thành một vòng tròn
Đây là phương pháp cơ bản và phổ biến nhất, thường áp dụng khi vật thể di chuyển trên một quãng đường thẳng mà không có sự thay đổi đáng kể về hướng đi.
Công thức áp dụng là:
\[
v_{tb} = \frac{s}{t}
\]
Khi vật thể di chuyển với vận tốc thay đổi liên tục, việc tính vận tốc trung bình đòi hỏi phải chia quãng đường thành nhiều đoạn nhỏ, mỗi đoạn có vận tốc khác nhau. Sau đó, vận tốc trung bình được tính bằng cách lấy tổng quãng đường chia cho tổng thời gian.
Công thức áp dụng là:
\[
v_{tb} = \frac{s_1 + s_2 + ... + s_n}{t_1 + t_2 + ... + t_n}
\]
Trong trường hợp chuyển động tròn, vận tốc trung bình được tính dựa trên chu vi của đường tròn mà vật thể đã đi qua và thời gian hoàn thành một vòng tròn.
Công thức áp dụng là:
\[
v_{tb} = \frac{C}{t}
\]
Mỗi phương pháp đều có ứng dụng cụ thể, giúp người học và người thực hành xác định vận tốc trung bình của vật thể trong các điều kiện khác nhau.

3. Ví Dụ Minh Họa Cách Tính Vận Tốc Trung Bình
Dưới đây là một số ví dụ minh họa cách tính vận tốc trung bình, giúp bạn hiểu rõ hơn về cách áp dụng các công thức đã học.
Ví dụ 1: Tính vận tốc trung bình trên quãng đường thẳng
Một chiếc xe di chuyển trên quãng đường 120 km trong thời gian 2 giờ. Hãy tính vận tốc trung bình của chiếc xe.
Giải:
- Quãng đường \( s = 120 \, km \)
- Thời gian \( t = 2 \, giờ \)
Áp dụng công thức tính vận tốc trung bình:
\[
v_{tb} = \frac{s}{t} = \frac{120 \, km}{2 \, giờ} = 60 \, km/h
\]
Vậy, vận tốc trung bình của chiếc xe là 60 km/h.
Ví dụ 2: Tính vận tốc trung bình trong chuyển động không đều
Một người chạy bộ trên quãng đường tổng cộng 10 km, với 5 km đầu tiên chạy trong 30 phút và 5 km tiếp theo chạy trong 45 phút. Tính vận tốc trung bình của người đó.
Giải:
- Quãng đường \( s_1 = 5 \, km \), \( s_2 = 5 \, km \)
- Thời gian \( t_1 = 0.5 \, giờ \), \( t_2 = 0.75 \, giờ \)
Vận tốc trung bình của người chạy được tính như sau:
\[
v_{tb} = \frac{s_1 + s_2}{t_1 + t_2} = \frac{5 \, km + 5 \, km}{0.5 \, giờ + 0.75 \, giờ} = \frac{10 \, km}{1.25 \, giờ} = 8 \, km/h
\]
Vậy, vận tốc trung bình của người chạy là 8 km/h.
Ví dụ 3: Tính vận tốc trung bình trong chuyển động tròn
Một chiếc xe đua chạy quanh một đường tròn có chu vi 400 m và hoàn thành một vòng trong 20 giây. Tính vận tốc trung bình của chiếc xe.
Giải:
- Chu vi đường tròn \( C = 400 \, m \)
- Thời gian \( t = 20 \, giây \)
Vận tốc trung bình của chiếc xe đua được tính như sau:
\[
v_{tb} = \frac{C}{t} = \frac{400 \, m}{20 \, giây} = 20 \, m/s
\]
Vậy, vận tốc trung bình của chiếc xe đua là 20 m/s.

4. Ứng Dụng Của Vận Tốc Trung Bình
Vận tốc trung bình không chỉ là một khái niệm cơ bản trong vật lý mà còn có nhiều ứng dụng thực tiễn trong đời sống và khoa học. Dưới đây là một số ứng dụng tiêu biểu:
1. Giao thông vận tải
Trong giao thông, vận tốc trung bình giúp xác định thời gian cần thiết để di chuyển giữa các địa điểm. Điều này hỗ trợ trong việc lên kế hoạch hành trình và tối ưu hóa lộ trình di chuyển.
2. Thể thao
Trong các môn thể thao như chạy bộ, đua xe, hay bơi lội, vận tốc trung bình được sử dụng để đánh giá hiệu suất của vận động viên và lập kế hoạch huấn luyện.
3. Nghiên cứu khoa học
Trong nghiên cứu khoa học, vận tốc trung bình giúp các nhà nghiên cứu phân tích các hiện tượng chuyển động và đưa ra các kết luận về đặc tính của đối tượng nghiên cứu.
4. Quản lý năng lượng
Vận tốc trung bình có thể được sử dụng để tính toán mức tiêu thụ năng lượng của các phương tiện và thiết bị, giúp tối ưu hóa hiệu suất và giảm thiểu tiêu hao năng lượng.
5. Hàng không và vũ trụ
Trong ngành hàng không và vũ trụ, vận tốc trung bình là yếu tố quan trọng trong việc tính toán lộ trình bay, thời gian bay, và tiêu thụ nhiên liệu, từ đó đảm bảo an toàn và hiệu quả trong các chuyến bay.

5. Một Số Lưu Ý Khi Tính Vận Tốc Trung Bình
Khi tính vận tốc trung bình, có một số điểm quan trọng cần lưu ý để đảm bảo tính chính xác và áp dụng đúng công thức:
- Chọn đơn vị phù hợp: Đảm bảo rằng các đại lượng thời gian và khoảng cách sử dụng cùng một đơn vị trước khi thực hiện phép tính. Nếu không, cần đổi đơn vị để tránh sai số.
- Phân biệt giữa vận tốc trung bình và vận tốc tức thời: Vận tốc trung bình là tổng quãng đường chia cho tổng thời gian, trong khi vận tốc tức thời là vận tốc tại một thời điểm cụ thể. Hai khái niệm này không thể hoán đổi cho nhau.
- Tính tổng quãng đường và thời gian: Khi vật thể di chuyển qua nhiều đoạn đường với các vận tốc khác nhau, cần tính tổng tất cả các quãng đường đã đi và tổng thời gian để có thể tính được vận tốc trung bình chính xác.
- Không bỏ qua các yếu tố khác: Trong thực tế, có thể cần xem xét các yếu tố khác như địa hình, điều kiện thời tiết, và sức cản để có được một kết quả phù hợp nhất.
- Áp dụng đúng công thức: Công thức vận tốc trung bình đơn giản nhất là: \[ v_{tb} = \frac{\Delta s}{\Delta t} \] Trong đó, \(\Delta s\) là tổng quãng đường đi được, và \(\Delta t\) là tổng thời gian di chuyển.