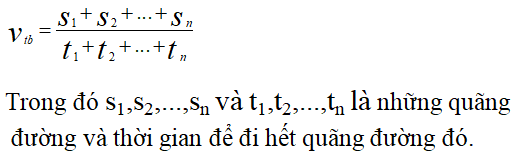Chủ đề tính vận tốc trung bình lý 10: Trong bài viết này, chúng ta sẽ khám phá chi tiết cách tính vận tốc trung bình trong chương trình Vật Lý lớp 10. Từ những công thức cơ bản đến các ví dụ thực tế, bài viết giúp bạn hiểu rõ hơn và áp dụng kiến thức vào thực tế một cách hiệu quả và chính xác.
Mục lục
- Tính Vận Tốc Trung Bình Lý 10
- 1. Định nghĩa và công thức tính vận tốc trung bình
- 2. Sự khác biệt giữa vận tốc và tốc độ
- 3. Các dạng bài tập tính vận tốc trung bình
- 4. Ứng dụng của vận tốc trung bình trong thực tế
- 5. Câu hỏi trắc nghiệm về vận tốc trung bình
- 6. Luyện tập và kiểm tra kiến thức
- 7. Tài liệu tham khảo và học tập thêm
Tính Vận Tốc Trung Bình Lý 10
Trong chương trình Vật lý lớp 10, khái niệm vận tốc trung bình là một phần quan trọng trong việc nghiên cứu chuyển động của các vật thể. Vận tốc trung bình cho phép học sinh hiểu rõ hơn về chuyển động của vật thể trong một khoảng thời gian nhất định. Dưới đây là các thông tin chi tiết và các ứng dụng cụ thể của công thức tính vận tốc trung bình.
1. Khái niệm Vận Tốc Trung Bình
Vận tốc trung bình là tổng quãng đường đi được chia cho tổng thời gian để đi quãng đường đó. Công thức tính vận tốc trung bình được viết như sau:
\[ V_{tb} = \frac{S}{t} \]
- \( V_{tb} \): Vận tốc trung bình
- \( S \): Tổng quãng đường di chuyển
- \( t \): Tổng thời gian di chuyển
2. Ứng Dụng Công Thức Tính Vận Tốc Trung Bình
- Trong giao thông: Công thức này giúp tính toán thời gian di chuyển trung bình giữa các điểm trên mạng lưới đường bộ, từ đó cải thiện lưu thông và giảm tắc nghẽn.
- Trong thể thao: Vận tốc trung bình giúp xác định hiệu suất và chiến lược của vận động viên trong các môn đua xe, đua thuyền.
- Trong khoa học môi trường: Được sử dụng để nghiên cứu dòng chảy của nước trong sông, suối và phân tích sự phân bố các chất ô nhiễm.
3. Ví Dụ Minh Họa
Ví dụ: Một chiếc xe di chuyển từ thành phố A đến thành phố B với vận tốc 60 km/h trong 2 giờ, sau đó quay lại A với vận tốc 40 km/h trong 3 giờ.
- Bước 1: Tính tổng quãng đường di chuyển.
- Quãng đường đi: \(60 \, \text{km/h} \times 2 \, \text{h} = 120 \, \text{km}\)
- Quãng đường về: \(40 \, \text{km/h} \times 3 \, \text{h} = 120 \, \text{km}\)
- Tổng quãng đường: \(120 \, \text{km} + 120 \, \text{km} = 240 \, \text{km}\)
- Bước 2: Tính tổng thời gian di chuyển.
- Tổng thời gian: \(2 \, \text{h} + 3 \, \text{h} = 5 \, \text{h}\)
- Bước 3: Áp dụng công thức vận tốc trung bình.
- \[ V_{tb} = \frac{S}{t} = \frac{240 \, \text{km}}{5 \, \text{h}} = 48 \, \text{km/h} \]
4. Bài Tập Thực Hành
| Bài Tập | Lời Giải |
|---|---|
| Một người đi bộ 4 km trong 50 phút. Tính vận tốc trung bình của người đó. |
|
| Một tàu hỏa chạy từ ga A đến ga B với vận tốc 80 km/h trong 2 giờ đầu và 60 km/h trong 1 giờ tiếp theo. Tính vận tốc trung bình của tàu. |
|

.png)
1. Định nghĩa và công thức tính vận tốc trung bình
Vận tốc trung bình là đại lượng vật lý dùng để mô tả quãng đường mà một vật di chuyển được trong một khoảng thời gian nhất định. Nó được tính bằng cách lấy tổng quãng đường di chuyển chia cho tổng thời gian di chuyển.
Công thức tổng quát để tính vận tốc trung bình được biểu diễn như sau:
Trong đó:
- \(V_{tb}\): Vận tốc trung bình (đơn vị: km/h hoặc m/s).
- \(S\): Tổng quãng đường di chuyển (đơn vị: km hoặc m).
- \(t\): Tổng thời gian di chuyển (đơn vị: h hoặc s).
Để áp dụng công thức này vào bài toán cụ thể, chúng ta cần xác định rõ quãng đường và thời gian di chuyển. Dưới đây là một ví dụ minh họa cách tính vận tốc trung bình:
- Ví dụ: Một chiếc xe chạy từ điểm A đến điểm B với vận tốc 60 km/h trong 2 giờ, sau đó quay trở lại điểm A với vận tốc 40 km/h trong 3 giờ.
- Bước 1: Tính tổng quãng đường di chuyển.
- Quãng đường đi: \(60 \times 2 = 120\) km
- Quãng đường về: \(40 \times 3 = 120\) km
- Tổng quãng đường: \(120 + 120 = 240\) km
- Bước 2: Tính tổng thời gian di chuyển.
- Tổng thời gian: \(2 + 3 = 5\) giờ
- Bước 3: Áp dụng công thức vận tốc trung bình. \[ V_{tb} = \frac{S}{t} = \frac{240}{5} = 48 \text{ km/h} \]
Như vậy, vận tốc trung bình của chiếc xe trong suốt hành trình là 48 km/h. Công thức tính vận tốc trung bình không chỉ được sử dụng trong các bài toán vật lý mà còn có nhiều ứng dụng trong thực tế như phân tích giao thông, thể thao, và khoa học môi trường.
2. Sự khác biệt giữa vận tốc và tốc độ
Trong vật lý, "vận tốc" và "tốc độ" thường được sử dụng để mô tả chuyển động, nhưng chúng có sự khác biệt cơ bản về mặt định nghĩa và tính chất:
- Vận tốc: Là đại lượng vector, có nghĩa là nó không chỉ có độ lớn mà còn có hướng. Vận tốc biểu thị sự thay đổi vị trí của vật theo thời gian, và được tính bằng công thức: \[ \vec{v} = \frac{\Delta \vec{s}}{\Delta t} \] trong đó \(\Delta \vec{s}\) là độ dời (một vector) và \(\Delta t\) là khoảng thời gian.
- Tốc độ: Là đại lượng vô hướng, chỉ có độ lớn mà không có hướng. Tốc độ được định nghĩa là khoảng cách đi được trên đơn vị thời gian và được tính bằng công thức: \[ v = \frac{s}{t} \] trong đó \(s\) là quãng đường đi được (một đại lượng vô hướng) và \(t\) là thời gian.
Chính sự khác biệt giữa đại lượng vector (vận tốc) và vô hướng (tốc độ) này làm cho hai khái niệm không thể sử dụng thay thế lẫn nhau. Trong khi vận tốc cần chú ý đến cả hướng di chuyển của vật, tốc độ chỉ quan tâm đến độ lớn của chuyển động, bất kể hướng nào.
Do đó, khi học và làm bài tập, học sinh cần phân biệt rõ ràng giữa hai khái niệm này để áp dụng đúng công thức và hiểu đúng bản chất của các bài toán vật lý liên quan đến chuyển động.

3. Các dạng bài tập tính vận tốc trung bình
Để hiểu rõ hơn về cách tính vận tốc trung bình, chúng ta hãy xem xét một số dạng bài tập phổ biến và các bước giải chi tiết:
-
Bài tập 1: Tính vận tốc trung bình trong chuyển động một chiều
Một xe đạp di chuyển từ điểm A đến điểm B với quãng đường \( S = 15 \) km trong thời gian \( t = 0.75 \) giờ. Tính vận tốc trung bình.
- Bước 1: Sử dụng công thức \( V_{tb} = \frac{S}{t} \)
- Bước 2: Thay số vào công thức: \( V_{tb} = \frac{15}{0.75} = 20 \) km/h
- Kết luận: Vận tốc trung bình của xe đạp là 20 km/h.
-
Bài tập 2: Tính vận tốc trung bình trong chuyến đi khứ hồi
Một ô tô đi từ thành phố X đến thành phố Y với vận tốc \(v_1 = 60\) km/h trong thời gian \(t_1 = 2\) giờ và quay trở lại X với vận tốc \(v_2 = 40\) km/h trong thời gian \(t_2 = 3\) giờ. Tính vận tốc trung bình cho cả chuyến đi và về.
- Bước 1: Tính tổng quãng đường \( S = v_1 \cdot t_1 + v_2 \cdot t_2 \)
- Bước 2: Thay số vào công thức: \( S = 60 \times 2 + 40 \times 3 = 240 \) km
- Bước 3: Tính tổng thời gian \( T = t_1 + t_2 = 2 + 3 = 5 \) giờ
- Bước 4: Tính vận tốc trung bình \( V_{tb} = \frac{S}{T} = \frac{240}{5} = 48 \) km/h
- Kết luận: Vận tốc trung bình cho cả chuyến đi và về là 48 km/h.
-
Bài tập 3: Tính vận tốc trung bình với các khoảng thời gian khác nhau
Một tàu hỏa chạy từ ga A đến ga B với vận tốc 80 km/h trong 2 giờ đầu và 60 km/h trong 1 giờ tiếp theo. Tính vận tốc trung bình của tàu trên cả chuyến đi.
- Bước 1: Tính quãng đường tàu đi trong 2 giờ đầu \( S_1 = 80 \times 2 = 160 \) km
- Bước 2: Tính quãng đường tàu đi trong 1 giờ sau \( S_2 = 60 \times 1 = 60 \) km
- Bước 3: Tính tổng quãng đường \( S = S_1 + S_2 = 160 + 60 = 220 \) km
- Bước 4: Tính tổng thời gian \( t = 2 + 1 = 3 \) giờ
- Bước 5: Tính vận tốc trung bình \( V_{tb} = \frac{S}{t} = \frac{220}{3} \approx 73.33 \) km/h
- Kết luận: Vận tốc trung bình của tàu trên cả chuyến đi là khoảng 73.33 km/h.
Các dạng bài tập trên minh họa rõ ràng cách sử dụng công thức tính vận tốc trung bình trong các tình huống khác nhau. Hãy luyện tập thêm với nhiều dạng bài tập khác để nắm vững khái niệm này.

4. Ứng dụng của vận tốc trung bình trong thực tế
Vận tốc trung bình không chỉ là một khái niệm quan trọng trong lý thuyết vật lý, mà còn có nhiều ứng dụng thực tế trong cuộc sống hàng ngày và các ngành khoa học khác. Dưới đây là một số ví dụ cụ thể về cách vận tốc trung bình được áp dụng trong thực tế:
- Phân tích giao thông: Vận tốc trung bình được sử dụng để tính toán thời gian di chuyển trung bình giữa các điểm khác nhau trên mạng lưới đường bộ. Điều này giúp các nhà quy hoạch đô thị và kỹ sư giao thông cải thiện lưu thông, giảm tắc nghẽn và tối ưu hóa lộ trình.
- Thể thao: Trong các môn thể thao như đua xe hay đua thuyền, vận tốc trung bình giúp xác định hiệu suất của vận động viên và đánh giá chiến lược trong suốt cuộc đua. Việc phân tích vận tốc trung bình có thể cung cấp thông tin quan trọng về cách quản lý năng lượng và tăng tốc độ đúng lúc.
- Vận tải và logistics: Các công ty vận tải sử dụng vận tốc trung bình để ước tính thời gian giao hàng và lên kế hoạch lộ trình hiệu quả. Điều này giúp tối ưu hóa chi phí vận chuyển và đảm bảo thời gian giao hàng chính xác.
- Khoa học môi trường: Các nhà khoa học sử dụng vận tốc trung bình của dòng nước trong sông suối để nghiên cứu sự phân bố của các chất ô nhiễm, đánh giá tác động đến môi trường và lập kế hoạch bảo vệ tài nguyên nước.
Như vậy, vận tốc trung bình không chỉ giúp chúng ta hiểu rõ hơn về các chuyển động và tốc độ, mà còn có vai trò quan trọng trong nhiều lĩnh vực khác nhau. Điều này làm nổi bật tính ứng dụng cao và sự cần thiết của việc nắm vững kiến thức về vận tốc trung bình trong cả học tập và thực tế.

5. Câu hỏi trắc nghiệm về vận tốc trung bình
Các câu hỏi trắc nghiệm dưới đây giúp bạn ôn tập và củng cố kiến thức về vận tốc trung bình trong vật lý lớp 10. Các câu hỏi được thiết kế để kiểm tra hiểu biết về công thức tính vận tốc trung bình, các khái niệm liên quan, và ứng dụng của vận tốc trung bình trong các bài toán thực tế.
-
Câu 1: Một người đi xe đạp di chuyển từ điểm A đến điểm B với quãng đường \(s = 12 \, km\). Trong nửa thời gian đầu, người này đi với vận tốc \(v_1 = 10 \, km/h\) và trong nửa thời gian sau đi với vận tốc \(v_2 = 15 \, km/h\). Hỏi vận tốc trung bình của người đó trên cả quãng đường AB là bao nhiêu?
- \(12 \, km/h\)
- \(13 \, km/h\)
- \(14 \, km/h\)
- \(15 \, km/h\)
-
Câu 2: Một ô tô đi trên đoạn đường thẳng từ thành phố X đến thành phố Y. Trong nửa quãng đường đầu, ô tô đi với vận tốc \(v_1 = 60 \, km/h\) và trong nửa quãng đường sau đi với vận tốc \(v_2 = 40 \, km/h\). Tính vận tốc trung bình của ô tô trên cả quãng đường.
- \(45 \, km/h\)
- \(48 \, km/h\)
- \(50 \, km/h\)
- \(55 \, km/h\)
-
Câu 3: Một tàu thủy đi từ bến A đến bến B trong 3 giờ với vận tốc \(v_1 = 20 \, km/h\) và từ bến B đến bến C trong 2 giờ với vận tốc \(v_2 = 30 \, km/h\). Hỏi vận tốc trung bình của tàu thủy trên cả hành trình là bao nhiêu?
- \(22 \, km/h\)
- \(24 \, km/h\)
- \(26 \, km/h\)
- \(28 \, km/h\)
-
Câu 4: Một vận động viên chạy trên một quãng đường thẳng với tốc độ thay đổi. Trong \(1/3\) quãng đường đầu, vận động viên chạy với vận tốc \(v_1 = 10 \, m/s\), \(1/3\) quãng đường tiếp theo với vận tốc \(v_2 = 12 \, m/s\), và \(1/3\) quãng đường cuối cùng với vận tốc \(v_3 = 8 \, m/s\). Tính vận tốc trung bình của vận động viên trên cả quãng đường.
- \(9.33 \, m/s\)
- \(10 \, m/s\)
- \(10.67 \, m/s\)
- \(11 \, m/s\)
Trả lời các câu hỏi trên giúp bạn nắm vững hơn cách tính và ứng dụng của vận tốc trung bình trong các tình huống khác nhau. Để tính vận tốc trung bình (\(v_{tb}\)), bạn cần nhớ công thức:
\[
v_{tb} = \frac{s}{\Delta t}
\]
trong đó \(s\) là tổng quãng đường đi được và \(\Delta t\) là tổng thời gian di chuyển.
XEM THÊM:
6. Luyện tập và kiểm tra kiến thức
6.1. Đề thi thử và đáp án
Để củng cố kiến thức và kỹ năng giải bài tập, học sinh có thể tham khảo các đề thi thử dưới đây:
-
Đề thi thử 1: Tính vận tốc trung bình của một vật di chuyển theo quãng đường \(s\) trong thời gian \(t\).
Bài toán: Một chiếc xe máy di chuyển trên một đoạn đường 100 km trong thời gian 2 giờ. Tính vận tốc trung bình của xe.
Đáp án: Vận tốc trung bình \(v_{tb}\) được tính bằng công thức:
\[
v_{tb} = \frac{s}{t} = \frac{100 \text{ km}}{2 \text{ giờ}} = 50 \text{ km/h}
\] -
Đề thi thử 2: Tính vận tốc trung bình trong trường hợp vận tốc thay đổi.
Bài toán: Một chiếc xe ô tô đi từ A đến B với vận tốc 40 km/h và quay trở lại từ B đến A với vận tốc 60 km/h. Tính vận tốc trung bình của xe trên cả quãng đường.
Đáp án: Giả sử quãng đường từ A đến B là \(s\), vận tốc trung bình \(v_{tb}\) trên cả quãng đường là:
\[
v_{tb} = \frac{2s}{\frac{s}{v_1} + \frac{s}{v_2}} = \frac{2 \times 60 \times 40}{60 + 40} = 48 \text{ km/h}
\]
6.2. Các bài tập tự luyện
Dưới đây là các bài tập tự luyện giúp học sinh rèn luyện kỹ năng giải bài tập về vận tốc trung bình:
- Bài tập 1: Một người đi bộ quãng đường 300 m trong 5 phút. Tính vận tốc trung bình của người đó.
- Bài tập 2: Một chiếc xe chạy 150 km với vận tốc 50 km/h và sau đó chạy thêm 200 km với vận tốc 80 km/h. Hãy tính vận tốc trung bình của xe trên toàn bộ quãng đường.
- Bài tập 3: Một tàu hỏa di chuyển với vận tốc 70 km/h trên quãng đường 140 km và sau đó tiếp tục di chuyển với vận tốc 90 km/h trên quãng đường 180 km. Tính vận tốc trung bình của tàu hỏa.
Học sinh nên giải các bài tập trên và so sánh kết quả với bạn bè hoặc giáo viên để hiểu rõ hơn về cách tính vận tốc trung bình.

7. Tài liệu tham khảo và học tập thêm
Để nắm vững hơn về cách tính vận tốc trung bình, các bạn học sinh lớp 10 có thể tham khảo các nguồn tài liệu dưới đây, bao gồm các bài giảng, bài tập và ví dụ minh họa chi tiết:
- Hệ thống bài tập về vận tốc trung bình: Học sinh có thể luyện tập với các bài tập dạng vận tốc trung bình để củng cố kiến thức. Các bài tập này bao gồm nhiều trường hợp khác nhau, như tính vận tốc trung bình trên nhiều đoạn đường với các vận tốc khác nhau hoặc vận tốc trung bình trên toàn bộ hành trình. Các bài tập thực tế sẽ giúp bạn hiểu rõ hơn về ứng dụng của công thức \( v_{tb} = \frac{s}{t} \).
- Bài giảng video trực tuyến: Các video giảng dạy về chủ đề này cung cấp hướng dẫn chi tiết về cách tính vận tốc trung bình, từ các ví dụ đơn giản đến các tình huống phức tạp hơn, giúp học sinh nắm bắt bài học một cách dễ dàng hơn.
- Tài liệu học thêm: Các tài liệu trực tuyến như PDF hoặc ebook chứa đựng nhiều dạng bài tập và hướng dẫn giải chi tiết, kèm theo lý thuyết căn bản. Đây là nguồn tài liệu quý giá giúp bạn tự học và chuẩn bị cho các kỳ thi.
- Diễn đàn học tập: Tham gia các diễn đàn trực tuyến là một cách tốt để học sinh trao đổi kiến thức, hỏi đáp và thảo luận về các bài tập liên quan đến vận tốc trung bình. Tại đây, bạn có thể nhận được sự hỗ trợ từ các giáo viên và bạn bè.
Học sinh cần kết hợp nhiều nguồn tài liệu để có cái nhìn toàn diện hơn về vận tốc trung bình, cũng như phát triển kỹ năng giải bài tập trong quá trình học tập môn Vật lý 10.