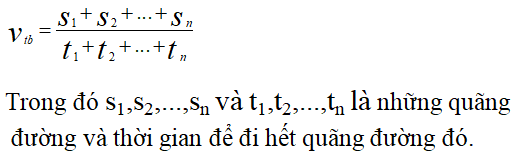Tính Vận Tốc Trung Bình Toán Lớp 5: Hướng Dẫn Chi Tiết và Bài Tập Thực Hành

Vận tốc trung bình là một khái niệm quan trọng trong toán học và vật lý, đặc biệt đối với học sinh lớp 5. Đây là kiến thức cơ bản giúp học sinh hiểu rõ hơn về các chuyển động và tính toán các bài toán về thời gian, quãng đường và vận tốc. Công thức tính vận tốc trung bình có thể áp dụng cho nhiều trường hợp khác nhau.

Công Thức Tính Vận Tốc Trung Bình

Công thức tổng quát để tính vận tốc trung bình:

\[ V_{tb} = \frac{S}{t} \]

Trong đó:

• \( V_{tb} \): Vận tốc trung bình
• \( S \): Quãng đường đi được
• \( t \): Thời gian di chuyển

Ví Dụ Về Tính Vận Tốc Trung Bình

Ví dụ, một người đi bộ với quãng đường 10 km trong thời gian 2 giờ. Vận tốc trung bình của người đó được tính như sau:

\[ V_{tb} = \frac{10}{2} = 5 \text{ km/h} \]

Các Bước Để Tính Vận Tốc Trung Bình

1. Xác định quãng đường \( S \) mà vật đã di chuyển.
2. Đo thời gian \( t \) mà vật đã di chuyển từ điểm bắt đầu đến điểm kết thúc.
3. Áp dụng công thức \( V_{tb} = \frac{S}{t} \) để tính vận tốc trung bình.

Bài Tập Mẫu

Một ô tô đi từ A đến B với vận tốc 50 km/h và tiếp tục từ B đến C với vận tốc 70 km/h. Quãng đường từ A đến B là 120 km và từ B đến C là 180 km. Tính vận tốc trung bình của ô tô trên cả hai quãng đường.

Lời giải:

Áp dụng công thức:

\[ V_{tb} = \frac{120 + 180}{\frac{120}{50} + \frac{180}{70}} \]

Ta có:

\[ V_{tb} = \frac{300}{\frac{120}{50} + \frac{180}{70}} = \frac{300}{2.4 + 2.57} = 59.34 \text{ km/h} \]

Kết Luận

Việc tính vận tốc trung bình giúp học sinh không chỉ hiểu rõ hơn về chuyển động mà còn rèn luyện khả năng áp dụng công thức vào các bài toán thực tế. Đây là kiến thức cần thiết để các em chuẩn bị tốt hơn cho các cấp học cao hơn.

Vận tốc trung bình là đại lượng biểu thị mức độ nhanh hay chậm của một vật khi di chuyển trong một khoảng thời gian xác định. Nó được tính bằng cách lấy quãng đường đã di chuyển chia cho thời gian đã di chuyển.

• Công thức tính vận tốc trung bình: \[ V_{\text{tb}} = \frac{S}{t} \]
• Trong đó:
  • \( V_{\text{tb}} \) là vận tốc trung bình (km/h hoặc m/s).
  • \( S \) là quãng đường đã di chuyển (km hoặc m).
  • \( t \) là thời gian đã di chuyển (giờ hoặc giây).

Việc hiểu rõ khái niệm và công thức tính vận tốc trung bình giúp học sinh lớp 5 có thể áp dụng vào các bài toán thực tế như tính vận tốc của một chiếc xe hay vận tốc của một người đi bộ.

Công thức tính vận tốc trung bình giúp học sinh xác định được vận tốc của một vật khi di chuyển trên quãng đường nhất định trong một khoảng thời gian cụ thể. Công thức này được biểu diễn như sau:

• Công thức tổng quát: \[ V_{\text{tb}} = \frac{S}{t} \]
• Trong đó:
  • \( V_{\text{tb}} \) là vận tốc trung bình (đơn vị km/h hoặc m/s).
  • \( S \) là quãng đường vật di chuyển (đơn vị km hoặc m).
  • \( t \) là thời gian vật di chuyển (đơn vị giờ hoặc giây).

Ví dụ: Nếu một chiếc xe chạy được quãng đường 60 km trong 2 giờ, vận tốc trung bình của xe sẽ được tính bằng:

• \[ V_{\text{tb}} = \frac{60}{2} = 30 \, \text{km/h} \]

Bài toán tính vận tốc trung bình rất hữu ích trong việc giải quyết các tình huống thực tế như tốc độ di chuyển của xe cộ, người đi bộ, hoặc tàu thuyền.

Các bài toán về vận tốc trung bình trong chương trình Toán lớp 5 thường được phân loại dựa trên quãng đường, thời gian, và vận tốc. Điều này giúp học sinh nắm rõ cách áp dụng công thức trong từng tình huống cụ thể. Dưới đây là các dạng bài toán chính:

• Dạng 1: Bài toán tính vận tốc trung bình dựa trên quãng đường và thời gian đã biết:
  • Công thức áp dụng: \[ V_{\text{tb}} = \frac{S}{t} \]
  • Ví dụ: Một xe máy đi được quãng đường 80 km trong 4 giờ. Vận tốc trung bình của xe là bao nhiêu?
• Dạng 2: Bài toán tính quãng đường khi biết vận tốc trung bình và thời gian:
  • Công thức áp dụng: \[ S = V_{\text{tb}} \times t \]
  • Ví dụ: Một chiếc xe chạy với vận tốc trung bình 50 km/h trong 3 giờ. Tính quãng đường xe đã đi được.
• Dạng 3: Bài toán tính thời gian khi biết vận tốc trung bình và quãng đường:
  • Công thức áp dụng: \[ t = \frac{S}{V_{\text{tb}}} \]
  • Ví dụ: Một người đi bộ với vận tốc trung bình 5 km/h và đã đi được quãng đường 15 km. Tính thời gian người đó đã đi.

Dưới đây là một số bài tập giúp học sinh luyện tập và vận dụng công thức tính vận tốc trung bình trong các tình huống thực tế. Các bài tập này được thiết kế để củng cố kiến thức về quãng đường, thời gian và vận tốc.

• Bài tập 1: Một chiếc xe đạp đi được quãng đường 40 km trong 2 giờ. Tính vận tốc trung bình của xe đạp.
  • Gợi ý: Áp dụng công thức \[ V_{\text{tb}} = \frac{S}{t} \]
  • Lời giải: \[ V_{\text{tb}} = \frac{40}{2} = 20 \, \text{km/h} \]
• Bài tập 2: Một người đi bộ trong 3 giờ với vận tốc trung bình 4 km/h. Tính quãng đường người đó đã đi được.
  • Gợi ý: Áp dụng công thức \[ S = V_{\text{tb}} \times t \]
  • Lời giải: \[ S = 4 \times 3 = 12 \, \text{km} \]
• Bài tập 3: Một ô tô đi được 150 km với vận tốc trung bình 50 km/h. Tính thời gian mà ô tô đã đi.
  • Gợi ý: Áp dụng công thức \[ t = \frac{S}{V_{\text{tb}}} \]
  • Lời giải: \[ t = \frac{150}{50} = 3 \, \text{giờ} \]
• Bài tập 4: Một chiếc thuyền đi được 60 km trong 4 giờ. Nếu vận tốc trung bình của thuyền tăng thêm 5 km/h, thì quãng đường thuyền đi trong cùng thời gian là bao nhiêu?
  • Gợi ý: Tính vận tốc mới và áp dụng công thức \[ S = V_{\text{tb}} \times t \]
  • Lời giải: Vận tốc mới \[ V_{\text{mới}} = 15 + 5 = 20 \, \text{km/h} \]
  • Quãng đường mới: \[ S = 20 \times 4 = 80 \, \text{km} \]

Để giải các bài toán liên quan đến vận tốc trung bình, học sinh cần nắm vững công thức tính vận tốc trung bình và cách áp dụng trong các tình huống khác nhau. Dưới đây là các bước cụ thể giúp học sinh tiếp cận bài toán một cách hiệu quả.

1. Xác định các đại lượng cần tìm:
   • Quãng đường (\(S\))
   • Thời gian (\(t\))
   • Vận tốc trung bình (\(V_{\text{tb}}\))
2. Viết công thức cần áp dụng:

   Áp dụng công thức tính vận tốc trung bình:

   \[ V_{\text{tb}} = \frac{S}{t} \]

   Nếu đã biết quãng đường và thời gian, tính vận tốc bằng cách chia quãng đường cho thời gian.

3. Thay giá trị vào công thức:
   • Nếu biết quãng đường và thời gian, thay các giá trị tương ứng vào công thức trên để tìm vận tốc.
   • Nếu biết vận tốc và thời gian, tính quãng đường bằng công thức: \[ S = V_{\text{tb}} \times t \]
   • Nếu biết quãng đường và vận tốc, tính thời gian bằng công thức: \[ t = \frac{S}{V_{\text{tb}}} \]
4. Kiểm tra lại kết quả:

   Sau khi tính toán, học sinh cần kiểm tra lại kết quả để đảm bảo đáp án chính xác, phù hợp với đơn vị đo lường.

Với phương pháp trên, học sinh có thể tự tin giải quyết các bài toán liên quan đến vận tốc trung bình một cách dễ dàng và chính xác.

• Vận tốc trung bình là gì?

Vận tốc trung bình là quãng đường mà một vật di chuyển được chia cho thời gian vật đó di chuyển. Công thức tính là \[ V_{\text{tb}} = \frac{S}{t} \], trong đó \(S\) là quãng đường và \(t\) là thời gian.

• Có thể áp dụng công thức tính vận tốc trung bình trong những trường hợp nào?

Công thức này có thể áp dụng trong các bài toán liên quan đến chuyển động đều, khi vật di chuyển với vận tốc không đổi hoặc khi tính trung bình cho các đoạn đường khác nhau.

• Vận tốc trung bình có giống vận tốc tức thời không?

Không. Vận tốc trung bình là trung bình của toàn bộ quãng đường, còn vận tốc tức thời là vận tốc tại một thời điểm cụ thể.

• Nếu có nhiều đoạn đường, làm sao để tính vận tốc trung bình?

Trong trường hợp có nhiều đoạn đường, ta tính tổng quãng đường và tổng thời gian để tìm vận tốc trung bình chung:

\[ V_{\text{tb}} = \frac{S_1 + S_2 + \dots + S_n}{t_1 + t_2 + \dots + t_n} \]
• Vận tốc trung bình có thể âm không?

Không. Vận tốc trung bình luôn là số dương vì quãng đường và thời gian đều là các đại lượng dương.

Vận tốc trung bình là một khái niệm quan trọng trong toán học lớp 5, không chỉ giúp các em học sinh hiểu rõ hơn về mối quan hệ giữa quãng đường, thời gian và vận tốc, mà còn giúp các em vận dụng kiến thức vào các tình huống thực tế trong cuộc sống. Qua các bài học và bài tập, học sinh đã được làm quen với công thức tính vận tốc trung bình:

\[
v = \frac{s}{t}
\]

• Trong đó:
  • \(v\) là vận tốc trung bình
  • \(s\) là quãng đường
  • \(t\) là thời gian

Thông qua các ví dụ và bài tập thực hành, các em học sinh đã nắm vững cách áp dụng công thức để giải quyết các vấn đề thực tế như tính vận tốc khi biết quãng đường và thời gian, hoặc xác định quãng đường và thời gian khi biết vận tốc. Những kiến thức này không chỉ giúp các em rèn luyện khả năng tính toán mà còn mở rộng tầm hiểu biết về các hiện tượng chuyển động trong tự nhiên và cuộc sống hàng ngày.

7.1. Tổng Kết Lý Thuyết

Vận tốc trung bình được tính bằng cách chia tổng quãng đường di chuyển được cho tổng thời gian di chuyển. Điều này có thể được áp dụng trong nhiều trường hợp khác nhau, từ chuyển động thẳng đều đến chuyển động không đều. Ngoài ra, khi giải bài toán vận tốc trung bình, học sinh cũng học cách đổi đơn vị đo để đảm bảo các giá trị đầu vào đồng nhất với nhau, điều này giúp tăng cường kỹ năng xử lý số liệu.

7.2. Tầm Quan Trọng Của Việc Hiểu Rõ Vận Tốc Trung Bình

Hiểu biết về vận tốc trung bình không chỉ giúp học sinh giải quyết các bài toán trong sách giáo khoa mà còn có ý nghĩa thực tiễn lớn. Các kiến thức này giúp các em hiểu rõ hơn về tốc độ di chuyển của các phương tiện giao thông, thời gian cần thiết để di chuyển giữa các địa điểm và các bài toán thực tế khác. Bằng việc nắm vững lý thuyết và thực hành qua các dạng bài tập, các em có thể ứng dụng tốt kiến thức vào cuộc sống, từ đó phát triển tư duy logic và kỹ năng giải quyết vấn đề một cách hiệu quả.

Việc rèn luyện thường xuyên và áp dụng kiến thức về vận tốc trung bình vào các bài toán sẽ giúp học sinh tự tin hơn trong các kỳ thi, đồng thời nâng cao khả năng tư duy và phân tích. Đây là nền tảng quan trọng không chỉ trong toán học mà còn trong nhiều lĩnh vực khác của cuộc sống.